φυσική    Γ' ΛΥΚΕΙΟΥ

ΘEΜΑ Β.

Tο σώμα Β του σχήματος είναι ακίνητο πάνω σε λείο οριζόντιο δάπεδο και δεμένο στην άκρη ιδανικού ελατηρίου. Το σώμα Α, μάζας  m_A , κινούμενο με ταχύτητα υ_Α=3m/s  κατά μήκος του άξονα του ελατηρίου, συγκρούεται κεντρικά με το σώμα Β τη χρονική στιγμή  t=0.  Οι αλγεβρικές τιμές των ταχυτήτων των σωμάτων μετά την κρούση (θετική φορά προς τα αριστερά) φαίνονται στο διάγραμμα ταχυτήτων-χρόνου.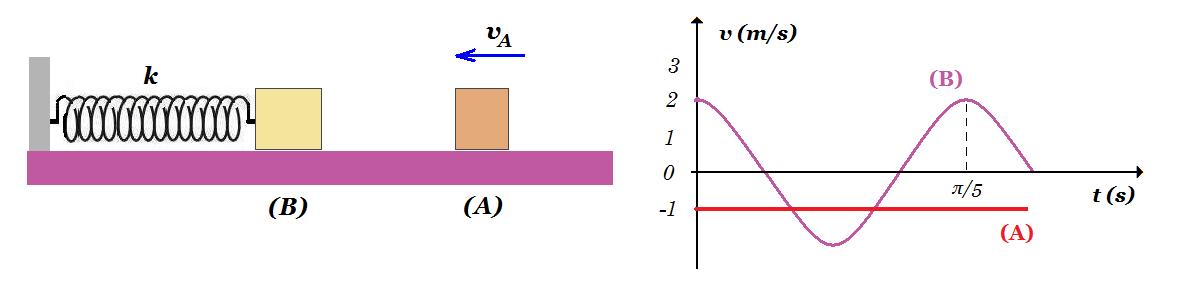

Η κρούση των σωμάτων είναι :    α)  πλαστική           β)  ελαστική          γ)  ανελαστική         

Να επιλέξετε τη σωστή απάντηση.                                   μονάδες 5
Να δικαιολογήσετε την επιλογή σας.                               μονάδες 10

Β.   ΛΥΣΗ

  διατήρηση ορμής m_A 3m/s = m_A (-1m/s)  + m_B 2m/s => 2m_A = m_B ,  

K_αρχ = ½ m_A (3m/s)² = 9/2 m_A ,  Κ_τελ = ½ m_A (-1m/s)² + ½ m_Β (2m/s)² = ½ m_A  + ½ 2m_Α 4 = 9/2 m_A   άρα Κ_αρχ = Κ_τελ  ελαστική κρούση   (β) 

ΘEΜΑ Γ.

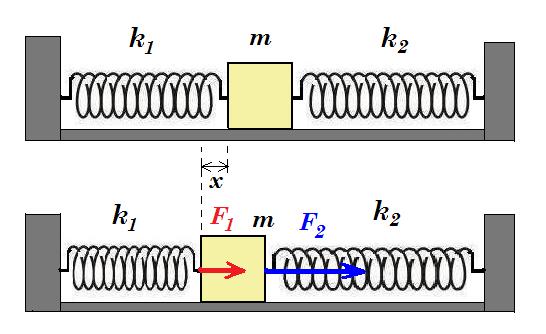Κάθε ελατήριο στο σχήμα  έχει το ένα άκρο του στερεωμένο σε ακίνητο σημείο και το άλλο του άκρο προσδεμένο στο σώμα μάζας m = 2 kg. Οι σταθερές των δύο ελατηρίων είναι k₁ = 80 N/m  και  k₂ = 120 N/m.  Το σώμα ισορροπεί και μπορεί να κινείται πάνω σε λείο οριζόντιο επίπεδο.  Αρχικά τα ελατήρια έχουν το φυσικό τους μήκος και οι άξονες τους βρίσκονται πάνω στην ίδια ευθεία.  Απομακρύνουμε το σώμα από τη θέση ισορροπίας του κατά την διεύθυνση του άξονα των ελατηρίων κατά x₀=0,1m προς τα δεξιά (θετική κατεύθυνση) δεν υπάρχουν τριβές ούτε αντίσταση αέρα.

Γ1.  Μελετήστε την κίνηση του σώματος.            μονάδες 10

Γ2.  Εκφράστε την κινητική ενέργεια του σώματος συναρτήσει του χρόνου και να κάνετε την γραφική παράσταση.      μονάδες 10

Γ3.  Εκφράστε την δυναμική ενέργεια του ελατηρίου (1) συναρτήσει της απομάκρυνσης x  του σώματος από την θέση ισορροπίας του και να κάνετε την γραφική παράσταση.   μονάδες 10

Γ4.  Εκφράστε τον ρυθμό μεταβολής της κινητικής ενέργειας του σώματος συναρτήσει του χρόνου και να κάνετε την γραφική παράσταση.         μονάδες 10

Γ5.  Ποιες χρονικές στιγμές η κινητική ενέργεια του σώματος  ισούται  με την δυναμική ενέργεια της ταλάντωσής του ;                      μονάδες 5

                    ΛΥΣΗ

Γ1.     μετακινούμε το σώμα κατά  x  από τη θέση ισορροπίας του 

 ΣF = F₁ + F₂ =  - k₁ x  +  (- k₂ x)  =  - (k₁ + k₂) x   η συνισταμένη δύναμη είναι ανάλογη της απομάκρυνσης   αυτό σημαίνει ότι το σώμα θα εκτελάσει Απλή Αρμονική Ταλάντωση  με σταθερά  D = k₁ + k₂ =  80 N/m + 120 N/m = 200 N/m    

η κυκλική συχνότητα της ταλάντωσης του σώματος είναι  ω² = D/m = 200 N/m / 2 kg = 100 => ω=10 rad/s 

η συχνότητα της ταλάντωσης του σώματος είναι   f = ω/2π = 10/2π Hz = 5/π Hz    

ο χρόνος περιόδου της ταλάντωσης του σώματος είναι  Τ = 2π/ω  = 2π/10 s = 0,2π s   

Αρχικά το σύστημα είναι σε ισορροπία  τη στιγμή t₀ = 0  μετακινούμε το σώμα  κατά x₀ = 0,1 m  προς τα δεξιά θετική κατεύθυνση  και το αφήνουμε ελεύθερο να κινηθεί.   Το σώμα θα εκτελάσει Απλή Αρμονική Ταλάντωση  με σταθερά  D = k₁ + k₂ = 200 N/m    το πλάτος της ταλάντωσής του θα είναι  Α = 0,1 m

η εξίσωση της απομάκρυσης από τη θέση ισορροπίας συναρτήσει του χρόνου είναι :

  x(t) = A ημ(ωt + φ) = 0,1 ημ(10t + π/2) = 0,1 συν10t           ημ(π/2) = +1   συν(π/2) = 0

διότι  την στιγμή  t = 0  είναι  x(0) = + 0,1 m  =>  0,1 ημ(10t + π/2) = +0,1 =>

                           =>   ημ(10t + π/2) = +1 = ημ(π/2)  =>  φ = π/2 rad = 90°   

η εξίσωση της ταχύτητας του σώματος συναρτήσει του χρόνου είναι :

    υ(t) = ωA συν(ωt + φ) =  1 συν(10t + π/2) = -1 ημ10t

η εξίσωση της επιτάχυνσης του σώματος συναρτήσει του χρόνου είναι :

    α(t) = - ω²A ημ(ωt + φ) = - 10 ημ(10t + π/2) = -10 συν10t

η δύναμη επαναφοράς συναρτήσει του χρόνου είναι :

ΣF = m a(t) = 2 { - 10 ημ(10t + π/2) } =>  ΣF(t) = - 20 ημ(10t + π/2) = -20 συν10t

κατά την διάρκεια της ταλάντωσής του το σώμα δέχεται δυνάμεις από τα ελατήρια,  αν μετατοπίζεται από τη Θ.Ι.  προς τα δεξιά  ( x>0 )   οι δυνάμεις από τα ελατήρια έχουν κατεύθυνση προς τα αριστερά   ενώ αν μετατοπίζεται από τη Θ.Ι.  προς τα αριστερά  ( x<0 )   οι δυνάμεις από τα ελατήρια έχουν κατεύθυνση προς τα δεξιά  

η δύναμη από το ελατήριο (1)  έχει εξίσωση :

F₁ = - k₁ x =>  F₁(t) = - 80  0,1 ημ(10t + π/2) =>  F₁(t) =  -8 ημ(10t + π/2)        F₁(0) = -8 ημ(π/2) = -8Ν 

η δύναμη από το ελατήριο (2)  έχει εξίσωση :

F₂ = - k₂ x =>  F₂(t) = - 120  0,1 ημ(10t + π/2) => F₂(t) = -12 ημ(10t + π/2)     F₂(0) = -12 ημ(π/2) = -12Ν

Γ2.    η κινητική ενέργεια του σώματος είναι :

Κ = ½ m υ²  = ½  2 { 1 συν(10t + π/2) }² = 1 συν²(10t + π/2) = 1 ημ²10t = ( 1 - συν20t ) / 2  = ½ - ½ συν20t                                                               συν2α  =  συν²α  -  ημ²α  =  1  -  2ημ²α  =  2συν²α  -  1

η δυναμική ενέργεια ταλάντωσης του σώματος είναι :

 U = ½ D x²  = ½  200  { 0,1 ημ(10t + π/2) }²  =>  U(t) = 1 ημ²(10t + π/2)  =  1 συν²10t  = ( 1 + συν20t ) / 2 =  ½ + ½ συν20t

η μηχανική ενέργεια ταλάντωσης του σώματος είναι :

 Ε = Κ + U = συν²(10t + π/2) + ημ²(10t + π/2) = 1 Joule  

Γ3.    η δυναμική ενέργεια του ελατηρίου (1)  είναι :

U_ελατ,1 = ½ k₁ x² = ½  80  x² =  40 x²    όπου   - 0,1 m £ x £ + 0,1 m 

ή  U_ελατ,1 = 40 { 0,1 ημ(10t + π/2) }² = 0,4 ημ²(10t + π/2) = 0,4 συν²10t  = 0,4 ( 1 + συν20t ) / 2  =  0,2 + 0,2 συν20t

η δυναμική ενέργεια του ελατηρίου (2)  είναι :

U_ελατ,2 = ½ k₂ x²  = ½ 120 { 0,1 ημ(10t + π/2) }² = 0,6 ημ²(10t + π/2) = 0,6 συν²10t  = 0,6 ( 1 + συν20t ) / 2  =  0,3 + 0,3 συν20t

η ολική δυναμική ενέργεια των ελατηρίων είναι :

U_ελατ,1 + U_ελατ,2 = 0,4 ημ²(10t + π/2) + 0,6 ημ²(10t + π/2) =  ημ²(10t + π/2)  

Γ4.    ο ρυθμός μεταβολής της κινητικής ενέργειας του σώματος είναι :  

dΚ/dt = m υ dυ/dt = m υ(t) a(t) => dK/dt = 2 1 συν(10t+π/2) {- 10 ημ(10t+π/2) } = - 20 ημ(10t+π/2) συν(10t+π/2) 

  ή   dK/dt  =  - 10 ημ(20t + π) = + 10 ημ20.t                ημ2α  =  2 ημα συνα  

ο ρυθμός μεταβολής της δυναμικής ενέργειας της ταλάντωσης του σώματος είναι :

dU/dt = D x dx/dt  = D x(t) υ(t) = 200  0,1 ημ(10t + π/2)  1 συν(10t + π/2) = 20 ημ(10t + π/2) συν(10t + π/2)

ή   dU/dt  = 10 ημ(20t + π) = - 10 ημ20.t                      ημ2α  =  2 ημα συνα  

επειδή η μηχανική ενέργεια της ταλάντωσης του σώματος είναι σταθερή (δεν υπάρχουν τριβές ούτε αντίσταση αέρα)  Ε = 0 => K + U = 0  =>  dK/dt + dU/dt = 0  => dK/dt = - dU/dt  

για την δυναμική ενέργεια της ταλάντωσης  και  την κινητική ενέργεια του σώματος  ο χρόνος περιόδου είναι :  Τ = 2π/ω  =  2π / 20  =  π/10 s   και όχι  2π/10 s  = π/5 s     

 Γ5.   Ποιες χρονικές στιγμές η κινητική ενέργεια του σώματος  ισούται  με την δυναμική ενέργεια της ταλάντωσής του ; 

 K = U  =>  συν²(10t + π/2) = ημ²(10t + π/2)  =>  εφ²(10t + π/2) = 1  =>

      =>  εφ(10t + π/2) = ±1  =>  φ = 10t + π/2  =  Ν π/2 + π/4       

      =>   t  =  Ν π/20  -  π/40     Ν = 1, 2, 3, ...

Ν=1    t = π/20 - π/40 = π/40 s            

Ν=2    t = 2 π/20 - π/40 = 3π/40 s

Ν=3   t = 3 π/20 - π/40 = 5π/40 s       

Ν=4    t = 4 π/20 - π/40 = 7π/40 s

φυσική    Γ' ΛΥΚΕΙΟΥ

ΘEΜΑ Δ. 

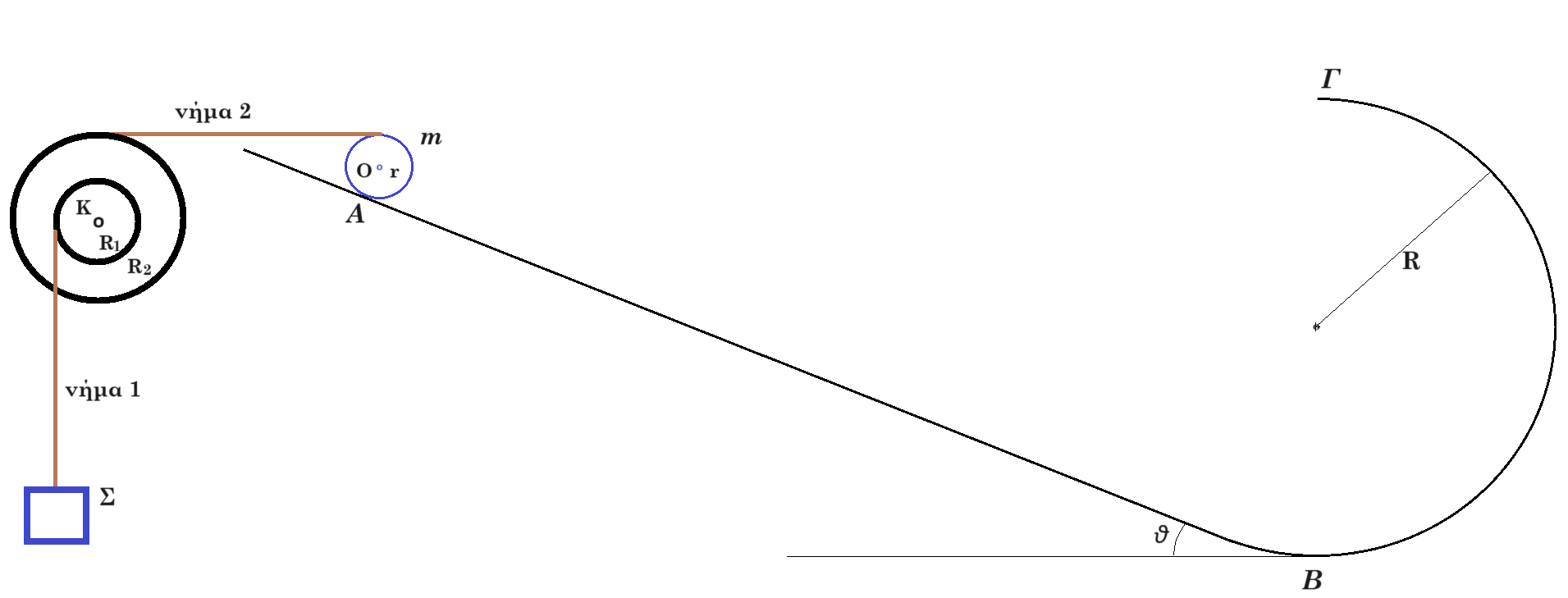
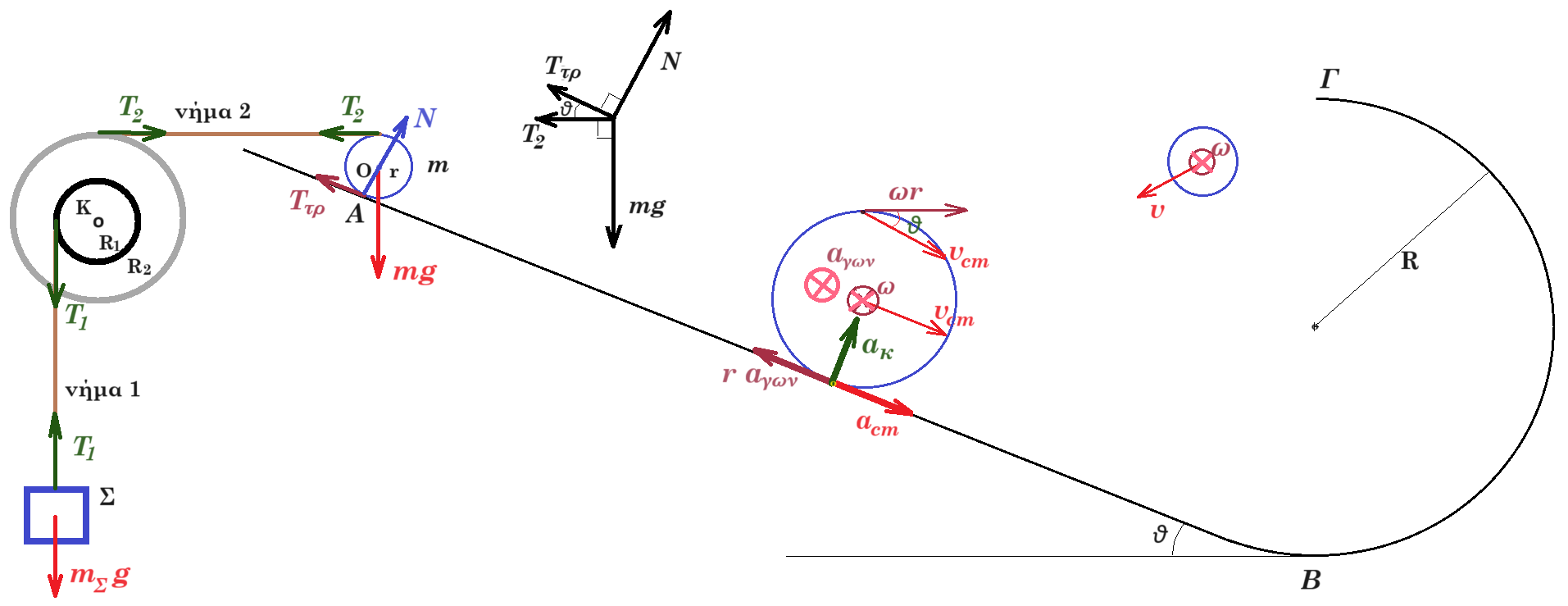
Θεωρούμε την διάταξη του σχήματος, σε κατάσταση ισορροπίας, σε κατακόρυφο επίπεδο.  Στη θέση Α του κεκλιμένου επιπέδου ισορροπεί κυκλική στεφάνη μάζας m = 3kg ακτίνας r = 0,1m.  Το κεκλιμένο επίπεδο γωνίας κλίσεως θ, ( ημθ = 0,6  συνθ = 0,8 ) στην βάση του συνδέεται με κατακόρυφο ημικύκλιο ακτίνας R = 1m.  Η στεφάνη στο άνω της άκρο συνδέεται με οριζόντιο αβαρές μη εκτατό νήμα 2 (σταθερού μήκους) με τροχαλία μάζας Μ=5kg   εσωτερικής ακτίνας R₁ = 0,2m   εξωτερικής ακτίνας R₂ = 0,5m.  Η τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από άξονα που διέρχεται από το κέντρο της Κ ( σταθερό ακίνητο σημείο )  και είναι κάθετος στο επίπεδο της. Γύρω από την τροχαλία έχουμε τυλίξει αρκετές φορές αβαρές μη εκτατό νήμα 1  το οποίο συνδέεται με σώμα Σ.  

Δ1.   Βρείτε την μάζα του σώματος Σ.                                μονάδες 12

Κάποια στιγμή ( t₀=0 ) αφαιρούμε το νήμα 2,  οπότε η στεφάνη κατέρχεται επί του κεκλιμένου επιπέδου κυλιόμενη ( δεν ολισθαίνει )  ενώ το σώμα Σ  κινείται κατακόρυφα προς τα κάτω  και η τροχαλία περιστρέφεται γύρω από τον άξονά της χωρίς τριβές έχοντας γωνιακή επιτάχυνση  α_γων = 10/3 m/s².  

Δ2.  Εάν η μάζα του σώματος Σ είναι m_Σ = 2,5 kg  εκφράστε την στροφορμή του συναρτήσει του χρόνου.           μονάδες 8

Δ3.  Τη χρονική στιγμή t₀ = 0  η στεφάνη αρχίζει να κατέρχεται κυλιόμενη επάνω στο κεκλιμένο επιπέδο  ενώ το κέντρο της έχει επιτάχυνση  α_cm = 3 m/s².  Τη χρονική στιγμή t₁=1s  βρείτε την ταχύτητα του ανώτερου σημείου της στεφάνης   καθώς  και την επιτάχυνση του σημείου επαφής της στεφάνης με το κεκλιμένο επίπεδο.                 μονάδες 10    

Δ4.  Η στεφάνη κυλίεται (δεν ολισθαίνει) κινούμενη στο κεκλιμένο επίπεδο,  ανέρχεται κυλιόμενη στο ημικύκλιο  και διέρχεται από την ανώτατη θέση Γ του ημικυκλίου έχοντας ταχύτητα μέτρου  3m/s.   Βρείτε την δύναμη που δέχεται από το ημικύκλιο στο σημείο Γ  και  την γωνιακή ταχύτητάς της ( διεύθυνση, φορά, μέτρο )  μετά από  0,2 sec  αφού περάσει το σημείο Γ.          μονάδες 10    

   επιτάχυνση βαρύτητας  g = 10 m/s²     

                     ΛΥΣΗ

Δ1.   ισορροπία  Σ :  Τ₁  =  m_Σ g     (1)  

 ισορροπία τροχαλίας :   Στ_(Κ)  =  0  =>  Τ₂ R₂  -  T₁ R₁  =  0  =>  T₂  0,5  =  T₁  0,2  => 

                                                       =>   T₂  =  0,4 T₁   =  0,4 m_Σ g  =>  Τ₂ = 4 m_Σ     (2)              

ισορροπία στεφάνης :   Στ_(Ο)  =  0  =>  Τ₂ r  -  Τ_τρ r  =  0  =>  Τ₂ = Τ_τρ    (3)    

ΣF_x = 0  =>   N ημθ  -  Τ₂  -  Τ_τρ συνθ  =  0  =>⁽³⁾  N ημθ  -  Τ₂  -  Τ₂ συνθ  =  0  =>  

              =>  N 0,6  -  Τ₂  -  Τ₂ 0,8  =  0  =>  Ν  =  3 Τ₂     (4)   

ΣF_y = 0  =>  N συνθ  -  m g  +  Τ_τρ ημθ  =  0  =>  3Τ₂  0,8  -  3 10  +  Τ₂  0,6  =  0   =>  Τ₂ = 10 Ν

                     άρα  η (2) =>  Τ₂ = 4 m_Σ  =>  10  = 4 m_Σ  =>  m_Σ = 2,5 kg 

Δ2.   επιτάχυνση σώματος Σ :  a_Σ = α_γων R₁  =  10/3 rad/s²  0,2 m  =  2/3 m/s²   

  ταχύτητα σώματος Σ :   v_Σ  =  a_Σ t  =  2/3 t       

στροφορμή του σώματος Σ  ως προς το σημείο Κ :   L  =  m_Σ  v_Σ R₁  =  2,5   2/3 t  0,2  =>   L(t)  =  t/3   

Δ3.   a_cm = α_γων r  =>  3 m/s²  = α_γων  0,1 m  =>  a_γων = 30 rad/s²       ω = α_γων t = 30 rad/s² 1 s = 30 rad/s    

           υ_cm = = ω r = 30 rad/s  0,1 m = 3 m/s  

  υ²  =  υ_cm²  +  (ω r)²  +  2 υ_cm  ω r  συνθ  =  2 υ_cm² ( 1 + συνθ ) = 2 3²  (1 + 0,8 ) =  18  1,8 =  81  0,4  =>  υ = 9√0,4 m/s    

α_γων = M.g.ημθ / (Ι/R² + Μ).R  =>  α_γων = M.g.ημθ / ( Μ + Μ).R   =>  α_γων = M.g.ημθ / 2Μ.R   => 

       =>   α_γων =  g.ημθ / 2R   =>  α_γων = 10 0,6 / 2 0,1  =>  α_γων =  30 rad/s²

στο σημείο Ε  η στεφάνη  έχει  τρεις επιταχύνσεις  την επιτάχυνση του κέντρου μάζας ,  την γωνιακή  και  την  κεντρομόλο    αλλά  η επιτάχυνση του κέντρου μάζας  και η γωνιακή είναι αντίθετες και έχουν συνισταμένη μηδέν  ενώ   η κεντρομόλος ισούται με  α_κ  =  υ² / r  =  ω² r  =  30²  0,1  =  90 m/s²    

Δ4.  όταν η στεφάνη διέρχεται από την ανώτερη θέση Γ υ_Γ = 3 m/s :  ΣF_y = F_κ  =>  mg  + Ν = m v_Γ²/(R - r)  =>   30  + Ν =  3  3² / (1 - 0,1)  =>  Ν  =  27/0,9 - 30 = 0    άρα  μόλις διέρχεται από την ανώτερη θέση Γ του ημικυκλίου  διότι ισχύει Ν = 0  

η στεφάνη στον αέρα δεν δέχεται δύναμη που να δημιουργεί ροπή  συνεπώς  η γωνιακή ταχύτητά της είναι σταθερή  ω = υ_Γ / r = 3 m/s  /  0,1 m  = 30 rad/s