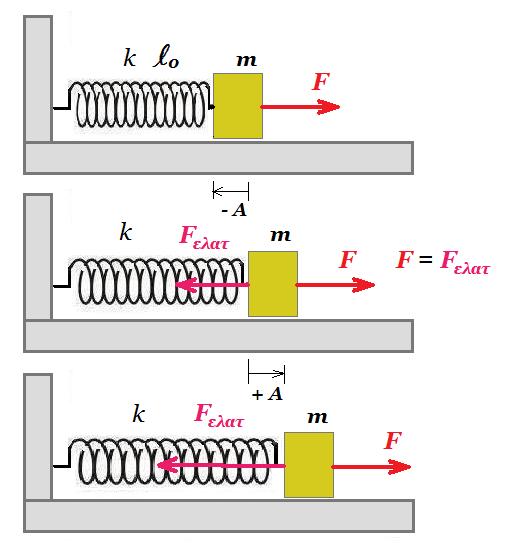
Ένα σώμα ισορροπεί στο κάτω άκρο ενός κατακόρυφου ιδανικού ελατηρίου, σταθερά k, το οποίο κρέμεται από το ταβάνι, επιμηκύνοντάς το κατά d. Εκτρέπουμε το σώμα κατακόρυφα προς τα κάτω κατά 2d και σε μια στιγμή t=0, το αφήνουμε να ταλαντωθεί. Με δεδομένο ότι η προς τα πάνω κατεύθυνση θεωρείται θετική, να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές ή λανθασμένες, δίνοντας σύντομες δικαιολογήσεις.

i)   Η μέγιστη δυναμική ενέργεια ταλάντωσης είναι ίση με 2kd².

Σε μια στιγμή t₁, όπου 3Τ/4 < t₁ < Τ το ελατήριο έχει επιμήκυνση Δl=2d. Για τη στιγμή αυτή:

ii)  Οι αλγεβρικές τιμές ταχύτητας και επιτάχυνσης είναι αρνητικές.

iii) Η δυναμική ενέργεια ταλάντωσης είναι ίση με U₁=2kd².

iv) Η κινητική ενέργεια του σώματος είναι ίση με Κ₁=1,5 kd².

v)  Η μέγιστη δυναμική ενέργεια του ελατηρίου είναι ίση με U_mαx=4,5 kd².

 ΑΣΚΗΣΗ  9 

Το σώμα Σ μάζας   m = 1 kg  του σχήματος είναι δεμένο στο ένα άκρο οριζοντίου ελατηρίου σταθεράς   k = 400 N/m.  Το άλλο άκρο του ελατηρίου είναι ακλόνητα στερεωμένο.  Το σύστημα ελατήριο – σώμα Σ ισορροπεί σε λείο οριζόντιο επίπεδο.  Τη χρονική στιγμή  t₀=0  ασκείται στο σώμα Σ σταθερή οριζόντια δύναμη μέτρου  F  με αποτέλεσμα το σύστημα να ξεκινήσει απλή αρμονική ταλάντωση πλάτους  A = 0,4 m.

Να βρεθεί:
α)  το μέτρο F  της δύναμης,
β)  η εξίσωση  x = f(t)  της απομάκρυνσης του σώματος από τη θέση ισορροπίας,
γ)  η εξίσωση   F_ελατ = f(t)   της δύναμης που ασκεί το ελατήριο στο σώμα.
δ)  Το πλάτος   Α'   και η ολική ενέργεια  Ε'  της νέας ταλάντωσης που θα εκτελέσει το σώμα, αν κάποια στιγμή που το σώμα βρίσκεται στην ακραία θετική θέση ταλάντωσης, καταργηθεί η δύναμη  F.

 

 Θέμα 1 

Το σώμα Σ μάζας m₁ = 2 kg  ισορροπεί  στο άκρο ελατηρίου  πάνω στο κεκλιμένο επίπεδο (θ = 30°). Το ελατήριο έχει επιμήκυνση Δl = 0,05 m.  Απομακρύνουμε το σώμα προς τα κάτω επί του επιπέδου κατά 0,1m  και το αφήνουμε ελέυθερο να εκτελέσει Α.Α.Τ.  Όταν φθάνει στην ανώτερη θέση ταλάντωσης συσσωματώνεται με κινούμενο σώμα μάζας  m₂ = 4 kg  που κινείται οριζόντια με σταθερή ταχύτητα  υ₀ = √3 m/s.  Θετική φορά προς τα δεξιά.

  χ = 2d ημ(ωt + 3π/2)              υ = 2dω συν(ωt + 3π/2)           α = - 2dω² ημ(ωt + 3π/2)  

   U_max =  ½ k (2d)²  =  2kd² =  E   ενέργεια ταλάντωσης                    

  v < 0          a > 0              U₁ = ½ k d²        K₁ =  Ε  -  U₁  =  2 k d²  -  ½ k d²  =  1,5 k d²        

       U_{ελατ.,max} =  ½ k (d + 2d)²  =  4.5 k d²     

Θέμα 1

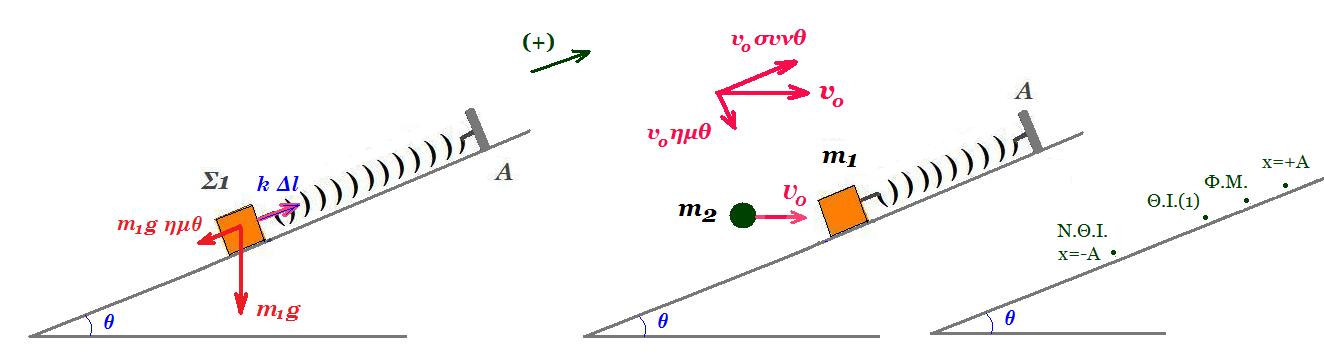
ισορροπία σώματος (1):  m₁ g ημ30° = k Δl  => 2  10  ½ =  k  0,05  =>  k = 10 / 0,05 = 200 N/m 

   k = m₁  ω²  =>  200 = 2  ω²  =>  ω = 10 rad/s       T = 2π/ω = π/5 s         f = 1/T = 5/π Hz

   x(t) = 0,1 ημ(10t + 3π/2)         υ(t) = 1 συν(10t + 3π/2)              α(t) = - 10 ημ(10t + 3π/2)

  ΣF  =  m₁ a  = - 20 ημ(10t + 3π/2)

  ΣF  =  m₁ a  =>   - m₁ g ημ30°  +  F_ελατ  =  m₁ a  =>    F_ελατ  =  m₁ g ημ30°  + m₁ a  =>   

        =>    F_ελατ  =   2  10  ½  - 20 ημ(10t + 3π/2)  =>     F_ελατ(t) =  10 - 20 ημ(10t + 3π/2) 

 F_ελατ(0)  =  10 - 20 ημ(3π/2)  =  10 - 20 (-1) = 30 Ν  =  200 N/m  0,15 m  =

               = - 200 N/m  ( - 0,1 m - 0,05 m ) =  - k ( x + Δl )   

   διότι    x = - 0,1 m = - A    και  Δl = - 0,05 m

 διατήρηση ορμής για την κρούση :

    m₂ υ₀ συν30°  = (m₁ + m₂) υ  =>   4 3^½  3^½/2  = (2 + 4) υ  =>  υ = 1 m/s

το συσσωμάτωμα αμέσως μετά την κρούση έχει ταχύτητα με μέτρο 1 m/s  και κατεύθυνση προς το άνω μέρος του κεκλιμένου επιπέδου,   

τη στιγμή της κρούσης το σώμα (1) είναι στο άνω άκρο της ταλάντωσής του  δηλαδή  x = +0,1 m   οπότε το ελατήριο έχει  συσπείρωση   x - Δl  =  0,1 m - 0,05 m = 0,05 m

ισορροπία συσσωματώματος :  ( m₁ + m₂ ) g ημ30° = k Δl'  =>  6  10  ½ =  200  Δl'  => Δl' = 0,15m

  για την ταλάντωση του συσσωματώματος :  ½ (m₁ + m₂) υ²  +  ½ k (Δl' + Δl)²  =  ½ k Α' ²  =>  

      =>    ½  6  1²  +  ½  200  (0,15 + 0,05)²  =  ½  200  Α' ²  =>

      =>    3  +  100  0,04  =  100  Α' ²  =>     Α' = √7/10 m 

 k = ( m₁ + m₂ ) ω' ²  =>  200 = 6 ω² => ω = 10 / √3 rad/s              T = 2π/ω = π√3/5 s      

 x(t) = 0,1 √7 ημ(10/√3 t + φ)       υ(t) = √(7/3) συν(10/√3 t + φ)      α(t) = - 10 √7/3  ημ(10/√3 t + φ)  

αμέσως μετά την κρούση το συσσωμάτωμα βρίσκεται σε απομάκρυνση + 0,2 m  και έχει ταχύτητα +1 m/s

 x(0) = 0,1 √7 ημφ = + 0,2 m =>  ημφ = +2/√7                       συνφ =  ± √ ( 1 - 4/7 ) = ± √ (3/7)

 υ(0) = √(7/3) συνφ = +1 m/s => συνφ = +√(3/7)

.................................................................................................................

άλλος τρόπος :

αρχικά  το ελατήριο είναι συσπειρωμένο κατά  0,05m  και   το συσσωμάτωμα αμέσως μετά την κρούση έχει ταχύτητα με μέτρο 1 m/s  και κατεύθυνση προς το άνω μέρος του κεκλιμένου επιπέδου,

έστω ανεβαίνει κατά  x  επί του κεκλιμένου  οπότε ακινητοποιείται στιγμιαία,  τότε το ελατήριο είναι συσπειρωμένο κατά    x + 0,05

½ (m₁ + m₂) υ²  +   ½ k  0,05²  =  (m₁ + m₂) g  x ημ30°  +   ½ k  (x + 0,05)²   =>  

½  6  1²  +   ½  200  0,05²  =  6  10  x ½  +   ½  200  ( x² + 0,05² + 2 x 0,05 )   =>  

  3   =  30  x   +   100 x²  +  10 x   =>    100 x²  +  40 x  -  3    

  Δ = 1600 + 1200 = 2800  = 20 √7

 x  =  ( - 40 ± 20 √7  ) / 200  =  - 0,2 ± √7/10   δεκτή λύση :    x  = - 0,2 + √7/10  >  0

το πλάτος της ταλάντωσης του συσσωματώματος θα είναι :  Α' =  Δl' +( x + 0,05 )    =  0,15 + ( - 0,2 + √7/10 ) + 0,05 = 0,1√7 m = Α'

 ΑΣΚΗΣΗ  9 

Για τη νέα ολική ενέργεια της ταλάντωσης έχουμε :  Ε' = ½ . k . (A')² = ½ . 400 N/m . 0,8² m² =>  E' = 128 J   

        W_F =  F A = 160 N  0,4 m  =  64 J     U  = 0,5 k A²  =  0,5  400  0,4²  =  200  0,16  =  32 J        K =  0,5 m v²  =  0,5  1  8²  =  32 J  

        W_F =  F 2A = 160 N  0,8 m  =  128 J     U  = 0,5 k (2A)²  =  0,5  400  0,8²  =  200  0,64  =  128 J        K =  0 J  

  x(t)  =  +0,2m  =  0,4 . ημ(20.t + 3π/2) =>   ημ(20.t + 3π/2)  =  +0,5    =>   συν²(20.t + 3π/2) = 3/4             v²  =  8² . συν²(20.t + 3π/2)  =  64  3/4  =  48

        W_F =  F  = 160 N  0,6 m  =  96 J       U  = 0,5 k x²  =  0,5  400  0,6²  =  200  0,36  =  72 J         K =  0,5 m v²  =  0,5  1  48  =  24 J