Ροπή δύναμης - Α.Α.Τ. σώματος

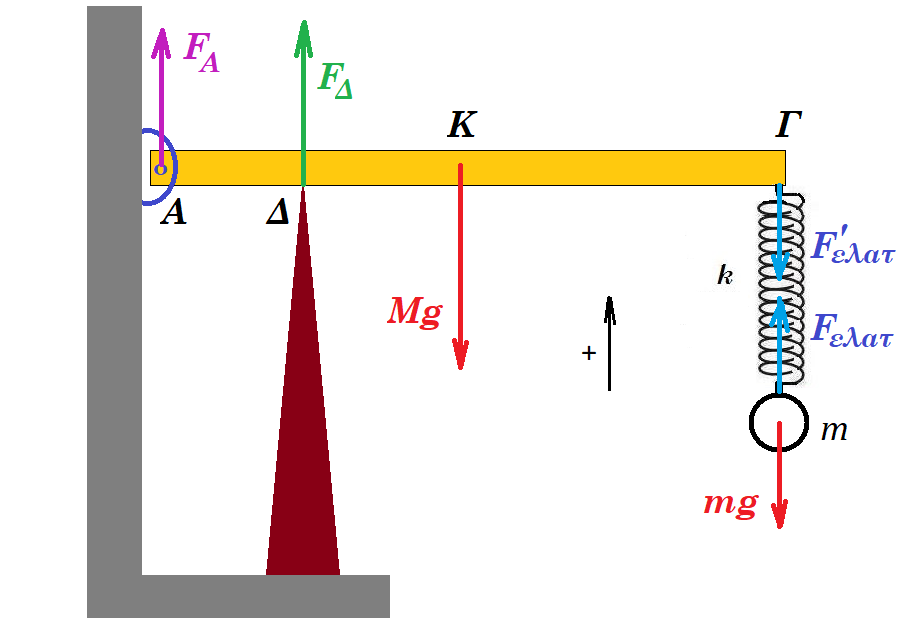
Στο σχήμα η ομογενής ράβδος ΑΓ έχει μήκος ΑΓ = ℓ μάζα Μ = 4 Kg και συνδέεται με άρθρωση σε τοίχο με το άκρο της Α. Στο σημείο Δ, με ΑΔ = ℓ/4 υπάρχει υποστήριγμα και στο άκρο Γ είναι στερεωμένο το πάνω άκρο ιδανικού ελατηρίου σταθεράς k = 100 Ν/m, στο κάτω άκρο του οποίου έχει συνδεθεί σφαιρίδιο (Σ) μάζας m = 1 Kg. Η ράβδος και το σφαιρίδιο ισορροπούν και η ράβδος είναι οριζόντια.

Α. Υπολογίστε τα μέτρα των δυνάμεων που ενεργούν στη ράβδο.

Β. Εκτρέπουμε το σφαιρίδιο κατακόρυφα προς τα πάνω κατά d = 0,2 m και στη συνέχεια το αφήνουμε ελεύθερο τη χρονική στιγμή t₀ = 0 οπότε αρχίζει να εκτελεί απλή αρμονική ταλάντωση.

Β1. Υπολογίστε την ενέργεια της ταλάντωσης

Β2. Γράψτε την εξίσωση απομάκρυνσης – χρόνου x(t)

Β3. Γράψτε την εξίσωση της δύναμης που ασκεί το ελατήριο στο σφαιρίδιο (Σ), σε συνάρτηση με το χρόνο.

Β4. Γράψτε την εξίσωση της δύναμης που ασκείται στη ράβδο στο σημείο της άρθρωσης, Α , σε συνάρτηση με την απομάκρυνση της α.α.τ. και παραστήστε την γραφικά.

Γ. Ποιο το μέγιστο πλάτος των ταλαντώσεων του συστήματος ελατήριο – σφαιρίδιο (Σ) με τη ράβδο να παραμένει ακίνητη;

Δ. Αν η σφαίρα ταλαντώνεται μέσα σε ρευστό σώμα οπότε δέχεται δύναμη F = - 0,2 υ όπου b = 0,2 kg/s είναι συντελεστής απόσβεσης.

Δ1. Βρείτε την εξίσωση απομάκρυνσης – χρόνου x(t) για την φθίνουσα ταλάντωση της σφαίρας.

Δ2. Αν τη στιγμή t=0 η σφαίρα έχει ενέργεια ταλάντωσης Ε₀ = 2 J βρείτε σε πόσο χρόνο η ενέργεια της ταλάντωσής της γίνεται 0,25 J.

Δίνεται g = 10 m/s² , σταθερά : Λ = b / 2m , ln2 = 0,7

(Α) ισορροπία σφαίρας : mg = F_ελατ => 10 Ν = 100 Ν/m x₀ => x₀ = 0,1m επιμήκυνση ελατηρίου όταν η σφαίρα ισορροπεί

η ράβδος δέχεται στο άκρο της Γ από το ελατήριο δύναμη F'_ελατ = - F_ελατ = - 10 Ν

ισορροπία ράβδου ΑΓ : ροπές ως προς Α : - Mg l/2 + F'_ελατ l + F_Δ l/4 = 0 =>

=> - 40 l/2 - 10 l + F_Δ l/4 = 0 => F_Δ = 120 Ν κατακόρυφη προς τα επάνω

ΣF_y = 0 => F_Δ + Mg + F'_ελατ + F_Α = 0 => + 120 - 40 - 10 + F_Α = 0 => F_Α = - 70 N

ροπές ως προς Δ : - Mg l/4 + F'_ελατ 3l/4 + F_Α (- l/4) = 0 => - 40 l/4 - 10 3l/4 - F_Α l/4 = 0 =>

=> - 40 - 30 - F_Α => F_Α = - 70 Ν κατακόρυφη προς τα κάτω

(Β) στην ισορροπία η επιμήκυνση του ελατηρίου είναι x₀ = 0,1 m

ω² = k / m = 100 / 1 => ω = 10 rad/s f = ω / 2π = 5/π Hz T = 1/f = π/5 s

E = ½ k d² = ½ 100 0,2² = 2 Joule ενέργεια της ταλάντωσης της σφαίρας

x(t) = 0,2 ημ(10t +π/2) x(0) = + 0,2 m v(t) = 2 συν(10t +π/2) α(t) = - 20 ημ(10t +π/2)

ΣF = mα => mg + F_ελατ = mα => - 10 + F_ελατ = - 20 ημ(10t +π/2) =>

=> F_ελατ = 10 - 20 ημ(10t +π/2) = 10 - 100x = - 100 (x - 0,1) - 0,2 m £ x £ + 0,2 m

άρα F'_ελατ = - 10 + 20 ημ(10t +π/2) = - 10 + 100x - 0,2 m £ x £ + 0,2 m

=> - 40 l/2 + {- 10 + 20 ημ(10t +π/2)} l + F_Δ l/4 = 0 => - 80 + 4 (- 10 + 20 ημ(10t +π/2) ) + F_Δ = 0 =>

=> F_Δ(t) = 120 - 80 ημ(10t +π/2) κατακόρυφη F_Δ(x) = 120 - 400 x - 0,2 m £ x £ + 0,2 m

ροπές ως προς Δ : - Mg l/4 + F'_ελατ 3l/4 + F_Α (- l/4) = 0 =>

=> - 40 l/4 + (- 10 + 20 ημ(10t +π/2) ) 3l/4 - F_Α l/4 = 0 => - 40 - 30 + 60 ημ(10t +π/2) - F_Α =>

=> F_Α(t) = - 70 + 60 ημ(10t +π/2) κατακόρυφη F_Α(x) = - 70 + 300 x - 0,2 m £ x £ + 0,2 m

δυναμική ενέργεια της σφαίρας κατά την ταλάντωση :

U = ½ k x² = ½ 100 [ 0,2 ημ(10t + π/2) ]² => U(t) =2 ημ²(10t + π/2) U(0) = 2 J

κινητική ενέργεια της σφαίρας κατά την ταλάντωση :

Κ = ½ m v² = ½ 1 [ 2 συν(10t + π/2) ]² => Κ(t) = 2 συν²(10t + π/2) K(0) = 0

ρυθμός μεταβολής της δυναμικής ενέργειας της σφαίρας κατά την ταλάντωση :

= 40 ημ(10t + π/2) συν(10t + π/2) => dU(t)/dt = 20 ημ(20t + π) = - 20 ημ20t

ρυθμός μεταβολής της κινητικής ενέργειας της σφαίρας κατά την ταλάντωση :

dΚ/dt = m v dv/dt = m v a = 1 2 συν(10t +π/2) [ -20 ημ(10t +π/2) ] =

= - 40 συν(10t + π/2) ημ(10t + π/2) => dΚ(t)/dt = - 20 ημ(20t + π) = 20 ημ20t

δυναμική ενέργεια του ελατηρίου κατά την ταλάντωση σε σχέση με την απομάκρυνση του σώματος από την θέση ισορροπίας του :

U_ελατ = ½ k (x + x₀)² => U_ελατ(x) = 50 (x - 0,1)² - 0,2 m £ x £ + 0,2 m

U_ελατ(- 0,2m) = 50 (-0,2-0,1)² = 4,5 J U_ελατ(- 0,1m) = 50 (-0,1-0,1)² = 2 J U_ελατ(0) = 50 (-0,1)² = 0,5 J

U_ελατ(+ 0,1m) = 50 (+ 0,1 - 0,1)² = 0 J U_ελατ(+ 0,2m) = 50 (+ 0,2 - 0,1)² = 0,5 J

δυναμική ενέργεια του ελατηρίου κατά την ταλάντωση σε σχέση με τον χρόνο :

U_ελατ(0) = 50 [ 0,2 ημ(π/2) - 0,1 ]² = 50 ( 0,2 - 0,1 )² = 0,5 J = U_ελατ(+ 0,2m) άνω άκρο ταλάντωσης σφαίρας

U_ελατ(π/20) = 50 [ 0,2 ημ(10 π/20 + π/2) - 0,1 ]² = 50 [ 0,2 ημ(π) - 0,1 ]² =

= 50 ( - 0,1 )² = 0,5 J = U_ελατ(0m) θέση ισορροπίας σφαίρας

U_ελατ(π/10) = 50 [ 0,2 ημ(10 π/10 + π/2) - 0,1 ]² = 50 [ 0,2 ημ(3π/2) - 0,1 ]² =

= 50 (- 0,2 - 0,1)² = 4,5 J = U_ελατ(-0,2m) κάτω άκρο ταλάντωσης σφαίρας

U_ελατ(3π/20) = 50 [ 0,2 ημ(10 3π/20 + π/2) - 0,1 ]² = 50 [ 0,2 ημ(2π) - 0,1 ]² =

= 50 (- 0,1)² = 0,5 J = U_ελατ(0m) θέση ισορροπίας σφαίρας

U_ελατ(π/5) = 50 [ 0,2 ημ(10 π/5 + π/2) - 0,1 ]² = 50 [ 0,2 ημ(π/2) - 0,1 ]² =

= 50 ( 0,2 - 0,1 )² = 0,5 J = U_ελατ(+0,2m) άνω άκρο ταλάντωσης σφαίρας

(Γ) F_Δ = 0 => 120 - 400 x = 0 => x = 120 / 400 = 0,3 m μέγιστο πλάτος ταλάντωσης

η ράβδος χάνει την επαφή της με το στήριγμα στο σημείο Δ όταν F_Δ = 0

Στ_(Α) = 0 => - Mg l/2 + F'_ελατ l + F_Δ l/4 = 0 => - 40 l/2 + (-10 + 100x) l = 0 =>

την στιγμή όπου x = + 0,3 m η σφαίρα είναι στην ανώτερη θέση της ταλάντωσής της

το ελατήριο είναι συσπειρωμένο κατά 0,2 m έχει δυναμική ενέργεια U_ελατ = ½ k (x+x₀)² = ½ 100 (0,3-0,1)² = 2 J

η ράβδος δέχεται δύναμη από το ελατήριο : F'_ελατ = - 10 + 100.x = - 10 + 100.(+0,3) = +20Ν κατακόρυφη προς τα πάνω

στην άρθρωση στο σημείο Α η ράβδος δέχεται δύναμη : F_Α = - 70 + 300.x = - 70 + 300.(+0,3) = +20Ν κατακόρυφη προς τα πάνω

(Δ) σταθερά Λ = b / 2m = 0,2 / 2 = 0,1 s^-1 ω² = (k / m)² - Λ² = 100² - 0,1² = 100² ω = 10 rad/s T = π/5 s

εξίσωση της απομάκρυνσης : x(t) = A₀ e^-Λt συνωt = 0,2 e^-0,1.t συν10t

ενέργεια ταλάντωσης σφαίρας : Ε(t) = Ε₀ e^-2.Λ.t => 0,25 = 2 e^-2.0,1.t => 1/8 = e^-2.0,1.t => 8 = e^t/5 => ln8 = t/5 => t = 5 ln8 = 5 ln2³ = 5 3 ln2 = 15 0,7 => t = 10,5 s