φυσική Γ' ΛΥΚΕΙΟΥ

ΘΕΜΑ Β1

Ομογενής δίσκος πολύ μικρού πάχους ακτίνας R=0,2m, εκτελεί στροφική κίνηση γύρω από σταθερό άξονα ο οποίος διέρχεται από το κέντρο του Κ και είναι κάθετος στο επίπεδό του.  H γωνιακή ταχύτητά του μεταβάλλεται συναρτήσει του χρόνου. Βρείτε τη γωνιακή μετατόπιση του δίσκου στο χρονικό διαστήμα [3s , 5s]. μονάδες 10

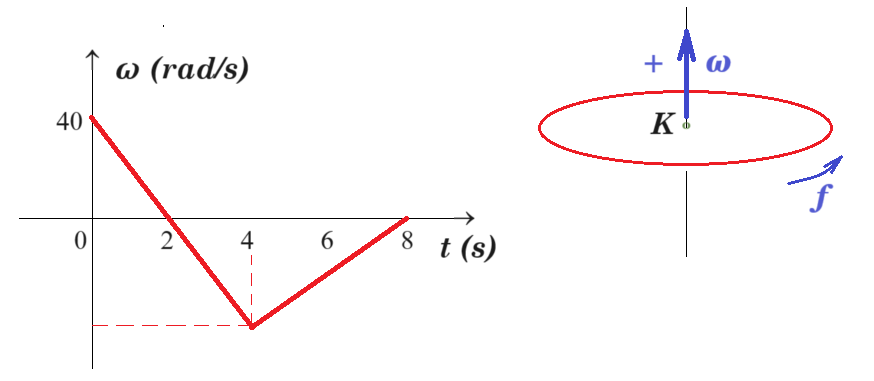
ΘΕΜΑ Β1     ΛΥΣΗ

Γράψτε τις εξισώσεις της γωνιακής ταχύτητας συναρτήσει του χρόνου.

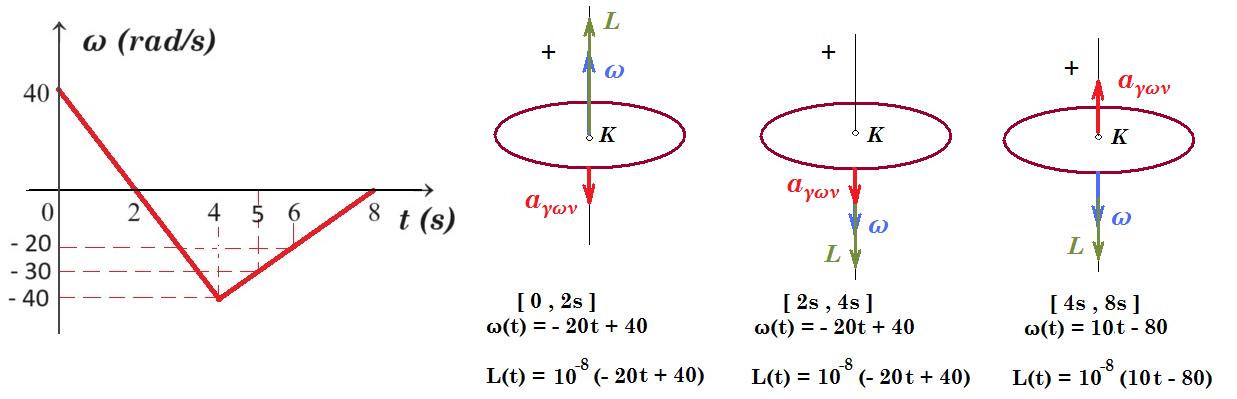
[ 0 , 4s ]   α_γων = Δω / Δt  = ( 0 - 40 rad/s ) / (2s - 0 ) = - 20 rad/s²          ω(t) = - 20.t + 40

       ω(4) = - 20.4 + 40 = - 80 + 40  =>  ω(4) = - 40 rad/s         

[ 4s , 8s ]  α_γων = Δω / Δt  = ( 0 - (- 40 rad/s) ) / (8s - 4s ) = + 10 rad/s²   

  ω = 10.t + β  =>  - 40 = 10.4 + β  =>  β = - 80     ω(t) = 10.t - 80   ή  ω(t) = 10.(t - 4) - 40

   Να βρεθεί η γωνιακή μετατόπιση του δίσκου στο χρονικό διάστημα  3s-5s    

  ω(t) = - 20.t + 40  =>   ω(3) = - 20.3 + 40  =>  ω(3) = - 20 rad/s 

  ω(t) = 10.t - 80  =>   ω(4) = 10.4 - 80  =>  ω(4) = - 40 rad/s         

                                  ω(5) = 10.5 - 80  =>  ω(5) = - 30 rad/s 

από τα εμβαδά του διαγράμματος  ω(t) 

χρονικό διάστημα  [ 3s , 4s ]  μια ακτίνα του δίσκου "διαγράφει γωνία" [- 40 + (- 20)].(4 - 3) / 2 = - 30 rad      

χρονικό διάστημα  [ 4s , 5s ]  μια ακτίνα του δίσκου "διαγράφει γωνία" [- 40 + (- 30)].(5 - 4) / 2 = - 35 rad    

  άρα  στο χρονικό διάστημα    [ 3s , 5s ]  μια ακτίνα του δίσκου "διαγράφει γωνία"  - 65 rad    

ΘΕΜΑ Β2

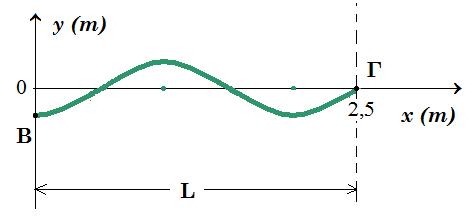
Κατά μήκος ενός γραμμικού ελαστικού μέσου, διαδίδεται ένα αρμονικό κύμα, προς την θετική κατεύθυνση (προς τα δεξιά) με πλάτος Α=0,2m με συχνότητα  f=1Ηz και στο σχήμα δίνεται η μορφή ενός τμήματος  ΒΓ του μέσου, μια στιγμή την οποία θεωρούμε ως αρχή μέτρησης του χρόνου (t₀=0), όπου L=2,5m.  Τη στιγμή αυτή η ταχύτητα ταλάντωσης του σημείου Β είναι μηδενική.

Β2.(α)  Σχεδιάστε την μορφή του τμήματος ΒΓ, την χρονική στιγμή t₁=2,25s.           μονάδες 5

Β2(β)  Το κύμα προσπίπτει κάθετα σε επίπεδη επιφάνεια οπότε ανακλάται χωρίς απώλεια ενέργειας. Το οδεύον και το ανακλώμενο κύμα συμβάλλουν με συνέπεια να δημιουργηθεί στάσιμο κύμα.  Εάν το σημείο Β είναι κοιλία γράψτε την εξίσωση του στασίμου κύματος. Πόσες κοιλίες δημιουργούνται στο τμήμα ΒΓ;  μονάδες 5 + 5  

ΘΕΜΑ Β2          ΛΥΣΗ

L = 5λ/4 = 2,5 m => λ = 2 m        v = λ f = 2 m 1 Hz = 2 m/s       ω = 2πf = 2π rad/s       f = 1 Hz => T = 1s

y(x,t) = A ημ(2πt/T - 2πx/λ + φ) = 0,2 ημ(2πt - 2πx/2 + φ) = 0,2 ημ(2πt - πx + φ)  

y(x,t=0) = - 0,2 συν(πx)  = - 0,2 ημ(π/2 - πx) = 0,2 ημ(π/2 - πx + π) = 0,2 ημ( - πx + 3π/2)  

    άρα   y(x,t) = 0,2 ημ(2πt - πx + 3π/2)         

   υ(x,t)  =  0,4π συν(2πt - πx + 3π/2)         α(x,t)  = - 0,8π² ημ(2πt - πx + 3π/2)    

      2,25 s =  2 s  + 0,25 s  =  T + T/4  

y(x , t=2,25s) = 0,2 ημ(2π 2,25 - πx + 3π/2) = 0,2 ημ(4,5π - πx + 3π/2) = 0,2 ημ(6π - πx) = - 0,2 ημ(πx)   

εξίσωση στασίμου κύματος :   y(x,t) = 0,4 συν(πx) ημ(2πt + θ)    

κοιλίες :   συν(π.x) = ± 1  =>  π.x =  Ν.π  =>  x =  Ν   Ν = 0, 1, 2, 3, ...

0 £ x £ 2,5  => 0 £ Ν £ 2,5 =>  Ν = 0, 1, 2       άρα  x_κ = 0 m   1 m   2 m   η θέση των κοιλιών

ΘΕΜΑ Β3

Δύο σώματα Σ1 και Σ2 με μάζες m₁ και m₂ αντίστοιχα, κινούνται το ένα προς το άλλο πάνω σε λείο οριζόντιο επίπεδο με ταχύτητες μέτρων υ₁ = υ και υ₂ = 2υ αντίστοιχα. Το σώμα Σ1 έχει κινητική ενέργεια ίση με 6 J.
Κάποια στιγμή τα δύο σώματα συγκρούονται κεντρικά και ελαστικά με αποτέλεσμα μετά την κρούση το σώμα Σ1 να ακινητοποιείται. Επαναλαμβάνουμε τη διαδικασία αλλά αυτή τη φορά τα δύο παραπάνω σώματα Σ1 και Σ2 κινούνται στο λείο οριζόντιο επίπεδο με ταχύτητες μέτρων υ₁ και υ₂, σε διευθύνσεις κάθετες μεταξύ τους και κάποια στιγμή συγκρούονται πλαστικά. Βρείτε την απώλεια ενέργειας λόγω της πλαστικής κρούσης.  μονάδες 10

ΘΕΜΑ Β3        ΛΥΣΗ      

 v₁' = 0  =>  (m₁ - m₂) v  +  2 m₂ (- 2v)  =  0   =>  m₁ = 5m₂       

 διατήρηση ορμής πλαστική κρούση  οι ορμές είναι κάθετες πριν την κρούση

  m₁² v²  +  m₂² (2v)² =  (m₁ + m₂)² u²  =>  25 m₂² v²  +  m₂² 4 v² =  36 m₂² u²  =>  29 v² = 36 u²  

  ΔΚ =  ½ (m₁ + m₂) u²  -  ½ m₁ v²  -  ½ m₂ (2v)² =  ½  6 m₂ u²  -  ½  5m₂ v²  -  ½  m₂ 4 v²  = 

   =  ½  6 m₂  29/36 v²  -  ½  9 m₂ v²  =   ½  m₂  29/6 v²  -  ½  9 m₂ v² =  (29 - 54)/6  ½  m₂  v²  =

   =  - 25/6  ½  m₁/5  v²  =  - 5/6  ½  m₁  v² =  - 5/6  6 J = - 5 J

            επαλήθευση :

 v₂'  =  (m₂ - m₁) (- 2v) / (m₁ + m₂)  +  2 m₁ v / (m₁ + m₂)  = (m₂ - 5m₂) (- 2v) / 6.m₂  +  2  5m₂ v / 6.m₂  = 

      =  8 m₂ v / 6.m₂  +  10 m₂ v / 6.m₂  =>   v₂' = 3 v     

 K₁ = ½ m₁ v² = 6 J         K₂ = ½ m₂  ( 2v )² = ½  m₁/5  4 v²  =  4/5  6 J  =  4,8 J 

  K_1,2  =  ½  6m₂  u²  = ½  6m₂  29/36 v²  = ½  6/5 m₁  29/36 v²  =  29/30  6 J  =  29/5 J  =  5,8 J

  ΔΚ =  K_1,2  -  K₁  -  K₂  =  5,8 J  -  6 J  -  4,8 J  =  - 5 J

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘΕΜΑ Γ

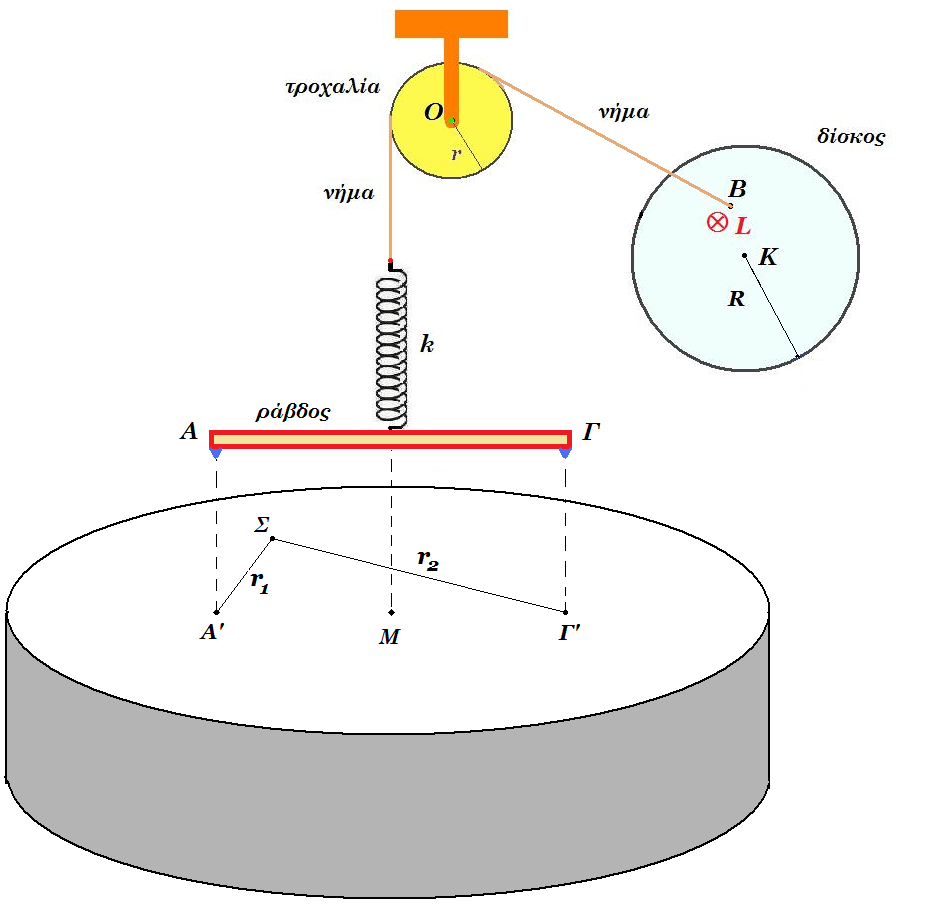
Στην κατακόρυφη διάταξη του σχήματος ο δίσκος ακτίνας R=0,5m περιστρέφεται γύρω από οριζόντιο άξονα χ'χ που διέρχεται από το κέντρο του Κ  και είναι κάθετος στο επίπεδό του. Στοιχειώδης μάζα Δm του δίσκου που βρίσκεται στο σημείο Β έχει κινητική ενέργεια π^.10^-5J , στροφορμή μέτρου 4^.10^-6 kg m²/s. Η ράβδος μάζας m=0,1kg  μήκους d=1m στο κάτω άκρο του ιδανικού ελατηρίου σταθεράς k=100N/m ταλαντώνεται εξ' αιτίας της περιστροφής του δίσκου.  Η επίπεδη τροχαλία έχει μηδαμινή μάζα, ακτίνα r=0,3m.  Το νήμα μπορεί να ολισθαίνει στην περιφέρεια της τροχαλίας χωρίς τριβές. 

Γ1.  Aν διπλασιασθεί η συχνότητα περιστροφής του δίσκου το πλάτος ταλάντωσης της ράβδου 

     (α)  θα αυξηθεί        (β)  θα μειωθεί        (γ)  θα μείνει το ίδιο     μονάδες 2

        Δικαιολογήστε την άποψή σας.     μονάδες 8

Στα άκρα Α, Γ της ράβδου υπάρχουν ακίδες έτσι ώστε καθώς αυτή ταλαντώνεται, ακουμπούν στα σημεία  Α' , Γ'  αντίστοιχα της επιφάνειας υγρού με συνέπεια να δημιουργούνται εγκάρσια κύματα στην επιφάνεια του υγρού με πλάτος Α=2cm.  Η ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού είναι υ=1m/s.  Έστω σημείο Σ της επιφάνειας του υγρού το οποίο απέχει απόσταση  r₁=0,5m   r₂=0,9m  από τα σημεία Α' , Γ'.  

Γ2.  Πόσα σημεία της ευθείας που ορίζεται από τα σημεία Α', Γ' ταλαντώνονται με μέγιστο πλάτος; μονάδες 10

Γ3.  Σχεδιάστε τη γραφική παράσταση της απομάκρυνσης του σημείου Σ συναρτήσει του χρόνου. μονάδες 10

Η ράβδος κατά την ταλάντωσή της παραμένει σε οριζόντια θέση χωρίς να στρέφεται (κινείται στο κατακόρυφο επίπιδο της τροχαλίας και του δίσκου).  

                                      ΛΥΣΗ

Γ1.

 Κ = ½ Δm  υ²         L = Δm  v (KB) 

K / L =  v / 2(KB)  =>  π 10^-5 / 4 10^-6  =  ω_δ / 2  => ω_δ = 5.π rad/s      T = 2π / ω_δ = 2π / 5π = 0,4 s

    ω_δ = v / (KB)   συχνότητα διεγέρτη ( του δίσκου που περιστρέφεται )

αμείωτη απλή αρμονική ταλάντωση  ω₀² = k/m = 100 / 0,1 => ω₀² = 1000 => ω₀ = 10√10 = 10.π rad/s 

για να έχουμε μέγιστο πλάτος ταλάντωσης του Σ  ( συντονισμός )  πρέπει  ω_δ = ω₀   

αν διπασιασθεί η συχνότητα του διεγέρτη  ( δίσκου )   2.ω_δ = 2 . 5.π = 10.π = ω₀   το πλάτος ταλάντωσης της ράβδου θα αυξηθεί  θα γίνει μέγιστο ( συντονισμός ) 

Γ2.

υ = λ / Τ  => λ = υ T =  1 m/s  0,4 s  => λ = 0,4 m 

r₂ - r₁ = Ν λ  = N  0,4m      ταλάντωση με μέγιστο πλάτος

    r₁ + r₂ = Α'Γ' = 1 m =>  2 r₂  =  Ν 0,4  + 1 =>  r₂ =  0,2 Ν + 0,5  

 πρέπει   0 £  r₂ £  1 m  =>   0 £   0,2 Ν + 0,5  £  1 m  => 

  =>  - 0,5 £   0,2 Ν  £  0,5  =>  - 2,5 £  Ν  £  2,5      Ν  =  -2, -1, 0, 1, 2 

Ν = -2   r₂ = - 0,4 + 0,5 = 0,1 m       r₁ = 0,9 m

Ν = -1   r₂ = - 0,2 + 0,5 = 0,3 m       r₁ = 0,7 m

Ν = 0     r₂ =  0,5 m                        r₁ = 0,5 m

Ν = 1    r₂ = + 0,2 + 0,5 = 0,7 m       r₁ = 0,3 m

Ν = 2    r₂ =  0,4 + 0,5 = 0,9 m         r₁ = 0,1 m        

       Α'    0,1    0,2   0,3    0,4    0,5     0,6     0,7    0,8    0,9     Γ'    

r₂ - r₁ = Ν λ + λ/2  = N  0,4m + 0,2m       απόσβεση

    r₁ + r₂ = Α'Γ' = 1 m =>  2 r₂  =  Ν 0,4  + 0,2 + 1 =>  r₂ =  0,2 Ν + 0,6  

 πρέπει   0 £  r₂ £  1 m  =>   0 £   0,2 Ν + 0,6  £  1 m  => 

  =>  - 0,6 £   0,2 Ν  £  0,4  =>  - 3 £  Ν  £  2      Ν  =  -3, -2, -1, 0, 1, 2 

Ν = -3   r₂ = - 0,6 + 0,6 = 0 m         r₁ = 1 m     απορρίπτεται

Ν = -2   r₂ = - 0,4 + 0,6 = 0,2 m       r₁ = 0,8 m

Ν = -1   r₂ = - 0,2 + 0,6 = 0,4 m       r₁ = 0,6 m

Ν = 0     r₂ =  0,6 m                        r₁ = 0,4 m

Ν = 1    r₂ = + 0,2 + 0,6 = 0,8 m       r₁ = 0,2 m

Ν = 2    r₂ =  0,4 + 0,6 = 1 m           r₁ = 0 m     απορρίπτεται

εστω  σημείο Ρ της ευθείας  (Α'Γ')  εκτός του ευθυγράμμου τμήματος Α'Γ' προς το μέρος του Α'  έχουμε :  (ΡΑ') - (ΡΓ') = (Α'Γ') = 1 m =  2 . 0,4 m + 0,2 m = 2.λ + λ/2   άρα το σημείο  Ρ  είναι ακίνητο σημείο απόσβεσης  

Γ3.

πρώτα φθάνει το κύμα από το σημείο Α' σε χρόνο  t₁ = r₁ / v = 0,5 / 1 = 0,5 s     y_Σ(t) = 0      0 £  t £  0,5 s  

y_Σ = A ημ(2π.t/T - 2π.r₁/λ) = 0,02 ημ(5π.t - 2π.0,5/0,4) => y_Σ(t) = 0,02 ημ(5π.t - 5π/2)    0,5 s £  t £  0,9 s     Τ=0,4 s   

μετά φθάνει το κύμα από το σημείο Γ' σε χρόνο  t₂ = r₂ / v = 0,9 / 1 = 0,9 s   οπότε έχουμε συμβολή των δύο κυμάτων :

y_Σ = A ημ(2π.t/T - 2π.r₁/λ)  + A ημ(2πt/T - 2π.r₂/λ) =  0,02 ημ(5π.t - 2π.0,5/0,4)  +  0,02 ημ(5π.t - 2π.0,9/0,4)  =

   =  0,04  συν[π.(0,9 - 0,5) / 0,4]  ημ[5π.t - π.(0,9 + 0,5) / 0,4]  =  0,04  συνπ  ημ[5π.t - π.1,4 / 0,4] = - 0,04 ημ(5π.t - 7π/2) 

=>  y_Σ(t) = - 0,04 ημ(5π.t - 7π/2)  = - 0,04 συν(5π.t)      t ³  0,9 s         Τ = 0,4 s 

ημ(5π.t - 7π/2) = - συν(5π.t) ημ(7π/2)  =  συν(5π.t)

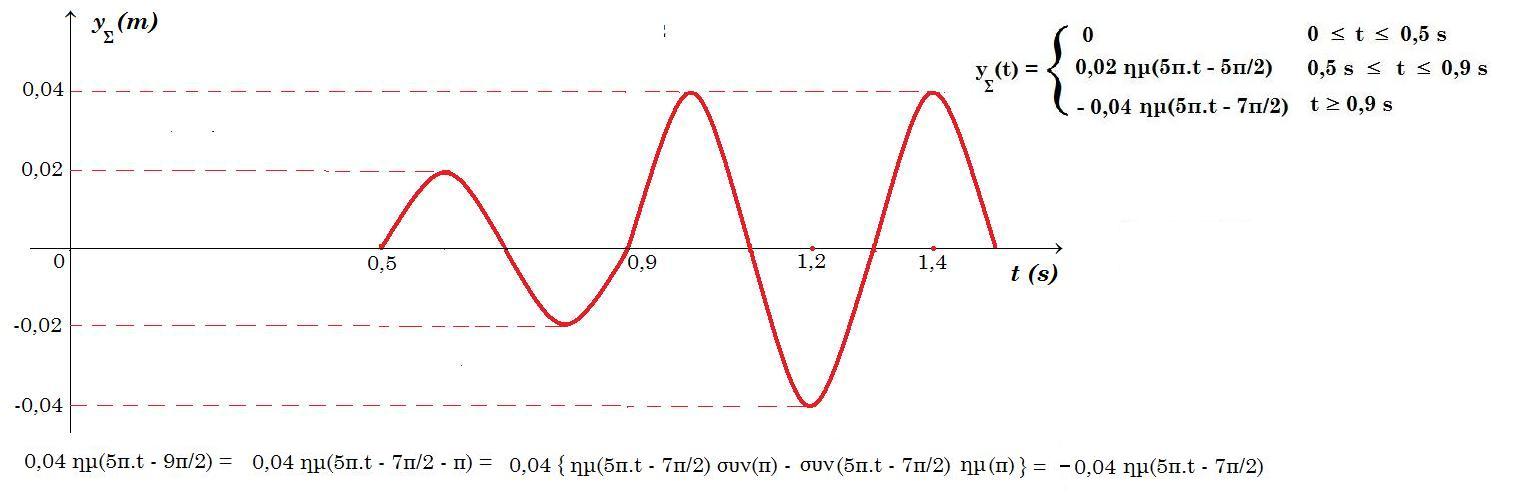
  y_Σ(t)  =  0,02 ημ(5π.t - 2π.0,5/0,4)  +  0,02 ημ(5π.t - 2π.0,9/0,4)  =  0,02 ημ(5π.t - 2,5.π)  +  0,02 ημ(5π.t - 4,5.π)  

t = 0,9 s   0,02 ημ(5π.t - 2,5.π)  +  0,02 ημ(5π.t - 4,5.π) = 0,02 ημ(5π.0,9 - 2,5.π) + 0,02 ημ(5π.0,9 - 4,5.π)  =

               =  0,02 ημ(4,5.π - 2,5.π)  =  0

t = 1 s      0,02 ημ(5π.t - 2,5.π)  +  0,02 ημ(5π.t - 4,5.π)  =  0,02 ημ(5π - 2,5.π)  +  0,02 ημ(5π - 4,5.π)  =

               =  0,02 ημ(2,5.π) +  0,02 ημ(π/2)  =  0,02 + 0,02 = 0,04 m

t = 1,2 s   0,02 ημ(5π.t - 2,5.π)  +  0,02 ημ(5π.t - 4,5.π)  =  0,02 ημ(5π.1,2 - 2,5.π) + 0,02 ημ(5π.1,2 - 4,5.π) =

    =  0,02 ημ(6π - 2,5.π) +  0,02 ημ(6π - 4,5.π)  =  0,02 ημ(3,5.π) +  0,02 ημ(1,5.π)  =  - 0,02  - 0,02 = - 0,04 m

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘEΜΑ Δ 

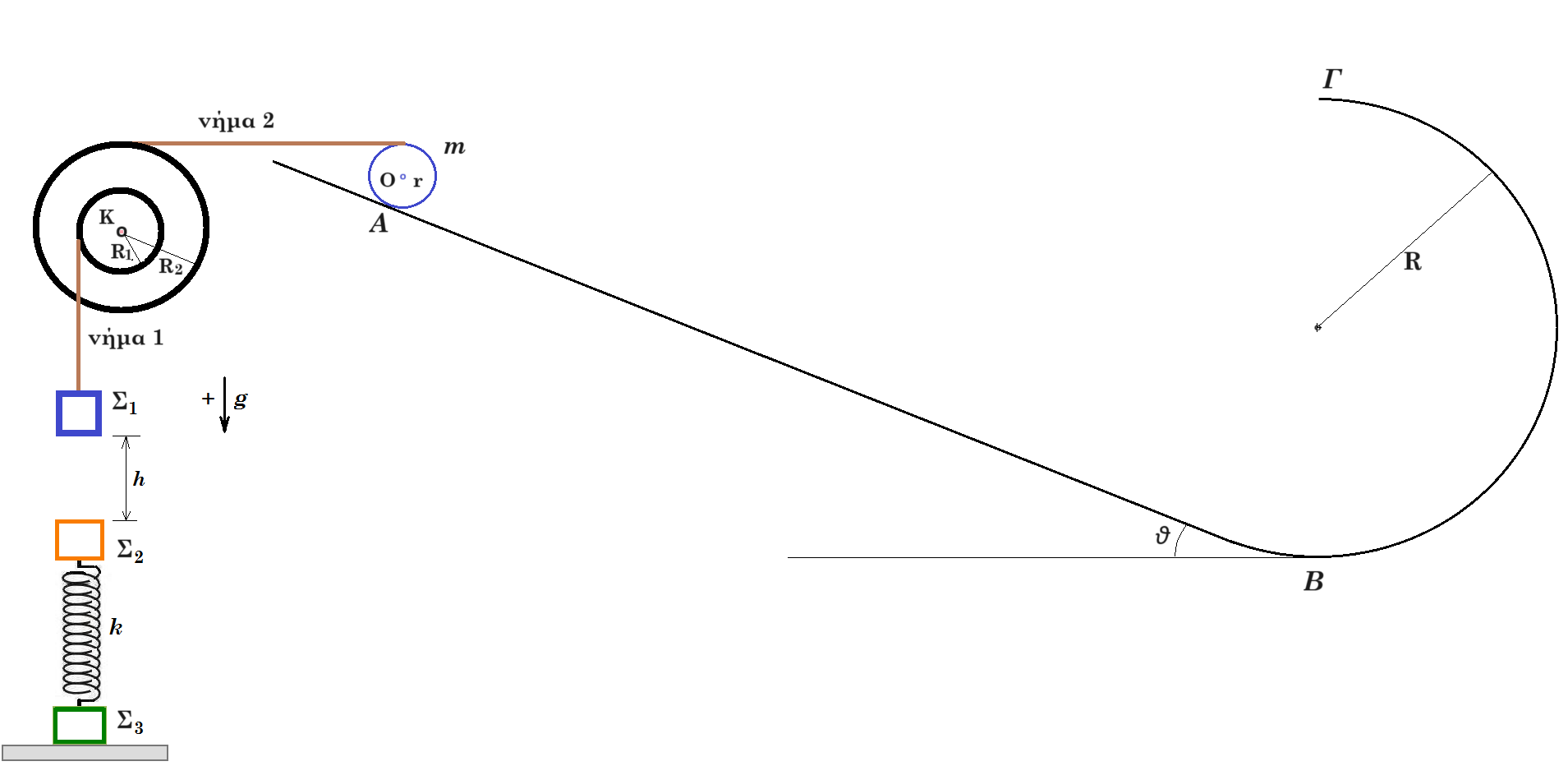
Θεωρούμε την διάταξη του σχήματος, σε κατάσταση ισορροπίας, σε κατακόρυφο επίπεδο.   Στη θέση Α  του κεκλιμένου επιπέδου ισορροπεί κυκλική στεφάνη μάζας m=3kg ακτίνας r=0,1m.  Το κεκλιμένο επίπεδο γωνίας κλίσεως θ, ( ημθ = 0,6  συνθ = 0,8 ) στην βάση του συνδέεται με κατακόρυφο ημικύκλιο ακτίνας R=1m.  Η στεφάνη στο άνω της άκρο συνδέεται με οριζόντιο αβαρές μη εκτατό νήμα 2 (σταθερού μήκους) με τροχαλία μάζας Μ  εσωτερικής ακτίνας R₁=0,3m  εξωτερικής ακτίνας R₂=0,5m.  Η τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από άξονα που διέρχεται από το κέντρο της Κ ( σταθερό ακίνητο σημείο )  και είναι κάθετος στο επίπεδο της. Γύρω από την τροχαλία έχουμε τυλίξει αρκετές φορές αβαρές μη εκτατό νήμα 1  το οποίο συνδέεται με σώμα Σ₁.  Κάτω από το σώμα Σ₁ σε κατακόρυφη απόσταση h ισορροπεί σώμα Σ₂ "δεμένο" στο άνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k.  Στο κάτω άκρο του ελατηρίου είναι "δεμένο" σώμα Σ₃ το οποίο ακουμπά σε οριζόντιο δάπεδο.  k = 200 N/m   m₁ = 1 kg   m₂ = 1 kg   m₃ = 3 kg           

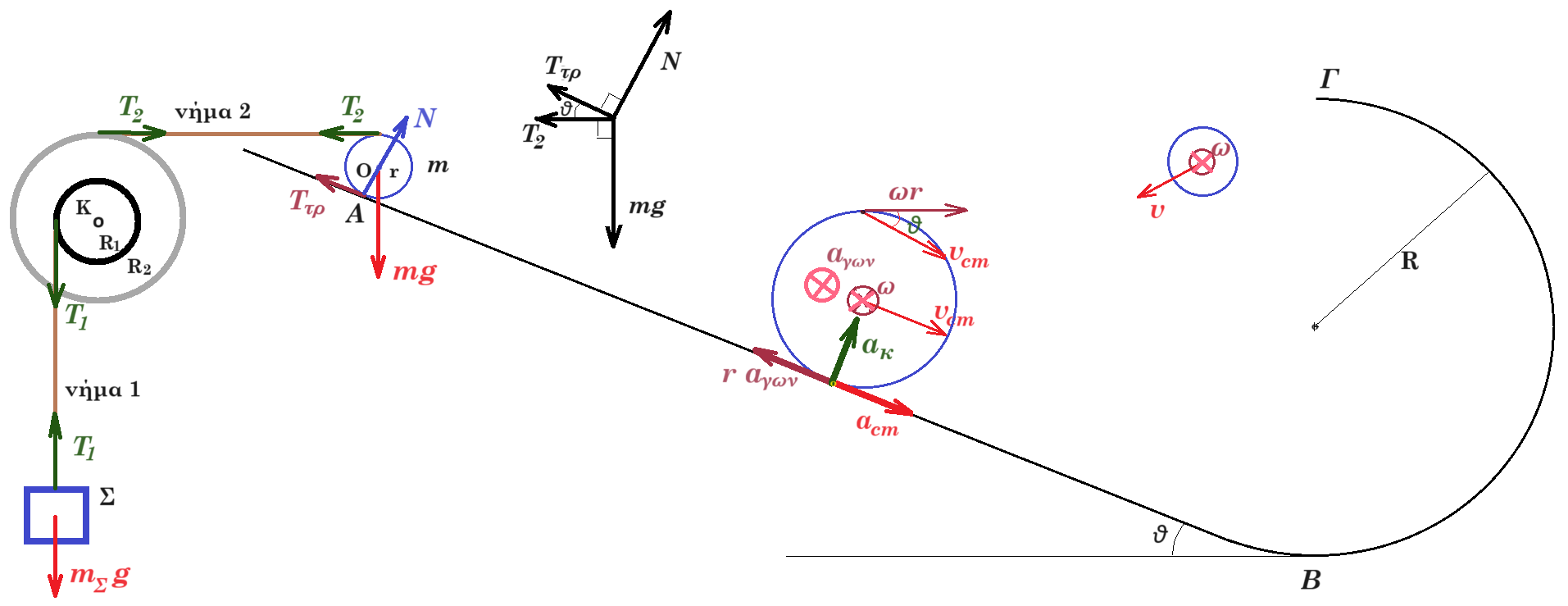
Κάποια στιγμή ( t₀ = 0 ) αφαιρούμε το νήμα 2,  οπότε το σώμα Σ₁ κινείται κατακόρυφα προς τα κάτω ενώ  η τροχαλία περιστρέφεται γύρω από τον άξονά της χωρίς τριβές με σταθερή γωνιακή επιτάχυνση α_γων = 10/3 rad/s² και  η στεφάνη κατέρχεται επί του κεκλιμένου επιπέδου κυλιόμενη (δεν ολισθαίνει). ενώ το κέντρο της έχει επιτάχυνση  α_cm = 3 m/s².   

Δ1.  Τη χρονική στιγμή t₁=1s  βρείτε την ταχύτητα του ανώτερου σημείου της στεφάνης  καθώς και την επιτάχυνση του σημείου επαφής της στεφάνης με το κεκλιμένο επίπεδο.  μονάδες 5+5

Δ2.  Η στεφάνη κυλίεται (δεν ολισθαίνει) κινούμενη στο κεκλιμένο επίπεδο,  ανέρχεται κυλιόμενη στο ημικύκλιο  και διέρχεται από την ανώτατη θέση Γ του ημικυκλίου έχοντας ταχύτητα μέτρου 3m/s.  Βρείτε την δύναμη που δέχεται από το ημικύκλιο στο σημείο Γ και  την γωνιακή ταχύτητάς της ( διεύθυνση, φορά, μέτρο )  μετά από 0,2sec  αφού περάσει το σημείο Γ. μονάδες 5+5      

Δ3.  Το σώμα Σ₁ συγκρούεται κεντρικά πλαστικά με το σώμα Σ₂  οπότε το συσσωμάτωμα αρχίζει να εκτελεί Α.Α.Τ. Βρείτε το ύψος h έτσι ώστε το σώμα Σ₃  οριακά δεν εγκαταλείπει το οριζόντιο δάπεδο. ( θετική κατεύθυνση κατακόρυφη προς τα κάτω )  μονάδες 10

Δ4.  Έστω ότι ο χώρος όπου ταλαντώνεται το συσσωμάτωμα εμποδίζει αυτό να κινηθεί ασκώντας του δύναμη F=-0,2.v.  Γράψτε την εξίσωση της απομάκρυνσης του συσσωματώματος συναρτήσει του χρόνου  και σχεδιάστε αυτήν.  Θεωρούμε τη στιγμή t=0 αρχικό πλάτος ταλάντωσης Α=0,2m. μονάδες 5   g = 10 m/s²   

                                  ΛΥΣΗ

Δ1.   a_cm = α_γων r  =>  3 m/s²  = α_γων  0,1 m  =>  a_γων = 30 rad/s²       ω = α_γων t = 30 rad/s² 1 s = 30 rad/s    

           υ_cm = = ω r = 30 rad/s  0,1 m = 3 m/s  

  υ²  =  υ_cm²  +  (ω r)²  +  2 υ_cm  ω r  συνθ  =  2 υ_cm² ( 1 + συνθ ) = 2 3²  (1 + 0,8 ) =  18  1,8 = 18²/10  =>

     =>   υ  = 18/√10 m/s = 18/π m/s    

στο σημείο Ε  η στεφάνη  έχει  τρεις επιταχύνσεις  την επιτάχυνση του κέντρου μάζας ,  την γωνιακή  και  την  κεντρομόλο    αλλά  η επιτάχυνση του κέντρου μάζας  και η γωνιακή είναι αντίθετες και έχουν συνισταμένη μηδέν  ενώ   η κεντρομόλος ισούται με  α_κ  =  υ² / r  =  ω² r  =  30²  0,1  =  90 m/s²    

Δ2.  όταν η στεφάνη διέρχεται από την ανώτερη θέση Γ  υ_Γ = 3 m/s :  ΣF_y = F_κ  =>  mg  + Ν = m v_Δ²/(R - r)  => 

=> 30  + Ν =  3  3² / (1 - 0,1)  =>  Ν  =  27/0,9 - 30 = 0   άρα μόλις διέρχεται από την ανώτερη θέση Γ του ημικυκλίου  διότι ισχύει Ν=0  

η στεφάνη στον αέρα δεν δέχεται δύναμη που να δημιουργεί ροπή  συνεπώς  η γωνιακή ταχύτητά της είναι σταθερή

      ω = υ_Γ / r = 3 m/s  /  0,1 m  = 30 rad/s

Δ3.   επιτάχυνση σώματος Σ₁ :  a₁ = α_γων R₁ =  10/3 rad/s²  0,3 m  = 1 m/s²   

ταχύτητα σώματος Σ₁ :  v₁ = a₁ t = 1 t       h = ½  a₁  t² =>  h =  v₁² / 2.a₁  =  v₁² / 2  =>  v₁² = 2h   (1)  

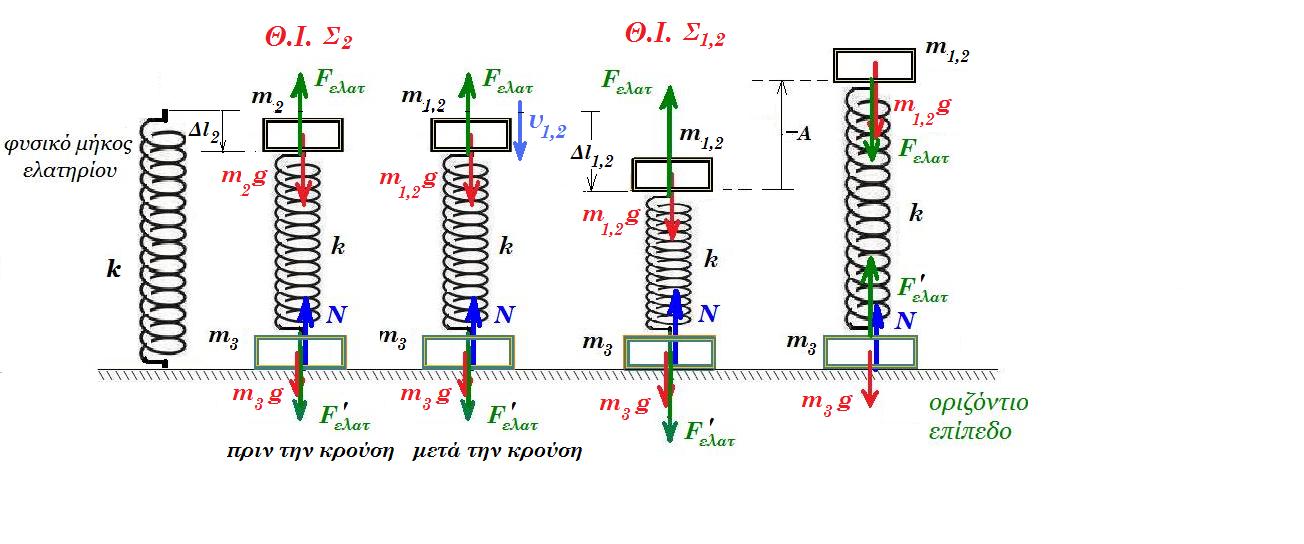
ισορροπία Σ₂ :  m₂ g  =  k Δl₂  =>  Δl₂  = m₂ g / k =  1 10 / 200 = 0,05 m    αρχική συσπείρωση ελατηρίου

πλαστική κρούση  διατήρηση ορμής :  m₁ v₁ = (m₁ + m₂) v_1,2  =>  v₁ = 2.v_1,2  =>  v_1,2 = v₁/2 =>  v_1,2² = v₁² / 4 = h/2  (2)

ισορροπία συσσωματώματος : (m₁ + m₂) g  =  k Δl_1,2  =>  Δl_1,2  = (m₁ + m₂) g / k =  2 10 / 200 = 0,1 m    συσπείρωση ελατηρίου

 ω² =  k / m_1,2 =  200 / 2  => ω = 10 rad/s  

½ k ( Δl_1,2 - Δl₂ )² + ½ (m₁ + m₂) v_1,2² = ½ k A²  => 200  0,0025  +  2  h/2 = 200 A²  =>  0,5 + h = 200 A²    (3)

 x  =  A ημ(10t + φ)        υ  =  10.A συν(10t + φ)         α  =  - 100.A ημ(10t + φ)

   x(0) = - 0,05 m = Α ημ(φ)  =>  ημ(φ) = - 0,05 / Α  

ΣF = m a  => (m₁ + m₂) g  + F_ελατ = (m₁ + m₂) a  =>  20 + F_ελατ = - 2  100.A ημ(10t + φ) => F_ελατ = - 20 - 200.x

στο σώμα Σ₃  ασκείται αντίθετη δύναμη ελατηρίου :  F_ελατ' = + 20 + 200.x 

ισορροπία Σ₃ :  m₃ g  +  Ν  + F_ελατ' = 0  =>  30 + Ν + 20 + 200.x = 0  =>^Ν=0  30 + 20 + 200.(- Α) = 0  =>

                     =>  30  + 20  -  200.Α  = 0  =>  Α=0,25m   (4)  

  (3) , (4)  =>  0,5  +  h  =  200  0,0625 = 12,5  =>  h = 12 m     

άλλος τρόπος : 

για να ανασηκωθεί το σώμα Σ₃  πρέπει η δύναμη του ελατηρίου να έχει κατεύθυνση προς τα πάνω  και  μέτρο τουλάχιστον ίσο με το βάρος του    αλλά τότε το ελατήριο θα είναι επιμηκυμένο   έστω  x  η επιμήκυνση του ελατηρίου  τότε :   k x ³ m₃ g  =>  200  x ³  3  10  =>   x ³  30/200  =>   x ³  0,15 m         αλλά η  Θ.Ι.  του συσσωματώματος είναι όταν το ελατήριο είναι συσπειρωμένο κατά  Δl_1,2 = 0,1 m     

συνεπώς το πλάτος της ταλάντωσης του συσσωματώματος ικανοποιεί την σχέση :  Α  ³   0,1 m  +  0,15 m  =>  Α ³  0,25 m      

                       επαλήθευση

h = ½ a₁ t² =>  12 = ½ 1 t² => t² = 24     v₁² = a₁² t² = 1 24 = 24     v_1,2 = v₁/2 => v_1,2² = v₁² / 4 = 24/4 = 6  =>  v_1,2 = √6 m/s

διατήρηση ενέργειας για την ταλάντωση του συσσωματώματος :

½ k ( Δl_1,2 - Δl₂ )² + ½ (m₁ + m₂) v_1,2² = ½ k A²  => 200 ( 0,05 )² + 2  6 = 200 A²  => 0,5 + 12 = 200 A² => A=0,25m 

 x = 0,25 ημ(10t + φ)         υ = 2,5 συν(10t + φ)         α = - 25 ημ(10t + φ) = - 100.x = - ω² x

 x(0) = - 0,05 m = 0,25 ημ(φ)  =>  ημφ = - 0,05 / 0,25 = - 1/5       συνφ =  ± √( 1 - ημ²φ )  =  ± √( 1 - 1/25 ) = ± √24/5  =  ± 2√6/5 =  ± 0,4√6

  τη στιγμή  t=0 το συσσωμάτωμα είναι 0,05 m πάνω από τη Θ.Ι. του  για αυτό η απομάκρυνση x είναι αρνητική  και  η επιτάχυνση θετική   α = - ω² x    x < 0  άρα  α > 0   οπότε ΣF > 0  κατακόρυφη προς τα κάτω    η ταχύτητα του συσσωματώματος είναι  υ_1,2 (0) = 2,5 συν(φ) = 2,5  0,4√6 = + √6 m/s

ΣF = m a  => (m₁ + m₂) g  + F_ελατ = (m₁ + m₂) a  =>  20 + F_ελατ = - 2  25 ημ(10t + φ) => F_ελατ = - 20 - 200.x

F_ελατ(t) = - 20 - 50 ημ(10t + φ)         F_ελατ(0) = - 20 - 50 ημ(φ) = - 20 - 50 (- 1/5) = - 10 N

Δ4.     Λ = b / 2.m_1,2 = 0,2 / 2.2 = 0,05 s^-1        A(t) = A₀ e^-Λ.t  =  0,2 e^-0,05.t    

         x(t) =  0,2 e^-0,05.t  συν(10.t)       x(0) = 0,2 m   T = π/5 s