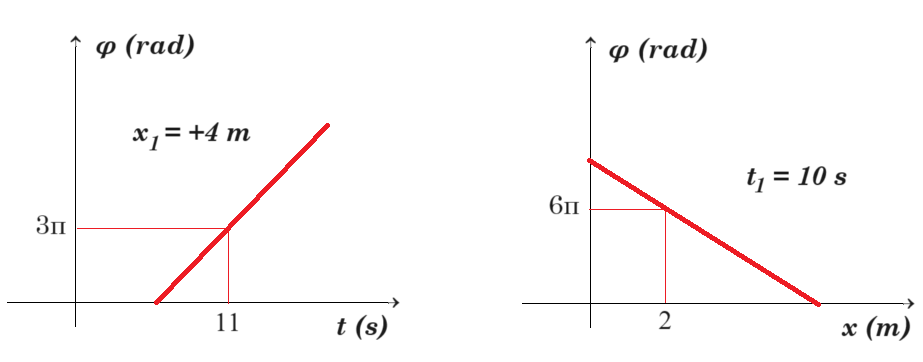
Δύο σώματα Σ1 και Σ2 με μάζες m1 και m2 αντίστοιχα, κινούνται το ένα προς το άλλο πάνω σε λείο οριζόντιο επίπεδο με ταχύτητες μέτρων υ₁ = υ και υ₂ = 2υ αντίστοιχα. Το σώμα Σ1 έχει κινητική ενέργεια 6 J.  Κάποια στιγμή τα δύο σώματα συγκρούονται κεντρικά και ελαστικά με αποτέλεσμα μετά την κρούση το σώμα Σ1 να ακινητοποιείται.  Επαναλαμβάνουμε τη διαδικασία αλλά αυτή τη φορά τα δύο παραπάνω σώματα Σ1 και Σ2 κινούνται στο λείο οριζόντιο επίπεδο με ταχύτητες μέτρων υ₁ και υ₂, σε διευθύνσεις κάθετες μεταξύ τους και κάποια στιγμή συγκρούονται πλαστικά. Βρείτε την απώλεια ενέργειας λόγω της πλαστικής κρούσης.   

  v₁' = 0  =>  (m₁ - m₂) v  =  2 m₂ 2v  =>  m₁ = 5m₂       

 διατήρηση ορμής πλαστική κρούση  οι ορμές είναι κάθετες πριν την κρούση

  25 m₂² v²  +   m₂² 4 v²  =  36 m₂² u²  =>  29 v² = 36 u²  

   ½  6 m₂ u²  -  ½  5m₂ v²  -  ½  m₂ 4 v²  =  ½ 6 m₂  29/36 v²  -  ½  9 m₂ v²  =  

=  ½  m₂  29/6 v²  -  ½  9 m₂ v² =  - 25/6  ½  m₂  v²  =  - 25/6  ½  m₁/5  v²  =  - 5/6  ½  m₁  v² =- 5/6  6 J = - 5 J

Β2.  Δύο σώματα Σ1 και Σ2 με μάζες m₁ και m₂ αντίστοιχα, κινούνται το ένα προς το άλλο πάνω σε λείο οριζόντιο επίπεδο με ταχύτητες μέτρων υ₁ = υ και υ₂ = 2υ αντίστοιχα. Το σώμα Σ1 έχει κινητική ενέργεια ίση με Κ.  Κάποια στιγμή τα δύο σώματα συγκρούονται κεντρικά και ελαστικά με αποτέλεσμα μετά την κρούση το σώμα Σ2 να ακινητοποιείται.  Επαναλαμβάνουμε τη διαδικασία αλλά αυτή τη φορά τα δύο παραπάνω σώματα Σ1 και Σ2 κινούνται στο λείο οριζόντιο επίπεδο με ταχύτητες μέτρων υ₁ και υ₂, σε διευθύνσεις κάθετες μεταξύ τους και κάποια στιγμή συγκρούονται πλαστικά. Η απώλεια ενέργειας λόγω της πλαστικής κρούσης είναι ίση με:   9 K      10/3 K     17/3 K      17/9 K

  v₂' = 0  =>  (m₂ - m₁) 2v  =  2 m₁ v  =>  m₂ = 2 m₁            m₁² v²  +  4 m₁² 4 v²  =  9 m₁² u²  =>  17 v² = 9 u²  

    0,5 3 m₁ u²  -  0,5 m₁ v²  -  0,5 2 m₁ 4 v²  =  0,5 3 m₁ 17/9 v²  -  0,5 m₁ v²  -  0,5 2 m₁ 4 v²  =  

=  0,5  m₁ 17/3 v²  -  9 0,5 m₁ v²  =  17/3  K  -  9  K  =  - 10/3 K

B2. Εγκάρσιο αρμονικό κύμα διαδίδεται κατά μήκος γραμμικού ελαστικού μέσου προς την κατεύθυνση του θετικού ημιάξονα Οx. Η ταλάντωση του σημείου Ο είναι y = Aημωt. Στα σχήματα φαίνονται η γραφική παράσταση της φάσης σε συνάρτηση με το χρόνο ενός υλικού σημείου Κ του μέσου που βρίσκεται στη θέση x_K = x₁ = +4 m και η γραφική παράσταση της φάσης σε συνάρτηση με τη θέση των σημείων για τη χρονική στιγμή t₁ = 10 s.  Η ταχύτητα διάδοσης του κύματος είναι:   α. 0,5 m/s.     β. 1 m/s.    γ. 2 m/s.         

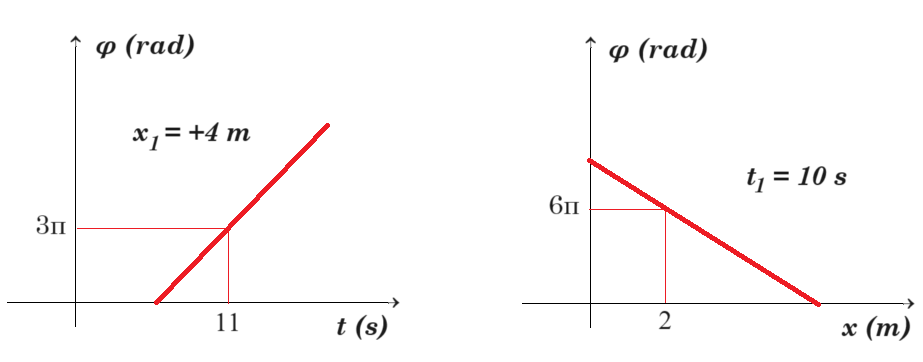
  φ  =  2π/Τ . t  - 2π/λ . x  

  3π  =  2π/Τ . 11  - 2π/λ . 4  =>  3  =  22/Τ  -  8/λ    (1)

  6π  =  2π/Τ . 10  - 2π/λ . 2  =>  6  =  20/Τ  -  4/λ  =>  - 12  =  - 40/Τ  +  8/λ    (2)

  (1) + (2) =>  - 9 = - 18/T  =>  T = 2 s     f = 0,5 Hz     

  (1)  =>  3  =  22/2  -  8/λ  =>  3  -  11  =  - 8/λ  =>  λ = 1 m        v = λ / T = 1 / 2 = 0,5 m/s     

Β3.  Η διπλή ομογενής τροχαλία του σχήματος (καρούλι) έχει μεγάλη ακτίνα R και μικρή r.  Γύρω από τον κύλινδρο της μικρής ακτίνας είναι τυλιγμένο λεπτό αβαρές μη εκτατό νήμα. Ασκούμε στο ελεύθερο άκρο Σ του νήματος οριζόντια δύναμη σταθερού μέτρου F με αποτέλεσμα η αρχικά ακίνητη τροχαλία να αρχίσει την χρονική στιγμή t = 0 να κυλίεται χωρίς να ολισθαίνει προς τα δεξιά εκτελώντας ομαλά μεταβαλλόμενη περιστροφική και μεταφορική κίνηση. Στο χρονικό διάστημα από 0 ως t₁ το σημείο Σ έχει μετατοπιστεί κατά 20 cm και το κέντρο μάζας του δίσκου κατά 30 cm. Αν την χρονική στιγμή t₁ η ταχύτητα του κέντρου μάζας του δίσκου είναι υ_cm, το σημείο Α του μικρού κυλίνδρου, που είναι το αντιδιαμετρικό σημείο του σημείου στο οποίο είναι δεμένο το νήμα στον μικρό κύλινδρο, έχει την ίδια χρονική στιγμή ταχύτητα υ_Α μέτρου:   υ_Α = 5/4 υ_cm      υ_Α = 4/3 υ_cm      υ_Α = 3/2 υ_cm      υ_Α = 3/4 υ_cm       

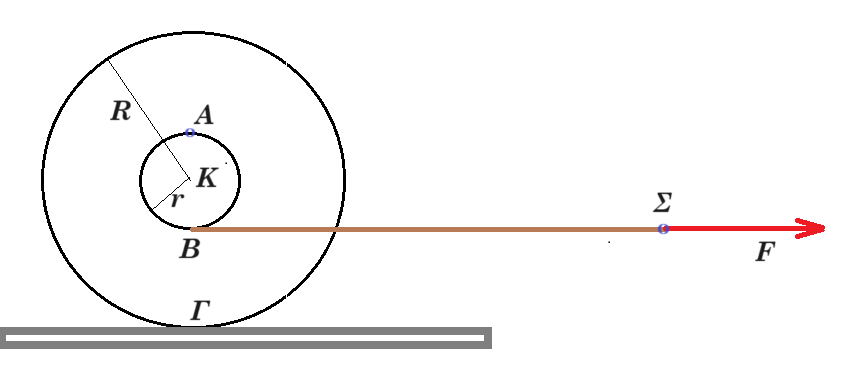
  x_cm / x_Σ  =  R / (R - r)  =  30 / 20  =>  2R = 3R - 3r  =>  R = 3r          ω = v_cm / R  

  v_A  =   v_cm  +  ω r  =  v_cm  +  v_cm r / R  =  ( 1 + 1/3 ) v_cm  =  4/3 v_cm           

ΘΕΜΑ Γ
Εγκάρσιο αρμονικό κύμα διαδίδεται σε γραμμικό ελαστικό μέσο προς το θετικό ημιάξονα Οx. Το υλικό σημείο που βρίσκεται στην αρχή Ο του άξονα ξεκινάει την ταλάντωσή του τη χρονική στιγμή t = 0 από τη θέση ισορροπίας κινούμενο προς τη θέση της μέγιστης θετικής απομάκρυνσης.  Η ταχύτητα ταλάντωσης του σημείου Ο μηδενίζεται για 2η φορά τη χρονική στιγμή t₁ = 0,3 s ενώ το συνολικό μήκος της διαδρομής που έχει διανύσει το σημείο Ο στο χρονικό διάστημα από 0 ως t₁ είναι ίσο με 0,6m. Τη χρονική στιγμή t₂ = 2t₁ ξεκινάει την ταλάντωσή του το σημείο Κ που βρίσκεται στη θέση x_Κ = +0,6 m.
Γ1. Ποια είναι η ταχύτητα διάδοσης του κύματος;   (Μονάδες 3)
Γ2. Να γράψετε την εξίσωση του κύματος.  (Μονάδες 7)
Γ3. Πόσα σημεία του ελαστικού μέσου που έχουν ξεκινήσει να ταλαντώνονται βρίσκονται τη χρονική στιγμή t₃ = 3t₁ σε ακραία θέση ταλάντωσης;   (Μονάδες 5)
Γ4. Αν η διαφορά φάσης μεταξύ των σημείων Λ και Κ είναι ίση με π/2 rad και το σημείο Λ ξεκίνησε την ταλάντωσή του πριν από το σημείο Κ, να υπολογίσετε την απόσταση των σημείων Κ και Λ τη χρονική στιγμή t₄ = 0,8 s.  (Μονάδες 5)
Γ5. Μεταβάλλουμε τη συχνότητα της πηγής με αποτέλεσμα το σημείο Λ να γίνει το 3ο σημείο μετά το σημείο Ο που βρίσκεται σε αντίθεση φάσης με αυτό. Ποιο είναι το ποσοστό μεταβολής της συχνότητας της πηγής.   (Μονάδες 5) 

t₁ = 3T/4 = 0,3 s => T = 0,4 s            0,6 m = 3 A => A = 0,2 m     v = x_K / t₂ = 1 m/s     λ = υ Τ = 0,4 m

  y (x,t) =  0,2  ημ 2π(t/0,4 - x/0,4)  =  0,2  ημ 5π(t - x)  

  x = v t₃ = 1 m/s 0,9 s = 0,9 m      

ημ 5π(0,9 - x) = ± 1  =>  5π(0,9 - x) = Ν.π + π/2 =>  5(0,9 - x)  =  Ν + 1/2  =>

                                  =>  0,9 - x =  Ν/5 +  0,1 => x = - Ν/5 + 0,8

0 £ x £ 0,9  =>  0 £ - Ν/5 + 0,8  £ 0,9  => - 0,8 £ - Ν/5 £  0,1  =>

                   =>   - 4 £ - Ν £  0,5   Ν = 0, 1, 2, 3, 4        0,8m   0,6m  0,4m  0,2m  0

  φ_Λ - φ_Κ = 5π(t - x_Λ ) - 5π(t - x_Κ ) = π/2  => x_Κ - x_Λ = 0,1  => x_Λ = 0,6 - 0,1 = 0,5 m

y (x_Λ ,t) =  0,2  ημ 5π(t - x_Λ ) =  0,2  ημ 5π(0,8 - 0,5)  =  0,2  ημ (1,5 π) = - 0,2 m 

y (x_Κ ,t) =  0,2  ημ 5π(t - x_Κ ) =  0,2  ημ 5π(0,8 - 0,6)  =  0,2  ημ (π) = 0         

  Δx_Κ,Λ² =  y_Λ²  +  (ΚΛ)²  =  0,2²  +  0,1²  =  0,05  =>   Δx_Κ,Λ  =  0,1√5 m

ΘΕΜΑ Δ
Λεπτή, άκαμπτη ομογενής ράβδος ΑΓ μήκους L  μάζας Μ = 5 kg ισορροπεί με τη βοήθεια οριζόντιου μη εκτατού νήματος ΔK, που συνδέεται στο μέσο της Κ, όπως φαίνεται στο σχήμα.  Το άκρο Α της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο.  Η ράβδος σχηματίζει γωνία θ ( ημθ = 0,6   συνθ = 0,8 ) με τον κατακόρυφο τοίχο.   Στο άκρο Γ έχει στερεωθεί ιδανικό κατακόρυφο ελατήριο σταθεράς k = 100 Ν/m, στο κάτω άκρο του οποίου ισορροπεί δεμένο ένα σώμα μάζας m₁ = 1 kg, όπως φαίνεται στο σχήμα.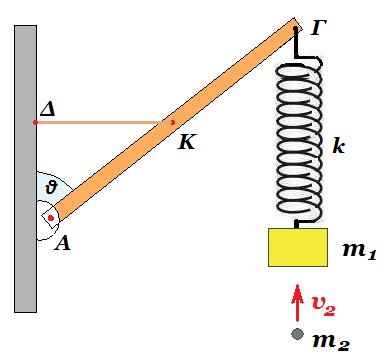
Δ1. Να βρείτε το μέτρο της τάσης του νήματος.   (Μονάδες 6)
Βλήμα μάζας m₂ = 1 kg που κινείται κατακόρυφα με φορά προς τα πάνω συγκρούεται κεντρικά και πλαστικά με το σώμα μάζας m₁ έχοντας ελάχιστα πριν την κρούση ταχύτητα υ₂ = 4 m/s. Το συσσωμάτωμα που δημιουργείται εκτελεί απλή αρμονική ταλάντωση για την οποία θεωρούμε ως χρονική στιγμή t = 0 αμέσως μετά τη στιγμή της κρούσης και θετική φορά προς τα πάνω.
Δ2. Να βρείτε το ποσοστό μεταβολής της κινητικής ενέργειας του βλήματος λόγω της πλαστικής κρούσης.    (Μονάδες 4) 

Δ3. Να βρείτε το μέτρο του ρυθμού μεταβολής της ορμής του συσσωματώματος την χρονική στιγμή που ο ρυθμός μεταβολής της κινητικής ενέργειας της ταλάντωσης του μηδενίζεται για τρίτη φορά μετά την χρονική στιγμή t = 0.    (Μονάδες 6)
Δ4. Να βρείτε τη μέγιστη δυναμική ενέργεια του ελατηρίου κατά τη διάρκεια της ταλάντωσης του συσσωματώματος.    (Μονάδες 4)
Δ5. Να βρείτε το μέγιστο πλάτος ταλάντωσης που θα μπορούσε να έχει το συσσωμάτωμα έτσι ώστε το οριζόντιο νήμα να μη χαλαρώνει οριακά.    (Μονάδες 5)
Να θεωρήσετε ότι:  
• Το μέτρο της επιτάχυνσης της βαρύτητας είναι g = 10 m/s².
• Η αντίσταση του αέρα θεωρείται αμελητέα για όλα τα σώματα.
• Η κρούση γίνεται ακαριαία.
• Κατά την κρούση, δεν έχουμε απώλεια μάζας.