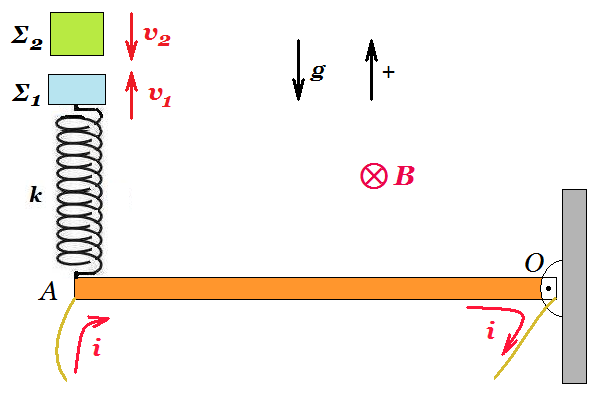
Οριζόντια ομογενής μεταλλική ράβδος μάζας Μ = 0,4 kg  μήκους  L = 1 m , ωμικής αντίστασης 2 Ω oριζόντιο ομογενές μαγνητικό πεδίο εντάσεως Β = 1 Τ ,   τα καλώδια είναι λεπτά και αμελητέας μάζας , το ιδανικό ελατήριο έχει σταθερά  k = 10 N/m , το σώμα Σ1 μάζας m1=0,1kg  εκτελεί Α.Α.Τ.  με πλάτος Α=0,2m

Στη διάρκεια της ταλάντωσης η ράβδος είναι ακίνητη.  Κάποια στιγμή που το σώμα Σ₁ διέρχεται από τη θέση όπου U_ταλ = Ε_ταλ/4  με θετική ταχύτητα και αρνητική επιτάχυνση συγκρούεται κεντρικά - πλαστικά με σώμα Σ₂ μάζας m₂ = 0,3 kg το οποίο κινείται κατακόρυφα προς τα κάτω με ταχύτητα μέτρου υ₂ = Φ3/3 m/s ελάχιστα πριν την κρούση. Θεωρούμε την στιγμή  t = 0 αμέσως μετά την κρούση ενώ παρατηρούμε ότι η ράβδος ισορροπεί σε οριζόντια θέση. 

α)  Βρείτε την εξίσωση της απομάκρυνσης του συσσωματώματος συναρτήσει του χρόνου.

β)  Βρείτε την δύναμη που ασκείται στη ράβδο στο άκρο της Α συναρτήσει του χρόνου.

γ)  Βρείτε την ένταση του ρεύματος που διαρρέει την ράβδο συναρτήσει του χρόνου.

ισορροπία Σ₁ :  m₁ g  =  k Δl_0,1  => Δl_0,1 = 0,1 m   συσπείρωση ελατηρίου  

k = m₁ ω₁² => 10 = 0,1 ω₁²  =>  ω₁ = 10 rad/s       x₁ = 0,2 ημ(10.t + φ)   v₁ = 2 συν(10.t + φ)   a₁ = - 20 ημ(10.t + φ)

U = E/4  =>  x = ± 1/2 0,2 = ± 0,1 m    υ > 0   α < 0   άρα x > 0   x = + 0,1 m  => ημ(10.t + φ) = +1/2

συν(10.t + φ) = +Φ3/2  άρα  υ₁ = +Φ3 m/s  

η κρούση γίνεται σε θέση 0,1 m πάνω από την Θ.Ι. του Σ₁  εκεί όπου το ελατήριο έχει το φυσικό του μήκος 

διατήρηση ορμής κατά την κρούση :  m₁ v₁ - m₂v₂ = (m₁ + m₂) u  =>  0,1 Φ3  -  0,3 Φ3/3  =  0,4  u  =>  u = 0   ακινητοποιείται το συσσωμάτωμα αμέσως μετά την κρούση   όπου το ελατήριο έχει το φυσικό του μήκος 

ισορροπία συσσωματώματος : (m₁ + m₂) g  =  k Δl_0,σ  => Δl_0,σ = 0,4 m   συσπείρωση ελατηρίου  

k = (m₁ + m₂) ω² => 10 = 0,4 ω²  =>  ω = 5 rad/s         x_σ = 0,4 ημ(5.t + π/2)

 v_σ = 2 συν(5.t + π/2)       a_σ = - 10 ημ(5.t + π/2)    

ΣF = (m₁ + m₂) a  =>  - (m₁ + m₂) g  + F_ελατ  = (m₁ + m₂) a  =>  F_ελατ(t) = 4 - 4 ημ(5.t + π/2)      ασκείται στο συσσωμάτωμα   στο άκρο Α της ράβδου θα ασκείται αντίθετη δύναμη : F_ελατ(t)' =  - 4 + 4 ημ(5.t + π/2)  <  0    ομόρροπη του βάρους της ράβδου

ισορροπία ράβδου :  ροπές ως προς Ο :  Στ_(Ο) = 0  =>  (- Μ g) (- L/2)  +  B i L (- L/2)  + F_ελατ(t)' (- L)  =  0  =>

  =>  + 4  0,5  -  1 i 0,5  + { - 4 + 4 ημ(5.t + π/2) } (- 1)  =  0  =>

  =>  + 2  -  i 0,5  +  4  - 4 ημ(5.t + π/2)  =  0  =>  i(t) = + 12 - 8 ημ(5.t + π/2)  >  0    

  + 12 - 8 ημ(5.t + π/2)  = +12 + 8 ημ(5.t + π/2 + π)  = +12 + 8 ημ(5.t + 3π/2)  = +12 + 8 ημ(5.t - π/2)  

η ράβδος ΟΑ διαρρέεται από ένα σταθερής έντασης Ι = 12 Α  ρεύμα από πηγή συνεχούς ρεύματος ( μπαταρία )  και  από ένα εναλλασσόμενο ρεύμα  εντάσεως i = 8 ημ(5.t - π/2)  από πηγή εναλλασσομένου ρεύματος  ( στρεφόμενο πλαίσιο μέσα σε ομογενές μαγνητικό πεδίο ) 

η πηγή συνεχούς έχει τάση  V₍₌₎  =  Ι  R  =  12 Α  2 Ω  => V₍₌₎ = 24 V 

η πηγή εναλλασσομένου V_(~) = i R = 8 ημ(5.t + 3π/2)  2 Ohm  => V_(~) = 16 ημ(5.t + 3π/2) (Volt) = - dΦ / dt =>

  =>  dΦ  =  - 16 ημ(5.t + 3π/2) dt  =>   Φ(t)  = 3,2 συν(5.t + 3π/2)  - 3,2 συν(+ 3π/2)  =>

  =>  Φ(t)  = 3,2 συν(5.t + 3π/2)  => Φ(t) = 3,2 ημ(5.t) (Weber)   μαγνητική ροή που διέρχεται από το πλαίσιο,  συναρτήσει του χρόνου 

ισχύς ρεύματος :  P  =  i² R = [ 12 + 8 ημ(5.t + 3π/2) ]²  2  =  288  + 384 ημ(5.t + 3π/2)  + 128 ημ²(5.t + 3π/2) =

  =  288  + 384 ημ(5.t + 3π/2)  + 128 ημ²(5.t + 3π/2) =