(α) ροπές ως προς Α : Στ = 0 => w . L/2 - T . L = 0 => T = w/2 = 5 N
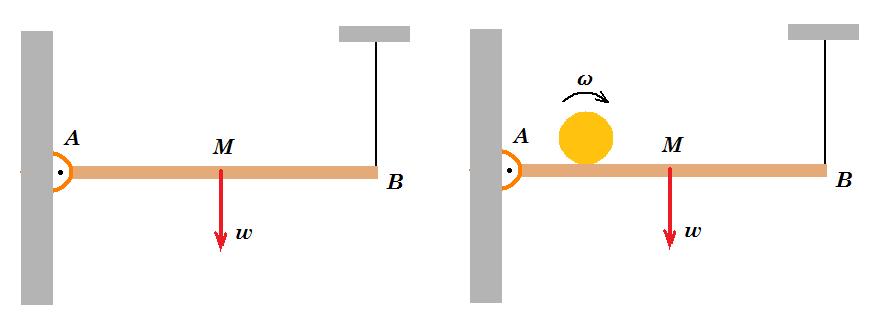
13. Η ομογενής ράβδος του σχήματος έχει βάρος w = 10 N και μήκος ℓ = 4 m. Το ένα της άκρο αρθρώνεται σε κατακόρυφο τοίχο και το άλλο της άκρο κρέμεται από κατακόρυφο σχοινί με αποτέλεσμα να ισορροπεί οριζόντια.
α) Να βρεθεί η τάση του νήματος.
β) Να βρεθεί η δύναμη που δέχεται η ράβδος από την άρθρωση.
Tη χρονική στιγμή t = 0, από το άκρο Α ξεκινάει να κυλίεται χωρίς να ολισθαίνει πάνω στη ράβδο ένας κύλινδρος βάρους w1 = 10 N με επιτάχυνση αcm = 1 m/s2 . Να υπολογίσετε :
γ) Την τάση του νήματος τη χρονική στιγμή t = √3 s.
δ) Τη γωνιακή ταχύτητα και τη θέση του κυλίνδρου, όταν η τάση του νήματος γίνει 10 Ν. (Δίνεται η ακτίνα του κυλίνδρου R = 0,1 m).
(ε) Εκφράστε την τάση του νήματος και την δύναμη που δέχεται η ράβδος από την άρθρωση συναρτήσει του χρόνου. [ α) 5N β) 5N γ) 8,75N δ) 20rad/s ] (α) ροπές ως προς Α : Στ = 0 => w . L/2 - T . L = 0 => T = w/2 = 5 N
(β) ΣF = 0 => FA + T - w = 0 => FA + 5 - 10 = 0 => FA = 5 N
(γ) κίνηση κυλίνδρου : x = 0,5 . a . t2 = 0,5 . 1 . 3 = 1,5 m < 2 m = L/2
ροπές ως προς Α : Στ = 0 => w.L/2 + w1 .x - T.L = 0 => 10 . 2 + 10 . 1,5 - T . 4 = 0 => T = 35/4 N
(δ) T = 10 N ροπές ως προς Α : Στ = 0 => w . L/2 + w1 . x - T . L = 0 =>
=> 10 . 2 + 10 . x - 10 . 4 = 0 => x = 2 m ο κύλινδρος βρίσκεται στο μέσον της ράβδου
x = 0,5 . a . t2 => 2 = 0,5 . 1 . t2 => t = 2 sec υ = α t = 1 . 2 = 2 m/s
υ = ω R => ω = υ / R = 2 / 0,1 = 20 rad/s
(ε) ροπές ως προς Α : Στ = 0 => w . L/2 + w1 . x - T . L = 0 =>
=> T . L = w . L/2 + w1 . 0,5 . a . t2 => T . 4 = 10 . 2 + 10 . 0,5 . 1 . t2 => T = 5 + 5/4. t2
ΣF = 0 => FA + T - w - w1 = 0 => FA = w + w1 - T = 10 + 10 - ( 5 + 5/4. t2 ) => FA = 15 - 5/4. t2
για x = L => 0,5 . a . t2 = L => 0,5 . 1. t2 = 4 => t2 = 8 => t = 2√2 sec
T = 5 + 5/4. t2 FA = 15 - 5/4. t2 0 < t < 2√2 sec
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
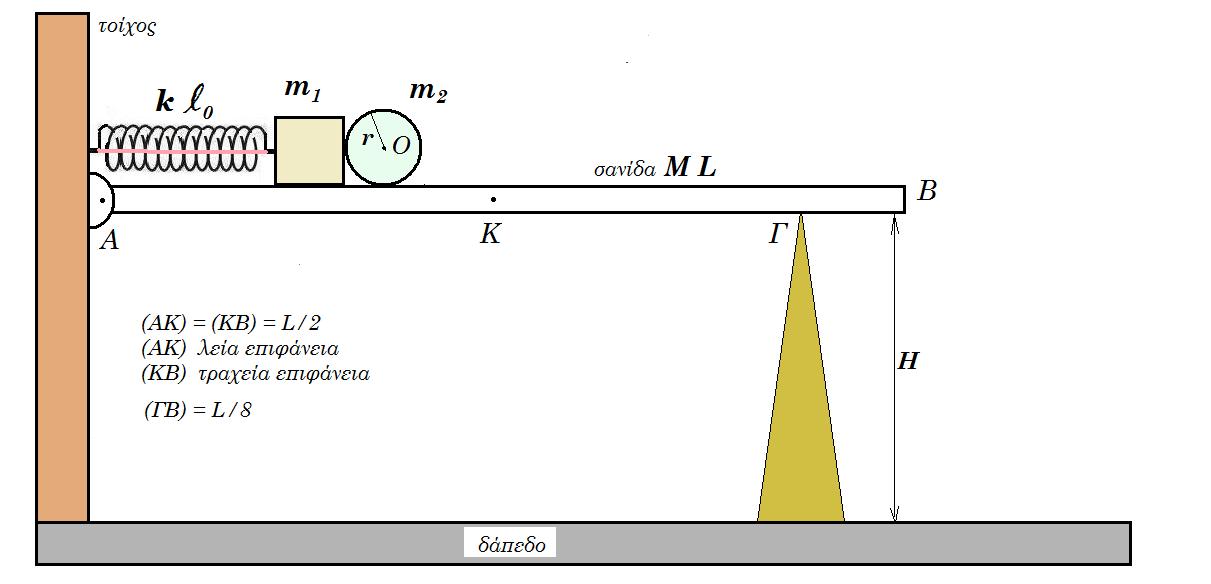
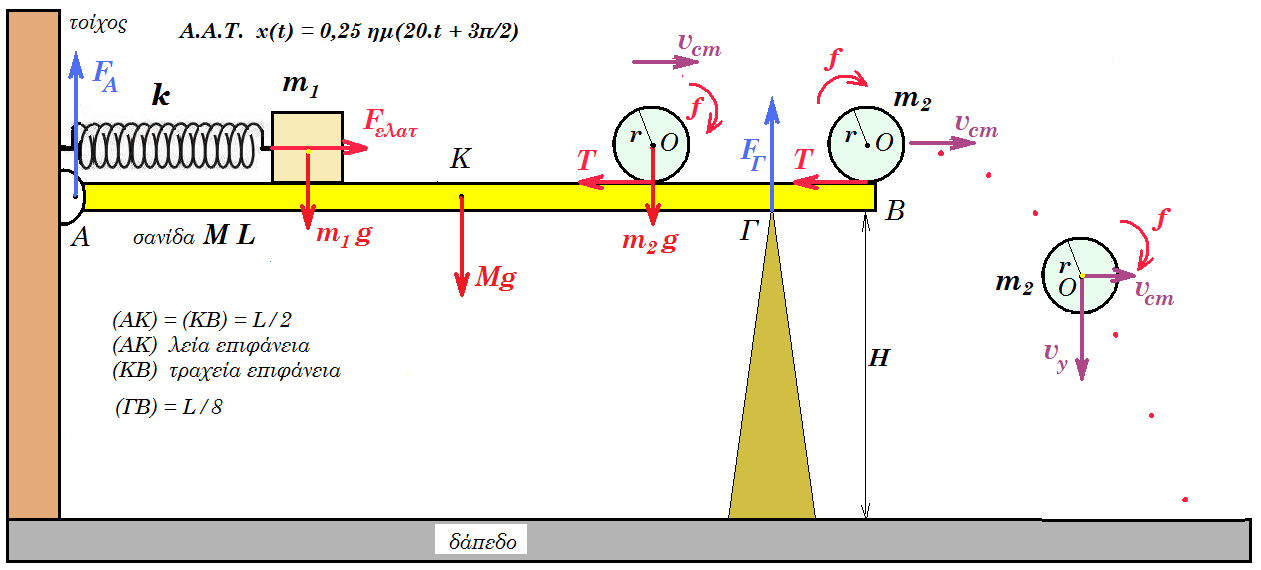
Στη διάταξη του σχήματος το ιδανικό ελατήριο σταθεράς k = 800 N/m φυσικού μήκους l0 = 0,5 m συνδέεται σε κατακόρυφο τοίχο με το ένα άκρο ενώ στο άλλο άκρο συνδέεται με σώμα Σ1 μάζας m1 = 2 kg το οποίο είναι σε επαφή με στεφάνη Σ2 μάζας m2 = 0,5 kg ακτίνας r = 0,1 m. Η λεπτή σανίδα ΑΒ έχει μάζα Μ = 4 kg μήκος L = 2 m, είναι σε οριζόντια θέση, στο άκρο Α υπάρχει άρθρωση με τον τοίχο, στο σημείο Γ υπάρχει στήριγμα (ΓΒ) = L/8. Από το άκρο της Α μέχρι το μέσον της Κ η επιφάνειά της είναι λεία ενώ από το μέσον Κ μέχρι το άκρο Β είναι τραχεία με συντελεστή μ = 0,1. Το άκρο Β της σανίδας απέχει από το δάπεδο ύψος Η = 10 m. Τα άκρα του ελατηρίου συνδέονται με λεπτό αβαρές νήμα έτσι ώστε να είναι συσπειρωμένο. Στο ελατήριο έχει αποθηκευθεί ενέργεια 25 J. Τη στιγμή t0 = 0 κόβουμε το νήμα.
(α) Μελετήστε την κίνηση των σωμάτων Σ1 και Σ2.
(β) Βρείτε την δύναμη που δέχεται η σανίδα στα σημεία Α και Γ συναρτήσει του χρόνου.
η αποθηκευμένη ενέργεια του συσπειρωμένου ελατηρίου γίνεται κινητική ενέργεια των δύο σωμάτων όταν αυτό αποκτήσει το φυσικό του μήκος
25 J = ½ k Δl2 = ½ (m1 + m2) v02
Δl2 = 2 25 J / 800 N/m = 25/400 = ( 5/20 )2 = ( 1/4 )2 => Δl = 0,25 m = 1/4 m αρχική συσπείρωση του ελατηρίου
v02 = 2 25 J / 2,5 kg = 20 => v0 = 2√5 m/s ταχύτητα των σωμάτων όταν το ελατήριο έχει το φυσικό του μήκος
τα σώματα αρχίζουν να κινούνται προς τα δεξιά το ελατήριο σπρώχνει τα σώματα με δύναμη Fελατ = k x προς τα δεξιά, όταν το ελατήριο αποκτήσει το φυσικό του μήκος τα σώματα έχουν ταχύτητα v0 = 2√5 m/s αλλά το Σ1 δέχεται από το ελατήριο δύναμη Fελατ = k x προς τα αριστερά διότι το ελατήριο επιμηκύνεται οπότε το Σ1 επιβραδύνεται ενώ το Σ2 συνεχίζει με ταχύτητα v0 = 2√5 m/s προς τα δεξιά
το Σ1 θα εκτελέσει Α.Α.Τ. με πλάτος Δl = 0,25 m συχνότητα ω2 = k / m1 = 800 / 2 => ω = 20 rad/s f = ω / 2π = 10/π Hz T = 1/f = π/10 s διότι η επιφάνεια της σανίδας είναι λεία μέχρι το μέσον της Κ
το Σ2 μέχρι το μέσον Κ της σανίδας ολισθαίνει με σταθερή ταχύτητα v0 = 2√5 m/s προς τα δεξιά ενώ από το σημείο Κ μέχρι το άκρο Β κυλίεται ω = v0 / r = 2√5 m/s / 0,1 m = 20√5 rad/s
