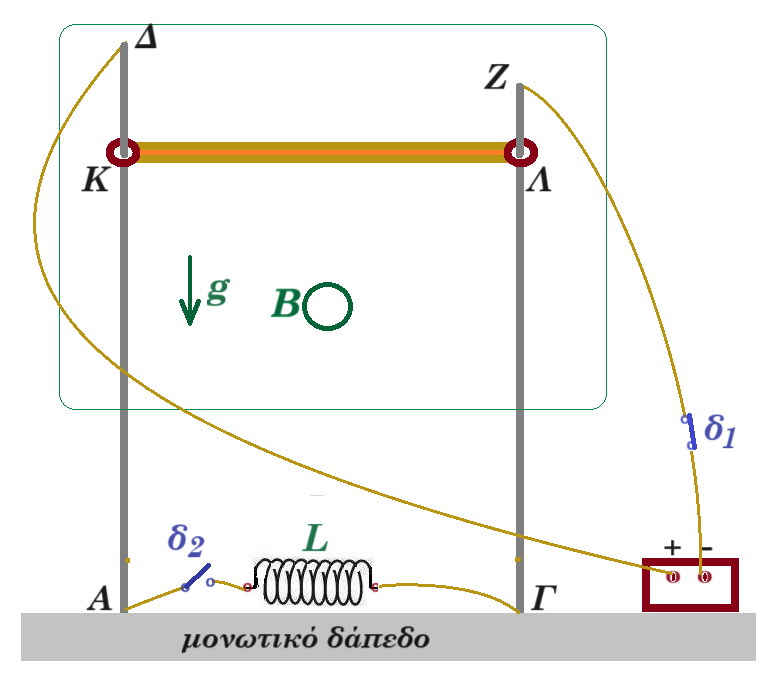
Η διάταξη του σχήματος είναι σε κατακόρυφο επίπεδο, οι κατακόρυφοι αλουμινένοι αγωγοί ΑΔ και ΓΖ συνδέονται στα σημεία Α και Γ, με λεπτά σύρματα με τα άκρα πηνίου που φέρει Ν = 1000 σπείρες  κάθε μία έχει εμβαδόν Α = π 10^-3 m² το μήκος του πηνίου είναι  l = 10 cm,  η ωμική του αντίσταση  R_π = 8 Ω.  Τα άκρα Δ και Ζ των αγωγών συνδέονται με πηγή συνεχούς ρεύματος που έχει ηλεκτρεγερτική δύναμη Ε = 24 V εσωτερική αντίσταση r = 4 Ω, με τον διακόπτη δ₁  κλειστό.  Στο χώρο υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο εντάσεως Β.  Χάλκινη ράβδος ΚΛ ισορροπεί οριζόντια (ακίνητη) μέσα στο μαγνητικό πεδίο.  Η ράβδος έχει μήκος d = 1 m  μάζα m = 0,1 kg  ωμική αντίσταση R_ΚΛ = 2 Ω. 

1.  Βρείτε την ένταση του ομογενούς μαγνητικού πεδίου (φορά, μέτρο), ο διακόπτης δ₁ είναι κλειστός ενώ ο διακόπτης δ₂ είναι ανοικτός.

Τη χρονική στιγμή  t = 0 ανοίγουμε τον διακόπτη δ₁ και ταυτόχρονα  κλείνουμε τον δ₂.

2.   Μελετήστε την κίνηση της ράβδου.  

1.     E = i (r + R_ΚΛ)  =>  24 V = i (4 Ω + 2 Ω) => i = 4 A  

  m g = B i d  =>  0,1 kg  10 m/s²  =  B  4 A  1 m  =>  B = 0,25 T   οριζόντια προς τα μέσα 

2.   η ράβδος κινειται προς τα κάτω κατακόρυφα  τα ηλεκτρόνιά της δέχονται δύναμη Lorentz  με συνέπεια να κινούνται προς το άκρο Κ  το οποίο φορτίζεται αρνητικά  οπότε το άκρο Λ φορτίζεται θετικά  με συνέπεια  να δημιουργηθεί στα άκρα επαγωγική τάση  Ε_επαγ = Β d v = 0,25 T  1 m  v = v/4   οπότε το κύκλωμα  ράβδος - πηνίο  να διαρρέεται από ρεύμα  οπότε το πηνίο αντιδρά  και  στα άκρα εμφανίζεται τάση αυτεπαγωγής  Ε_αυτ = - L di/dt       

  L = 4π 10^-7 Ν² Α / l = 4π 10^-7 10⁶  π 10^-3 / 10^-1  =  4π² 10^-3 Ηenry =  0,04 Henry

 νόμος του  Ohm για κλειστό κύκλωμα :  Ε_επαγ + Ε_αυτ =  i ( R_ΚΛ + R_π )  =>  0,25 υ - L di/dt =  i (2 + 8)  =>  0,25 υ -  0,04 di/dt =  10 i      (1)

   m g  -  B l i  =  m a  =  m dv/dt  =>  1 - 0,25 i  =  0,1 dv/dt  =>  i = 4  -  0,4 dv/dt    (2)  

(2) =>  di/dt  =  - 0,4  d²v/dt²     (3)  

(1) , (2) , (3) =>  0,25 v  -  0,04 ( - 0,4 d²v/dt² ) = 10 ( 4  -  0,4 dv/dt )  =>  

    =>  0,25 v   +  0,016  d²v/dt²  =  40  -  4 dv/dt   =>  

    =>  0,016  d²v/dt²  +  4 dv/dt   +  0,25 v  -  40  =  0      (4)

το χαρακτηριστικό πολυώνυμο είναι :   0,016  ρ²  +  4 ρ   +  0,25  =  0     

   Δ = 16 - 0,016 = 16         ρ_1,2  =  (- 4  ±  4) / 0,032  =   0    ή    - 250    

 v  =  A e ^{-250 t}  +  C       dv/dt  =  -250 A e ^{-250 t}      d²v/dt² = + 62500 A e ^{-250 t}       

αρχικά  t = 0   υ = 0   οπότε  A + C = 0  =>  C = -A      

            α = g = 10 m/s²    οπότε  -250 A = 10  =>  A = - 25

   v  =  -25 e ^{-250 t}  + 25         dv/dt  =  6250 e ^{-250 t}      d²v/dt² = - 15.625.000 e ^{-250 t} 

(4) =>  0,016 ( - 15.625.000 e ^{-250 t} )  +  4  6250 e ^{-250 t}  +  0,25 ( -25 e ^{-250 t} + 25 ) - 40 = 0  =>

  =>  - 250.000 e ^{-250 t}  + 25.000 e ^{-250 t}  -  6,25 e ^{-250 t}  + 6,25  -  40  =  0   =>