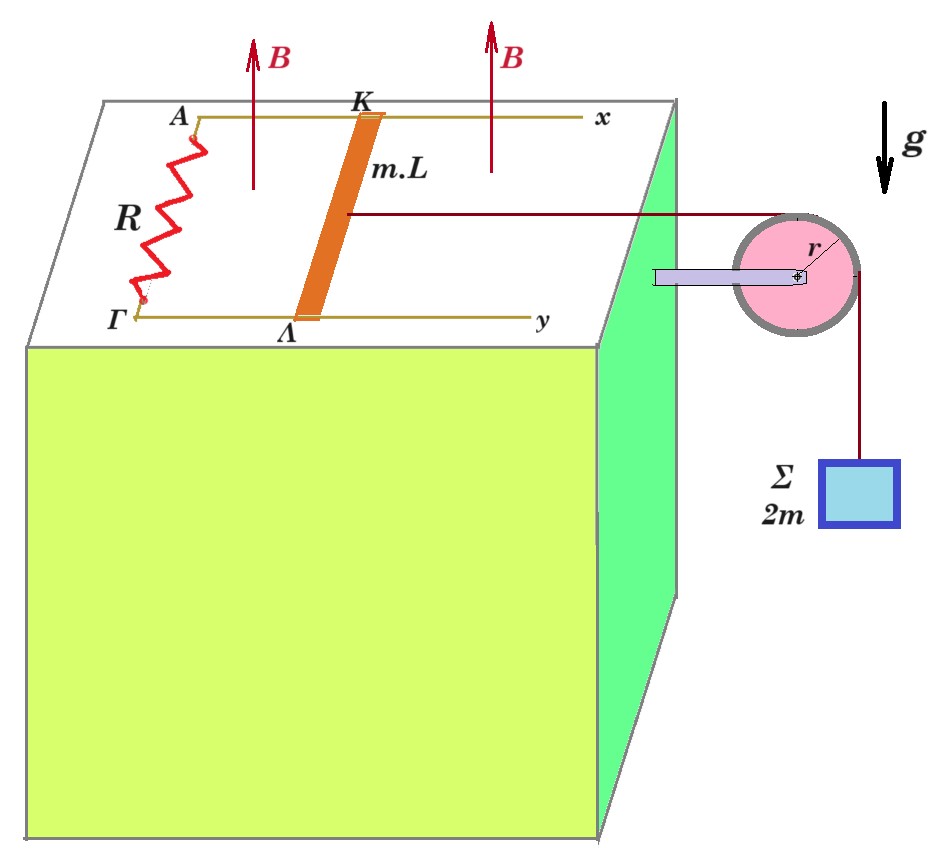
Πάνω σε μονωτικό τραπέζι, μεγάλου μήκους, βρίσκονται δύο παράλληλοι οριζόντιοι αγωγοί Αx και Γy  αμελητέας ωμικής αντίστασης, που απέχουν μεταξύ τους απόσταση L. Τα άκρα Α και Γ συνδέονται με αντίσταση R. Κατά μήκος των δύο αγωγών και κάθετα στην κατεύθυνσή τους, μπορεί να ολισθαίνει χωρίς τριβές και παραμένοντας σε επαφή με αυτούς, μεταλλική αγώγιμη ράβδος ΚΛ, μήκους L, μάζας m₁=m και αμελητέας ωμικής αντίστασης. Στο μέσο της μεταλλικής ράβδου ΚΛ είναι δεμένο οριζόντιο αβαρές και μη εκτατό νήμα. Το νήμα διέρχεται μέσα από τροχαλία αμελητέας μάζας και το άλλο άκρο του είναι δεμένο με σώμα Σ μάζας m₂=2m το οποίο κρέμεται κατακόρυφα. Όλο το σύστημα βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο έντασης 𝛣⃑ με φορά προς τα πάνω, όπως φαίνεται στο σχήμα. Αρχικά κρατάμε το σύστημα ακίνητο. Τη χρονική στιγμή t0=0 αφήνουμε το σύστημα ελεύθερο να κινηθεί, και τη χρονική στιγμή t2 τα σώματα θα αρχίσουν να κινούνται με σταθερή ταχύτητα υορ. Αν α₀ είναι η επιτάχυνση της ράβδου ΚΛ τη χρονική στιγμή t₀ =0, και α₁ είναι η επιτάχυνση της ράβδου ΚΛ τη χρονική στιγμή t₁ που η ταχύτητα της ράβδου είναι η μισή της τελικής σταθερής ταχύτητάς της υ_ορ, (υ₁=υ_ορ/2), τότε ισχύει:            

α)  α₀/α₁ = 2        β)  α₀/α₁ = 3         γ)  α₀/ α₁ = 6

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

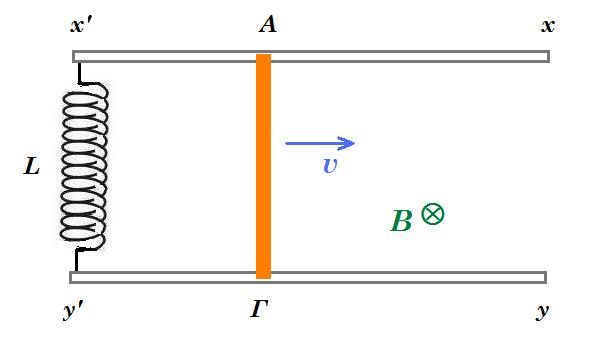
Ο αγωγός ΑΓ, μήκους l=1m, μάζας m=2kg ωμικής αντίστασης R=4Ω ισορροπεί οριζόντια σε επαφή με δύο ευθύγραμμους αγωγούς x'x και y'y, οι οποίοι δεν παρουσιάζουν αντίσταση και απέχουν κατά l, ενώ στα άκρα τους x΄και y΄ συνδέεται ένα ιδανικό πηνίο, με συντελεστή αυτεπαγωγής L=0,2 Η. Το όλον σύστημα βρίσκεται μέσα σε ένα κατακόρυφο ομογενές μαγνητικό πεδίο έντασης Β=1Τ, όπως στο σχήμα.  Τη χρονική στιγμή t₀=0  δίνουμε οριζόντια ταχύτητα υ₀ στον αγωγό οπότε αυτός κινείται σε επαφή με τους δύο αγωγούς x'x και y'y.  Μια χρονική στιγμή t₁, ο αγωγός ΑΓ έχει ταχύτητα υ₁=2m/s, με φορά προς τα δεξιά, ενώ η τάση στα άκρα του είναι ίση με V_ΑΓ=0,4V. Για την στιγμή αυτή ζητούνται:

α)   Η ένταση του ρεύματος που διαρρέει το κύκλωμα, καθώς και ο ρυθμός μεταβολής της έντασης του ρεύματος  di/dt.

β)   Ο ρυθμός μεταβολής της κινητικής ενέργειας του αγωγού ΑΓ. Ποια η αντίστοιχη ηλεκτρική ισχύς του ρεύματος που διαρρέει το κύκλωμα;

γ)   Η ενέργεια του μαγνητικού πεδίου του πηνίου, καθώς και ο ρυθμός μεταβολής της ενέργειας αυτής.

 ΘΕΜΑ Δ 
Η διπλή τροχαλία του σχήματος με ακτίνες  r₁ = 0,05 m και r₂ = 2r₁, μπορεί να στρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα περιστροφής, που διέρχεται από το κέντρο της.   Η τροχαλία έχει αμελητέα μάζα, δηλαδή κάθε στιγμή ισχύει για αυτήν ότι το άθροισμα των ροπών που της ασκούνται ως προς τον άξονα περιστροφής της είναι ίσο με μηδέν,  είτε ισορροπεί, είτε περιστρέφεται.   Γύρω από το εξωτερικό αυλάκι της τροχαλίας υπάρχει τυλιγμένο αβαρές και μη εκτατό νήμα, στο άκρο του οποίου είναι δεμένο ένα σώμα Σ₂ μάζας  m₂ = 0,5 kg. Στο εσωτερικό αυλάκι της τροχαλίας είναι επίσης τυλιγμένο αβαρές και μη εκτατό νήμα, το άκρο του οποίου είναι δεμένο στο μέσο ομογενούς  μεταλλικής ράβδου ΚΛ, μήκους  L = 1 m, αντίστασης R₃ και μάζας m₁ = 0,2 kg,  η οποία μπορεί να κινείται πάνω στους οριζόντιους, αγώγιμους – αμελητέας αντίστασης - οδηγούς Αx και Γx’.   Ο συντελεστής οριακής στατικής τριβής μεταξύ των οδηγών και της ράβδου ΚΛ έχει τιμή μ_s = 0,5 και είναι ίσος με το συντελεστή τριβής ολίσθησης  (μ_s=μ_ολ). 
Στο χώρο υπάρχει κατακόρυφο ομογενές μαγνητικό πεδίο έντασης μέτρου  Β = 2 T  με τη φορά των δυναμικών γραμμών προς τα κάτω.  Τα σημεία του κυκλώματος Α, Γ  συνδέονται μέσω του μεταγωγού δ, είτε με ηλεκτρική πηγή ΗΕΔ Ε = 9 V  και εσωτερικής αντίστασης R₁ = 1 Ω, είτε με αντίσταση R₂ = 1 Ω.   Στην αρχή ο μεταγωγός δ βρίσκεται στη θέση Ζ και η ράβδος ισορροπεί με την τριβή να έχει φορά προς τα αριστερά και μέτρο ίσο με το μέτρο της οριακής τριβής.

Δ1.   Να υπολογίσετε την αντίσταση R₃ της μεταλλικής ράβδου ΚΛ.

Την χρονική στιγμή t=0s φέρνουμε τον μεταγωγό δ στη θέση Ε και η ράβδος αρχίζει να κινείται πάνω στους οδηγούς.         Μελετήστε την κίνηση ράβδου  και  σώματος Σ₂  
Δ2.   Υπολογίστε την τάση στα άκρα του αντιστάτη R₂ την χρονική στιγμή που το σώμα Σ₂ κατέρχεται με επιτάχυνση α₂=2m/s²

Δ3.   Να υπολογίσετε την μέγιστη – οριακή – ταχύτητα υ_ορ που θα αποκτήσει το σώμα Σ₂.

Δ4.   Για το χρονικό διάστημα που απαιτείται για να κάνει η τροχαλία 9 στροφές μετά από την χρονική στιγμή που το σώμα Σ₂ αποκτά την μέγιστη – οριακή – ταχύτητα, να υπολογίσετε τη μείωση της δυναμικής ενέργειας του σώματος Σ₂ και να επιβεβαιώσετε την ισχύ της αρχής διατήρησης της ενέργειας.      Δίνεται g=10 m/s²  

Δ1.    ο μεταγωγέας  δ  είναι στη θέση Ζ :    

η ράβδος διαρρέεται από ρεύμα  i = E / (R₁ + R₃)  (1)   και είναι μέσα σε ομογενές μαγνητικό πεδίο Β  άρα δέχεται δύναμη Laplace  F_L = B . i . l  (2)   

    ισορροπία ράβδου   ΣF = 0  => Τ₁ - F_L - T_τρ = 0   => Τ₁ - F_L -  μ_s . m₁ . g  = 0   (3)     

    ισορροπία  Σ₂   m₂ . g = T₂  =>  0,5 . 10 = T₂  =>  T₂ = 5 N   (4)       

    ισορροπία τροχαλίας  ( ροπές )  T₁ . r₁ = T₂ . r₂  =>  T₁ . r₁ = 5 N . 2.r₁ =>  T₁ = 10 N  (5)  

  (3), (4), (5)  =>  10 - F_L -  0,5 . 0,2 . 10  = 0  =>  F_L = 9 N  (6)   

       (2), (6)  =>  9 N = 2 T . i . 1 m  =>  i = 4,5 A        

   η  (1)  =>  R₁ + R₃  =  E / i  =>  R₃  =  E / i  - R₁ =  9 / 4,5  -  1  =>  R₃ = 1 Ω     

                μελέτη της κίνησης  ράβδου και σώματος Σ₂   

 σώμα Σ₂ :  ΣF = m₂ α₂  =>  m₂ g  - Τ₂  =  m₂ α₂  => Τ₂  =  0,5 10  -  0,5 α₂ =>  Τ₂ = 5 - 0,5.α₂  (1)   

 τροχαλία  ( ροπές )   T₁ . r₁  =  T₂ . r₂  =>   T₁ . r₁  =  Τ₂ . 2.r₁  =>  T₁ = 2 Τ₂   (2) 

 ράβδος :  ΣF = m₁ α₁  =>  Τ₁ - F_L - T_τρ = m₁ α₁  =>   Τ₁  -  Β i l  -  μ_s m₁ g  = m₁ α₁  =>

              =>   Τ₁  =  2 . i . 1  +  0,5 . 0,2 . 10  +  0,2 . α₁ =>   Τ₁  =  2.i  +  1  +  0,2 . α₁   (3) 

νόμος του Ohm : Ε_επαγ = i (R₂ +R₃) => Β υ₁ l  =  i  (R₂ +R₃)  => 2 υ₁ 1 = i (1+1)  =>  υ₁ = i 

        επειδή  r₂ = 2.r₁    τότε  υ₂ = 2.υ₁  =>  α₂ = 2.α₁    

(3) =>^(2),(1)  Τ₁  =  2.i  +  1  +  0,2 . α₁  =>   2. ( 5 - 0,5.α₂ )  =  2.i  +  1  +  0,2 . α₁ => 

    =>  10 - 2α₁ =  2.υ₁  +  1  +  0,2 . α₁  =>  -2,2.α₁  =  2.υ₁ -  9  =>  α₁  =  -10/11.υ₁ +  45/11     

η ράβδος κινείται η ταχύτητάς της αυξάνεται οπότε η επιτάχυνσή της ελαττώνεται  και  κάποια στιγμή θα μηδενισθεί οπότε η ράβδος θα αποκτήσει σταθερή ταχύτητα υ_ορ = 45/11 ^. 11/10 = 4,5 m/s 

μαθηματική ανάλυση :

 dv/dt = -10/11 v + 45/11  =>  dv/dt = -10/11 ( v - 4,5 ) =>  dv /(v - 4,5) = -10/11 dt  =>

  =>   ln [ (v - 4,5) / (- 4,5) ]  =  -10/11 t  =>   v - 4,5  =  - 4,5 e^{-10/11 . t}   =>

 =>   v(t)  =  4,5 ( 1 - e^{-10/11 . t} )      v(0) = 0

   a = dv/dt  =>  a(t)  =  45/11 e^{-10/11 . t}       a(0) = 45/11 m/s²   αρχική επιτάχυνση ράβδου ΚΛ  

 i(t) = v(t)  = 4,5 ( 1 - e^{-10/11 . t} )     i(0) = 0      

 F_L(t)  = B l i =  2  1  4,5 ( 1 - e^{-10/11 . t} ) =>  F_L(t) = 9 ( 1 - e^{-10/11 . t} )    F_L(0) = 0  

 Τ₂  =  5 - 0,5.α₂  = 5 - 0,5 . 2 . 45/11 e^{-10/11 . t}  => Τ₂ = 5 - 45/11 e^-10/11.t 

 T₁ = 2 Τ₂  =>  Τ₁ = 2 ( 5  -  45/11 e^{-10/11 . t} )  => Τ₁ = 10 - 90/11 e^{-10/11 t}   

            T₁(0)  =  10  - 90/11 = 20/11 N   

 P_R = i² (R₃ + R₂)  = 4,5² ( 1 - e^{-10/11 . t} )²  2  =>  P(t)  =  9  4,5 ( 1 - e^{-10/11 . t} )²     

 P_FL  =  F_L v  =  9 ( 1 - e^{-10/11 . t} )   4,5 ( 1 - e^{-10/11 . t} )  =  9  4,5 ( 1 - e^{-10/11 . t} )²    

 P_Tτρ  =  Τ_τρ υ  =  μ_s  m₁  g  4,5 ( 1 - e^{-10/11 . t} )  =  0,5  0,2  10  4,5 ( 1 - e^{-10/11 . t} )  =>

         =>   P_Tτρ(t) =  4,5 ( 1 - e^{-10/11 . t} )  

 dK/dt =  m₁  v  a  =  0,2   4,5 ( 1 - e^{-10/11 . t} )   45/11 e^{-10/11 . t}   =>

              =>   dK/dt  =  4,5  9/11 e^{-10/11 . t}  ( 1 - e^{-10/11 . t} )   

 P_T1  =  Τ₁ υ  =  [ 10  -  90/11 e^{-10/11 . t} ]  4,5 ( 1 - e^{-10/11 . t} )  =>  

            =>    Ρ_Τ1  =   45  [ 1  -  9/11 e^{-10/11 . t} ]  ( 1 - e^{-10/11 . t} )     

η ράβδος ΚΛ κινείται λόγω της τάσης νήματος Τ₁ , που έχει διπλάσιο μέτρο από την τάση νήματος Τ₂  η οποία ασκείται στο σώμα Σ₂ ,   υπάρχει δύναμη τριβής ,  δύναμη Laplace  οι οποίες είναι αντίρροπες της Τ₁  και  η ράβδος έχει ταχύτητα   

P_FL  + P_Tτρ  +  dK/dt  = 

  =  9 4,5 ( 1 - e^{-10/11 . t} )²  +  4,5 ( 1 - e^{-10/11 . t} )  + 4,5  9/11 e^{-10/11 . t}  ( 1 - e^{-10/11 . t} )   =  

  =  4,5 ( 1 - e^{-10/11 . t} )   [  9 ( 1 - e^{-10/11 . t} )  +  1  +  9/11 e^{-10/11 . t}  ]  =    

  =  4,5 ( 1 - e^{-10/11 . t} )   [  10 -  9 e^{-10/11 . t}  +  9/11 e^{-10/11 . t}  ]  =

  =  4,5 ( 1 - e^{-10/11 . t} )   [  10 -  90/11 e^{-10/11 . t}  ]  =  P_T1      

Δ2.    ο μεταγωγέας  δ  είναι στη θέση Ε :

  ΣF = m₂ α₂   =>   m₂ g  -  Τ₂  =  m₂ α₂  =>   0,5 10  -  Τ₂  =  0,5 2  => Τ₂  =  4 Ν     

  T₁ . r₁  =  T₂ . r₂  =>  T₁ . r₁  =  4 N . 2.r₁  =>  T₁  =  8 N   

 η ράβδος κινείται  μέσα σε μαγνητικό πεδίο  κάθετα στις δυναμικές γραμμές,   στα ηλεκτρόνια της ράβδου ασκούνται δυνάμεις Lorenz  με συνέπεια να μετακινούνται προς το άκρο Κ    το οποίο φορτίζεται αρνητικά (-)  οπότε το άκρο Λ φορτίζεται θετικά (+),  έτσι η ράβδος γίνεται πηγή ηλεκτρικού ρεύματος,  στα άκρα ΚΛ εμφανίζεται επαγωγική τάση Ε_επαγ = Β . υ₁ . l        

  νόμος του Ohm  για κλειστό κύκλωμα :  Ε_επαγ =  i (R₂ +R₃)  =>  Β υ₁ l  =  i (R₂ +R₃)      

  η τροχαλία περιστρέφεται με γωνιακή ταχύτητα  ω = α_γων .t   τότε  υ₁ = ω . r₁  &  υ₂ = ω . r₂    επειδή   r₂ = 2.r₁  τότε  υ₂ = 2.υ₁ => α₂ = 2.α₁   ( επιταχύνσεις )   άρα  α₁ = 1 m/s²   

  η ράβδος δέχεται δύναμη  Laplace  F_L = B . i . l    &  τάση νήματος  Τ₁ = 8 Ν 

  δύναμη τριβής :   ΣF = Τ₁ - F_L - T_τρ =  m₁ α₁  =>  8  - F_L -  0,5 0,2 10  =  0,2 1 =>  F_L = 6,8 Ν 

 από τη σχέση    F_L = B i l =>   6,8 Ν  = 2 Τ  i  1 m  =>  i  =  3,4 A       

  η τάση στα άκρα της R₂  :  V₂  =  V_ΓΕ  =  3,4 Α  1 Ω  =>    V_ΓΕ  =  3,4 Volt    

 από τη σχέση    Β υ₁ l  =  i (R₂ +R₃)   =>  υ₁  =  3,4 (1 + 1) / 2.1  =>  υ₁ = 3,4 m/s       

Δ3.   σώμα Σ₂ :   ΣF = 0  =>  Τ₂ - m₂ g = 0  =>  Τ₂  = 5 Ν                

        τροχαλία  ( ροπές )   T₁ . r₁  =  T₂ . r₂  =>   T₁ r₁  =  5 N  2.r₁  => T₁ = 10 N 

ράβδος :  ΣF = 0  =>  Τ₁ - F_L - T_τρ = 0 =>  Τ₁  -  Β i l  -  μ_s m₁ g  = 0  => 10  -  2 i 1 -  0,5 0,2 10 = 0 =>

                              =>   i  =  4,5 A    

νόμος Ohm : Ε_επαγ =  i (R₂ +R₃)  =>  Β  υ_ορ l  =  i (R₂ +R₃)  =>  2 υ_ορ 1 =  4,5 .(1+1) => υ_ορ = 4,5 m/s  

επειδή  r₂ = 2.r₁    τότε  υ₂ = 2.υ_ορ = 9 m/s      το Σ₂ θα κινείται με οριακή ταχύτητα   υ_ορ(2)  =  9 m/s  

Δ4.  η τροχαλία κάνει  Ν = 9 περιστροφές   τότε  θ = Ν 2π rad  =  18π rad      

  υ_ορ(2)  =  ω  r₂  =>  ω = 9 m/s / 0,1 m =>  ω = 90 rad/s       ω = θ / t  =>  t = 18π / 90  =>  t = 0,2.π s 

  η ράβδος διανύει διάστημα   x₁  =  υ_ορ  t  =  4,5 m/s  0,2.π s  =>  x₁ = 0,9.π m          

το σώμα Σ₂  διανύει διάστημα   x₂  =  υ_ορ(2)  t  =  9 m/s  0,2.π s  =>   x₂ = 1,8.π m = h 

  U_(Σ2)  =  m₂  g  h  =  0,5 kg 10 m/s²  1,8.π m  =>   U_(Σ2) = 9.π Joule = T₂  x₂ = W_T2        

  W_T1  =  T₁  x₁  =  10 N  0,9.π m  =>   W_T1 = 9.π Joule   

  W_Tτρ  =  T_τρ x₁  =  μ_s m₁ g x₁  =  0,5  0,2 10  0,9.π  =>   W_Tτρ = 0,9.π Joule    

  F_L = B i l =  2 Τ 4,5 Α 1 m = 9 N       W_FL = F_L x₁ =  9 N 0,9.π m  =>  W_FL = 8,1.π Joule 

  Q_θερμ =  i² (R₂ + R₃)  t  =>  Q_θερμ =  4,5² (1 + 1)  0,2.π  =>   Q_θερμ = 8,1.π Joule 

παρατηρούμε ότι καθώς κατεβαίνει το σώμα Σ₂ η δυναμική βαρυτική ενέργεια μειώνεται κατά 9π J     η ράβδος κερδίζει ενέργεια 9.π J λόγω το έργου που παράγει η τάση του νήματος        η οποία ενέργεια καταναλώνεται στις τριβές 0,9.π J    και  στην δύναμη Laplace 8,1.π J     η οποία ισούται με την θερμότητα λόγω φαινομένου Joule πάνω στις αντιστάσεις R₂  και R₃   

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~`

2mg - T = 2ma               T - Bil = ma                  Bvl = iR => i = Blv/R

2mg - Bil = 3ma  =>  2mg -  B² l² v/R = 3m dv/dt ⁽¹⁾

παρατηρούμε ότι το μέτρο της επιτάχυνση μειώνεται με τον χρόνο ενώ η ταχύτητα της ράβδου αυξάνεται   μετά από πολύ χρόνο  η επιτάχυνση μηδενίζεται και η ταχύτητα αποκτά οριακή τιμή   η (1)  =>  2mg -  B² l² v_ορ /R = 0  =>  υ_ορ = 2mRg/B²l²    

 για  υ = υ_ορ/2 = mRg/B²l²   η (1) =>  2mg -  B²l²/R  mRg/B²l² = 3m α₁  =>  2mg -  mg = 3m α₁  =>  α₁ = g/3            αρχικά  υ = 0   i = 0   οπότε η  2mg - Bil = 3m a₀  => 2mg - 0 = 3m a₀  =>  α₀ = 2g/3   οπότε    α₀ / α₁ = 2            

            μαθηματικά

  (1)  =>   2g -  B²l² v/mR =  3 dv/dt  =>

=>  - B²l²/mR  ( v  -  2mRg / B²l² )  =  3 dv/dt  =>

=>  dv / ( v  -  2mRg / B²l² )  =  - B²l²/3mR dt   =>

=>  ln [ ( v  -  2mRg / B²l² ) / ( - 2mRg / B²l² ) ]  =  - B²l²/3mR dt   =>

=>  v(t)  = 2mRg/B²l²  ( 1 - e^{-B2l2/3mR dt} )                a(t)  =  2g/3 e^{-B2l2/3mR dt}      

t=0  v=0   a₀ = 2g/3        t®¥   a=0    v_ορ = 2mRg/B²l²         v₁ = v_ορ/2 = mRg/B²l²       

2mg -  B²l² v₁ /R = 3m a₁  =>  2mg  -  B²l²/R  mRg/B²l²  = 3m a₁  => 

=>  2mg  -  mg  = 3m a₁  =>   mg  = 3m a₁  => a₁ = g/3               α₀ / α₁ = 2    

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

α)  Β l v  -  L di/dt  =  i R  =>   Β l v  -  i R  =  L di/dt  =>  V_ΑΓ  = L di/dt  => 0,4 V =  0,2 H di/dt  =>  di/dt = 2 A/s  

   Β l v  -  L di/dt  =  i R  =>   1  1  2  -   0,2  2  =  i  4  =>  i = 0,4 A   

β)   dK/dt  =  m v a  =  m  v  F_L/m  =  v  F_L  =  v  B l i  =  2  1  1  0,4  =  0,8 J/s  

  P  =  i²  R  =  0,4²  4  =  0,64 Watt  

γ)  U_L  =  0,5  L  i²  =  0,5  0,2  0,4²  =  0,016 J            dU_L /dt  =  L  i  di/dt  =  0,2  0,4  2  =  0,16 J/s   

                0,16 J/s  +  0,64 Watt  =  0,8 J/s