Επαγωγή - Αυτεπαγωγή
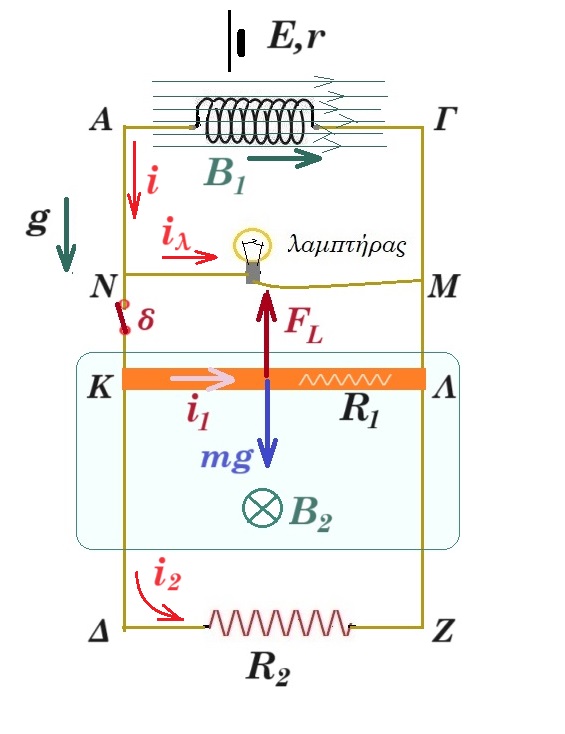
Το σωληνοειδές του σχήματος έχει μήκος l_Σ = 0,2 m, αντίσταση R_L = 1Ω και αποτελείται από Ν = 1000 σπείρες με εμβαδόν Α = π.10^ˉ2 η κάθε μια. Τα άκρα του σωληνοειδούς συνδέονται στα πάνω άκρα Α και Γ δυο κατακόρυφων μεταλλικών στύλων ΑΔ και ΓΖ, οι οποίοι απέχουν μεταξύ τους απόσταση l = 1 m, έχουν μεγάλο μήκος και αμελητέα ωμική αντίσταση. Τα άκρα Δ, Ζ συνδέονται μέσω αντιστάτη αντίστασης R₂ = 4Ω. Το σωληνοειδές βρίσκεται μέσα σε μεταβαλλόμενο, με σταθερο ρυθμό, ομογενές μαγνητικό πεδίο Β₁, με τον άξονα του παράλληλο προς τις μαγνητικές γραμμές του, όπως φαίνεται στο σχήμα. Τα μέσα των ΑΔ και ΓΖ αντίστοιχα είναι τα σημεία Ν και Μ αντίστοιχα και ενώνονται μέσω λαμπτήρα με στοιχεία κανονικής λειτουργίας P_κ = 12,5 W και V_κ = 5 V ο οποίος βρίσκεται εκτός του μαγνητικού πεδίου που μεταβάλλεται.
Ο οριζόντιος αγωγός ΚΛ που έχει μάζα m, μήκος l = 1 m και αντίσταση R₁ = 4Ω, έχει τα άκρα του Κ, Λ πάνω στους στύλους ΑΔ και ΓΖ και μπορεί να γλιστρά σε συνεχή και αγώγιμη επαφή με αυτούς, χωρίς τριβές. Ο αγωγός ΚΛ βρίσκεται σε περιοχή που υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης Β₂ = 1 Τ, όπως φαίνεται στο σχήμα. Μεταξύ των σημείων Ν και Κ υπάρχει διακόπτης δ.    g = 10 m/s²  μ₀ = 4π.10^ˉ7 Ν/A² .   Ο λαμπτήρας δεν καταστρέφεται.
Α.  Αρχικά ο διακόπτης είναι κλειστός, ο αγωγός ΚΛ ισορροπεί ακίνητος και ο λαμπτήρας λειτουργεί κανονικά. Να υπολογίσετε :
Α1)  την μάζα του αγωγού ΚΛ.
Α2)  τον ρυθμό με τον οποίο μεταβάλλεται η ένταση του μαγνητικού πεδίου Β₁, μέσα στο οποίο βρίσκεται το σωληνοειδές.
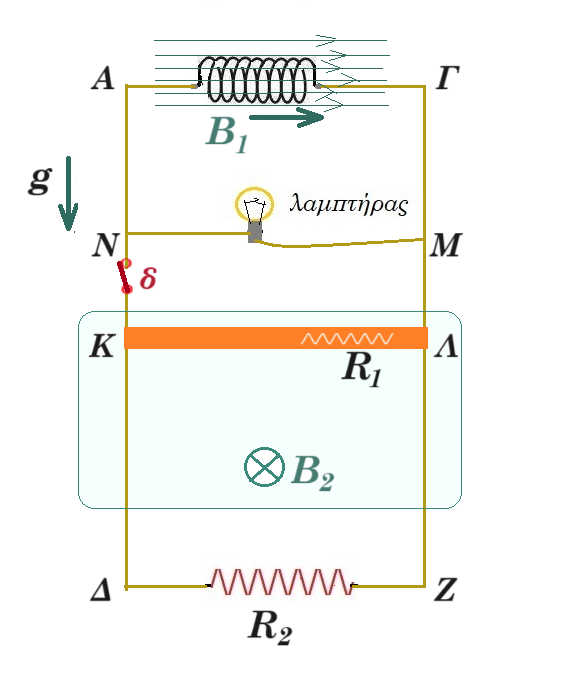
Β.  Την χρονική στιγμή t = 0 ανοίγουμε τον διακόπτη δ και ταυτόχρονα καταργούμε το μεταβαλλόμενο μαγνητικό πεδίο Β₁.
Β1)  Να ελέγξετε αν ο λαμπτήρας (έστω και στιγμιαία) θα φωτοβολήσει εντονότερα ή όχι.
Β2)  Να υπολογίσετε τον ρυθμό μεταβολής του ρεύματος που διαρρέει το σωληνοειδές την χρονική στιγμή που ο λαμπτήρας θα λειτουργήσει και πάλι κανονικά.
Β3)  Να υπολογίσετε το μέτρο της οριακής ταχύτητας του αγωγού ΚΛ.
Β4)  Να υπολογίσετε τoν ρυθμό μεταβολής της έντασης του ρεύματος που διαρρέει τον αντιστάτη R₂ όταν η ισχύς που καταναλώνει είναι P_R2 = 4 W.

Α.   i_λ  =  12,5 W / 5 V  =>  i_λ = 2,5 A           R_λ = 5 V / 2,5 Α = 2 Ω       

 1 / R_{εξωτερ.} =  1/2  +  1/4  +  1/4  =  1  =>  R_{εξωτερ.} =  1 Ω        R_ολική  =  1 + 1 = 2 Ω 

     V_NM = 5 V  =  V_ΚΛ  =  V_ΔΖ  =  V_πολική  =  Ε  -  i R_L   

  5 V  =  V_ΚΛ  =  i_ΚΛ R₁  =>  5 = i_ΚΛ 4  =>  i_ΚΛ = 1,25 Α        i₂ = 5 / 4 = 1,25 A   

        i = 2,5 + 1,25 + 1,25 = 5 A  ρεύμα που δίνει το πηνίο στο κύκλωμα

  L  =  4π 10^-7  Ν² Α / l_Σ  =   4π 10^-7  1000² π 10^-2 / 0,2  =   0,2 Henry

Ε_επαγ  = - N ΔΦ/Δt  = - N A dB₁/dt  =  i  R_ολική  =>  - 1000  π 10^-2  dB₁/dt  =  5  2   =>  dB₁/dt = - 1/π  Τ/s    

  ισορροπία ράβδου ΚΛ :   mg - B₂ l i_ΚΛ = 0   =>  m 10  =  1  1  1,25  =>  m = 0,125 kg 

Β.   

ο λαμτήρας αρχικά διαρρεόταν από 2,5Α  και όταν ανοίγει ο διακόπτης από  5Α  από το πηνίο  φωτοβολεί εντονότερα

 - L di/dt  =  i (R_L + R_λ)  =>  - 0,2 H  di/dt  =  2,5 A (1Ω + 2Ω)  =>  di/dt  =  - 2,5  3 / 0,2  A/s  => di/dt = - 37,5 A/s 

η ράβδος ΚΛ κατέρχεται    τα ηλεκτρόνιά της δέχονται δύναμη Lorentz  και συσσωρεύονται στο άκρο Κ  που φορτίζεται αρνητικά  ενώ το άκρο Λ φορτίζεται θετικά  αναπτύσσεται στα Κ, Λ τάση από επαγωγή  Ε_επαγ  =  Β₂ l v   η ράβδος διαρρέεται από ρεύμα  i   ομόρροπο του αρχικού  και η αντίσταση R₂  διαρρέεται από ρεύμα  i   αντίρροπο του αρχικού 

  Ε_επαγ  =  i  (R₁ + R₂)  =>  B₂ l v =   i  (R₁ + R₂)  =>  i  = B l v / (R₁ + R₂)           

η ράβδος δέχεται δύναμη Laplace  αντίρροπη του βάρους της    m g  -  B₂ l i  =  m a  =>  m g  -  B₂² l² v / (R₁ + R₂) =  m a      το μέτρο της ταχύτητας αυξάνεται  οπότε το μέτρο της επιτάχυνσης μειώνεται  έως ότου μηδενισθεί   τότε  m g  =  B₂² l² v_ορ / (R₁ + R₂)  =>   v_ορ  =  m g(R₁ + R₂) / B₂² l²  =>  v_ορ  =  0,125  10 (4 + 4) / 1² 1²  =>  υ_ορ = 10 m/s      

P_R2 = i² R₂  =>  4 W  =  i²  4  =>  i = 1 A   

  B₂ l v =   i  (R₁ + R₂)  =>  1  1  v =   1  (4 + 4)  =>  v = 8 m/s    ταχύτητα ράβδου

  m g  -  B₂ l i  =  m a  =>  0,125  10  -  1  1  1  =   0,125  a  =>   a  =  0,25 / 0,125  = 2 m/s²  =  dv/dt     επιτάχυνση ράβδου  

 B₂ l v =  i (R₁ + R₂)  =>  B₂ l  dv/dt  =  di/dt  (R₁ + R₂)  =>  1  1  2  =  di/dt  (4 + 4)  =>  di/dt  = 2 / 8 = 0,25 A/s