i = 0,5 W / 0,5 V = 1 A    R_λ = 0,5 V / 1 A = 0,5 Ω      η πλευρα ΔΕ εισέρχεται στο μαγνητιικό πεδίο  αυξάνεται η μαγνητική ροή που διέρχεται από το πλαίσιο   οπότε  αναπτύσσεται  Ε_επαγ = - ΔΦ/Δt = i 2R_λ =>  - d  dy/dt  2 = i 2R_λ =>  - 0,2  v  2 = i 1  =>  i  =  - 0,4 v      η φορά του επαγωγικού ρεύματος είναι αντίθετη της φοράς κινησεως των δεικτών του ρολογιού

  F  -  F_L  =  m a 

     v = g t = 10 t       i = - 4 t 

 H = 0,5 g t²  =  0,5  10  0,5²  =  10/8 =  5/4 =  1,25 m  

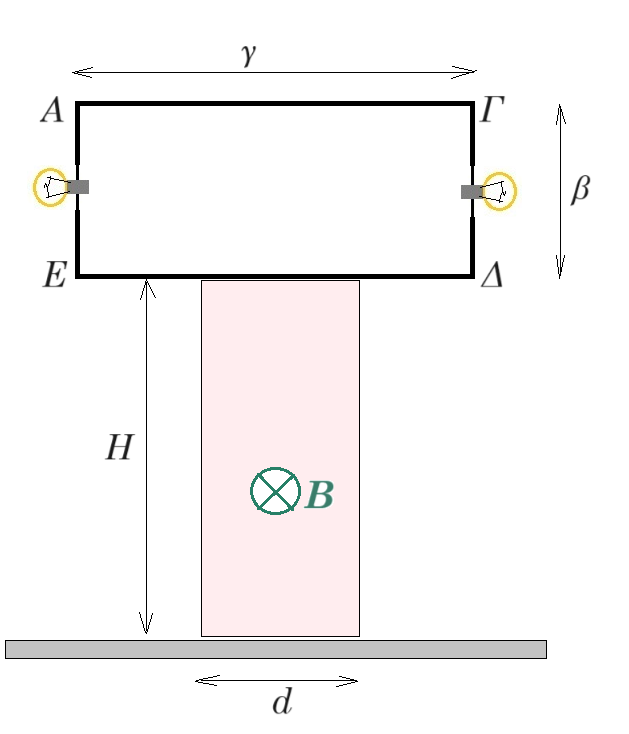
Ορθογώνιο αγώγιμο πλαίσιο ΑΓΔΕ μάζας Μ και αμελητέας αντίστασης έχει συνδεδεμένους στα μέσα των δύο κατακόρυφων πλευρών του ΓΔ και ΕΑ 2 όμοιους λαμπτήρες με στοιχεία κανονικής λειτουργίας P_κ = 0,5 W και V_κ = 0,5 V. Η κάτω πλευρά του πλαισίου εφάπτεται με το άνω όριο οριζόντιου ομογενούς μαγνητικού πεδίου μέτρου Β = 2 Τ και φοράς από τον αναγνώστη προς την σελίδα που η κατακόρυφη τομή του είναι σχήματος παραλληλόγραμμου με οριζόντιες πλευρές μήκους d = 0,2 m και κατακόρυφες πλευρές μήκους Η. Το μαγνητικό πεδίο εκτείνεται μέχρι το έδαφος. Αρχικά το πλαίσιο ισορροπεί ακίνητο. Την χρονική στιγμή t₀ = 0 ασκώντας κατάλληλη δύναμη F στο πλαίσιο αυτό ξενικά κατακόρυφη ομαλά επιταχυνόμενη κίνηση με φορά προς τα κάτω και επιτάχυνση μέτρου α = g. Κατά την διάρκεια της κίνησης του πλαισίου η μέγιστη φωτοβολία των λαμπτήρων επιτυγχάνεται όταν λειτουργούν κανονικά. Την χρονική στιγμή t = 0,5 s έρχεται σε επαφή η πλευρά ΔΕ του πλαισίου με το έδαφος. Δίνονται (ΑΓ) = (ΔΕ) = γ > d,   (ΓΔ) = (ΕΑ) = β < Η και g = 10 m/s². Οι αντιστάσεις του αέρα να θεωρηθούν αμελητέες.
Να υπολογίσετε :
1) την τιμή του Η και την τιμή του β.
2) το φορτίο που διέρχεται από μια διατομή του πλαισίου από 0 έως 0,5 s.
3) την συνάρτηση του μέτρου της εξωτερικής δύναμης με τον χρόνο από 0 έως 0,5 s.
4) την ισχύ της δύναμης Laplace την χρονική στιγμή t = 0,125 s.