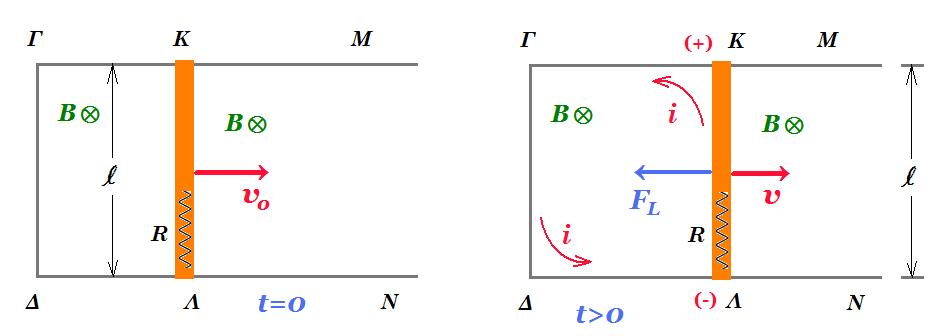
 i = B l v / R
i = B l v / R
ΣF = - b v - D x = m dv/dt => m x" + b x' + D x = 0 => m ρ2 + b ρ + D = 0
Δ = b2 - 4mD = b2 - 4 m m ω02 = - 4m2 ( ω02 - (b/2m)2 ) = - 4m2 ω2 ω02 - Λ2 = ω2
ρ1,2 = ( - β ± Δ½ ) / 2α = ( - b ± j2mω ) / 2m = - b/2m ± jω = - Λ ± jω Λ = b/2m
x(t) = B1 eρ1t + B2 eρ2t = B1 e (- Λ + jω)t + B2 e (- Λ - jω)t = e-Λt ( B1 ημωt + B2 συνωt )
μια λύση είναι : x(t) = A0 e-Λt συνωt
v = dx/dt = - Λ A0 e-Λt συνωt - ω A0 e-Λt ημωt = - A0 e-Λt ( Λ συνωt + ω ημωt )
a = dv/dt = Λ2 A0 e-Λt συνωt + ω Λ A0 e-Λt ημωt + ω Λ A0 e-Λt ημωt - ω2 A0 e-Λt συνωt =>
=> a(t) = A0 e-Λt { ( Λ2 - ω2 ) συνωt + 2ω Λ ημωt }
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
2mg - T = 2ma T - Bil = ma Bvl = iR => i = Blv/R
2mg - Bil = 3ma => 2mg - B2 l2 v/R = 3m dv/dt (1)
παρατηρούμε ότι το μέτρο της επιτάχυνση μειώνεται με τον χρόνο ενώ η ταχύτητα της ράβδου αυξάνεται μετά από πολύ χρόνο η επιτάχυνση μηδενίζεται και η ταχύτητα αποκτά οριακή τιμή η (1) => 2mg - B2 l2 vορ /R = 0 => υορ = 2mRg/B2l2
για υ = υορ/2 = mRg/B2l2 η (1) => 2mg - B2l2/R mRg/B2l2 = 3m α1 =>
=> 2mg - mg = 3m α1 => α1 = g/3
αρχικά υ = 0 i = 0 οπότε η 2mg - Bil = 3m a0 => 2mg - 0 = 3m a0 => α0 = 2g/3
οπότε α0 / α1 = 2
(1) => 2g - B2l2 v/mR = 3 dv/dt =>
=> - B2l2/mR ( v - 2mRg / B2l2 ) = 3 dv/dt =>
=> dv / ( v - 2mRg / B2l2 ) = - B2l2/3mR dt =>
=> ln [ ( v - 2mRg / B2l2 ) / ( - 2mRg / B2l2 ) ] = - B2l2/3mR dt =>
=> v(t) = 2mRg/B2l2 ( 1 - e-B2l2/3mR dt ) a(t) = 2g/3 e-B2l2/3mR dt
t=0 v=0 a0 = 2g/3 t®¥ a=0 vορ = 2mRg/B2l2 v1 = vορ/2 = mRg/B2l2
2mg - B2l2 v1 /R = 3m a1 => 2mg - B2l2/R mRg/B2l2 = 3m a1 =>
=> 2mg - mg = 3m a1 => mg = 3m a1 => a1 = g/3 α0 / α1 = 2
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
μαθηματική ανάλυση :
E - L di/dt = i ( r + R ) => - L di/dt = i ( r + R ) - E =>
=> - L di/dt = ( r + R ) [ i - E/( r + R ) ] => di / [ i - E/( r + R ) ] = - ( r + R )/L dt =>
=> ln { [ i - E/( r + R ) ] / [ I0 - E/( r + R ) ] } = - ( r + R )/L . t =>
=> i(t) = E/( r + R ) + [ I0 - E/( r + R ) ] e- ( r + R )/L . t => i(t) = 24/11 + ( 2 - 24/11 ) . e- 110 . t
=> i(t) = 24/11 - 2/11 . e- 110 . t
i(0) = 24/11 - 2/11 . e0 = 2 A t ® ¥ i ® 24/11 Α
di/dt = [ I0 - E/( r + R ) ] [ - ( r + R ) / L ] . e- ( r + R )/L . t => di/dt = [ E - I0 ( r + R ) ] / L . e- ( r + R )/L . t
di/dt = [ 24 - 2 . 11 ] / 0,1 . e- 110 . t => di/dt = 20 . e- 110 . t
t = 0 di/dt = 20 A/s t ® ¥ di/dt ® 0
U = ½ L i2
dU/dt = L i didt = 0,1 ( 24/11 - 2/11 . e- 110 . t ) 20 . e- 110 . t
t = 0 dU/dt = 0,1 2 20 = 4 J/s t ® ¥ dU/dt ® 0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
 i = B l v / R
i = B l v / R
- FL = m a => - B i l = m a => a = - B i l / m => a = - B2 l2 v / mR = dv/dt =>
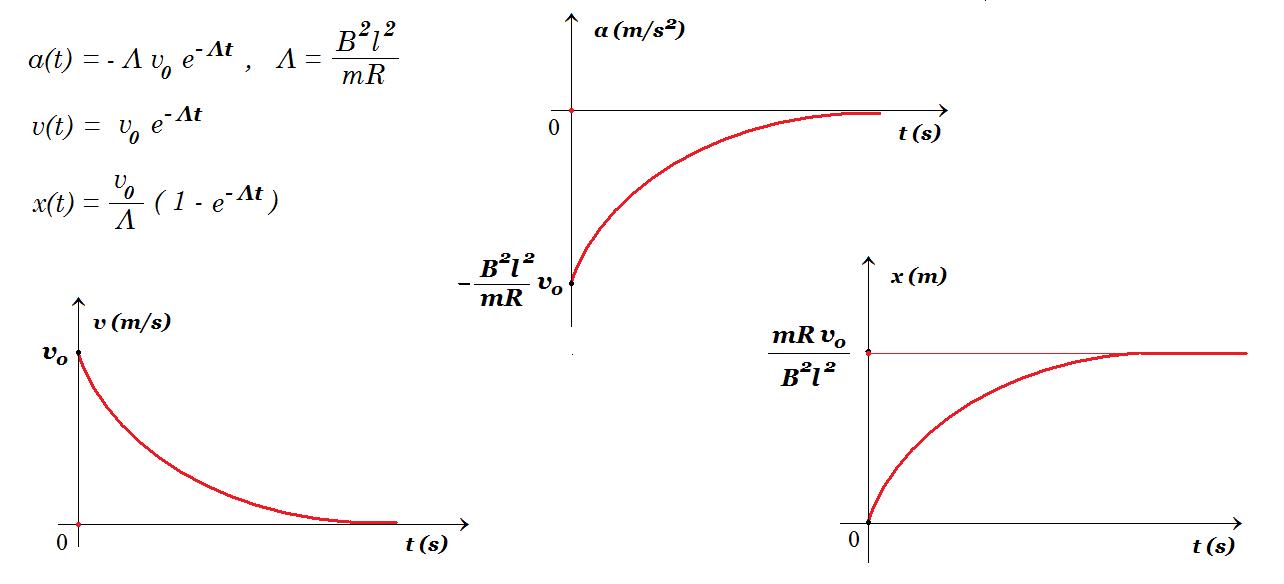
=> dv / v = (- B2 l2 / mR ) dt => ln(v/v0) = (- B2l2/ mR ) t => v(t) = v0 e-Λt , Λ = B2l2/ mR
επιτάχυνση αγωγού : a(t) = - Λ v0 e-Λt , Λ = B2l2/ mR
dx/dt = v0 e-Λt => dx = v0 e-Λt dt = - v0/Λ d(e-Λt) => x(t) - x(0) = - (v0/Λ) (e-Λt - 1) =>
=> x(t) = (v0/Λ) ( 1 - e-Λt ) , Λ = B2l2/ mR
x(0) = 0 x(¥) = v0 mR / B2l2
..................................................................................................................................................................
Εεπαγ = Β υ l = i ( R1 + R2 ) => 2 T v 0,5 m = i ( 2 Ω + 8 Ω ) => 10 i = v => i = 0,1 v
PR2 = I2 R2 => 8 Watt = I2 8 Ω => I = 1 A αρχική τιμή ρεύματος
άρα 10 i = v => 10 Ι = v0 => v0 = 10 m/s αρχική ταχύτητα αγωγού
ΣF = m a => F - FL = m a => F - B i l = m a => 0,5 - 2 0,1 v 0,5 = 0,1 a => a = 5 - v αρχικά την χρονική στιγμή t = 0 v = v0 a = a0 = 5 - v0 = 5 - 10 = - 5 m/s2
όταν α = 0 τότε v = 5 m/s = vορ οριακή ταχύτητα αγωγού
a = 5 - v = dv/dt => dv / (5 - v) = dt => dv / (v - 5) = - dt => ln [ (v - 5 )/( 10 - 5) ] = - t =>
=> v - 5 = 5 e-t => v(t) = 5 + 5 e-t v(0) = 5 + 5 = 10 m/s
a = dv/dt => a(t) = - 5 e-t a(0) = - 5 m/s2
Εεπαγ = Β υ l = 2T 0,5m ( 5 + 5 e-t ) = 5 + 5 e-t = Εεπαγ(t)
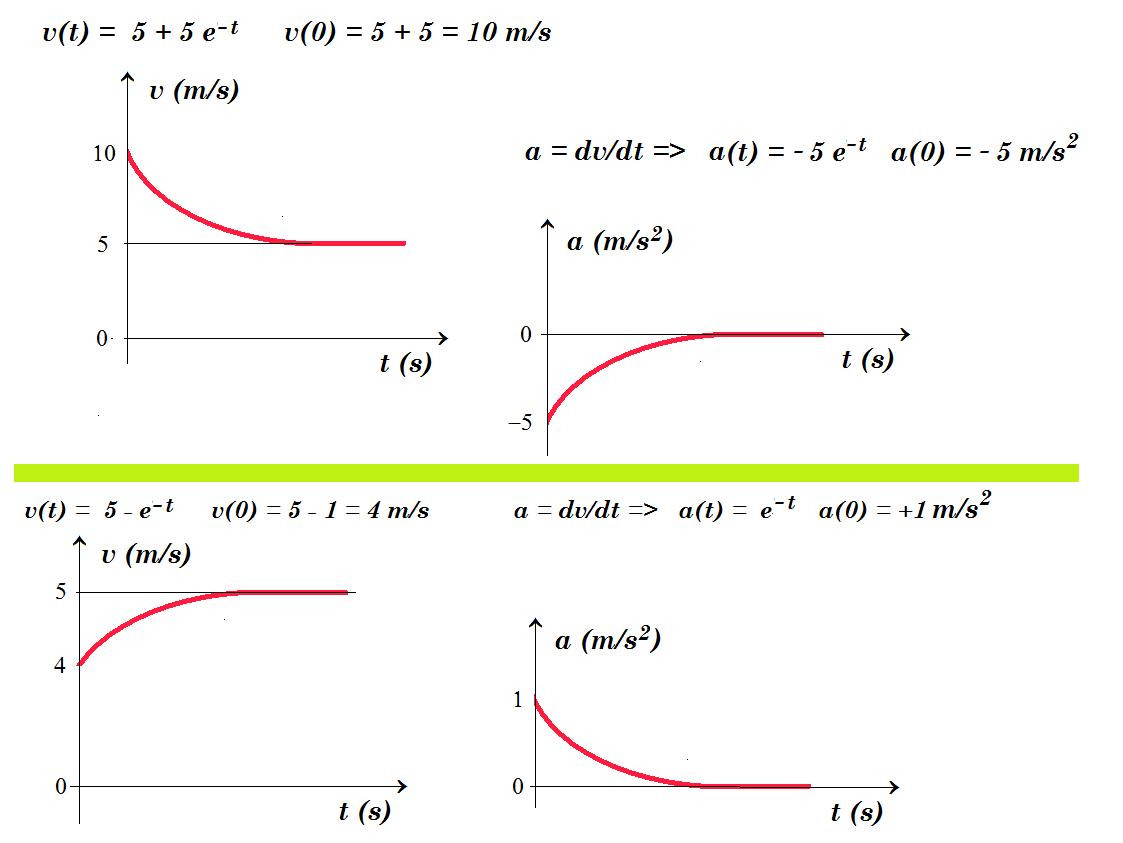
a = 5 - v αρχικά την χρονική στιγμή t = 0 v = v0 = 4 m/s a = a0 = 5 - v0 = 5 - 4 = +1 m/s2
a = 5 - v = dv/dt => dv / (5 - v) = dt => dv / (v - 5) = - dt => ln [ (v - 5 )/( 4 - 5) ] = - t =>
=> v - 5 = -1 e-t => v(t) = 5 - e-t v(0) = 5 - 1 = 4 m/s a = dv/dt => a(t) = e-t a(0) = +1 m/s2