ΘΈΜΑ Δ.
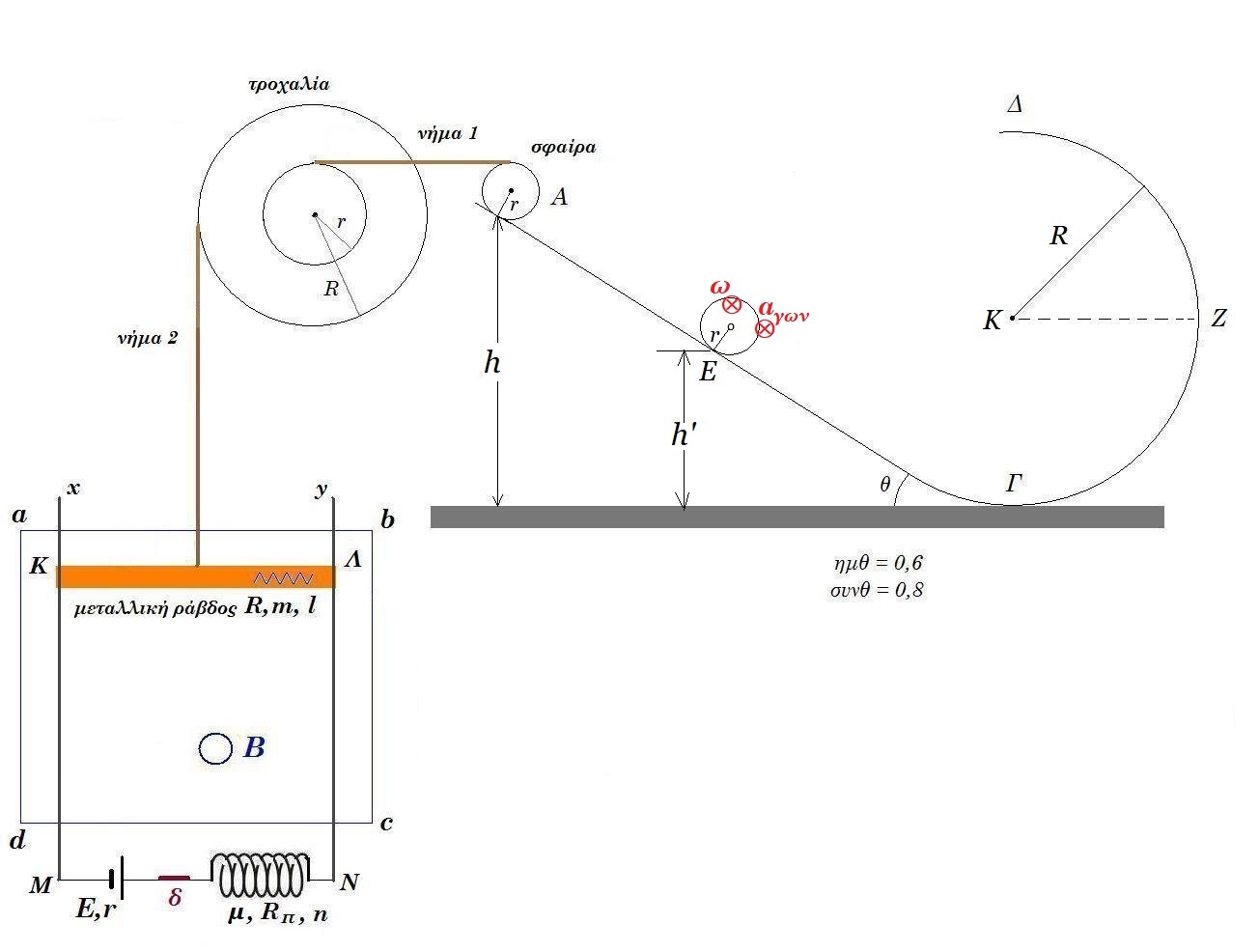
Θεωρούμε την διάταξη του σχήματος, σε κατάσταση ισορροπίας, σε κατακόρυφο επίπεδο. Στη θέση Α του κεκλιμένου επιπέδου ισορροπεί ομογενής σφαίρα μάζας m = 3kg , ακτίνας r = 0,1m. Το κεκλιμένο επίπεδο γωνίας κλίσεως θ, ( ημθ = 0,6 συνθ = 0,8 ) στην βάση του συνδέεται με κατακόρυφο ημικύκλιο ακτίνας R = 1m. Η σφαίρα στο άνω της άκρο συνδέεται με οριζόντιο αβαρές μη εκτατό νήμα 1 (σταθερού μήκους) με τροχαλία μάζας Μ = 5kg εσωτερικής ακτίνας rτροχ = 0,2m , εξωτερικής ακτίνας Rτροχ = 0,5m. Η τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από άξονα που διέρχεται από το κέντρο της και είναι κάθετος στο επίπεδο της. Γύρω από την τροχαλία έχουμε τυλίξει αρκετές φορές αβαρές μη εκτατό νήμα 2 το οποίο συνδέεται με την μεταλλική ράβδο ΚΛ στο μέσον αυτής. Η μεταλλική ράβδος ισορροπεί σε οριζόντια θέση, έχει μήκος l = 1m και μάζα m=0,5kg, είναι σε επαφή με κατακόρυφους αγωγούς Mx, Ny. Το πηνίο φέρει 1000 σπείρες/m, διαρρέεται από συνεχές ρεύμα εντάσεως Ι, ενώ στο κέντρο του το μέτρο της εντάσεως του μαγνητικού πεδίου είναι Βπην = 4π 10-3 Tesla. Στον χώρο abcd υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο εντάσεως Β.
Δ1. Βρείτε την ένταση του μαγνητικού πεδίου Β φορά, μέτρο. μονάδες 8
Κάποια στιγμή ( t = 0 ) αφαιρούμε το νήμα 1 και ταυτόχρονα ανοίγουμε τον διακόπτη δ, οπότε η σφαίρα κατέρχεται επί του κεκλιμένου επιπέδου κυλιόμενη ( μη ολισθαίνουσα ) ενώ η ράβδος κινείται κατακόρυφα προς τα κάτω ενώ είναι συνεχώς σε επαφή με τους αγωγούς Mx, Ny και η τροχαλία περιστρέφεται γύρω από τον άξονά της χωρίς τριβές έχοντας γωνιακή επιτάχυνση αγων = 10/3 rad/s2 .
Δ2. Εξηγείστε γιατί φορτίζεται η κατερχόμενη ράβδος ΚΛ. Εκφράστε την τάση VΛΚ στα άκρα της, συναρτήσει του χρόνου εάν η ένταση του μαγνητικού πεδίου έχει μέτρο Β = 0,1 Τesla. μονάδες 5
Η σφαιρα κυλίεται ( δεν ολισθαίνει ) κινούμενη στο κεκλιμένο επίπεδο, διέρχεται από την θέση Γ, ανέρχεται κυλιόμενη στο ημικύκλιο και διέρχεται από την ανώτατη Δ του ημικυκλίου έχοντας ταχύτητα μέτρου υ = 3m/s.
Δ3. Η σφαίρα κυλιόμενη επί του κεκλιμένου επιπέδου έχει γωνιακή επιτάχυνση αγων = 300/7 rad/s2. Βρείτε την ταχύτητα του ανώτερου σημείου της σφαίρας τη χρονική στιγμή t = 1s που βρίσκεται στο σημείο Ε σε ύψος h'. μονάδες 7
Δ4. Όταν η σφαίρα διέρχεται από την θέση Δ βρείτε την δύναμη που δέχεται από το ημικύκλιο καθώς και την γωνιακή ταχύτητάς της ( διεύθυνση, φορά, μέτρο ) μετά από 0,2 sec. μονάδες 5
Δίνονται : μαγνητική διαπερατότητα του κενού μο = 4π 10-7 Ν/Α2 , επιτάχυνση βαρύτητας g = 10 m/s2

.............................................................................................................................................................
ΘΕΜΑ Δ
ισορροπία σφαίρας
ροπές ως προς το κέντρο της σφαίρας : Στ = 0 => Τ2 r = Ττρ r => Τ2 = Ττρ
οριζόντιος άξονας : Τ2 + Ττρ συνθ = Ν ημθ => Τ2 + Τ2 0,8 = Ν 0,6 => 1,8 Τ2 = 0,6 Ν => Ν = 3 Τ2
κατακόρυφος άξονας : Ττρ ημθ + Ν συνθ = mg => Τ2 0,6 + 3 Τ2 0,8 = 30 => 3Τ2 = 30 => Τ2 = 10Ν
ισορροπία τροχαλίας : ροπές ως προς το κέντρο : Στ = 0 => Τ2 rτροχ. = Τ1 Rτροχ. =>
=> 10 N 0,2 m. = Τ1 0,5 m => T1 = 4 N
ισορροπία ράβδου : ΣFy = 0 => T1 + FL = mg => 4N + FL = 0,5 10 => FL = 1 Newton κατακόρυφη με φορά προς τα πάνω
Βπην = 4π 10-7 i n => 4π 10-3 = 4π 10-7 i 1000 => i = 10 A
FL = B i l => 1Ν = B 10Α 1m => B = 0,1 Tesla με φορά προς τα έξω
Δ2. η ράβδος κατέρχεται με επιτάχυνση α = αγων R = 10/3 rad/s2 0,5 m = 5/3 m/s2
τότε v = a t = 5/3 t
Εεπαγ = Β l v = 0,1 T 1 m 5/3 t = t/6 = VΚΛ Κ (+) Λ(-) VΛΚ = - t/6
Δ3. αγων = 300/7 rad/s2 ω = αγων t = 300/7 rad/s2 1 s = 300/7 rad/s
acm = αγων r = 300/7 rad/s2 0,1 m => acm = 30/7 m/s2
υcm = ω r = 300/7 0,1 = 30/7 m/s
υ2 = υcm2 + (ω r)2 + 2 υcm ω r συνθ = 2 υcm2 ( 1 + συνθ ) = 2 (30/7)2 (1 + 0,8 ) =
= 3,6 (30/7)2 => υ = 3,6½ 30/7 m/s
Δ4. όταν η σφαίρα διέρχεται από την ανώτερη θέση Δ με υΔ = 3 m/s :
ΣFy = Fκ => mg + Ν = m vΔ2 / (R - r) => 30Ν + Ν = 3kg (3m/s)2 / (1m - 0,1m) =>
=> Ν = 30N - 3 9 / 0,9 = 0
άρα μόλις η σφαίρα διέρχεται από την ανώτερη θέση Δ του ημικυκλίου Ν = 0
η σφαίρα στον αέρα δεν δέχεται δύναμη που να δημιουργεί ροπή συνεπώς η γωνιακή ταχύτητά της είναι σταθερή : ω = υΔ / r = 3 m/s / 0,1 m = 30 rad/s
