ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ

ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΨΥΧΙΚΟΥ

ΤΑΞΗ :  Γ' ΛΥΚΕΙΟΥ
ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ :   ΦΥΣΙΚΗ

ΗΜΕΡΟΜΗΝΙΑ :   19 / 4 / 2024                  Ονοματεπώνυμο : 

                                                                  ΘΈΜΑΤΑ

ΘΈΜΑ Α.

Α1.  
α)  στο κέντρο Ο του κυκλικού βρόχου η ένταση του μαγνητικού πεδίου έχει μέτρο ανάλογο της γωνίας φ  και για το ευθύγραμμο σύρμα, στο εσωτερικό του το πεδίο είναι αντιστρόφως ανάλογο της απόστασης r.   
β)  στο κέντρο Ο του κυκλικού βρόχου η ένταση του μαγνητικού πεδίου είναι κάθετη στο επίπεδο της σελίδας με φορά προς την σελίδα και για το ευθύγραμμο σύρμα, στο εξωτερικό του το πεδίο είναι ανάλογο της απόστασης r. 
γ)  στο εσωτερικό του ευθυγράμμου σύρματος  η ένταση του μαγνητικού πεδίου έχει μέτρο αντιστρόφως ανάλογο της απόστασης r  και  στο εξωτερικό του το πεδίο είναι  ανάλογο της απόστασης r.   
δ)  στο κέντρο Ο του κυκλικού βρόχου η ένταση του μαγνητικού πεδίου έχει μέτρο ανάλογο της γωνίας φ, για το ευθύγραμμο σύρμα στο εσωτερικό του το πεδίο είναι ανάλογο της απόστασης r.              
                                                                                                                 μονάδες 5
 
 
 

Α2.     Σώμα εκτελεί ΑΑΤ,  στο σχήμα φαίνεται το διάγραμμα υ(t) της ταχύτητας συναρτήσει του χρόνου.

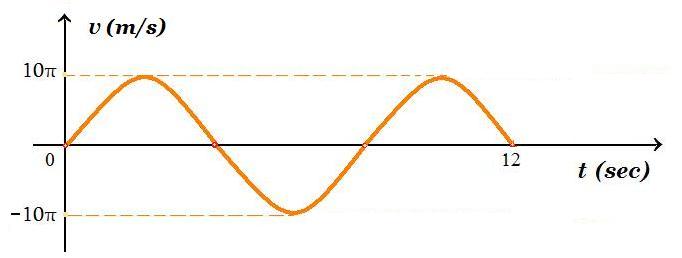Η εξίσωση της απομάκρυνσης  συναρτήσει του χρόνου είναι :
  (α)  x(t) = 10 ημ(π/4 t + π/2)             (β)  x(t) = 40 ημ(π/4 t + π/2)  
  (γ)  x(t) = 40 ημ(π/4 t + 3π/2)           (δ)  x(t) = 30 ημ(π/3 t + π/2)               
                                                                                                                 μονάδες 5
 
Α3. 
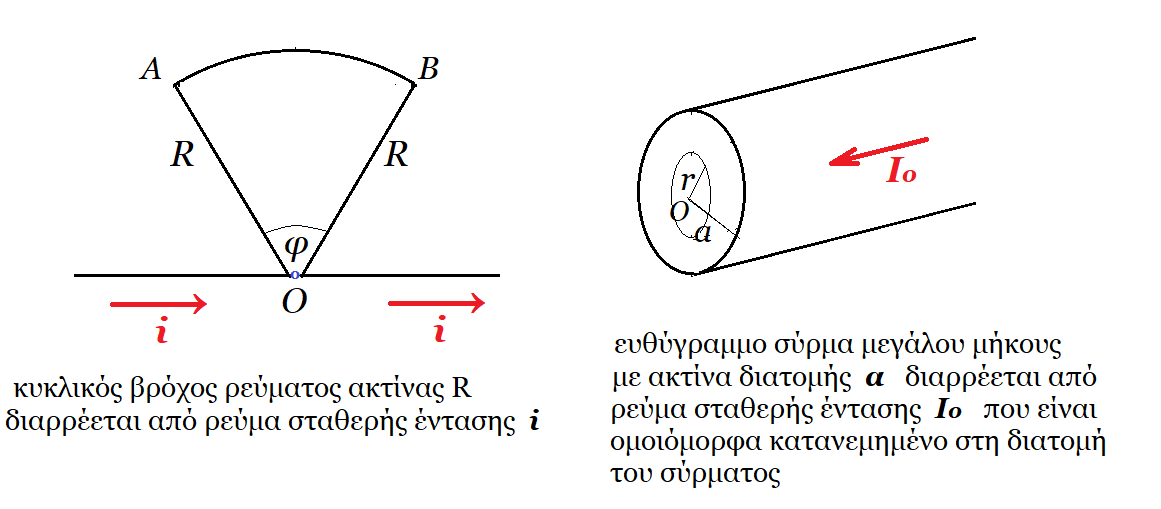
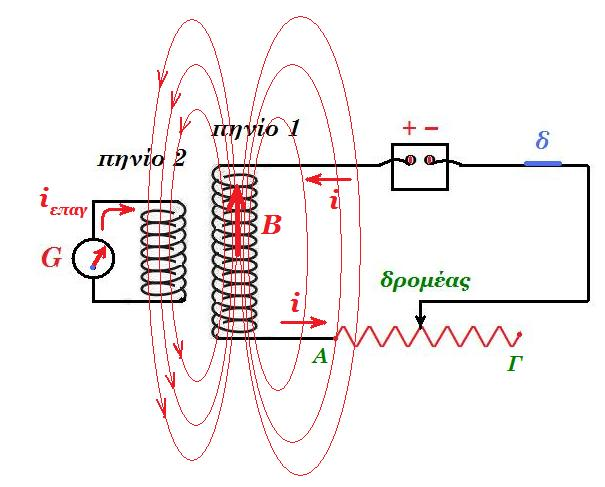
Στο κύκλωμα του σχήματος  μια ηλεκτρική πηγή συνεχούς ρεύματος συνδέεται με μεταβλητή αντίσταση (ροοστάτης)  και δύο κλάδους παράλληλους.  Ο ένας κλάδος περιλαμβάνει λαμπτήρα με ωμική αντίσταση RΛ και ο άλλος πηνίο με ωμική αντίσταση Rπ  ( RΛ > Rπ ).  Ο διακόπτης  δ  είναι κλειστός. 

α)    Μετακινούμε τον δρομέα από το άκρο Α  του ροοστάτη προς το άκρο Γ  σε χρονικό διάστημα Δt.  

    i)    το πηνίο  "αντιδρά"  και το άκρο του  Λ  γίνεται βόρειος πόλος   

    ii)   ο λαμπτήρας φωτοβολεί εντονότερα για χρονικό διάστημα Δt

    iii)  το πηνίο διαρρέεται από ρεύμα μεγαλύτερης έντασης

    iv)  τίποτα από τα ανωτέρω.

β)    Τοποθετούμε τον δρομέα σε ορισμένη θέση έτσι ώστε ο λαμπτήρας να φωτοβολεί ελάχιστα και  ανοίγουμε τον διακόπτη.  

    i)    ο λαμπτήρας σβήνει αμέσως

    ii)   ο λαμπτήρας φωτοβολεί αμυδρά για μικρό χρονικό διάστημα και μετά σβήνει

    iii)  ο λαμπτήρας αρχικά φωτοβολεί πιο έντονα  και μετά σβήνει

    iv)  τίποτα από τα ανωτέρω.

                                                                                                                 μονάδες  2 + 3

 
Α4.   
Οι διπλοί αστέρες, είναι αστέρες  οι οποίοι λόγω της βαρύτητάς τους, περιστρέφονται γύρω από ένα κοινό κέντρο μάζας.  Ο μεγαλύτερος αστέρας ονομάζεται πρωτεύοντας ή κύριος ενώ ο άλλος, συνήθως μικρότερος, ονομάζεται συνοδός ή δευτερεύων αστέρας.  Έστω ο αστέρας Α  έχει μάζα Μ1  ενώ ο αστέρας Β έχει μάζα Μ2 = ½ Μ1  και περιστρέφονται γύρω από το κοινό κέντρο μάζας τους Ο.  Τα κέντρα μάζας τους απέχουν από το Ο αποστάσεις r1 , r2  αντίστοιχα.  Θεωρούμε ότι περιστρέφονται με σταθερή συχνότητα f  γύρω από το Ο  και  τα μέτρα των στροφορμών τους είναι αντίστοιχα  L1 , L2.  Κάθε σώμα ανάλογα την θερμοκρασία που έχει εκπέμπει "θερμική ακτινοβολία".  Ένας αστέρας φαίνεται ερυθρός διότι εκπέμπει στο ερυθρό του ορατού φάσματος της ακτινοβολίας. Ένας αστέρας φαίνεται κυανούς διότι εκπέμπει στο κυανού του ορατού φάσματος της ακτινοβολίας. Έστω ότι ο αστέρας Α φαίνεται ερυθρός  και  ο αστέρας Β  φαίνεται κυανούς.
(α)  Ο αστέρας Α έχει υψηλότερη θερμοκρασία στην επιφάνειά του απ' ότι ο αστέρας Β και ισχύει L1 = L2. 
(β)  Ο αστέρας Β έχει την ίδια θερμοκρασία στην επιφάνειά του όπως ο αστέρας Α και ισχύει  2 L1 = L2.
(γ)  Ο αστέρας Α έχει υψηλότερη θερμοκρασία στην επιφάνειά του απ' ότι ο αστέρας Β και ισχύει  L1 = 2 L2.
(δ)  Ο αστέρας Β έχει υψηλότερη θερμοκρασία στην επιφάνειά του απ' ότι ο αστέρας Α και ισχύει  2 L1 = L2.
Η ελκτική δύναμη μεταξύ ουρανίων (σφαιρικών) σωμάτων με μάζες Μ1 και Μ2 δίνεται από τη σχέση :  FG = G M1 M2 / d2  όπου  d  είναι η απόσταση μεταξύ των κέντρων των σωμάτων.
                                                                                                                 μονάδες 5
 

Α5.   Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα την λέξη Σωστό, για την σωστή πρόταση, και την λέξη Λάθος, για την λανθασμένη.

α.  Μεταλλική σφαίρα αμελητέας ακτίνας φέρει ηλεκτρικό φορτίο  - 17∙10-19 C.

β.  Ο νόμος του Ampere ισχύει όταν τα ηλεκτρικά ρεύματα είναι εναλλασσόμενα.
γ.  Σε χαμηλές θερμοκρασίες το μέλαν σώμα εκπέμπει στο υπέρυθρο.

δ.  Ένα ηλεκτρόνιο περιστρέφεται γύρω από συνεχώς ακίνητο πρωτόνιο με σταθερή συχνότητα περιστροφής f  σε ακτίνα r.  Το διάνυσμα της στροφορμής  L  του ηλεκτρονίου  και  το διάνυσμα της έντασης Β του μαγνητικού πεδίου   που δημιουργεί, είναι ομόρροπα.

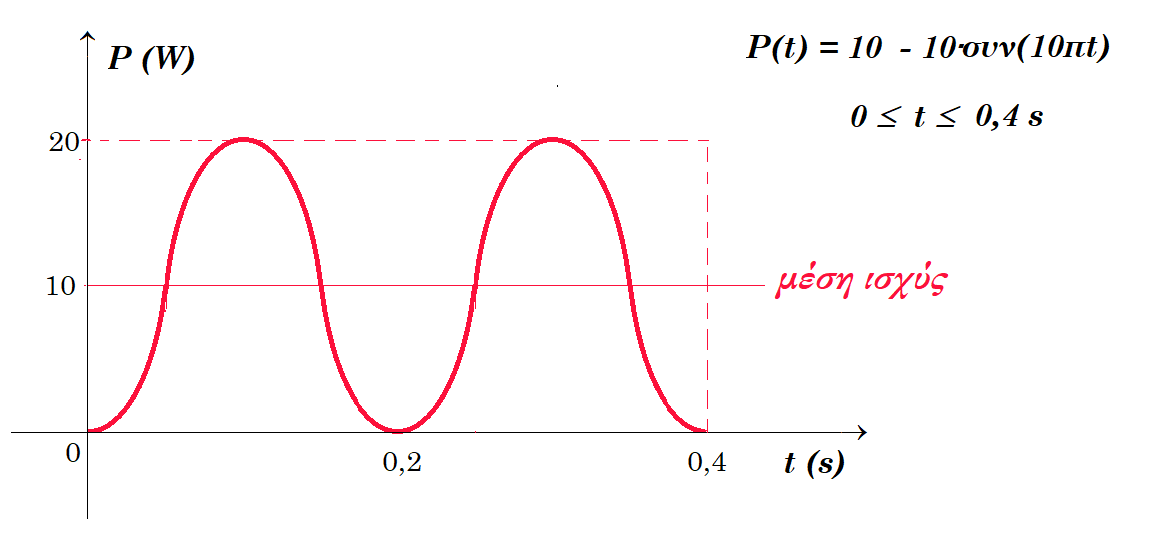
ε.  Στα άκρα αντίστασης 10 Ω εφαρμόζεται εναλλασσόμενη τάση.  Η ισχύς που καταναλώνεται στην αντίσταση φαίνεται στο διάγραμμα P(t).  H ένταση του ρεύματος συναρτήσει του χρόνου είναι :  i(t) = 2∙ημ(5πt).

                                                                                                                 μονάδες 5

 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘΈΜΑ Β.

 Β1.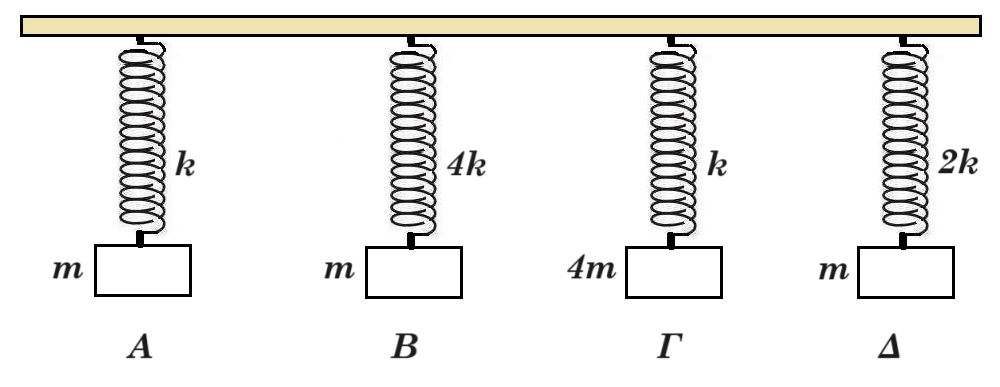

 Σε ομογενή σανίδα συνδέονται οι ταλαντωτές του σχήματος.  Διεγείρουμε την σανίδα ωστε να κάνει Α.Α.Τ. με συχνότητα  f1  Παρατηρούμε ότι τα σώματα  Α  και Γ ταλαντώνονται με το ίδιο πλάτος.

Α)  Η συχνότητα  f1  ισούται με :         α)  1/π √(k/m)        β)  1/2π √(k/m)      γ)  1/2π √(2k/m)                  

Επιλέξτε την σωστή απάντηση.          μονάδες  1               
Δικαιολογήστε την επιλογή σας.        μονάδες  5           
Β)  Ο ταλαντωτής Β  ταλαντώνεται με :   μεγαλύτερο,    μικρότερο,  ίσο    πλάτος με τον ταλαντωτή Α. 
Επιλέξτε την σωστή απάντηση.          μονάδες  1               
Δικαιολογήστε την επιλογή σας.        μονάδες  4 
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
 

Β2.   Στο σχήμα ο δρομέας της μεταβλητής αντίστασης μετακινείται από το άκρο Α στο άκρο Γ. Το πηνίο 2 διαρρέεται από επαγωγικό ρεύμα όπως έχει σημειωθεί στο σχήμα.  Σωστό  ή  Λάθος   Δικαιολογήστε την επιλογή σας.  μονάδες  1 + 6

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

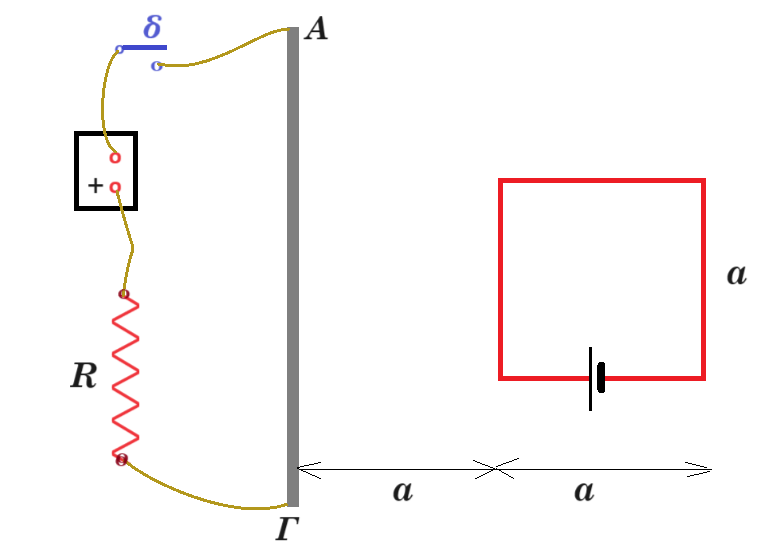
Β3.   Στο σχήμα η διάταξη είναι επάνω σε λείο οριζόντιο επίπεδο,  το συρμάτινο πλαίσιο πλευράς  α  διαρρέεται από ρεύμα Ι2  ενώ ο διακόπτης  δ  στο κύκλωμα είναι ανοικτός.  Τη στιγμή t0 = 0  κλείνουμε τον διακόπτη οπότε ο ευθύγραμμος αγωγός ΑΓ  διαρρέεται από ρεύμα  Ι1.  Το συρμάτινο πλαίσιο αποκτά επιτάχυνση :

    α)  οριζόντια δεξιά με μέτρο  10-7 2 Ι1 Ι2 / m                      β)  οριζόντια αριστερά με μέτρο  10-7 Ι1 Ι2 / m   

    γ)  οριζόντια αριστερά με μέτρο  10-7 2 Ι1 Ι2 / m               δ)  οριζόντια δεξιά με μέτρο  10-7  Ι1 Ι2 / 2m     

Επιλέξτε την σωστή απάντηση.          μονάδες  1               
Δικαιολογήστε την επιλογή σας.        μονάδες  6      

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘΈΜΑ Γ.

Η διπλή τροχαλία του σχήματος με ακτίνες  r1 = 0,05 m και r2 = 2r1, μπορεί να στρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα περιστροφής, που διέρχεται από το κέντρο της.   Η τροχαλία έχει αμελητέα μάζα, δηλαδή κάθε στιγμή ισχύει για αυτήν ότι το άθροισμα των ροπών που της ασκούνται ως προς τον άξονα περιστροφής της είναι ίσο με μηδέν,  είτε ισορροπεί, είτε περιστρέφεται.   Γύρω από το εξωτερικό αυλάκι της τροχαλίας υπάρχει τυλιγμένο ένα αβαρές και μη εκτατό νήμα, στο άκρο του οποίου είναι δεμένο ένα σώμα Σ2 μάζας    m2 = 0,5 kg. Στο εσωτερικό αυλάκι της τροχαλίας είναι επίσης τυλιγμένο ένα αβαρές και μη εκτατό νήμα, το άκρο του οποίου είναι δεμένο στο μέσο μιας ομογενούς  μεταλλικής ράβδου, ΚΛ, μήκους  L = 1 m, αντίστασης R3 και μάζας m1 = 0,2 kg,  η οποία μπορεί να κινείται πάνω στους οριζόντιους, αγώγιμους – αμελητέας αντίστασης - οδηγούς Αx και Γx’.   Ο συντελεστής οριακής τριβής μεταξύ των οδηγών και της ράβδου ΚΛ έχει τιμή μs = 0,5 και είναι ίσος με το συντελεστή τριβής ολίσθησης  (μs=μολ). 
Στο χώρο υπάρχει κατακόρυφο ομογενές μαγνητικό πεδίο έντασης μέτρου  Β = 2 T  με τη φορά των δυναμικών γραμμών προς τα κάτω.  Τα σημεία του κυκλώματος Α, Γ  συνδέονται μέσω του μεταγωγού δ, είτε με ηλεκτρική πηγή ΗΕΔ Ε = 9 V  και εσωτερικής αντίστασης R1 = 1 Ω, είτε με αντίσταση R2 = 1 Ω.   Στην αρχή ο μεταγωγός δ βρίσκεται στη θέση Ζ και η ράβδος ισορροπεί με την τριβή να έχει φορά προς τα αριστερά και μέτρο ίσο με το μέτρο της οριακής τριβής.

Γ1.   Να υπολογίσετε την αντίσταση R3 της μεταλλικής ράβδου ΚΛ.      μονάδες 6                      

Την χρονική στιγμή t=0  φέρνουμε τον μεταγωγό δ  στη θέση Ε και η ράβδος αρχίζει να κινείται πάνω στους οδηγούς.          
Γ2.   Μελετήστε την κίνηση ράβδου  και  σώματος Σ2.  Υπολογίστε την τάση στα άκρα του αντιστάτη R2 την χρονική στιγμή που το σώμα Σ2 κατέρχεται με επιτάχυνση α2 = 2 m/s2.         μονάδες 7           

Γ3.   Να υπολογίσετε την μέγιστη ( οριακή ) ταχύτητα υορ που θα αποκτήσει το σώμα Σ2.     μονάδες 6               

Γ4.   Για το χρονικό διάστημα που απαιτείται για να κάνει η τροχαλία 9 στροφές μετά από την χρονική στιγμή που το σώμα Σ2 αποκτά την οριακή ταχύτητα, να υπολογίσετε τη μείωση της δυναμικής ενέργειας του σώματος Σ2 και να επιβεβαιώσετε την ισχύ της διατήρησης της ενέργειας.      Δίνεται g=10 m/s2       μονάδες 6                    

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘΈΜΑ Δ.

H εξίσωση που περιγράφει την ένταση του ηλεκτρικού πεδίου σε ένα ηλεκτρομαγνητικό κύμα το οποίο διαδίδεται στο κενό  ή  στην ατμόσφαιρα της Γης  είναι :   Ε(x,t) = 300.ημ(2π·1018t - 2π·x/λ) (SI).
Δ1.  Να γραφεί η εξίσωση που περιγράφει την ένταση του μαγνητικού πεδίου  και  να εξεταστεί αν το κύμα αυτό ανήκει στην ορατή περιοχή του φάσματος.      μονάδες 4
Δ2.  Να σχεδιαστεί το στιγμιότυπο της έντασης του ηλεκτρικού πεδίου του κύματος τη στιγμή t=2·10-18s.      μονάδες 4

Δ3.  Το  Η/Μ κύμα προσπίπτει κάθετα σε κατακόρυφα τοποθετημένη μεταλλική επιφάνεια  στο σημείο Ο  και ανακλάται χωρίς απώλεια ενέργειας. Το ανακλώμενο κύμα δημιουργεί με το προσπίπτον, στάσιμο κύμα. Στο σημείο Ο δημιουργείται δεσμός. Πόση είναι η απόσταση μεταξύ του 2ου δεσμού  και  της 5ης κοιλίας του στασίμου Η/Μ κύματος.   μονάδες 3

Δ4.  Ένα φωτόνιο της ηλεκτρομαγνητικής ακτινοβολίας συχνότητας f = 1020 Hz σκεδάζεται από ένα ακίνητο ηλεκτρόνιο. Το σκεδαζόμενο φωτόνιο κινείται κάθετα προς τη διεύθυνση του προσπίπτοντος φωτονίου.  Στο χώρο υπάρχει ομογενές μαγνητικό πεδίο εντάσεως Β=0,01Τ.  Να υπολογίσετε την εφαπτομένη της γωνίας που σχηματίζει η ταχύτητα του ηλεκτρονίου αμέσως μετά την σκέδαση, με τη διεύθυνση της κίνησης του αρχικού φωτονίου.   Μελετήστε την κίνηση του σκεδαζόμενου ηλεκτρονίου μέσα στο μαγνητικό πεδίο εάν η ταχύτητά του αμέσως μετά την σκέδαση σχηματίζει με τις δυναμικές γραμμές του πεδίου γωνία 45°.     μονάδες 3+3

Δ5.  Φωτίζουμε την κάθοδο στο φωτοηλεκτρικό φαινόμενο που είναι η επιφάνεια ενός μετάλλου, με "πράσινο φως"  λ = 500 nm,  ενώ υπάρχει διαφορά δυναμικού V = +1 V.  (α)  Υπολογίστε την κινητική ενέργεια ενός ηλεκτρονίου που εξέρχεται από την επιφάνεια του μετάλλου όταν φθάνει στην άνοδο.   Το έργο εξαγωγής του μετάλλου είναι  2,4 eV.   (β)  Πόση είναι η τάση αποκοπής των ηλεκτρονίων της καθόδου;   (γ)  Αν το έργο εξαγωγής του μετάλλου είναι  6,25 eV (λευκόχρυσος) πόση είναι η μέγιστη τάση μεταξύ ανόδου και καθόδου ώστε τα ηλεκτρόνια να φθάσουν με μέγιστη ταχύτητα στην άνοδο;    μονάδες 3+3+2

 h = 6,6 10-34 J.s         h / mc = 2,4 pm       c = 3 108 m/s       1 eV = 1,6 10-19 J       λ' - λ  =  h / mc (1 - συνφ) 

 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~   

 

ΘΕΜΑ Β  

Β1.  Ομογενής τροχαλία μάζας Μ και αμελητέου πάχους αποτελείται από δύο συγκολλημένους δίσκους με ακτίνες r και R, όπου R =2r. Ο μικρότερος δίσκος ακτίνας r φέρει ένα αυλάκι στην περιφέρειά του γύρω από το οποίο είναι τυλιγμένο πολλές φορές λεπτό, αβαρές και μη εκτατό νήμα, στο ελεύθερο άκρο του οποίου είναι δεμένο βαρύδι μάζας m. Η τροχαλία ακουμπά στην επιφάνεια κεκλιμένου επιπέδου γωνίας κλίσης θ, όπου ημθ=1/10.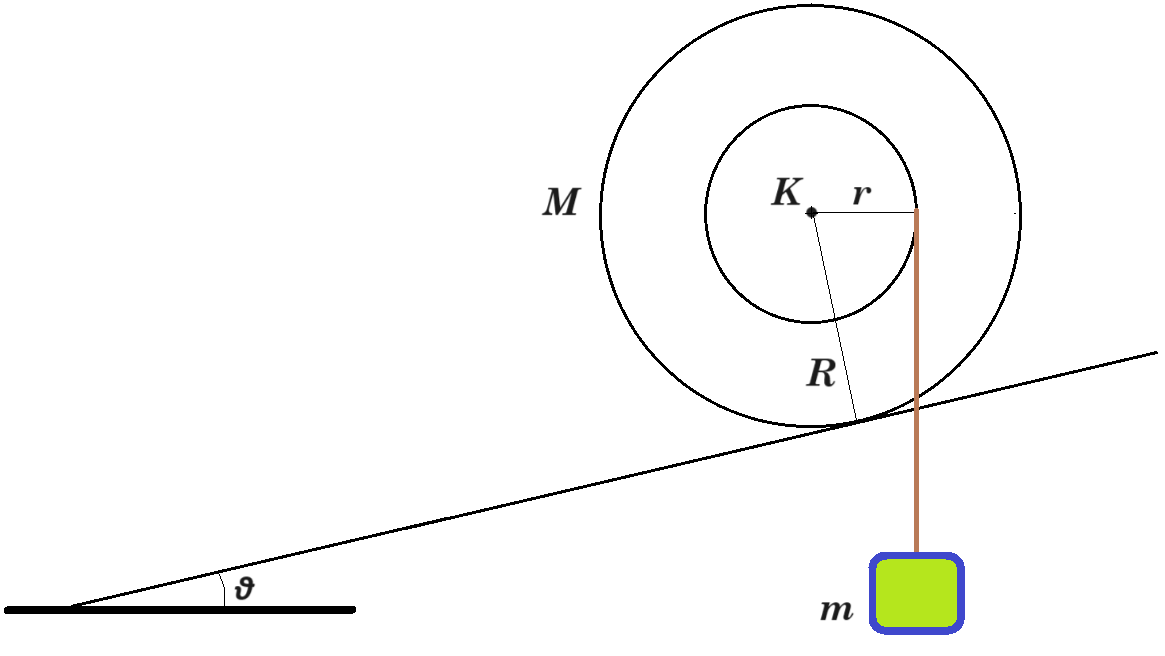 Αν όλη η διάταξη ισορροπεί στατικά και οριακά μέσα σε βαρυτικό πεδίο έντασης μέτρου g, στο οποίο η αντίσταση του αέρα είναι αμελητέα, τότε

1)  ο συντελεστής της μέγιστης στατικής (οριακής) τριβής  μσ  μεταξύ τροχαλίας και επιπέδου είναι ίσος με:

i)  σφθ          ii)  εφθ           iii)  συνθ

2)  ο λόγος των μαζών του βαρυδίου προς της τροχαλίας m/M ισούται με

i)  1/6           ii)  1/4            iii)  1/2

 

ΘΕΜΑ 4

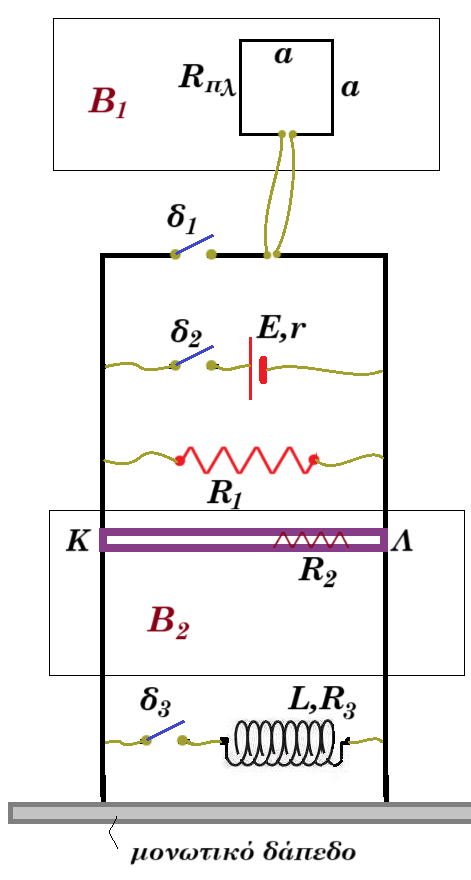Στο σχήμα, το τετράγωνο πλαίσιο πλευράς α = 0,4 m δημιουργήθηκε από σύρμα μήκους lσυρ = 40 m που παρουσιάζει αντίσταση ανά μονάδα μήκους R* = 0,05 Ω/m. Το πλαίσιο βρίσκεται μέσα σε μαγνητικό πεδίο Β1, κάθετα στις δυναμικές γραμμές, με το μέτρο της έντασης του μαγνητικού πεδίου να μεταβάλλεται με τον χρόνο, σύμφωνα με τη σχέση Β1 = 2,5.t (S.I).  Η ηλεκτρική πηγή έχει ΗΕΔ Ε = 8 V και εσωτερική αντίσταση r. Αντιστάτης έχει ωμική αντίσταση R1 = 12 Ω.  Οριζόντια τοποθετημένη ράβδος μήκους (ΚΛ)=1m και αντίστασης R2 = 4 Ω, εφάπτεται διαρκώς στα κατακόρυφα σύρματα (αμελητέας αντίστασης). Η ράβδος βρίσκεται σε ομογενές μαγνητικό πεδίο με Β2 = 2 Τ, κάθετα στις δυναμικές γραμμές. Αρχικά όλοι οι διακόπτες είναι ανοιχτοί. Τη χρονική στιγμή t=0, κλείνουμε τον διακόπτη δ1 και παρατηρούμε ότι η ράβδος ισορροπεί. Δίνεται το μέτρο της επιτάχυνσης της βαρύτητας g=10 m/s2.

 

A)  Να βρείτε τη φορά του B1, τη φορά του Β2 και τη μάζα της ράβδου, αν ξέρετε ότι η συμβατική φορά του ρεύματος που διαρρέει το πλαίσιο είναι αριστερόστροφη (αντίθετη της φοράς περιστροφής των δεικτών του ρολογιού) και στη ράβδο έχει φορά από το Κ προς το Λ.

Κάποια στιγμή ανοίγουμε τον διακόπτη δ1 και ταυτόχρονα κλείνουμε τον διακόπτη δ2.  Παρατηρούμε ότι η ράβδος εξακολουθεί να ισορροπεί.

B)  Να βρεθεί η εσωτερική αντίσταση της πηγής.

Κάποια επόμενη στιγμή ανοίγουμε τον διακόπτη δ2 και η ράβδος αρχίζει να κατέρχεται, ευρισκόμενη συνεχώς μέσα στο μαγνητικό πεδίο έντασης Β2.

Γ)  Να υπολογίσετε τη μέγιστη ηλεκτρική ισχύ στον αντιστάτη R1.

Ενώ η ράβδος έχει αποκτήσει οριακή ταχύτητα, κλείνουμε τον διακόπτη δ3.

Δ)  Να υπολογίσετε το μέτρο του ρυθμού μεταβολής της έντασης του ηλεκτρικού ρεύματος στο πηνίο, τη στιγμή που κλείνουμε τον διακόπτη δ3.

Δίνεται μο = 4π10−7 Ν/A2,  για το πηνίο : R3 = 12Ω, μήκος lπ = 20π cm, εμβαδό διατομής μιας σπείρας Απ = 0,1 m2  και Nπ =1000 σπείρες.
E)  Να υπολογίσετε τη μέγιστη τιμή της ενέργειας του μαγνητικού πεδίου του πηνίου.

ΚΑΛΗ ΕΠΙΤΥΧΙΑ

 

 

Δ1)   αριθμός σπειρών πλαισίου Νπλ = 40 m / 4.0,4m = 25     Eεπ = - Ν ΔΦ/Δt = - Ν dB1/dt α2 = - 25 2,5  0,42 = - 10 V    αντίσταση πλαίσίου : Rπλ = 0,05 Ω/m 40 m = 2 Ω 

έχουμε κύκλωμα  με   Eεπ    και  R1  R2  παράλληλη σύνδεση 

  επαγωγικό ρεύμα :  Ι = Εεπ / ( Rπλ + R1 R2 / (R1+R2) )  = 10 V /  (2 +  12 4 / 16 ) Ω = 2 Α    η τάση στα άκρα της ΚΛ είναι :  VΚΛ = Εεπ  -  I Rπλ = 10  -  2  2  =  6 V

  το ρεύμα που διαρρέει την ΚΛ  είναι  iΚΛ = 6V / 4Ω = 1,5Α     ισορροπία ΚΛ :  mg = FL = B2 iΚΛ l =>  m 10 = 2  1,5  1 =>  m = 0,3 kg

 το ρεύμα που διαρρέει τη ράβδο ΚΛ είναι από το Κ προς το Λ  το ρεύμα ου διαρρέει το πλαίσιο είναι αντίθετα με τη κίνηση των δεικτών του ρολογιού  άρα το επαγωγικό Β είναι προς τα έξω  άρα το Β1 που αυξάνεται με τον χρόνο είναι προς τα μέσα   και το Β2  είναι προς τα μέσα για να ισορροπεί η ΚΛ

 

Δ2)  ανοιγουμε τον  δ1  κλείνουμε τον δ2  τότε έχουμε κύκλωμα  με πηγή  και  R1  R2  παράλληλη σύνδεση   Ε = i (r + R1 R2 / (R1+R2) )  =>  8 = 2  (r + 12 4 / 16) =>  4 = r + 3  =>  r = 1 Ω

η ΚΛ ισορροπεί  mg = FL = B2 i2 l  =>  0,3 10 = 2 i2 1  =>  i2 = 1,5 A     VΚΛ = i2 R2 = 1,5  4  = 6 V      i1 = VΚΛ / R1 = 6 / 12 = 0,5 A       i = 0,5 + 1,5  =  2 A 

 

Δ3)  ανοιγουμε τον  δ2    Β2 l v = i (R1 + R2)  =>  2 1 v = i 16  =>  v = 8 i  =>  i = v/8          mg - B2 i l = m a  =>  0,3 10  -  2  v/8  1 = 0,3 a 

    a = 0  =>  vορ = 12 m/s       PR1 = i2 R1 =  v2/64  12  =  3v2/16        PR1,max = 3  122 / 16  = 27 Watt   

 

Δ4)  κλείνουμε τον  δ3     η ΚΛ κατέρχεται με vορ = 12 m/s  το πηνίο αντιδρά  και δεν περνά ρεύμα            L = 4π 10-7  (103)2  0,1 / 0,2π  = 0,2 Η 

  ρεύμα διαρρέρει την ράβδο ΚΛ  και την αντίσταση R1    B2 l vορ  =  i (R1 + R2) =>  2  1  12  =  i (R1 + R2)  =>  i = 24 / 16 = 1,5 A  

 VΚΛ = B2 l vορ  -  i R2  =  2 1 12  -  1,5 4  = 18 V          VΚΛ =  L di/dt  =>  18 V = 0,2 H  di/dt  =>  di/dt = 90 A/s 

 

Δ5)   αργότερα περνά ρεύμα     B2 l v  -  L di3 /dt  =  i2 R2 +  i3 R3        B2 l v  =  i2 R2 +  i1 R1        i2 = i1 + i3       mg  -  B2 l i2  =  m a 

όταν αποκατασταθούν τα ρεύματα  B2 l v  =  i2  ( R2 + R1 R3 / (R1+R3 ) )    

  mg  -  B2 l i2  =  m a = 0  =>    0,3 10  =  2  1 i2  =>  i2 = 1,5 A     

  B2 l vορ  =  i2  ( R2 + R1 R3 / ( R1+R3 ) )   => 2  1  vορ  = 1,5  ( 4 +  12 12 / (12 + 12) )  =>  vορ  = 7,5 m/s

  VΚΛ = B2 l vορ  -  i2 R2  =  2  1  7,5   -  1,5  4  =  15  - 6 =  9 V   

  i3  = VΚΛ / R3  =  9V / 12Ω = 3/4 Α          UL =  0,5 L i32  =  0,5  0,2  0,752  =>   UL = 9/160 J    

 

 

 

 

 

  Α3.
Ε -  L diπ /dt  =  i (r + R)  +  iπ Rπ   (1)        E  =  i (r + R)  +  iλ Rλ   (2)          i = iπ + iλ   (3)
(2) =>  E = i (r + R) + iλ Rλ  =>  E = ( iπ + iλ ) (r + R)  +  iλ Rλ => E =  iπ (r + R)  +  iλ (r + R +Rλ)  (4)
(1) - (2) =>  - L diπ /dt  =  iπ Rπ  -  iλ Rλ  =>  iλ = ( iπ Rπ +  L diπ /dt ) / Rλ   (5)
 
 (4) , (5) =>  E =  iπ (r + R)  +  (r + R + Rλ) ( iπ Rπ +  L diπ /dt ) / Rλ   =>
   =>  E Rλ =  iπ (r + R)Rλ   +  iπ (r + R + Rλ)Rπ  +  L(r + R + Rλ)  diπ /dt  =>
   =>  E Rλ =  iπ { (r + R)Rλ  +  (r + R + Rλ)Rπ }  +  L(r + R + Rλ)  diπ /dt  =>
   =>  E Rλ =  iπ { (r + R)(Rλ + Rπ) + RλRπ }  +  L(r + R + Rλ)  diπ /dt  =>
   => - L(r + R + Rλ)  diπ /dt  =  iπ { (r + R)(Rλ + Rπ) + RλRπ }  -  E Rλ  =>
   => - L(r + R + Rλ)  diπ /dt  = { (r + R)(Rλ + Rπ) + RλRπ } [ iπ  -  E Rλ / { (r + R)(Rλ + Rπ) + RλRπ } ] =>
=>  diπ / [ iπ  - ERλ / { (r + R)(Rλ + Rπ) + RλRπ } ] = - { (r + R)(Rλ + Rπ) + RλRπ } / L(r + R + Rλ) dt  =>
=>  ln { [ iπ  - ERλ / { (r + R)(Rλ + Rπ) + RλRπ } ] / [ - ERλ / { (r + R)(Rλ + Rπ) + RλRπ } ] }  =
      = - { (r + R)(Rλ + Rπ) + RλRπ } / L(r + R + Rλ) t  =>
=>   iπ  -  ERλ / { (r + R)(Rλ + Rπ) + RλRπ }   =
      =  - ERλ / { (r + R)(Rλ + Rπ) + RλRπ }   e - { (r + R)(Rλ + Rπ) + RλRπ } / L(r + R + Rλ) t  =>
=>   iπ (t)  =  ERλ / { (r + R)(Rλ + Rπ) + RλRπ }  ( 1 -  e - { (r + R)(Rλ + Rπ) + RλRπ } / L(r + R + Rλ) t )  
 
      diπ / dt =   ERλ / L(r + R + Rλ)   e - { (r + R)(Rλ + Rπ) + RλRπ } / L(r + R + Rλ) t    
 
(5) =>  iλ = ( iπ Rπ +  L diπ /dt ) / Rλ  = 
   =  ERπ / { (r + R)(Rλ + Rπ) + RλRπ }  ( 1 -  e - { (r + R)(Rλ + Rπ) + RλRπ } / L(r + R + Rλ) t )   +
       +  E / (r + R + Rλ)   e - { (r + R)(Rλ + Rπ) + RλRπ } / L(r + R + Rλ) t   =
   =  ERπ / { (r + R)(Rλ + Rπ) + RλRπ }   +
     +  [ E / (r + R + Rλ)  -  ERπ / { (r + R)(Rλ + Rπ) + RλRπ } ]  e - { (r + R)(Rλ + Rπ) + RλRπ } / L(r + R + Rλ) t   =
   =  ERπ / { (r + R)(Rλ + Rπ) + RλRπ }   +
     + E { (r + R)(Rλ + Rπ) + RλRπ  -  (r + R + Rλ)Rπ } / (r + R + Rλ) { (r + R)(Rλ + Rπ) + RλRπ }
  e - { (r + R)(Rλ + Rπ) + RλRπ } / L(r + R + Rλ) t   =
   =  ERπ / { (r + R)(Rλ + Rπ) + RλRπ }   +
     + E { (r + R)Rλ + (r + R)Rπ + RλRπ  -  (r + R)Rπ - RλRπ } / (r + R + Rλ) { (r + R)(Rλ + Rπ) + RλRπ }
  e - { (r + R)(Rλ + Rπ) + RλRπ } / L(r + R + Rλ) t   =>
iλ (t)  =  ERπ / { (r + R)(Rλ + Rπ) + RλRπ }   +
     + E (r + R)Rλ / (r + R + Rλ){ (r + R)(Rλ + Rπ) + RλRπ }  e - { (r + R)(Rλ + Rπ) + RλRπ } / L(r + R + Rλ) t  
 
A1. (δ)    Βκυκλ. = 10-7 2π i/R          Biot - Savart       dB = 10-7 i dl/R2 ∙ ημ90° 
               B(O) = ΣdB = 10-7 i Σdl/R2 ∙ ημ90° = 10-7 i R φ /R2 = 10-7 i φ/R        
Α2. (γ)  Τ=8s   ω = 2π/8 = π/4 rad/s      υ(t) = 10π ημ(π/4.t)     x(t) = - 40 συν(π/4.t) = 40 ημ(π/4.t + 3π/2)
Α3. (α) (iv)  (β) (iii)   
Α4.  (δ)
G M1 M2 / (r1 + r2)2  =  M1 v12 / r1  =  M2 v22 r2  =>  M1  ω2 r1  =  M2  ω2 r2  =>  M1  r1  =  M2  r2  =>    M1  r1  =  ½ M1  r2  =>  r1  =  ½  r2  =>   2 r1 =  r2                                
     ο κυανούς Β  εκπέμπει ακτινοβολία μεγαλύτερης συχνότητας από τον αστέρα Α   άρα μικρού μήκους κύματος  συνεπώς  έχει  υψηλότερη θερμοκρασία στην επιφάνειά του  σε σχέση με τον ερυθρό αστέρα Α    
                      διότι   λ . Τ = σταθερά       
  L1 = M1 v1 r1  =  M1 ω r12                       L2 = M2 v2 r2  =  M2 ω r22  =  ½ M1 ω  4 r12 =  2 L1        
       Μ1 >  Μ2     =>    r1 < r2    =>   L1 < L2  

 

Α5.    (α) Λ  Ν = 17∙10-19 C / 1,6∙10-19 C = 10,625 ηλεκτρόνια  ΟΧΙ ΑΚΕΡΑΙΟΣ ΑΡΙΘΜΟΣ ,     (β) Λ ,      (γ) Σ ,      (δ) Λ     (ε) Λ  Pμέση = iεν2 R => 10 Watt = iεν2 10 Ω  => iεν2 = 1 => iεν = 1 Α =>  i0  = √2 Α  =>  i(t) = √2 ∙ ημ(5πt)

 

      Β3.       Λ Υ Σ Η     (β)

 

 

 

 

 

 

      Β2.       Λ Υ Σ Η 


 

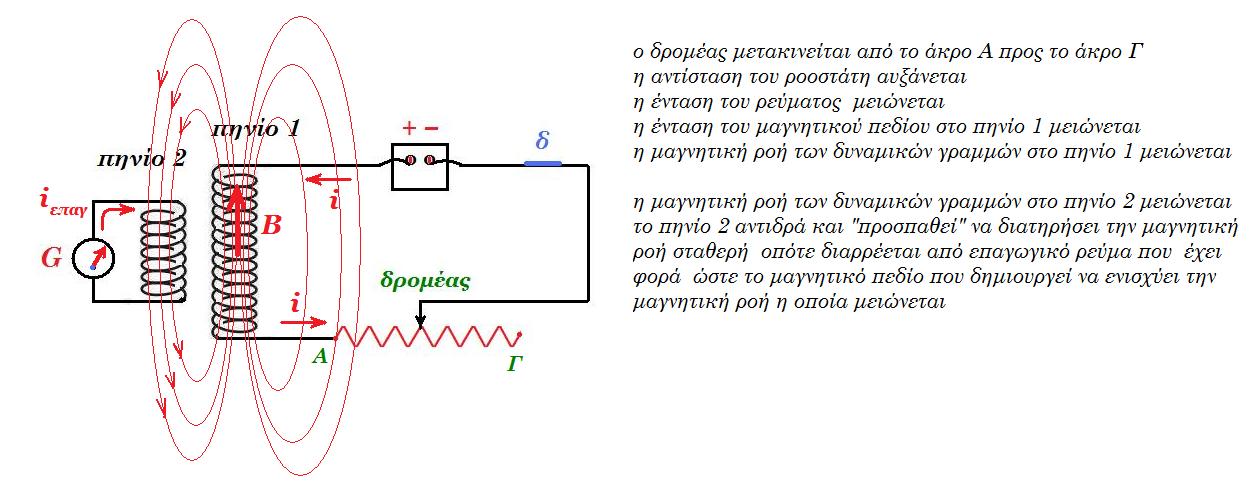
     Β1.         Λ Υ Σ Η

  ωΑ2 = k/m = 4π2 fA2 k/m            ωΒ2 = 4k/m            ωΓ2 = k/4m              ωΔ2 = 2k/m    

    fA = 1/2π √(k/m)                                          fΒ = 1/2π √(4k/m)  = 1/π √(k/m)    

   fΓ = 1/2π √(k/4m)  =  1/4π √(k/m)                         fΔ = 1/2π √(2k/m) 

...........................................................................................................................................

ΘΕΜΑ  Γ

Γ1.    ο μεταγωγέας  δ  είναι στη θέση Ζ :    

η ράβδος διαρρέεται από ρεύμα  i = E / (R1 + R3)  (1)   και είναι μέσα σε ομογενές μαγνητικό πεδίο Β  άρα δέχεται δύναμη Laplace  FL = B . i . l  (2)   

    ισορροπία ράβδου   ΣF = 0  => Τ1 - FL - Tτρ = 0   => Τ1 - FL -  μs . m1 . g  = 0   (3)     

    ισορροπία  Σ2   m2 . g = T2  =>  0,5 . 10 = T2  =>  T2 = 5 N   (4)       

    ισορροπία τροχαλίας  ( ροπές )  T1 . r1  =  T2 . r2  =>   T1 . r1  =  5 N . 2.r1  =>  T1  =  10 N  (5)  

  (3), (4), (5)  =>  10  -  FL  -  0,5 . 0,2 . 10  =  0  =>  FL  =  9 N  (6)   

       (2), (6)  =>  9 N = 2 T . i . 1 m  =>  i  =  4,5 A        

   η  (1)  =>   R1 + R3  =  E / i  =>      R3  =  E / i  - R1  =  9 / 4,5  -  1  =>  R3  =  1 Ω     

  

                μελέτη της κίνησης  ράβδου και σώματος Σ2   

 σώμα Σ2 :  ΣF = m2 α2  =>  m2 g  - Τ2  =  m2 α2  => Τ2  =  0,5 10  -  0,5 α2 =>  Τ2 = 5 - 0,5.α2  (1)   

 τροχαλία  ( ροπές )   T1 . r1  =  T2 . r2  =>   T1 . r1  =  Τ2 . 2.r1  =>  T1 = 2 Τ2 =  10 - α2   (2) 

 ράβδος :  ΣF = m1 α1  =>  Τ1 - FL - Tτρ = m1 α1  =>   Τ1  -  Β i l  -  μs m1 g  = m1 α1  =>

              =>   Τ1  =  2 . i . 1  +  0,5 . 0,2 . 10  +  0,2 . α1 =>   Τ1  =  2.i  +  1  +  0,2 . α1   (3) 

νόμος του Ohm : Εεπαγ = i (R2 +R3) => Β υ1 l  =  i  (R2 +R3)  => 2 υ1 1 = i (1+1)  =>  υ1 = i 

        επειδή  r2 = 2.r1  =>   ω r2 =  ω 2.r1=>  υ2 = 2.υ1  =>  dυ2/dt = 2 . dυ1/dt  =>   α2 = 2.α1    

(3) =>(2)  Τ1  =  2.i  +  1  +  0,2 . α1  =>   10 - α2  =  2.i  +  1  +  0,2 . α1 => 

    =>  10 - 2α1 =  2.υ1  +  1  +  0,2 . α1  =>  - 2,2.α1  =  2.υ1 -  9  =>  α1  =  - 10/11.υ1 +  45/11     

η ράβδος κινείται επιταχυνόμενη     η ταχύτητάς της αυξάνεται οπότε η επιτάχυνσή της ελαττώνεται   και   κάποια στιγμή θα μηδενισθεί   οπότε   η ράβδος θα αποκτήσει σταθερή ταχύτητα υορ = 45/11 . 11/10 = 4,5 m/s 

μαθηματική ανάλυση :

 dv/dt = -10/11 v + 45/11  =>  dv/dt = -10/11 ( v - 4,5 ) =>  dv /(v - 4,5) = -10/11 dt  =>

  =>   ln [ (v - 4,5) / (- 4,5) ]  =  -10/11 t  =>   v - 4,5  =  - 4,5 e-10/11 . t   =>

 =>   v(t)  =  4,5 ( 1 - e-10/11 . t )   ταχύτητα ράβδου ΚΛ     v(0) = 0

a = dv/dt  =>  a(t)  =  45/11 e-10/11 . t    επιτάχυνση ράβδου ΚΛ   a(0) = 45/11 m/s2   αρχική επιτάχυνση ράβδου 

 i(t) = v(t)  = 4,5 ( 1 - e-10/11 . t )     i(0) = 0      ένταση ρεύματος που διαρρέει την ράβδο ΚΛ      

 FL(t)  = B l i =  2  1  4,5 ( 1 - e-10/11 . t ) =>  FL(t) = 9 ( 1 - e-10/11 . t )    FL(0) = 0  

 Τ2  =  5 - 0,5.α2  = 5 - 0,5 . 2 . 45/11 e-10/11 . t  => Τ2 = 5 - 45/11 e-10/11.t 

 T1 = 2 Τ2  =>  Τ1 = 2 ( 5  -  45/11 e-10/11 . t )  => Τ1 = 10 - 90/11 e-10/11 t   

            T1(0)  =  10  - 90/11 = 20/11 N   

 PR = i2 (R3 + R2)  = 4,52 ( 1 - e-10/11 . t )2  2  =>  P(t)  =  9  4,5 ( 1 - e-10/11 . t )2     

 PFL  =  FL v  =  9 ( 1 - e-10/11 . t )   4,5 ( 1 - e-10/11 . t )  =  9  4,5 ( 1 - e-10/11 . t )2    

 PTτρ  =  Ττρ υ  =  μs  m1  g  4,5 ( 1 - e-10/11 . t )  =  0,5  0,2  10  4,5 ( 1 - e-10/11 . t )  =>

         =>   PTτρ(t) =  4,5 ( 1 - e-10/11 . t )  

 dK/dt =  m1  v  a  =  0,2   4,5 ( 1 - e-10/11 . t )   45/11 e-10/11 . t   =>

              =>   dK/dt  =  4,5  9/11 e-10/11 . t  ( 1 - e-10/11 . t )   

 PT1  =  Τ1 υ  =  [ 10  -  90/11 e-10/11 . t ]  4,5 ( 1 - e-10/11 . t )  =>  

            =>    ΡΤ1  =   45  [ 1  -  9/11 e-10/11 . t ]  ( 1 - e-10/11 . t )     

η ράβδος ΚΛ κινείται λόγω της τάσης νήματος Τ1 , που έχει διπλάσιο μέτρο από την τάση νήματος Τ2  η οποία ασκείται στο σώμα Σ2 ,   υπάρχει δύναμη τριβής ,  δύναμη Laplace  οι οποίες είναι αντίρροπες της Τ1  και  η ράβδος έχει ταχύτητα   

PFL  + PTτρ  +  dK/dt  = 

  =  9 4,5 ( 1 - e-10/11 . t )2  +  4,5 ( 1 - e-10/11 . t )  +  4,5  9/11 e-10/11 . t  ( 1 - e-10/11 . t )   =  

  =  4,5 ( 1 - e-10/11 . t )   [  9 ( 1 - e-10/11 . t )  +  1  +  9/11 e-10/11 . t  ]  =    

  =  4,5 ( 1 - e-10/11 . t )   [  10 -  9 e-10/11 . t  +  9/11 e-10/11 . t  ]  =

  =  4,5 ( 1 - e-10/11 . t )   [  10 -  90/11 e-10/11 . t  ]  =  PT1      

 

Γ2.    ο μεταγωγέας  δ  είναι στη θέση Ε :

  ΣF = m2 α2   =>   m2 g  -  Τ2  =  m2 α2  =>   0,5 10  -  Τ2  =  0,5 2  => Τ2  =  4 Ν     

  T1 . r1  =  T2 . r2  =>  T1 . r1  =  4 N . 2.r1  =>  T1  =  8 N   

 η ράβδος κινείται  μέσα σε μαγνητικό πεδίο  κάθετα στις δυναμικές γραμμές,   στα ηλεκτρόνια της ράβδου ασκούνται δυνάμεις Lorenz  με συνέπεια να μετακινούνται προς το άκρο Κ    το οποίο φορτίζεται αρνητικά (-)  οπότε το άκρο Λ φορτίζεται θετικά (+),  έτσι η ράβδος γίνεται πηγή ηλεκτρικού ρεύματος,  στα άκρα ΚΛ εμφανίζεται επαγωγική τάση   Εεπαγ = Β . υ1 . l        

  νόμος του Ohm  για κλειστό κύκλωμα :  Εεπαγ =  i (R2 +R3)  =>  Β υ1 l  =  i (R2 +R3)      

  η τροχαλία περιστρέφεται με γωνιακή ταχύτητα  ω = αγων .t   τότε  υ1 = ω . r1  &  υ2 = ω . r2    επειδή   r2 = 2.r1  τότε  υ2 = 2.υ1 => α2 = 2.α1   ( επιταχύνσεις )   άρα  α1 = 1 m/s2   

  η ράβδος δέχεται δύναμη  Laplace  FL = B . i . l    &  τάση νήματος  Τ1 = 8 Ν 

     ΣF = Τ1 - FL - Tτρ =  m1 α1  =>  8  - FL -  0,5 0,2 10  =  0,2 1 =>  FL = 6,8 Ν 

 από τη σχέση    FL = B i l =>   6,8 Ν  = 2 Τ  i  1 m  =>  i  =  3,4 A       

  η τάση στα άκρα της R2  :  V2  =  VΓΕ  =  3,4 Α  1 Ω  =>    VΓΕ  =  3,4 Volt    

 από τη σχέση    Β υ1 l  =  i (R2 +R3)   =>  υ1  =  3,4 (1 + 1) / 2.1  =>  υ1 = 3,4 m/s       

 

Γ3.   σώμα Σ2 :   ΣF = 0  =>  Τ2 - m2 g = 0  =>  Τ2  = 5 Ν                

        τροχαλία  ( ροπές )   T1 . r1  =  T2 . r2  =>   T1 r1  =  5 N  2.r1  => T1 = 10 N 

ράβδος :  ΣF = 0  =>  Τ1 - FL - Tτρ = 0 =>  Τ1  -  Β i l  -  μs m1 g  = 0  => 10  -  2 i 1 -  0,5 0,2 10 = 0 =>

                              =>   i  =  4,5 A    

νόμος Ohm : Εεπαγ =  i (R2 +R3)  =>  Β  υορ l  =  i (R2 +R3)  =>  2 υορ 1 =  4,5 .(1+1) => υορ = 4,5 m/s  

επειδή  r2 = 2.r1    τότε  υ2 = 2.υορ = 9 m/s      το Σ2 θα κινείται με οριακή ταχύτητα   υορ(2)  =  9 m/s  

 

Γ4.  η τροχαλία κάνει  Ν = 9 περιστροφές   τότε  θ = Ν 2π rad  =  18.π rad      

υορ(2)  =  ω  r2  =>  ω = 9 m/s / 0,1 m =>  ω = 90 rad/s       ω = θ / t  =>  t = 18.π / 90  =>  t = 0,2.π s 

η ράβδος διανύει διάστημα   x1  =  υορ  t  =  4,5 m/s  0,2.π s  =>  x1 = 0,9.π m          

το σώμα Σ2  διανύει διάστημα   x2  =  υορ(2)  t  =  9 m/s  0,2.π s  =>   x2 = 1,8.π m = h 

 Κ = ½ m2 υορ(2)2  =  ½  0,2 kg   (9 m/s)2  =  8,1 J 

  U(Σ2)  =  m2  g  h  =  0,5 kg  10 m/s2  1,8.π m  =>   U(Σ2) = 9.π Joule = T2  x2 = |WT2|       

  WT1  =  T1  x1  =  10 N  0,9.π m  =>   WT1 = 9.π Joule   

  WTτρ  =  Tτρ x1  =  μs m1 g  x1  =  0,5  0,2 10   0,9.π  =>   WTτρ = 0,9.π Joule    

  FL = B i l =  2 Τ 4,5 Α 1 m = 9 N       WFL = FL x1 =  9 N 0,9.π m  =>  WFL = 8,1.π Joule 

  Qθερμ =  i2 (R2 + R3)  t  =>  Qθερμ =  4,52 (1 + 1)  0,2.π  =>   Qθερμ = 8,1.π Joule 

παρατηρούμε ότι καθώς κατεβαίνει το σώμα Σ2 η δυναμική βαρυτική ενέργεια μειώνεται κατά 9π J     η ράβδος κερδίζει ενέργεια 9.π J λόγω το έργου που παράγει η τάση Τ1 του νήματος        η οποία ενέργεια καταναλώνεται στις τριβές 0,9.π J    και  στην δύναμη Laplace 8,1.π J     η οποία ισούται με την θερμότητα λόγω φαινομένου Joule πάνω στις αντιστάσεις R2  και R3   

 

 

ΘΕΜΑ  Δ

Δ1.  εξίσωση έντασης του ηλεκτρικού πεδίου  Ε(x,t) = E0 ημ 2π(ft - x/λ) = 300· ημ 2π(1018 t - x/λ )  (S.I.) 

 f  = 1018 Hz     c = λ f  =>  λ = c / f  = 3·108m/s / 1018 Hz =>  λ = 3·10-10m = 0,3 nm < 400 nm (ιώδες)  aκτίνες Χ

        B0  =  Ε0 / c  =>   Β0  =  300 V/m  /  3·108 m/s  =  10-6 Τ   

 εξίσωση της έντασης του μαγνητικού πεδίου   Β(x,t) = B0 ημ 2π( ft - x/λ ) = 10-6· ημ 2π(1018 t - 1010 x/3 )   (S.I.) 

 

Δ2.  t=2·10-18s     Ε(x) =  300·ημ 2π(1018·2·10-18 - 1010 x/3 ) =  300·ημ (4π - 2π·1010·x/3) =>

                           Ε(x) = - 300·ημ (2π·1010·x/3)  

 

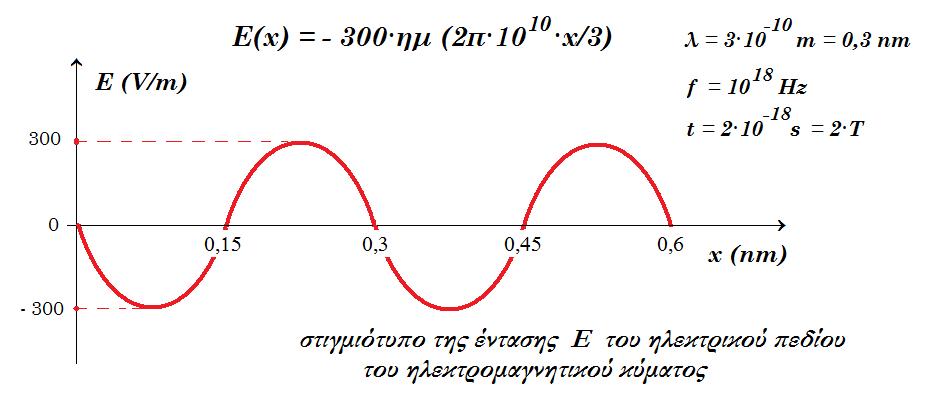
Δ3.  προσπίπτον Η/Μ κύμα :  Β(x,t) = B0  ημ 2π( ft - x/λ ) = 10-6·ημ 2π(1018 t - 1010 x/3 )  (S.I.) 

      ανακλώμενο Η/Μ κύμα : Β'(x,t) = B0 ημ (2πft + 2πx/λ + π) = 10-6·ημ (2π 1018 t + 2π 1010 x/3 + π)  (S.I.) 

      στάσιμο Η/Μ κύμα :  Β"(x,t) = 2 B0 συν (2πx/λ + π/2) ημ (2πft + π/2) = - 2B0 ημ(2πx/λ) συν(2πft) 

                                                = - 2 .10-6· ημ(2π .1010 x/3) συν(2π .1018 t)   (S.I.)      

                                    λ/4 + 3λ/2 = 7λ/4 = 21/4·10-10m

                       κ      δ      κ      δ      κ      δ      κ      δ      κ      δ  Ο μεταλλική επιφάνεια         

 

απόδειξη :                

Β(x,t)  + Β'(x,t)  =  B0  ημ (2πft  -  2πx/λ)  +   B0 ημ (2πft + 2πx/λ + π)  = 

  =  2B0  ημ ( 2πft - 2πx/λ +  2πft + 2πx/λ + π ) / 2    συν ( 2πft - 2πx/λ -  2πft - 2πx/λ - π ) / 2  =

  =  2B0  ημ ( 4πft + π ) / 2   συν ( - 4πx/λ - π ) / 2  =  2B0  ημ ( 2πft + π/2 )  συν ( - 2πx/λ - π/2 )  =   

  =  2B0  συν ( 2πx/λ + π/2 )  ημ ( 2πft + π/2 )  =

  = 2B0  [ συν(2πx/λ) συν(π/2) - ημ(2πx/λ) ημ(π/2) ]  [ ημ(2πft) συν(π/2)+ συν(2πft)  ημ(π/2) ] =  

  = 2B0 [ - ημ (2πx/λ) ] [ + συν (2πft) ] = - 2B0 ημ(2πx/λ)  συν(2πft)      

ημα + ημβ = 2 ημ(α + β)/2  συν(α - β)/2

 

Δ4.      E = h f   =  6,6 10-34 J.s  1020 Hz  =  6,6 10-14 J     ενέργεια προσπίπτοντος φωτονίου     

     λ = c / f  = 3·108m/s / 1020 Hz =>  λ = 3·10-12m  =  3 pm 

    φαινόμενο Compton :   λ' - λ  =  h / mc ( 1 - συν90° ) =>

=> λ' - 3 10-12 m = 6,6 10-34 / ( 9 10-31  3 108 ) ( 1 - 0 ) = 0,24 10-11 m  => λ' - 3 10-12 m = 2,4 10-12 m  =>

=>  λ'  =  5,4 10-12 m  = 5,4 pm        

    f ' = c / λ'  =  3 108 / 5,4 10-12  =  0,55 1020 Hz    συχνότητα σκεδαζομένου φωτονίου 

  ενέργεια σκεδαζομένου φωτονίου :  E' = h f '  = 6,6 10-34 J.s   0,55 1020 Hz = 3,63 10-14 J  = 2,27 .103  eV  

διατήρηση ορμής :  pe,x = E/c =>  pe  συνθ = h / λ   (1)         pe,y = E'/c =>  pe  ημθ = h / λ'   (2)  

          (2) / (1) =>  εφθ  =  λ / λ' =  3 pm / 5,4 pm  =>  εφθ  = 0,55     

 

Δ5.       h f  +  eV  =  Ke  + φ  =>   6,6 10-34  6 1014   +  1,6 10-19  1  =  Ke  +  2,4 . 1,6 10-19  =>

               =>  39,6 10-20  + 1,6 10-19 =  Ke  +  3,84 10-19  =>  0,12 10-19  +  1,6 10-19  =  Ke  = 1,72 .10-19 J   

 h f  +  eV  =  Ke  + φ  =>  h f  +  e V0  =   φ  =>   6,6 10-34  6 1014   +  1,6 10-19  V0   = 2,4 1,6 10-19  => 

              =>  3,96 10-19 + 1,6 10-19  V0  =  3,84 10-19  =>  - 0,12 10-19  /  1,6 10-19  = V0 = - 0,12 / 1,6 V = - 0,075 V

f  = c / λ =  3 108 / 5 10-7 =  0,6 1015 Hz  =  6 1014 Hz                   V  =   φ/e  -  h/e  f           f0 = φ/e   

 h f  +  eV  =  Ke  + φ  =>   6,6 10-34  6 1014   +   eV   =   Ke  +   6,25 . 1,6 10-19  =>

               =>  39,6 10-20   + eV   =  Ke  +  10 10-19  =>   40 10-20   + eV   =  Ke  +  10 10-19  =>   4 10-19   +  eV   =  Ke  +  10 10-19  =>   - 6 10-19   +  eV   =  Ke    όση τάση και να βάλουμε τα ηλεκτρόνια δεν βγαίνουν από την επιφάνεια του λευκοχρύσου διότι η ακτινοβολία έχει μικρή συχνότητα    για να βγουν ηλεκτρόνια από την επιφάνεια του λευκοχρύσου  πρέπει η συχνότητα να είναι :   h f0  =  φ  =>  f0  =  φ / h = 6,25 1,6 10-19 / 6,6 10-34  =>  f0 =  1,5 1015 Hz     λ0 = c / f0 =  3 108 / 1,5 1015 = 2 10-7  m  = 200 10-9 m  = 200 nm  <  400 nm  (ιώδες)          πρέπει η ακτινοβολία να είναι υπεριώδης

 

 

 

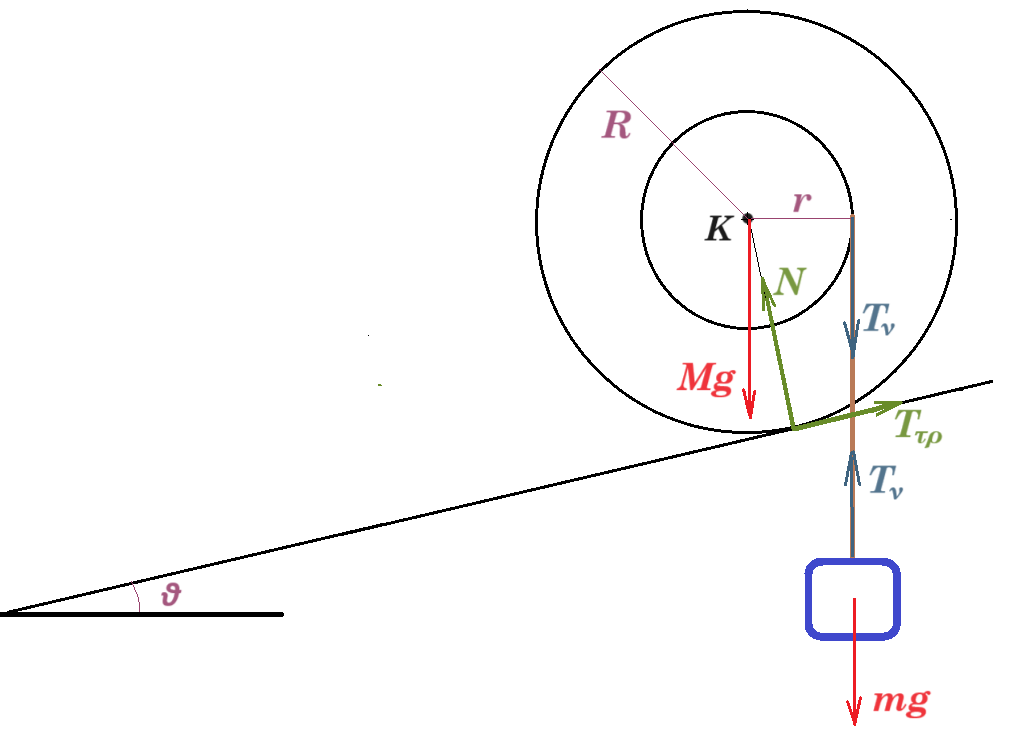       ισορροπία σώματος :   mg = Tν       

  ισορροπία τροχού :  Στ(Κ) = 0  =>  Ττρ R = Τν r  =>  Ττρ R =  Τν R/2  =>  Ττρ = Τν / 2  = mg / 2       

ΣFx = 0  =>  Ττρ  -  Mg ημθ  -  Τν ημθ  =  0   =>  mg / 2  -  Mg  1/10  -  mg  1/10  =  0  =>  M = 4m

ΣFy = 0  =>  N  -  Mg συνθ  -  Τν συνθ  =  0  =>  N  -  4mg συνθ  -  mg συνθ  =  0 =>  N = 5mg συνθ

  μσ  =  Ττρ / Ν =   1/2 mg  /  5 mg συνθ  =  1 / 10συνθ  =  1/10 / συνθ  =  ημθ / συνθ  =>  μσ = εφθ