Ταλάντωση - ελαστική κρούση - οριζόντια βολή

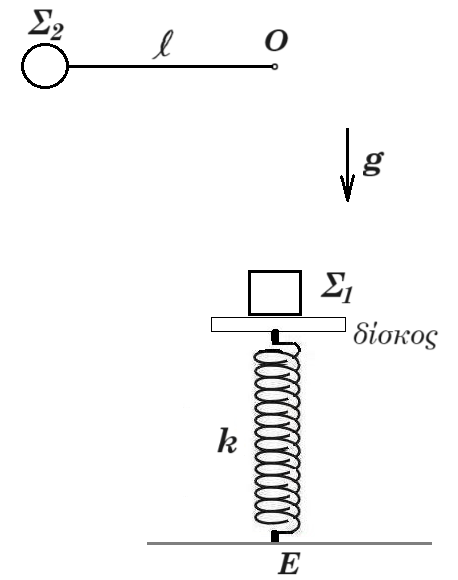
Σώμα Σ₁ μάζας m₁ = 3kg ισορροπεί πάνω σε δίσκο  μάζας Μ = 1kg. Ο δίσκος είναι στερεωμένος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 400 N/m ενώ το κάτω άκρο του ελατηρίου είναι στερεωμένο στο σημείο Ε του οριζόντιου επιπέδου. Στην ίδια κατακόρυφο με τον άξονα του ελατηρίου ισορροπεί ακίνητο σώμα Σ₂ μάζας m₂ που είναι δεμένο στο κάτω άκρο κατακόρυφου, αβαρούς και μη εκτατού νήματος μήκους l το άλλο άκρο του οποίου είναι στερεωμένο σε σημείο Ο που απέχει απόσταση από το Ε  (ΟΕ) = 1 m. Την χρονική στιγμή t₀ προσδίδουμε κατακόρυφη ταχύτητα μέτρου υ₀ με φορά προς τα πάνω στο σύστημα Σ₁ - δίσκος  και το σύστημα των δυο σωμάτων εκτελεί έναν αριθμό ταλαντώσεων στην διάρκεια των οποίων οριακά δεν χάνεται η μεταξύ τους επαφή. Την χρονική στιγμή t₁ αφήνουμε το Σ₂ από θέση που το νήμα είναι τεντωμένο και οριζόντιο. Την χρονική στιγμή t₂ που το Σ₂ διέρχεται για πρώτη φορά από την κατακόρυφη θέση με ταχύτητα μέτρου υ₂ = 2 m/s κόβεται το νήμα και το Σ₂ συγκρούεται ελαστικά με το Σ₁ με αποτέλεσμα τα σώματα Σ₁ και Σ₂ να εκτελούν οριζόντια βολή και να προσγειώνονται σε σημεία του οριζόντιο επιπέδου που το ευθύγραμμο τμήμα που ορίζουν έχει ως μέσο το σημείο Ε. Θεωρήστε τα σώματα σημειακά αντικείμενα και τις αντιστάσεις από τον αέρα αμελητέες. Δίνεται g = 10 m/s².
Να υπολογίσετε :
1) το μέτρο της ταχύτητας εκτόξευσης υ₀       2) την μάζα m₂ του σώματος Σ₂       3) το φυσικό μήκος του ελατηρίου (l₀) 

4) το πλάτος της ταλάντωσης που θα εκτελέσει ο δίσκος μετά την κρούση των Σ₁ και Σ₂.

   θετική φορά προς τα πάνω        

ισορροπία  Σ₁ - δίσκου :  ΣF =  0  =>  k Δl = (m₁ + M) g  =>  400 Δl  = 4 10  => Δl = 0,1m  συσπείρωση ελατηρίου 

  k = (m₁ + M) ω²  =>  400 = 4 ω²  =>  ω = 10 rad/s        

ταλάντωση  Σ₁ - δίσκου :  ΣF = (m₁ + M) a  =>  - (m₁ + M) g  + F_ελατ = - k x  => F_ελατ = - k x + (m₁ + M) g = 40 - 400 x        

ταλάντωση  Σ₁  :  ΣF = m₁ a  = - m₁ ω² x = - D₁ x =>  - m₁ g  + N + F_ελατ = - D₁ x => - 30  + N + 40 - 400 x = - 300 x =>   N + 10  = 100 x   =>   N  = 100 x - 10            Ν = 0   τότε  x = 0,1 m = A

    x = 0,1 ημ(10t)       v = 1 συν(10t)       α = - 10 ημ(10t)           t = 0  =>  v₀ = 1 m/s 

   m₂ g l  =  0,5 m₂ v₂²  =>  2 g l = v₂²  =>  l = 4 / 20 = 0,2 m    (2)                

  όταν γίνεται η ελαστική κρούση  το Σ₁  βρίσκεται σε ακρότατη θέση ταλάντωσης  ( v₁ = 0 )   διότι μετά θα εκτελέσει οριζόντια βολή προς τα δεξιά με ταχύτητα  υ₁' =  2 v₂ m₂ / (m₂ + m₁) και  θα διανύσει οριζόντια απόσταση  χ₁ = υ₁' t 

το Σ₂ μετά την ελαστική κρούση θα έχει ταχύτητα   v₂' =  v₂ (m₂ - m₁) / (m₂ + m₁)  =>  v₂' = 2 (m₂ - 3) / (m₂ + 3)     και  θα διανύσει οριζόντια απόσταση  χ₂ = υ₂' t   από το ίδιο ύψος άρα στον ίδιο χρόνο

  επειδή  χ₁ = χ₂ => υ₁' = - υ₂' =>   2 v₂ m₂ / (m₂ + 3)  =  - 2 (m₂ - 3) / (m₂ + 3)  =>  2 m₂  =  - m₂ + 3  =>  m₂ = 1 kg  

αν  άνω ακραία θέση :     l₀  + l = (OE) = 1m  =>   l₀  +  0,2m = 1m  =>  l₀ = 0,8m 

          h = l₀ = 0,5 g t² =>  0,8 = 0,5 10 t² =>  t = √0,16 s = 0,4 s

αν  κάτω ακραία θέση :   ( l₀ -  2 Δl ) + l = (OE) = 1m  =>  ( l₀ -  0,2m ) +  0,2m = 1m  =>  l₀ = 1m

        h = l₀ -  2 Δl = 0,5 g t² =>  0,8 = 0,5 10 t² => t = √0,16 s = 0,4 s

 όταν συγκρούονται τα Σ₁ Σ₂  ο δίσκος είναι στιγμιαία ακίνητος  στην άνω ακραία θέση  ή  στην κάτω ακραία θέση  

μετά  θα εκτελέση  Α.Α.Τ.       

ισορροπία δίσκου :    ΣF =  0  =>  k Δl' =  M g  =>  400 Δl'  = 1 10  => Δl' = 1/40 m = 0,025 m  συσπείρωση ελατηρίου 

      k =  M ω'²  =>  400 = 1 ω'²  =>  ω' = 20 rad/s        

αν είναι   στην άνω ακραία θέση  τότε    l₀ =  0,8m   το ελατήριο έχει το φυσικό του μήκος   ο δίσκος είναι στιγμιαία ακίνητος υψηλότερα κατά Δl' = 0,025 m       x = 0,025 ημ(20t + π/2)         v = 0,5 ημ(20t + π/2)           a = - 10 ημ(20t + π/2)  

αν είναι   στην κάτω ακραία θέση  τότε    l₀ =  1m   το ελατήριο είναι συσπειρωμένο κατά  2 Δl = 0,2m    ο δίσκος είναι στιγμιαία ακίνητος υψηλότερα κατά  2 Δl - Δl' = 0,2m - 0,025m = 0,175m       x = 0,175 ημ(20t + π/2)       v = 3,5 ημ(20t + π/2)           a = - 70 ημ(20t + π/2)