ΘΕΜΑ  Α

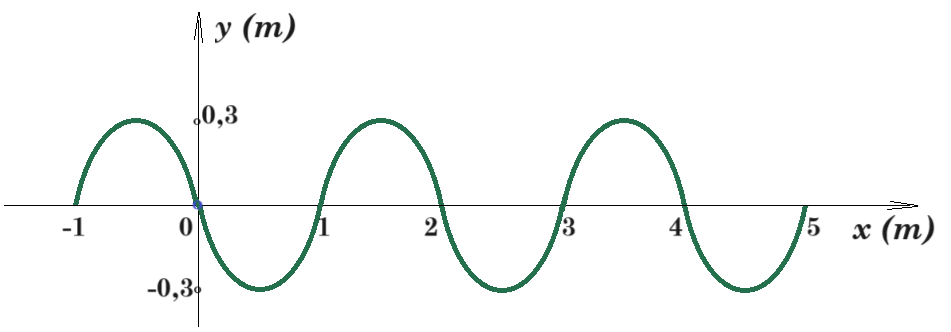
Κατά μήκος ενός γραμμικού ελαστικού μέσου, διαδίδεται ένα εγκάρσιο αρμονικό πλάτους Α=0,3m και στο σχήμα δίνεται το διάγραμμα της φάσης της απομάκρυνσης των  διαφόρων σημείων του μέσου, σε συνάρτηση με την θέση x (φ=f(x)) τη χρονική στιγμή t₁.

α)  Το κύμα διαδίδεται προς τα δεξιά (θετική φορά του άξονα) ή προς τα αριστερά;

β)  Να υπολογίσετε το μήκος του κύματος καθώς και την θέση x₁, όπου φτάνει το κύμα τη στιγμή t₁.

γ)  Να σχεδιάσετε την γραφική παράσταση της φάσης  (φ=f(x)) της απομάκρυνσης, την χρονική στιγμή t₂=t₁+2Τ, όπου Τ η περίοδος ταλάντωσης των σημείων του μέσου.

δ)  Αν η περίοδος ταλάντωσης των σημείων του μέσου είναι Τ=1s, ενώ t₁=2s:

    α)  Να βρεθεί η εξίσωση του κύματος.

    β)  Να σχεδιάσετε το στιγμιότυπο του κύματος τη χρονική στιγμή t₂=1s.

                  ΘΕΜΑ  Β

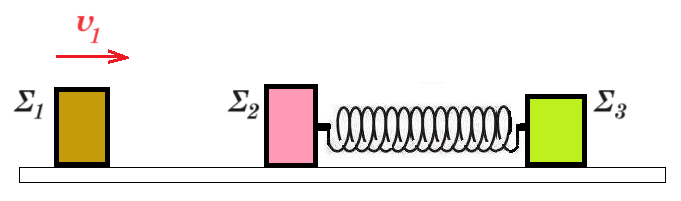
Αρχικά τα σώματα Σ₂ , Σ₃   με μάζες  m₂ = 2kg  m₃ = 4kg  είναι ακίνητα επάνω στο λείο οριζόντιο επίπεδο  δεμένα στα άκρα οριζοντίου ιδανικού ελατηρίου  σταθεράς  k = 4800 N/m  το οποίο είναι στο φυσικό του μήκος.  Σώμα Σ₁ μάζας  m₁ = 1kg  κινούμενο με οριζόντια ταχύτητα  υ₁ = 9 m/s  συγκρούεται κεντρικά ελαστικά με το σώμα Σ₂.  Βρείτε την μέγιστη συσπείρωση του ελατηρίου.

α)  Βρείτε την μέγιστη συσπείρωση του ελατηρίου.

β)  Βρείτε τον ρυθμό μεταβολής της κινητικής ενέργειας του Σ₃ τη στιγμή που το Σ₂ έχει ταχύτητα  + 4 m/s.

                  ΘΕΜΑ  Γ

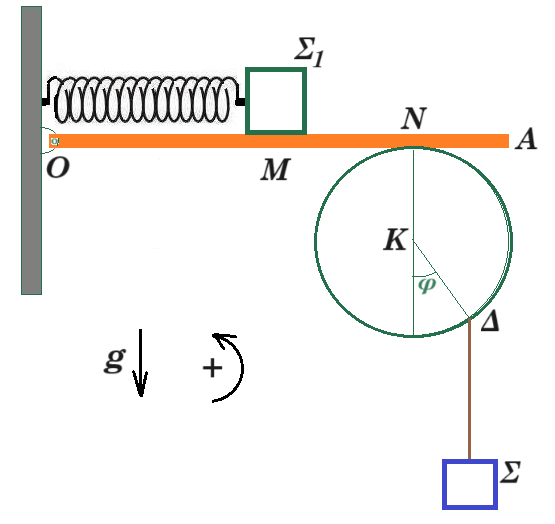
Ομογενής, λεπτή ράβδος ΟΑ μήκους L = 1m και μάζας Μ = 6 kg έχει το άκρο της Ο αρθρωμένο σε κατακόρυφο τοίχο χωρίς να αναπτύσονται τριβές. Κάτω ακριβώς από την ράβδο και σε επαφή με αυτήν στο σημείο Ν βρίσκεται δίσκος ακτίνας R ο οποίος μπορεί να στρέφεται γύρω από οριζόντιο άξονα που διέρχεται από το κέντρο του Κ χωρίς να αναπτύσσονται τριβές. Η απόσταση ΟΝ ισούται με d = 0,75 m. Σε σημείο Δ του δίσκου είναι δεμένο κατακόρυφο αβαρές και μη εκτατό νήμα που στο άλλο του άκρο είναι δεμένο σώμα Σ μάζας m = 2 kg και το ευθύγραμμο τμήμα ΚΔ σχηματίζει γωνία φ = 30⁰ με την κατακόρυφο. Ιδανικό, οριζόντιο ελατήριο σταθεράς k έχει το αριστερό του άκρο στερεωμένο στον κατακόρυφο τοίχο και στο δεξί στου άκρο είναι δεμένο σώμα Σ₁ μάζας m₁ = 3 kg το οποίο εκτελεί απλή αρμονική ταλάντωση πάνω στην ράβδο πλάτους Α = 0,25 m. H θέση ισορροπίας του σώματος Σ₁ συμπίπτει με το μέσο M της ράβδου. Μεταξύ της ράβδου και του δίσκου αναπτύσσεται στατική τριβή με αποτέλεσμα το σώμα Σ να παραμένει συνεχώς ακίνητο. Όλα τα σώματα βρίσκονται στο ίδιο κατακόρυφο επίπεδο. Δίνεται g = 10 m/s².
Να υπολογίσετε την ελάχιστη τιμή του συντελεστή στατικής τριβής μεταξύ ράβδου και δίσκου ώστε το σώμα Σ να παραμένει συνεχώς ακίνητο.

                  ΘΕΜΑ  Β

a)    v₁' = v₁ (m₁ - m₂)/(m₁ + m₂) = 9 (1 - 2)/(1 + 2) = - 3 m/s  

        v₂' = 2 v₁ m₁/(m₁ + m₂) = 2 9 1/3 = + 6 m/s 

το Σ₂ μετά την ελαστική κρούση ασκεί δύναμη στο ελατήριο το οποίο συσπειρώνεται  ενώ το Σ₂  δεχόμενο αντίθετη δύναμη από το ελατήριο κινείται προς τα δεξιά επιβραδυνόμενο 

το ελατήριο ασκεί προς τα δεξιά δύναμη στο Σ₃  το οποίο επιταχύνεται  

κάποια στιγμή οι ταχύτητες των Σ₂ Σ₃  θα γίνουν ίσες  έστω  υ₂ = v₃ = v

το σύστημα των Σ₂ Σ₃ ελατηρίου θεωρείται μονωμένο η συνισταμένη των εξωτερικών δυνάμεων ισούται με μηδέν οπότε  διατήρηση ορμής :   m₂ v₂' = m₂ v₂ + m₃ v₃   (1)  =>  m₂ v₂' = m₂ v + m₃ v  => 2 6 = 2 v + 4 v => v = 2 m/s

διατήρηση ενέργειας :  ½ m₂ (v₂')² =  ½ m₂ v₂²  +  ½ m₃ v₃²  +  ½ k x²    (2)   =>

  =>   ½ m₂ (v₂')² =  ½ m₂ v²  +  ½ m₃ v²  +  ½ k x²   =>

  =>  2 6² =  2 2²  +  4 2²  +  4800 x²  => 24 = 2400 x²  => x = 0,1 m   μέγιστη συσπείρωση ελατηρίου

β)     όταν  v₂ = 4 m/s   από (1) =>  m₂ v₂' = m₂ v₂ + m₃ v₃  =>  2 6 = 2 4 + 4 v₃  =>  v₃ = 1 m/s  

από  (2) =>   ½ m₂ (v₂')² =  ½ m₂ v₂²  +  ½ m₃ v₃²  +  ½ k x²  =>  2 6² =  2 4²  +  4 1²  +  4800 x²  => 

  =>  72  -  32  -   4  =  4800 x²  =>   x² = 36 / 4800 = 3 / 400 m²  =>  x = √3 / 20 m 

ρυθμός μεταβολής κινητικής ενέργειας του Σ₃ :  dK₃/dt = m₃ v₃ a₃ = v₃ F_ελατ = v₃ k x = 1 m/s  4800 N/m  √3 / 20 m  =  240√3 J/s 

                  ΘΕΜΑ  Γ

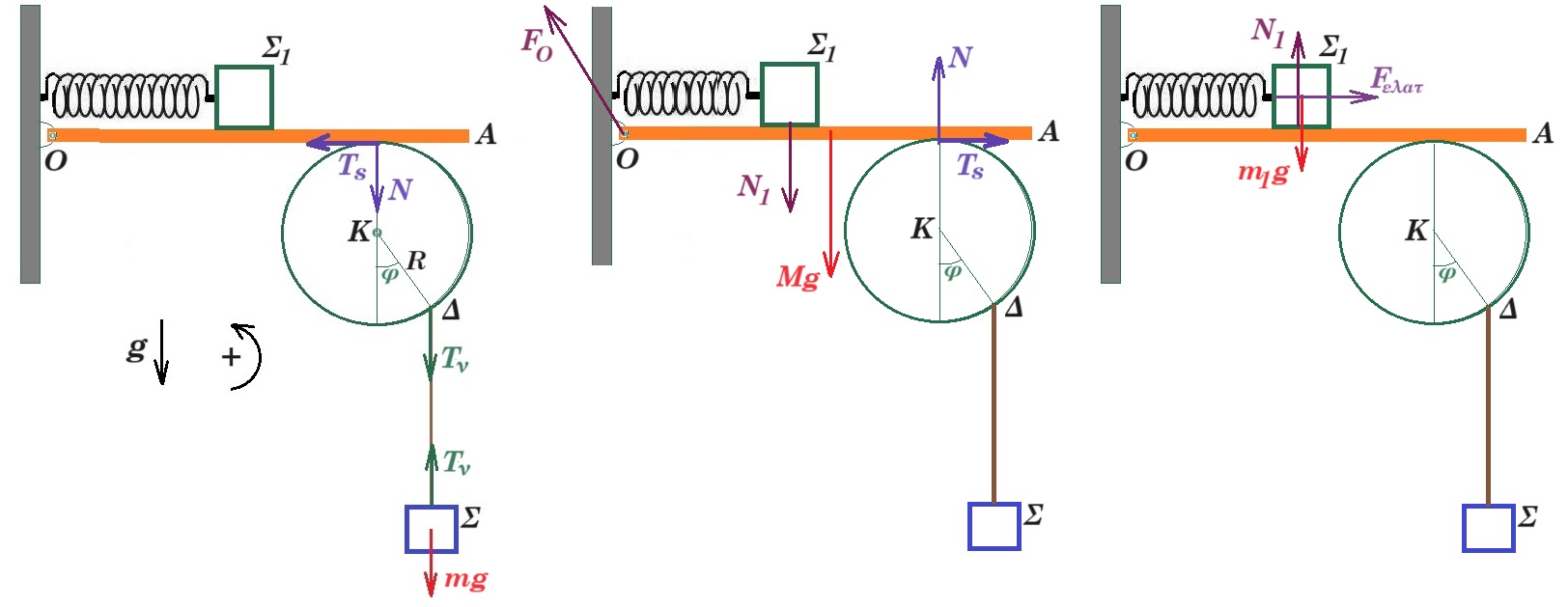
ισορροπία Σ :  T_ν = mg = 20 Ν  

ισορροπία δίσκου :  Στ_(Κ) = 0  =>  T_s R - T_ν R ημ30°  = 0  =>  T_s = T_ν = 10 N                         μ_s ³ T_s / N   

Α.Α.Τ.  Σ₁ :   ΣF_y = 0  =>  Ν₁ = m₁g = 30 N           ΣF_x = m₁ a  =>  - k x  =  m₁ a  =>  - k x = - 3 ω² x  

ισορροπία ράβδου ΟΑ :  Στ_(Ο) = 0  =>  - Mg L/2  - N₁ (L/2 + x)  + N 3L/4  =  0  =>  - 30  - 30 (0,5 + x)  + N 0,75  =  0  =>

=>  N 0,75  =  45 + 30 x  =>  N  =  60 + 40 x     επειδή   - 0,25 m £  x £ + 0,25 m   τότε  50 Ν £ Ν £ 70 Ν

  N = 50 N     μ_s ³ T_s / N  =  10 / 50 = 0,2                   N = 70 N     μ_s ³ T_s / N  =  10 / 70 = 0,14        

   συνολικά   μ_s ³  0,2    διότι

εάν  Ν = 50 Ν  και   μ_s = 0,1  <  0,14 = 1/7    τότε   T_s  =  μ_s N =  0,1  50 Ν = 5 Ν    οπότε  Στ_(Κ) =  T_s R - T_ν R ημ30°  =  ( 5 - 20  ½ ) R  = - 5 R  διάφορο του μηδενός  οπότε  ο δίσκος  θα περιστραφεί περί τον άξονά του  όπως οι δείκτες του ρολογιού  και το σώμα  Σ θα κινηθεί επιταχυνόμενο προς τα κάτω 

εάν  Ν = 70 Ν  και   μ_s = 0,1  <  0,14 = 1/7    τότε   T_s  =  μ_s N =  0,1  70 Ν = 7 Ν    οπότε  Στ_(Κ) =  T_s R - T_ν R ημ30°  =  ( 7 - 20  ½ ) R  = - 3 R  διάφορο του μηδενός  οπότε  ο δίσκος  θα περιστραφεί περί τον άξονά του  όπως οι δείκτες του ρολογιού  και το σώμα  Σ θα κινηθεί επιταχυνόμενο προς τα κάτω 

εάν  Ν = 50 Ν  και   μ_s = 0,17  >  0,14 = 1/7  αλλά  <  0,2    τότε   T_s  =  μ_s N =  0,17  50 Ν = 8,5 Ν    οπότε  Στ_(Κ) =  T_s R - T_ν R ημ30°  =  ( 8,5 - 20  ½ ) R  = - 1,5 R  διάφορο του μηδενός  οπότε  ο δίσκος  θα περιστραφεί περί τον άξονά του  όπως οι δείκτες του ρολογιού  και το σώμα  Σ θα κινηθεί επιταχυνόμενο προς τα κάτω 

εάν  Ν =70 Ν  και   μ_s = 0,17  >  0,14 = 1/7  αλλά  <  0,2    τότε   T_s  =  μ_s N =  0,17  70 Ν = 11,9 Ν    οπότε  Στ_(Κ) =  T_s R - T_ν R ημ30°  =  ( 11,9 - 20  ½ ) R  =  1,9 R  διάφορο του μηδενός  αλλά  ο δίσκος  δεν θα περιστραφεί  διότι η στατική τριβή κάνει ροπή μεγαλύτερη της ροπής της τάσης του νήματος  και ο δίσκος θα μείνει ακίνητος

εάν  Ν = 50 Ν  και   μ_s = 0,3  >  0,2 = 1/5    τότε   T_s  =  μ_s N =  0,3  50 Ν = 15 Ν    οπότε  Στ_(Κ) =  T_s R - T_ν R ημ30°  =  ( 15 - 20  ½ ) R  = 5 R  διάφορο του μηδενός αλλά  ο δίσκος  δεν θα περιστραφεί  διότι η στατική τριβή κάνει ροπή μεγαλύτερη της ροπής της τάσης του νήματος  και ο δίσκος θα μείνει ακίνητος

εάν  Ν = 70 Ν  και   μ_s = 0,3  >  0,2 = 1/5    τότε   T_s  =  μ_s N =  0,3  70 Ν = 21 Ν    οπότε  Στ_(Κ) =  T_s R - T_ν R ημ30°  =  ( 21 - 20  ½ ) R  = 11 R  διάφορο του μηδενός  αλλά  ο δίσκος  δεν θα περιστραφεί  διότι η στατική τριβή κάνει ροπή μεγαλύτερη της ροπής της τάσης του νήματος  και ο δίσκος θα μείνει ακίνητος

                  ΘΕΜΑ  A

τη στιγμή t₁ : φ(x) = 3π + πx     φ = 0 => x = - 3 m      x  αυξάνεται  και  φ   αυξάνεται  το κύμα διαδίδεται προς τα αριστερά 

εξίσωση κύματος τη στιγμή t₁ :  y(x , t₁) = 0,3 ημ(3π + πx) = 0,3 ημ(2πt₁/T + πx + θ)      

        2π/λ = π => λ = 2 m           2πt₁/T + θ = 3π    

σε χρόνο Τ το κύμα διανύει απόσταση λ = 2 m   σε χρόνο 2Τ το κύμα διανύει απόσταση 2λ = 4 m  

  φ₁(x)  =  2πt₁/T + πx + θ  = 3π + πx

  φ₂(x)  =  2πt₂/T + πx + θ  =  2π(t₁+2Τ)/T + πx + θ  =  2πt₁/T + 4π + πx + θ  =  3π + πx + 4π =>  φ₂(x) = 7π + πx   

  T = 1 s     t₁ = 2 s        v = λ/T = 2m / 1s = 2 m/s η ταχύτητα διαδόσεως του κύματος

     φ₁  =  2πt₁/T + πx + θ  = 3π + πx  =>   2π2/1 + θ  = 3π  =>  θ = - π   

  άρα  η εξίσωση κύματος είναι :  y(x , t) =  0,3 ημ(2πt/T + πx - π)   

για t = 1s   έχουμε :  y(x , t=1s) =  0,3 ημ(2π1/1 + πx - π)  =  0,3 ημ(π + πx)  =  - 0,3 ημ(πx)     x ³ -1 m   διότι  π + πx ³ 0