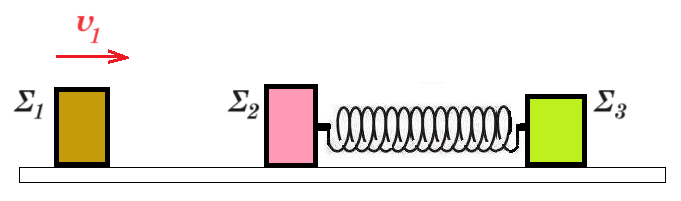
Αρχικά τα σώματα Σ₂ , Σ₃   με μάζες  m₂ = 2kg  m₃ = 4kg  είναι ακίνητα επάνω στο λείο οριζόντιο επίπεδο  δεμένα στα άκρα οριζοντίου ιδανικού ελατηρίου  σταθεράς  k = 4800 N/m  το οποίο είναι στο φυσικό του μήκος.  Σώμα Σ₁ μάζας  m₁ = 1kg  κινούμενο με οριζόντια ταχύτητα  υ₁ = 9 m/s  συγκρούεται κεντρικά ελαστικά με το σώμα Σ₂. 

α)  Βρείτε την μέγιστη συσπείρωση του ελατηρίου.

β)  Βρείτε τον ρυθμό μεταβολής της κινητικής ενέργειας του Σ₃ τη στιγμή που το Σ₂ έχει ταχύτητα  + 4 m/s.

a)    v₁' = v₁ (m₁ - m₂)/(m₁ + m₂) = 9 (1 - 2)/(1 + 2) = - 3 m/s  

        v₂' = 2 v₁ m₁/(m₁ + m₂) = 2 9 1/3 = + 6 m/s 

το Σ₂ μετά την ελαστική κρούση ασκεί δύναμη στο ελατήριο το οποίο συσπειρώνεται  ενώ το Σ₂  δεχόμενο αντίθετη δύναμη από το ελατήριο κινείται προς τα δεξιά επιβραδυνόμενο 

το ελατήριο ασκεί προς τα δεξιά δύναμη στο Σ₃  το οποίο επιταχύνεται  

κάποια στιγμή οι ταχύτητες των Σ₂ Σ₃  θα γίνουν ίσες  έστω  υ₂ = v₃ = v

το σύστημα των Σ₂ Σ₃ ελατηρίου θεωρείται μονωμένο η συνισταμένη των εξωτερικών δυνάμεων ισούται με μηδέν οπότε  διατήρηση ορμής :   m₂ v₂' = m₂ v₂ + m₃ v₃   (1)  =>  m₂ v₂' = m₂ v + m₃ v  => 2 6 = 2 v + 4 v => v = 2 m/s

διατήρηση ενέργειας :  ½ m₂ (v₂')² =  ½ m₂ v₂²  +  ½ m₃ v₃²  +  ½ k x²    (2)   =>

  =>   ½ m₂ (v₂')² =  ½ m₂ v²  +  ½ m₃ v²  +  ½ k x²   =>

  =>  2 6² =  2 2²  +  4 2²  +  4800 x²  => 24 = 2400 x²  => x = 0,1 m   μέγιστη συσπείρωση ελατηρίου

β)     όταν  v₂ = 4 m/s   από (1) =>  m₂ v₂' = m₂ v₂ + m₃ v₃  =>  2 6 = 2 4 + 4 v₃  =>  v₃ = 1 m/s  

από  (2) =>   ½ m₂ (v₂')² =  ½ m₂ v₂²  +  ½ m₃ v₃²  +  ½ k x²  =>  2 6² =  2 4²  +  4 1²  +  4800 x²  => 

  =>  72  -  32  -   4  =  4800 x²  =>   x² = 36 / 4800 = 3 / 400 m²  =>  x = √3 / 20 m 

ρυθμός μεταβολής κινητικής ενέργειας του Σ₃ :  dK₃/dt = m₃ v₃ a₃ = v₃ F_ελατ = v₃ k x = 1 m/s  4800 N/m  √3 / 20 m  =  240√3 J/s