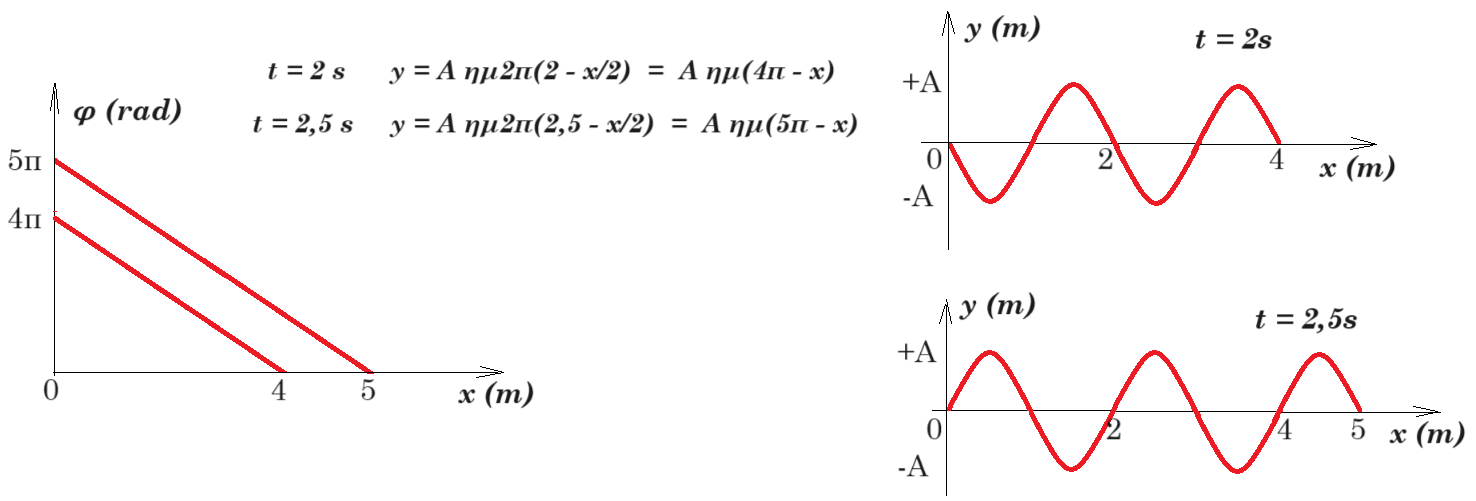2025
ΘΕΜΑ A βασισμένο στο 01/11/2020 ΠΑΡΑΣΥΡΗΣ - ΣΙΑΠΕΡΑ
Α2. Αρχικά ο μαγνήτης σχεδόν εφάπτεται με το άκρο Γ του πηνίου. Ο μαγνήτης απομακρύνεται με σταθερή ταχύτητα υ σε διεύθυνση κατά τον άξονα του πηνίου, σε πολύ μεγάλη απόσταση από το πηνίο. Κατά την διάρκεια της απομάκρυνσης του μαγνήτη από το πηνίο,
α) η τάση που επάγεται στα άκρα του πηνίου είναι αντιστρόφως ανάλογη της ταχύτητας του μαγνήτη
β) στο άκρο Γ του πηνίου εμφανίζεται βόρειος μαγνητικός πόλος
γ) στα άκρα Α και Β εμφανίζεται τάση από επαγωγή με το + στο Α
δ) στα άκρα Α και Β εμφανίζεται τάση από επαγωγή με το + στο Β.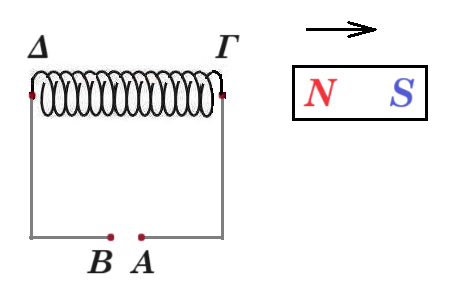
ο μαγνήτης απομακρύνεται με τον βόρειο πόλο, έτσι μειώνεται το πλήθος των μαγνητικών γραμμών που διέρχονται μέσα από το πηνίο
το πηνίο αντιδρά και προσπαθεί να "συγκρατήσει" τον βόρειο πόλο του μαγνήτη που απομακρύνεται έτσι γίνεται το ίδιο μαγνήτης με τον νότιο πόλο στο άκρο του Γ και τον βόρειο πόλο στο άκρο του Δ άρα το πηνίο διαρρέεται από ρεύμα (κίνηση ηλεκτρονίων)
τα ηλεκτρόνια που κινούνται στο εσωτερικό του πηνίου συσσωρεύονται στο σημείο Α διότι το κύκλωμα είναι ανοικτό έτσι το σημείο Α φορτίζεται αρνητικά και το σημείο Β φορτίζεται θετικά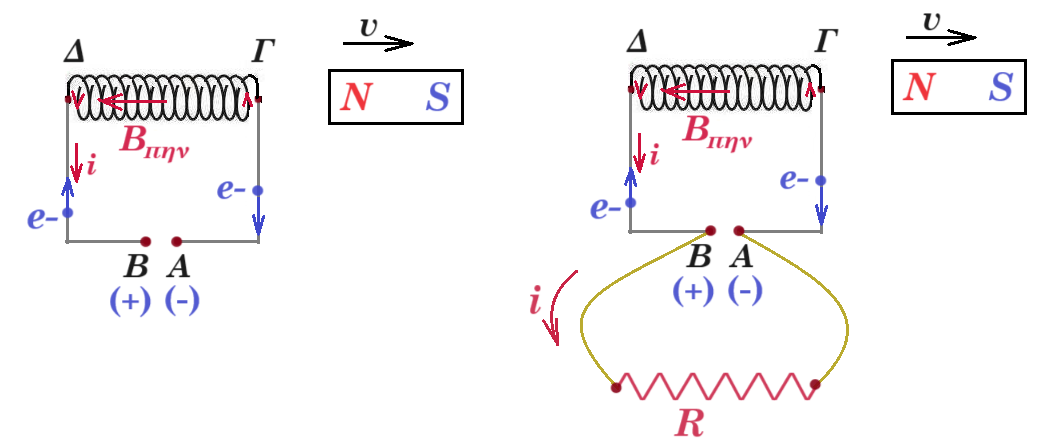
ΘΕΜΑ Δ 2025 παρόμοιo
Ομογενής αγώγιμος δίσκος μάζας Μ = 4kg, ακτίνας R = 9/8π m είναι ακίνητος πάνω σε μια δοκό ΑΒ μήκους (ΑΒ)=4m, μάζας m = 1kg, στο σημείο Ρ όπου (ΑΡ) = 0,5m. Το άνω άκρο της δοκού Α συνδέεται με άρθρωση σε κατακόρυφο τοίχο, ενώ το κάτω άκρο της ακουμπά σε λείο οριζόντιο δάπεδο σχηματίζοντας γωνία θ με αυτό, όπου ημθ=0,6 και συνθ=0,8. Η ισορροπία του δίσκου εξασφαλίζεται από κατακόρυφο νήμα που εφάπτεται στον δίσκο στο σημείο Ε, όπως στο σχήμα. 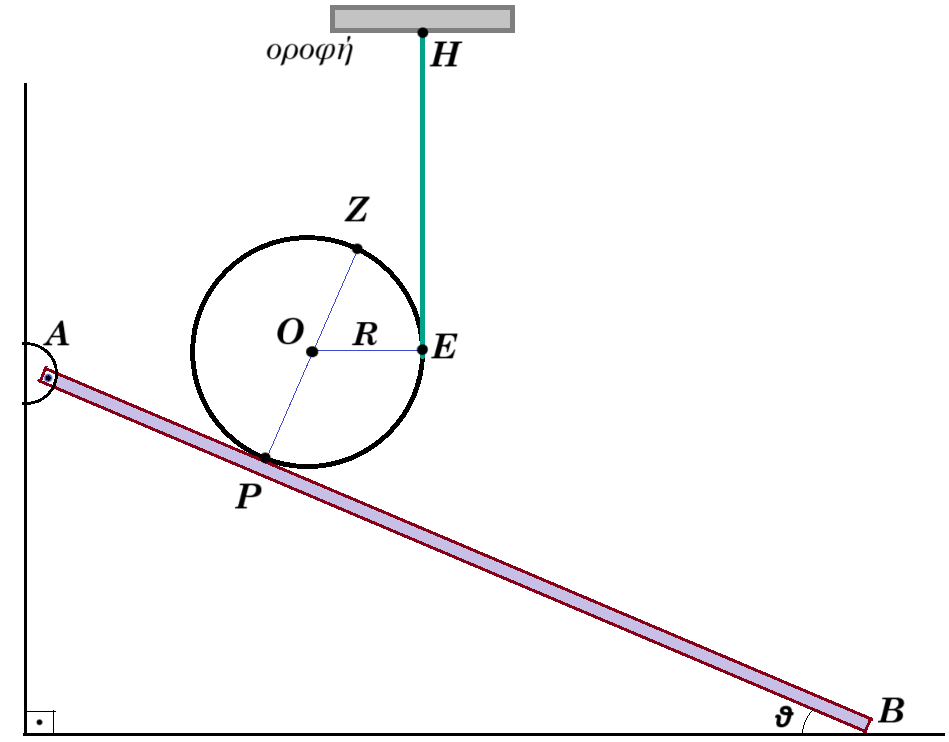
i) Να αποδείξετε ότι ο δίσκος δέχεται κατακόρυφη δύναμη από την δοκό και να υπολογίσετε τις συνιστώσες της, μια κάθετη και μια παράλληλη στην επιφάνεια της δοκού.
ii) Σε μια στιγμή t=0 κόβουμε το νήμα, οπότε ο δίσκος κυλίεται (χωρίς να ολισθαίνει) κατά μήκος της δοκού. Στον χώρο υπάρχει ομογενές μαγνητικό πεδίο Β = 0,01 Τ του οποίου οι δυναμικές γραμμές είναι οριζόντιες προς τον αναγνώστη.
α) Κάποιος συμμαθητής σας υποστηρίζει ότι στη διάρκεια της κίνησης του δίσκου ασκείται τριβή ολίσθησης πάνω του από την σανίδα. Συμφωνείτε ή διαφωνείτε με την άποψη αυτή;
β) Κάποιος άλλος συμμαθητής σας υποστηρίζει αντίθετα, ότι κατά την κύλιση δεν ασκείται τριβή στον δίσκο. Σας βρίσκει σύμφωνο η θέση αυτή ή όχι και γιατί;
iii) Να υπολογιστεί η ταχύτητα του σημείου Ζ της περιφέρειας του δίσκου, τη χρονική στιγμή t1=2s όπου το κέντρο του δίσκου έχει μετατοπισθεί κατά 6 m.
iv) Αφού υπολογίστε τα μέτρα των δυνάμεων που ασκούνται στον δίσκο, στη διάρκεια της κίνησης, να υπολογιστούν τα έργα των δυνάμεων αυτών από 0 έως t1.
v) Υπολογίστε τις δυνάμεις που δέχεται η ράβδος ΑΒ στα άκρα της Α και Β συναρτήσει της μετατόπισης x του κέντρου Ο του δίσκου για 0 £ x £ 3m.
vi) Σχεδιάστε την τάση που εμφανίζεται μεταξύ του κέντρου Ο του δίσκου και οποιοδήποτε σημείου της περιφέρειας του δίσκου συναρτήσει του χρόνου καθώς ο δίσκος κυλίεται πάνω στην δοκό με σταθερή γωνιακή επιτάχυνση και τη χρονική στιγμή t' = 1s η μεταβολή της δυναμικής βαρυτικής ενέργειας του δίσκου είναι - 48 J.
Δίνεται √7 » 2,65 και g=10m/s2.
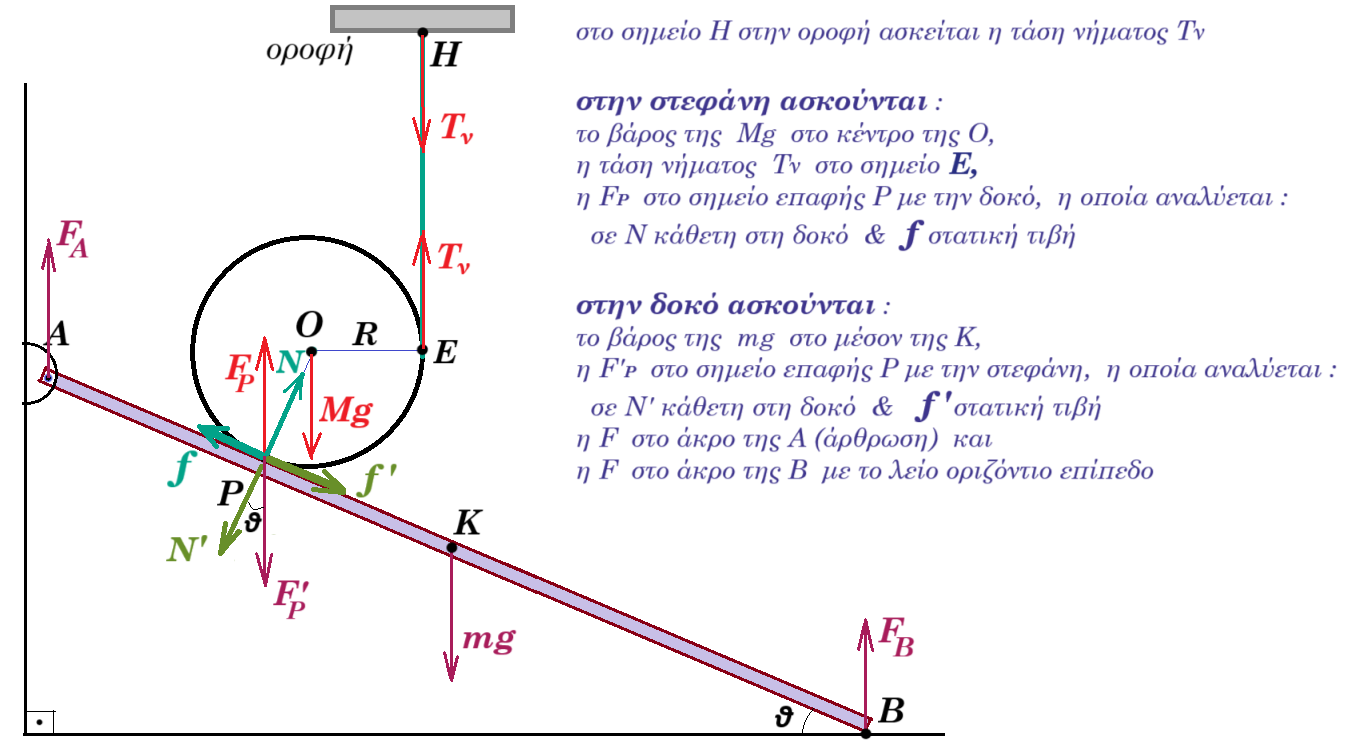
ροπές ως προς Ο : Στ(Ο) = 0 => Τν R = FP R ημθ => Τν = FP ημθ => FP = Τν / 0,6
ΣFy = 0 => Τν + FP = Mg => FP ημθ + FP = Mg => 1,6 FP = 4 10 => FP = 25 N
Ν = FP συνθ = 25 Ν 0,8 => Ν = 20 Ν f = FP ημθ = 25 Ν 0,6 => f = 15 Ν
τη στιγμή t0 = 0 κόβουμε το νήμα οπότε ο δίσκος αρχίζει να κυλίεται πάνω στην δοκό η ταχύτητα του δίσκου vcm αυξάνεται η γωνιακή ταχύτητά του ω αυξάνεται
xcm = 0,5 acm t12 => 6m = 0,5 acm 22 => acm = 3 m/s2
vcm = acm t1 = 3 m/s2 2 s => vcm = 6 m/s vZ = 2 vcm = 12 m/s
αγων = acm / R = 3 m/s2 / 9/8π m => αγων = 8π/3 rad/s2
ω = αγων t1 = 8π/3 rad/s2 2 s = 16π/3 rad/s
vcm = ω R = 16π/3 rad/s 9/8π m => vcm = 6 m/s
ΣF = M acm => Mg ημθ - Τ = M acm => 40 0,6 - Τ = 4 3 => T = 12 N
WT = T xcm συν180° = - 12 Ν 6 m = - 72 J
Ww = Mg ημθ xcm = 40 N 0,6 6 m = 144 J
θ = 0,5 αγων t12 = 0,5 8π/3 rad/s2 4 s2 => θ = 16π/3 rad
N = θ / 2π = 16π/3 rad / 2π => Ν = 8/3 περιστροφές N 2πR = 8/3 2π 9/8π m = 6 m = xcm
ισορροπία ράβδου ΑΒ :
Τ' = Τ = 12 Ν Ν' = Ν = Mg συνθ = 40 0,8 = 32 Ν
ροπές ως προς Α : Στ(Α) = 0 =>
=> FB (AB) συνθ - Ν' (0,5 + x) - mg (AB)/2 συνθ = 0 =>
=> FB 4 0,8 - 32 (0,5 + x) - 10 2 0,8 = 0 => FB 3,2 - 32 (0,5 + x) - 16 = 0 =>
=> FB = 10 (0,5 + x) + 5 => FB(x) = 10 + 10.x 0 £ x £ 3m
ΣFx = 0 => FA,x + T ' συνθ - Ν' ημθ = 0 => FA,x + 12 0,8 - 32 0,6 = 0 =>
=> FA,x = 9,6 Ν δεξιά
ροπές ως προς Β : Στ(Β) = 0 =>
=> - FA,y (AB) συνθ - FA,x (AB) ημθ + Ν' ( 4 - 0,5 - x) + mg (AB)/2 συνθ = 0 =>
=> - FA,y 4 0,8 - 9,6 4 0,6 + 32 (3,5 - x) + 10 2 0,8 = 0 =>
=> - FA,y 3,2 - 23,04 + 32 (3,5 - x) + 16 = 0 =>
=> FA,y = 10 (3,5 - x) + 5 - 7,2 => FA,y(x) = 32,8 - 10.x 0 £ x £ 3m προς τα πάνω
άλλος τρόπος :
ΣFy = 0 => FA,y - T ' ημθ - Ν' συνθ - mg + FB = 0 =>
=> FA,y - 12 0,6 - 32 0,8 - 10 + (10 + 10.x) = 0 =>
=> FA,y - 7,2 - 25,6 - 10 + (10 + 10.x) = 0 => FA,y(x) = 32,8 - 10.x
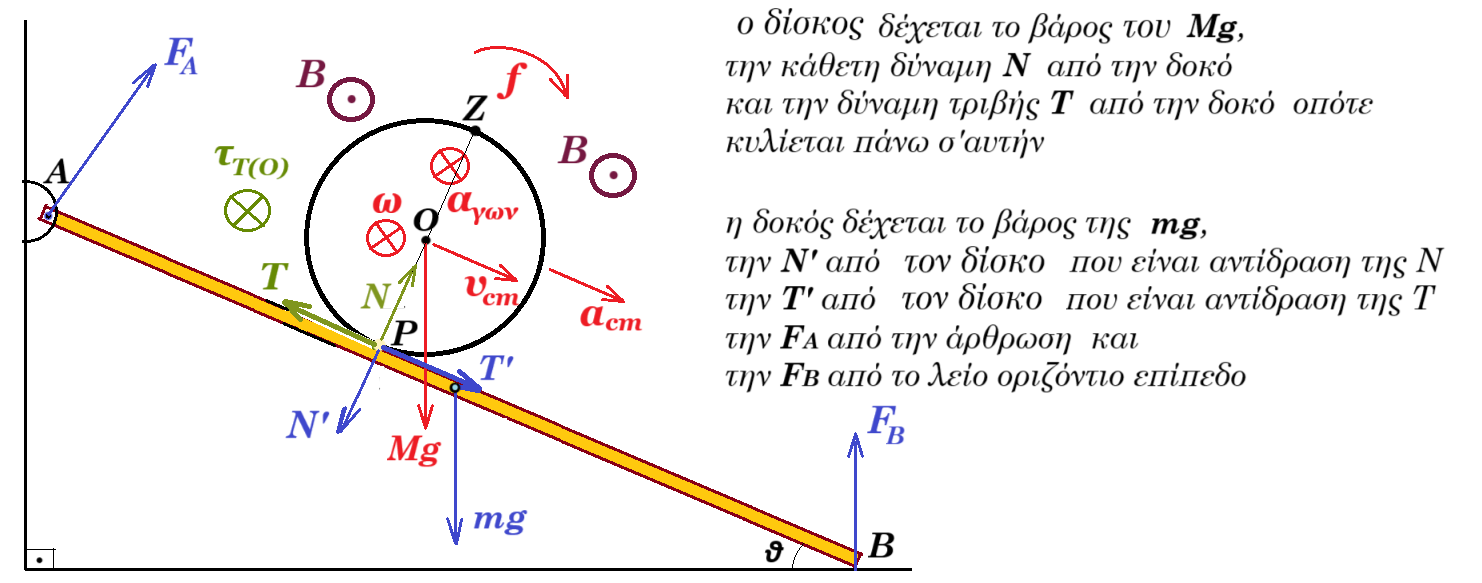
acm = R aγων Στ(Ο) = Ιcm aγων => T R = 0,5 M R2 aγων => T = 0,5 M acm
ΣF = M acm => Mg ημθ - Τ = Μ αcm => Mg ημθ - 0,5 M acm = Μ αcm =>
=> acm = 2g/3⋅ ημθ = 20/3⋅ 0,6 => acm = 4 m/s2
αγων = acm / R = 4 / 9/8π => αγων = 32π/9 rad/s2
h = x ημθ = 2m 0,6 = 1,2m U = m g h = 4kg 10 m/s2 1,2m = 48 J
acm = αγων R = 32π/9 rad/s2 9/8π m => acm = 4 m/s2
xcm = 0,5 acm t2 => 2 m = 0,5 4 m/s2 t2 => t = 1 s
vcm = acm t = 4 m/s2 1 s = 4 m/s ω = αγων t = 32π/9 rad/s2⋅ t = 32π/9⋅ t (rad/s)
ΔU = - 48 J = 0 - 48 J = Uτελ - Uαρχ => Uαρχ = 48 J = m g h = 4kg 10 m/s2 h => h = 48/40 = 1,2 m = xcm ημθ = x 0,6 => xcm = 2 m
xcm = 0,5 acm t2 => 2 m = 0,5 acm 1 s2 => acm = 4 m/s2
acm = αγων R => 4 m/s2 = aγων 9/8π m => aγων = 32π/9 rad/s2
ω = αγων t = 32π/9 rad/s2 . t = 32π/9 . t (rad/s)
ο δίσκος επάνω στη δοκό διανύει διάστημα (ΡΒ) = 4m - 0,5m = 3,5m οπότε xcm = 0,5 acm t2 => 3,5 m = 0,5 4 m/s2 t2 => t2 = 7/4 s2 => t = √7/2 s » 2,65/2 s = 1,325 s
μεταξύ του κέντρου Ο του δίσκου και οποιοδήποτε σημείου της περιφέρειας αυτού αναπτύσσεται επαγωγική τάση Εεπαγ = 0,5 Β ω R2 = 0,5 0,01 T 32π/9 rad/s ⋅ t ( 9/8π m )2 = 0,5 0,01 4 9/8π⋅ t (Volt) =>
=> Εεπαγ = 9/400π⋅ t (Volt) 0 £ t £ 1,325 s
ΘΕΜΑ Δ βασισμένο στο 2006
Η διπλή τροχαλία μάζας Μ»0 με ακτίνες r1 και r2 = 2r1 του σχήματος, μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από το κέντρο της Ο. Τα νήματα (1) και (2) είναι αβαρή - μή εκτατά, η αγώγιμη ράβδος ΚΛ (σώμα Σ1) μάζας m1=4kg, ωμικής αντίστασης R=2Ω, μήκους l=1m, το σώμα Σ2 μάζας m2=1kg είναι κολλημένο με ράβδο ΑΓ (σώμα Σ3) μάζας m3=1kg, μήκους l=1m, το οποίο συγκρατείται από κατακόρυφο ελατήριο σταθεράς k=100Ν/m. Το σύστημα αρχικά ισορροπεί όπως φαίνεται στο σχήμα. Στα άκρα της η οριζόντια ράβδος ΑΓ που φέρει μικρές ακίδες απέχει από την οριζόντια επιφάνεια υγρού απόσταση h=0,2m. 
Κάποια χρονική στιγμή, την οποία θεωρούμε ως χρονική στιγμή μηδέν (t0 = 0), τα σώματα Σ2 και Σ3 αποκολλώνται και το Σ3 εκτελεί απλή αρμονική ταλάντωση κατά τη διεύθυνση της κατακορύφου.
Δ1. Να γραφεί η εξίσωση της μεταβολής της κινητικής ενέργειας του σώματος Σ3 σε συνάρτηση με το χρόνο, να γίνει η γραφική παράστασή της σε βαθμολογημένους άξονες, θεωρώντας ως θετική φορά, τη φορά προς τα επάνω. Επίσης να γραφεί η εξίσωση της δύναμης του ελατηρίου συναρτήσει του χρόνου και συναρτήσει της απομάκρυνσης από τη θέση ισορροπίας του Σ3, να γίνει η γραφική παράστασή σε βαθμολογημένους άξονες Μονάδες 10
Καθώς η ράβδος ΑΓ ταλαντώνεται ακουμπούν οι ακίδες στην επιφάνεια του υγρού στα σημεία Α', Γ' οπότε δημιουργούνται εγκάρσια κύματα πλάτους Α0 που έχουν ταχύτητα διαδόσεως υδ = 2/π m/s. Θεωρούμε σημείο Ρ της επιφάνειας του υγρού το οποίο απέχει 0,9m και 0,8m αντίστοιχα από τα σημεία Α' και Γ' που είναι οι προβολές των Α και Γ.
Δ2. Να γραφεί η εξίσωση της απομάκρυνσης του σημείου Ρ σε συνάρτηση με το χρόνο. Μονάδες 4
Δ3. Βρείτε πόσα σημεία της ευθείας Α'Γ' ταλαντώνονται με μέγιστο πλάτος. Μονάδες 4
Δ4. Αν η τροχαλία στρέφεται με γωνιακή επιτάχυνση μετά την αποκόλληση των σωμάτων Σ2 και Σ3, μελετήστε την κίνηση της ράβδου ΚΛ μέσα στο οριζόντιο ομογενές μαγνητικό πεδίο εντάσεως Β = 0,1 Τ. Ποία η ένδειξη του βολτομέτρου; Μονάδες 7
Η τριβή ανάμεσα στην τροχαλία και στα νήματα είναι αρκετά μεγάλη, ώστε να μην παρατηρείται ολίσθηση, g=10m/s2, η ωμική αντίσταση του βολτομέτρου : RV = 98 Ω.
Δ1. ισορροπία Σ1 : Τ1 = m1 g = 40 N Στ(Ο) = 0 => T1 r1 = T2 r2 => 40 r1 = Τ2 2r1 => T2 = 20 N
ισορροπία Σ2,3 : Τ2 = m2,3 g + Fελατ => Τ2 = m2,3 g + k Δl2,3 => 20 = 20 + 100 Δl => Δl2,3 = 0 το ελατήριο έχει το φυσικό του μήκος
ισορροπία Σ3 όταν είναι μόνο του : m3 g = k Δl3 => 10 = 100 Δl3 => Δl3 = 0,1 m συσπείρωση ελατηρίου
το πλάτος ταλάντωσης του Σ3 θα είναι : Α = Δl3 = 0,1 m διότι αρχικά είναι ακίνητο 0,1 m υψηλότερα από τη Θ.Ι. του
κυκλική συχνότητα ταλάντωσης Σ3 : ω2 = k / m3 = 100 / 1 => ω = 10 rad/s f = ω / 2π = 10 / 2π = 5/π Hz
x(t) = 0,1 ημ(10t + π/2) v(t) = 1 συν(10t + π/2) a(t) = - 10 ημ(10t + π/2)
Κ = ½ m3 v2 = ½ 1 1 συν2(10t + π/2) = 0,5 συν2(10t + π/2) = 0,5 { 1 + συν(20t + π) } / 2 = 0,25 + 0,25 συν(20t + π) = 0,25 - 0,25 συν(20t)
dK/dt = m3 v a = 1 1 συν(10t + π/2) { - 10 ημ(10t + π/2) } = - 10 ημ(10t + π/2) συν(10t + π/2) = - 5 ημ(20t + π) = +5ημ(20t)
ΣF = m3 a => Fελατ - m3 g = m3 a => Fελατ - 10 = 1 { - 10 ημ(10t + π/2) } => Fελατ(t) = 10 - 10 ημ(10t + π/2)
Fελατ(x) = 10 - 100⋅x = - 100⋅(x - 0,1) - 0,1 m £ x £ + 0,1 m
Fελατ(-0,1) = 20 Ν x = - 0,1 m σημαίνει ότι το ελατήριο είναι συσπειρωμένο κατά 0,2 m
Fελατ(0) = 10 Ν x = 0 σημαίνει ότι το ελατήριο είναι συσπειρωμένο κατά 0,1 m
Fελατ(+0,1) = 0 x = + 0,1 m σημαίνει ότι το ελατήριο είναι στο φυσικό του μήκος
Δ2. εγκάρσιο κύμα στην επιφάνεια του υγρού : υδ = λ f => λ = υδ / f = (2/π) / (5/π) = 0,4 m
y1 = A0 ημ(10t - 2πx1/λ) = A0 ημ(10t - 2π 0,9/0,4) = A0 ημ(10t - 4,5π)
y2 = A0 ημ(10t - 2πx2/λ) = A0 ημ(10t - 2π 0,8/0,4) = A0 ημ(10t - 4π)
yP = 2A0 συν(10t - 4,5π - 10t + 4π)/2 ημ(10t - 4,5π + 10t - 4π)/2 = 2A0 συν(π/4) ημ(20t - 8,5π)/2 =
= 2A0 √2/2 ημ(10t - 17π/4) => yP(t) = √2A0 ημ(10t - 17π/4)
Δ3. μέγιστο πλάτος : x1 - x2 = Nλ x1 + x2 = 1m 2x1 = Nλ + 1m => x1 = Nλ / 2 + 0,5m = N 0,2m + 0,5m
0 < x1 < 1m => 0 < N 0,2m + 0,5m < 1m => - 0,5m < N 0,2m < 0,5m => - 5/2 < N < 5/2 => N = -2,-1,0,1,2
N = -2 x1 = (-2) 0,2m + 0,5m = 0,1m
N = -1 x1 = (-1) 0,2m + 0,5m = 0,3m
N = 0 x1 = 0,5m
N = +1 x1 = +1 0,2m + 0,5m = 0,7m
N = +2 x1 = +2 0,2m + 0,5m = 0,9m
Δ4. η τροχαλία στρέφεται με γωνιακή επιτάχυνση αγων
a1 = αγων r1 = αγων r2/2 = a2 / 2 a2 = 2a1
η ράβδος κατέρχεται μέσα στο μαγνητικό πεδίο τα ηλεκτρόνιά της δέχονται δύναμη Lorentz και οδεύουν προς το άκρο Κ το οποίο φορτίζεται αρνητικά ενώ το άκρο Λ φορτίζεται θετικά, έτσι αναπτύσσεται επαγωγική τάση στα άκρα Κ, Λ Εεπαγ = Βlv, το κύκλωμα διαρρέεται από ρεύμα i = Blv / (R+RV) η ράβδος δέχεται δύναμη Laplace FL = Bli = B2l2v/(R+RV) κατακόρυφη προς τα πάνω οπότε ΣF = m1 a1 => m1 g - T1 - FL = m1 a1 => m1 g - T1 - B2l2v/(R+RV) = m1 a1 (1)
Στ(Ο) = Ι(Ο) αγων => T1 r1 - T2 r2 = 0 => T1 r1 - T2 2r1 = 0 => T1 - 2T2 = 0 (2)
το Σ2 ανέρχεται : Τ2 - m2 g = m2 α2 = m2 αγων r2 (3)
(1) + (2) + 2*(3) => m1 g - T1 - B2l2v/(R+RV) + T1 - 2T2 + 2Τ2 - 2m2 g = m1 a1 + 2m2 α2 =>
=> m1 g - B2l2v/(R+RV) - 2m2 g = m1 a1 + 2m2 α2 => a2 = 2a1
=> m1 g - B2l2v/(R+RV) - 2m2 g = m1 a1 + 2m2 2α1 =>
=> (m1 - 2m2) g - B2l2v/(R+RV) = (m1 + 4m2) α1 =>
=> 40 - 20 - 0,01v/100 = 8 α1 => 20 - v 10-4 = 8 a1
-10-4 (v - 200.000) = 8 dv/dt => dv / (v - 200.000) = -1/80.000 dt => ln [ (v - 200.000)/(- 200.000) ] = e - t/80.000 =>
v - 200.000 = - 200.000 e - t/80.000 => v(t) = 200.000 ( 1 - e - t/80.000 )
a(t) = 200.000 / 80.000 e - t/80.000 = 2,5 e - t/80.000
αρχικά η ταχύτητα είναι μηδενική οπότε η αρχική επιτάχυνση της ράβδου ΚΛ είναι : α1 = 20/8 = 2,5 m/s2 = g/4 ενώ το σώμα Σ2 έχει α2 = 2 α1 = 5 m/s2 = g/2
η ταχύτητα αυξάνεται η επιτάχυνση μειώνεται, όταν α1 = 0 => v = 200.000 m/s οριακή ταχύτητα
B2l2/(R+RV)(m1 + 4m2) = 0,01 1 / 800 = 1/80.000 τ = 80.000 s = 22,222 ώρες περίπου 1 μέρα
η ράβδος ΚΛ θα έχει την οριακή ταχύτητα σε χρόνο 5τ = 5 * 22,222 ώρες περίπου 4,5 μέρες
και θα έχει διανύσει x(t) = 200000 t + 16 109 [ e - t / 80000 - 1 ]
ένδειξη βολτομέτρου : V = Εεπαγ - i R = Blv - Blv/(R+RV) R = Blv RV/(R+RV) = 0,1 1 v 98/100 = 0,098 v
x(t) = 200.000 t + 16 109 [ e - t / 80000 - 1 ] v(t) = 200.000 ( 1 - e - t / 80.000 ) a(t) = 2,5 e - t / 80.000
t = 1 s
x = 200.000 1 + 16 109 [ e - 1 / 80000 - 1 ] = 200.000 + 16 109 [ 0,9999875 - 1 ] = 200.000 - 16 109 1,25 10-5 = 200.000 - 199.998,75 = 1,25 m
v = 200.000 ( 1 - e - 1 / 80.000 ) = 200.000 ( 1 - 0,9999875 ) = 2,499984375 m/s = 2,5 m/s
a = 2,5 e - 1 / 80.000 = 2,5 0,9999875 = 2,49996875 m/s2 = 2,5 m/s2
t = 2 s
x = 200.000 2 + 16 109 [ e - 2 / 80000 - 1 ] = 400.000 + 16 109 [ 0,999975 - 1 ] = 400.000 - 16 109 2,5 10-5 = 400.000 - 399.995 = 5 m
v = 200.000 ( 1 - e - 2 / 80.000 ) = 200.000 ( 1 - 0,999975 ) = 4,9999375 m/s = 5 m/s
a = 2,5 e - 2 / 80.000 = 2,5 0,999975 = 2,4999375 m/s2 = 2,5 m/s2
t = 3 s
x = 200.000 3 + 16 109 [ e - 3 / 80000 - 1 ] = 600.000 + 16 109 [ 0,9999625 - 1 ] = 400.000 - 16 109 3,75 10-5 = 600.000 - 599.988,75 = 11,25 m
v = 200.000 ( 1 - e - 3 / 80.000 ) = 200.000 ( 1 - 0,9999625 ) = 7, 499859 m/s = 7,5 m/s
a = 2,5 e - 3 / 80.000 = 2,5 0,9999625 = 2,49990625 m/s2 = 2,5 m/s2
t = 4 s
x = 200.000 4 + 16 109 [ e - 4 / 80000 - 1 ] = 800.000 + 16 109 [ 0,99995000125 - 1 ] = 800.000 - 16 109 0,00004999875 = 800.000 - 799.980 = 20 m
v = 200.000 ( 1 - e - 4 / 80.000 ) = 200.000 ( 1 - 0,99995000125 ) = 9,99975 m/s = 10 m/s
a = 2,5 e - 4 / 80.000 = 2,5 0,99995000125 = 2,499875 m/s2 = 2,5 m/s2
t = 5 s
x = 200.000 5 + 16 109 [ e - 5 / 80000 - 1 ] = 1.000.000 + 16 109 [ 0,9999375 - 1 ] = 1.000.000 - 16 109 6,25 10-5 = 1.000.000 - 999.968,75 = 31,25 m
v = 200.000 ( 1 - e - 5 / 80.000 ) = 200.000 ( 1 - 0,9999375 ) = 12,4996 m/s = 12,5 m/s
a = 2,5 e - 5 / 80.000 = 2,5 0,9999375 = 2,499843755 m/s2 = 2,5 m/s2
μαθηματικά
(m1 - 2m2) g - B2l2v/(R+RV) = (m1 + 4m2) α1 =>
- B2l2/(R+RV) [ v - (m1 - 2m2)g(R+RV) / B2l2 ] = (m1 + 4m2) dv/dt =>
dv / [ v - (m1 - 2m2)g(R+RV) / B2l2 ] = - B2l2/(R+RV)(m1 + 4m2) dt =>
ln { [ v - (m1 - 2m2)g(R+RV)/(B2l2) ] / [ 0 - (m1 - 2m2)g(R+RV) / B2l2 ] } = - B2l2/(R+RV)(m1 + 4m2) t =>
v(t) = (m1 - 2m2)g(R+RV)/(B2l2) [ 1 - exp {- B2l2/(R+RV)(m1 + 4m2) t} ]
v(0) = 0 v( ¥ ) = (m1 - 2m2)g(R+RV)/(B2l2)
a(t) = (m1 - 2m2)g(R+RV) / B2l2 B2l2/(R+RV)(m1 + 4m2) exp {- B2l2/(R+RV)(m1 + 4m2) t} =
= g (m1 - 2m2)/(m1 + 4m2) exp {- B2l2/(R+RV)(m1 + 4m2) t}
a(0) = g (m1 - 2m2)/(m1 + 4m2) a( ¥ ) = 0
dx = v dt = (m1 - 2m2)g(R+RV)/(B2l2) [ 1 - exp {- B2l2/(R+RV)(m1 + 4m2) t} ] dt =>
x(t) = (m1 - 2m2)g(R+RV)/(B2l2) t + (m1 + 4m2)(m1 - 2m2)g(R+RV)2/(B4l4) [ exp {- B2l2/(R+RV)(m1 + 4m2) t} - 1 ]
x(t) = 200000 t + 16 109 [ e - t / 80000 - 1 ]
2004
ΘΕΜΑ 2ο
Για τις παρακάτω ερωτήσεις να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
1. Μια μικρή σφαίρα μάζας m1 συγκρούεται μετωπικά και ελαστικά με ακίνητη μικρή σφαίρα μάζας m2. Μετά την κρούση οι σφαίρες κινούνται με αντίθετες ταχύτητες. Ο λόγος των μαζών m1/m2 των δύο σφαιρών είναι:
α) 1 β) 1/2 γ) 1/3
v1' = - v2' => v1 (m1 - m2)/(m1 + m2) = - 2 m1 v1 /(m1 + m2) => m1 - m2 = - 2 m1 => 3 m1 = m2 => m1/m2 = 1/3 (γ)
4. ∆ύο σώματα Σ1 και Σ2 με ίσες μάζες ισορροπούν κρεμασμένα από κατακόρυφα ιδανικά ελατήρια με σταθερές k1 και k2
αντίστοιχα, που συνδέονται με τη σχέση k1= k2/2.
Απομακρύνουμε τα σώματα Σ1 και Σ2 από τη θέση ισορροπίας τους κατακόρυφα προς τα κάτω κατά x και 2x αντίστοιχα και τα αφήνουμε ελεύθερα την ίδια χρονική στιγμή, οπότε εκτελούν απλή αρμονική ταλάντωση. Τα σώματα διέρχονται για πρώτη φορά από τη θέση ισορροπίας τους:
α. ταυτόχρονα.
β. σε διαφορετικές χρονικές στιγμές με πρώτο το Σ1 .
γ. σε διαφορετικές χρονικές στιγμές με πρώτο το Σ2 .
k1 = m ω12 = m 4π2/Τ12 k2 = m ω22 = m 4π2/Τ22
k1= k2/2 => 2 k1 = k2 => 2 m 4π2/Τ12 = m 4π2/Τ22 => 2 T22 = T12 T1 > T2 (γ)
ΘΕΜΑ 3ο
Ένα τεντωμένο οριζόντιο σχοινί ΟΑ μήκους L εκτείνεται κατά τη διεύθυνση του άξονα x. Το άκρο του Α είναι στερεωμένο ακλόνητα στη θέση x=L, ενώ το άκρο Ο που βρίσκεται στη θέση x=0 είναι ελεύθερο, έτσι ώστε με κατάλληλη διαδικασία να δημιουργείται στάσιμο κύμα με 5 συνολικά κοιλίες. Στη θέση x=0 εμφανίζεται κοιλία και το σημείο του μέσου στη θέση αυτή εκτελεί απλή αρμονική ταλάντωση. Τη χρονική στιγμή t=0 το σημείο x=0 βρίσκεται στη θέση μηδενικής απομάκρυνσης κινούμενο κατά τη θετική φορά. Η απόσταση των ακραίων θέσεων της ταλάντωσης
αυτού του σημείου του μέσου είναι 0,1 m. Το συγκεκριμένο σημείο διέρχεται από τη θέση ισορροπίας του 10 φορές κάθε δευτερόλεπτο και απέχει κατά τον άξονα x απόσταση 0,1 m από τον πλησιέστερο δεσμό.
α. Να υπολογίσετε την περίοδο του κύματος. Μονάδες 6
β. Να υπολογίσετε το μήκος L. Μονάδες 6
γ. Να γράψετε την εξίσωση του στάσιμου κύματος. Μονάδες 6
δ. Να υπολογίσετε το μέτρο της ταχύτητας της ταλάντωσης του σημείου του μέσου x=0 κατά τη χρονική στιγμή που η
απομάκρυνσή του από τη θέση ισορροπίας έχει τιμή y = +0,03 m. Μονάδες 7
κ δ κ δ κ δ κ δ κ δ
4Α = 0,1 m => 2Α = 0,05 m f = 5 Hz T = 0,2 s λ/4 = 0,1 m => λ = 0,4 m
L = 9 0,1 m = 0,9 m
y = 0,05⋅ συν(2πx / 0,4) ⋅ ημ(2π 5 t) = 0,05⋅ συν(5πx) ⋅ ημ(10πt)
0,03 = 0,05⋅ συν(5π 0) ⋅ ημ(10πt) => ημ(10πt) = 0,6 συν(10πt) = ± 0,8
v = 0,05⋅ 10π συν(5πx) ⋅ συν(10πt) = π/2 συν(5πx) ⋅ συν(10πt)
v = π/2⋅ συν(5π 0) ⋅ συν(10πt) = π/2⋅ 1 ⋅ (± 0,8) = ± 0,4π m/s
ΘΕΜΑ 4ο τροποποίηση
Συμπαγής και ομογενής σφαίρα μάζας m=10 kg και ακτίνας R=0,1 m κυλίεται ευθύγραμμα χωρίς ολίσθηση ανερχόμενη κατά μήκος κεκλιμένου επιπέδου γωνίας φ με ημφ=0,56. Τη χρονική στιγμή t=0 το κέντρο μάζας της σφαίρας έχει ταχύτητα με μέτρο υ0=8m/s. Να υπολογίσετε για τη σφαίρα:
α. το μέτρο της γωνιακής ταχύτητας περιστροφής της τη χρονική στιγμή t=0. Μονάδες 6
β. αν το μέτρο του ρυθμού μεταβολής της στροφορμής κατά τη διάρκεια της κίνησής της είναι 1,6 Ν⋅m, δηλαδή η συνισταμένη ροπή ως προς το κέντρο μάζας Ο της σφαίρας, να υπολογίσετε την επιτάχυνση του κέντρου μάζας Ο της σφαίρας και την γωνιακή επιτάχυνσή της. Μονάδες 10
γ. το μέτρο της ταχύτητας του κέντρου μάζας της καθώς ανεβαίνει, τη στιγμή που έχει διαγράψει 30/π περιστροφές. Μονάδες 9
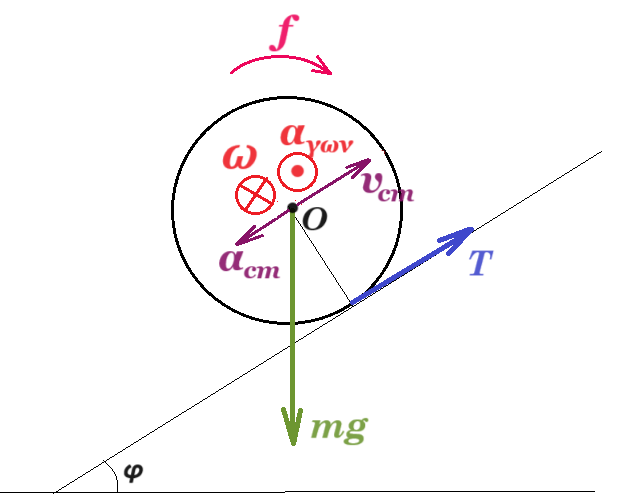
α) vcm = v0 = ω0⋅R => 8 m/s = ω0 ⋅ 0,1 m => ω0 = 80 rad/s
β) dL/dt = Στ(Ο) = Τ⋅R => 1,6 Ν⋅m = Τ⋅ 0,1 m => Τ = 16 Ν
ΣF = m acm => T - mg ημφ = m acm => 16 - 10 10 0,56 = 10 acm => 16 - 56 = 10 acm => acm = - 4 m/s2
αγων = acm / R = - 4 m/s2 / 0,1 m => αγων = - 40 rad/s2
γ) N = 30/π στροφές => θ = Ν 2π = 30/π 2π = 60 rad
θ = ω0 t + ½ αγων t2 => 60 = 80 t - ½ 40 t2 => t2 - 4 t + 3 = 0 => (t - 3) (t - 1) = 0 => t = 1 s ή t = 3 s
t = 1 s ω = ω0 + αγων t = 80 - 40 = 40 rad/s vcm = ω⋅R = 40 0,1 = +4 m/s η σφαίρα ανέρχεται στο κεκλιμένο
t = 3 s ω = ω0 + αγων t = 80 - 40⋅3 = - 40 rad/s vcm = ω⋅R = - 40 0,1 = - 4 m/s η σφαίρα κατέρχεται στο κεκλιμένο
2005
ΘΕΜΑ 3ο
Κατά μήκος του άξονα x'x εκτείνεται ελαστική χορδή. Στη χορδή διαδίδεται εγκάρσιο αρμονικό κύμα. Η εγκάρσια
απομάκρυνση ενός σημείου Π1 της χορδής περιγράφεται από την εξίσωση: y1 = A ημ(30πt) (SI)
ενώ η εγκάρσια απομάκρυνση ενός σημείου Π2, που βρίσκεται 6 cm δεξιά του σημείου Π1, περιγράφεται από την
εξίσωση: y2 = A ημ(30πt + π/6) (SI)
Η απόσταση μεταξύ των σημείων Π1 και Π2 είναι μικρότερη από ένα μήκος κύματος.
α. Ποια είναι η φορά διάδοσης του κύματος; Μονάδες 3
β. Ποια είναι η ταχύτητα διάδοσης του κύματος; Μονάδες 6
γ. Αν η ταχύτητα διάδοσης του κύματος είναι ίση με την μέγιστη ταχύτητα ταλάντωσης των σημείων της χορδής,
να υπολογίσετε το πλάτος του κύματος. Μονάδες 5
δ. Στο σχήμα που ακολουθεί, απεικονίζεται ένα στιγμιότυπο του κύματος.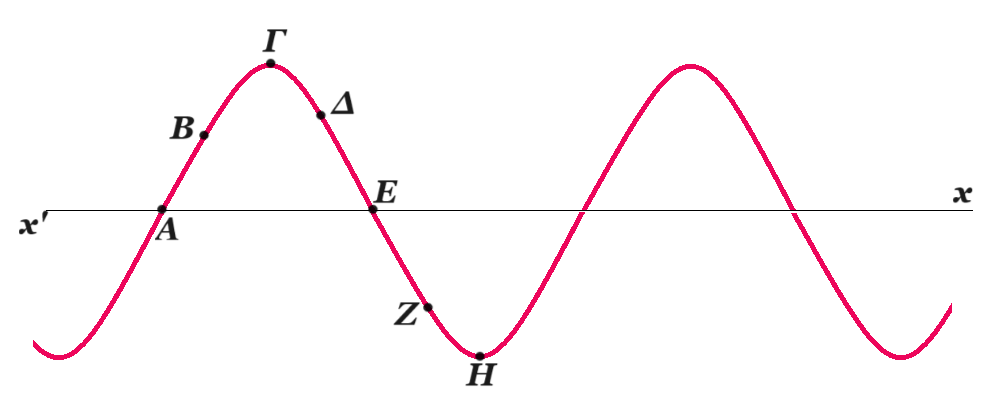
Εκείνη τη στιγμή σε ποια από τα σημεία Α, Β, Γ, ∆, Ε, Ζ και Η η ταχύτητα ταλάντωσης είναι μηδενική και σε ποια είναι μέγιστη (κατ’ απόλυτη τιμή); Ποια είναι η φορά της ταχύτητας ταλάντωσης των σημείων Β, ∆ και Ζ; Μονάδες 7
ε. Να γράψετε την εξίσωση του κύματος που όταν συμβάλλει με το προηγούμενο, δημιουργεί στάσιμο κύμα.
α) ω = 30π rad/s => f = 15 Hz T = 1/15 s 2πx/λ = 2π 6cm/λ = π/6 => λ = 72 cm
η φάση του Π2 είναι μεγαλύτερη από τη φάση του Π1 το κύμα οδεύει προς τα αριστερά
β) v = λ f = 0,72 m 15 Hz = 10,8 m/s
γ) y1 = A ημ(30πt) υ1 = A 30π συν(30πt) 10,8 = Α 30π => Α = 0,36/π m
δ) μηδενική ταχύτητα έχουν τα σημεία Γ και Η μεγιστη ταχύτητα έχουν τα Α (θετική και Ε (αρνητική)
το Β θετική (προς τα πάνω) το Δ αρνητική (προς τα κάτω) το Ζ αρνητική (προς τα κάτω)
ε) y = 0,36/π ημ(30πt - 2πx/0,72)
2006
ΘΕΜΑ 4ο
Άκαμπτη ομογενής ράβδος ΑΓ με μήκος l και μάζα Μ=3kg έχει το άκρο της Α αρθρωμένο και ισορροπεί οριζόντια. Στο άλλο άκρο Γ ασκείται σταθερή κατακόρυφη δύναμη F μέτρου 9Ν, με φορά προς τα κάτω. Η ράβδος ΑΓ εφάπτεται στο σημείο Β με στερεό που αποτελείται από δύο ομοαξονικούς κυλίνδρους με ακτίνες R1=0,1m και R2=0,2m, αμελητέας μάζας, όπως φαίνεται στο σχήμα.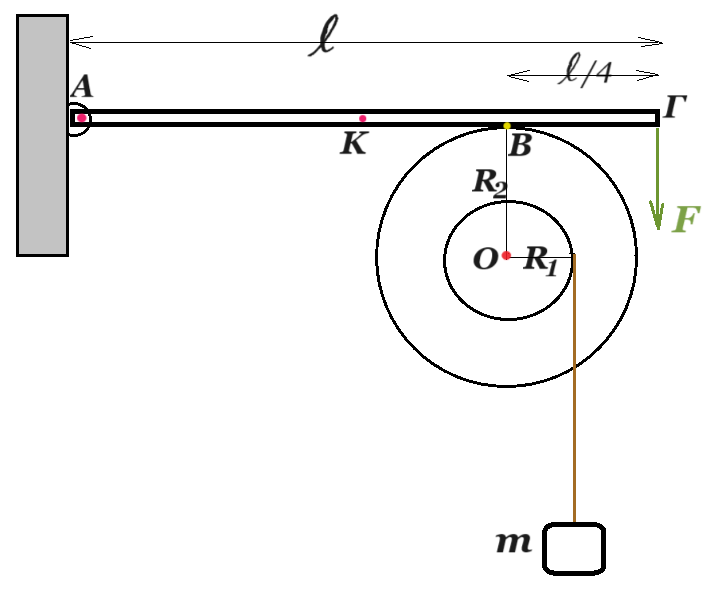
Η απόσταση του σημείου επαφής Β από το άκρο Γ της ράβδου είναι l/4. To στερεό μπορεί να περιστρέφεται χωρίς τριβές, σαν ένα σώμα γύρω από σταθερό οριζόντιο άξονα που περνάει από το κέντρο του Ο. Ο άξονας περιστροφής συμπίπτει με τον άξονα συμμετρίας των δύο κυλίνδρων. Γύρω από τον κύλινδρο ακτίνας R1 είναι τυλιγμένο αβαρές και μη εκτατό νήμα στο άκρο του οποίου κρέμεται σώμα μάζας m=1kg.
α. Να υπολογίσετε την κατακόρυφη δύναμη που δέχεται η ράβδος στο σημείο Β από το στερεό. Μονάδες 5
β. Αν το σώμα μάζας m ισορροπεί, να βρείτε το μέτρο της δύναμης της στατικής τριβής μεταξύ της ράβδου και του στερεού. Μονάδες 5
γ. Υπολογίστε την δύναμη που δέχεται η ράβδος στο άκρο της Α. Μονάδες 5
Στο σημείο επαφής Β μεταξύ ράβδου και στερεού ρίχνουμε ελάχιστη ποσότητα λιπαντικής ουσίας έτσι, ώστε να μηδενιστεί η τριβή.
δ. Να υπολογίσετε το μέτρο της ταχύτητας του σώματος μάζας m, όταν θα έχει ξετυλιχθεί νήμα μήκους 0,5m. Να θεωρήσετε ότι το νήμα ξετυλίγεται χωρίς να ολισθαίνει στον εσωτερικό κύλινδρο. Το στερεό περιστρέφεται με γωνιακή επιτάχυνση αγων = 10 rad/s2. Βρείτε την ροπή που δέχεται το στερεό ως προς τον άξονα περιστροφής του καθώς το σώμα κατέρχεται. Μονάδες 5
ε. Στοιχειώδης μάζα Δm του στερεού που απέχει απόσταση r από τον άξονα περιστροφής, έχει κινητική ενέργεια 10-5 J και στροφορμή 10-6 kg⋅ m2/s ως προς τον άξονα περιστροφής του στερεού. Bρείτε την στροφορμή του σώματος μάζας m ως προς τον άξονα περιστροφής του στερεού, καθώς και τον ρυθμό μεταβολής της κινητικής ενέργειάς του, όταν αυτό κατέρχεται 1m. Μονάδες 5
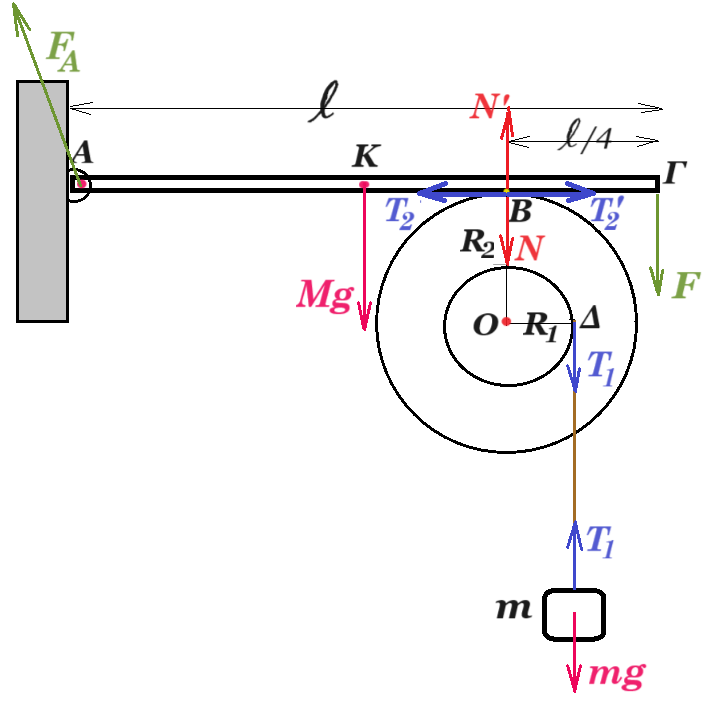
α) ισορροπία σώματος : Τ1 = mg = 10 N
το στερεό δέχεται δυνάμεις : Τ1 στο σημείο Δ, Ν και Τ2 τριβή από τη ράβδο ΑΓ στο σημείο Β,
Στ(Ο) = 0 => Τ2 R2 - T1 R1 = 0 => T2 2R1 = T1 R1 => T2 = T1 /2 = 5 N
β) η ράβδος ΑΓ δέχεται δυνάμεις το βάρος Mg, τις Τ2' = - Τ2 και Ν' = - Ν από το στερεό, την F στο άκρο της Γ και την FΑ στο άκρο της Α
Στ(A) = 0 => N' 3l/4 - Mg l/2 - F l = 0 => N' 3/4 - 30/2 - 9 = 0 => N' = 32 N
γ) FA,x = - T2' = - 5 N προς τα αριστερά
FA,y + N' - F - Mg = 0 => FA,y + 32 - 9 - 30 = 0 => FA,y = 7 N προς τα πάνω
FA2 = FA,x2 + FA,y2 = 52 + 72 = 25 + 49 = 74 => FA = √74 N
δ) το σώμα κατέρχεται επιταχυνόμενο : mg - T1 = m a => 10 - T1 = a (1)
το στερεό περιστρέφεται με γωνιακή επιτάχυνση αγων = α / R1 => α = αγων R1 = 10 rad/s2 0,1 m = 1 m/s2 (2)
0,5 m = 0,5 1 m/s2 t2 => t = 1 s v = a t = 1 m/s2 1 s = 1 m/s
(1) => T1 = 9 N τ(Ο) = Τ1 R1 = 9 N 0,1 m = 0,9 N⋅m
ε) K = ½ Δm v2 = ½ Δm ω2 r2 L = Δm v r = Δm ω r2
Κ / L = ω/2 => 10-5 / 10-6 = ω/2 => ω = 20 rad/s
ω = αγων t = a/R1⋅ t => 20 rad/s = a / 0,1m ⋅ t => a ⋅ t = 2
h = ½ a t2 => h = ½ a ⋅ t t => 1 = ½ 2 t => t = 1 s
οπότε α = 2 m/s2 αγων = ω / t = 20 rad/s / 1 s = 20 rad/s2 v = a t = 2 m/s2 1 s => v = 2 m/s
στροφορμή σώματος : L = m v R1 = m ω R12 = 1 kg 20 rad/s 0,01 m2 = 0,2 kg m2/s
ρυθμός μεταβολής κινητικής ενέργειας σώματος : dK/dt = m v a = 1 kg 2 m/s 2 m/s2 = 4 J/s
.............................................................................................................................................................................................
2007
ΘΕΜΑ 3ο
Σε μια χορδή δημιουργείται στάσιμο κύμα, η εξίσωση του οποίου είναι y = 10 συν(πx/4) ⋅ ημ(20πt), όπου x, y δίνονται σε cm και t σε s. Να βρείτε:
α. τις εξισώσεις των δύο κυμάτων που παράγουν το στάσιμο κύμα. Μονάδες 9
β. την ταχύτητα που έχει τη χρονική στιγμή t=0,1 s ένα σημείο της χορδής το οποίο απέχει 3 cm από το σημείο x=0. Μονάδες 8
γ. σε ποιες θέσεις υπάρχουν κοιλίες μεταξύ των σημείων xΑ=3 cm και xB=9 cm. Μονάδες 8
α) y = 10 συν(πx/4) ⋅ ημ(20πt) = 2A συν(2πx/λ) ⋅ ημ(2πft)
2A = 10 cm => A = 5 cm π/4 = 2π/λ => λ = 8 cm 20π = 2πf => f = 10 Hz
y1 = 5 ημ(20πt - πx/4) y2 = 5 ημ(20πt + πx/4)
β) y = 10 συν(πx/4) ⋅ ημ(20πt) = 10 συν(3π/4) ⋅ ημ(20π 0,1) = 10 (- √2/2) ⋅ ημ(2π) = 0
v = 10⋅ 20π συν(πx/4) ⋅ συν(20πt) = 200π συν(3π/4) ⋅ συν(20π 0,1) = 200π (- √2/2) ⋅ συν(2π) =>
=> v = - 100π √2 cm/s
γ) 0 1 2 3 4 5 6 7 8 9 10
κ δ κ δ κ δ
στο 4 cm και στο 8 cm
2009
ΘΕΜΑ Γ
y = 0,4 ημ2π(2t - 0,5x) S.I. y = 0,4 ημ2π(t/T - x/λ) λ = 2 m f = 2 Hz T = 0,5 s ω = 2πf = 4π rad/s v = λ / T = 4 m/s ταχύτητα διαδόσεως του κύματος
v = 1,6π ημ2π(2t - 0,5x) α = - 6,4π ημ2π(2t - 0,5x)
διαφορά φάσης δύο σημείων που απέχουν 1,5m : Δφ / Δx = 2π / λ => Δφ / 1,5m = 2π / 2m => Δφ = 3π/2 rad
στιγμιότυπο κύματος t1 = 11/8 s y = 0,4 ημ2π(2⋅11/8 - 0,5x) = 0,4 ημ(11π/2 - πx) = - 0,4 συν(πx)
x = 11/8 s 4 m/s = 5,5 m = 2m + 2m + 1,5m = λ + λ + 3λ/4

2010
Α3. Μεταξύ δύο διαδοχικών δεσμών στάσιμου κύματος τα σημεία του ελαστικού μέσου
α. έχουν το ίδιο πλάτος ταλάντωσης.
β. έχουν την ίδια φάση.
γ. έχουν την ίδια ταχύτητα ταλάντωσης.
δ. είναι ακίνητα.
Β1. Στην ελεύθερη επιφάνεια ενός υγρού δύο σύγχρονες πηγές αρμονικών κυμάτων εκτελούν κατακόρυφες ταλαντώσεις με συχνότητα f και δημιουργούν εγκάρσια κύματα ίδιου πλάτους Α. Ένα σημείο Σ της επιφάνειας του υγρού ταλαντώνεται εξ αιτίας της συμβολής των δύο κυμάτων με πλάτος 2Α. Αν οι δύο πηγές εκτελέσουν ταλάντωση με συχνότητα 2f και με το ίδιο πλάτος Α, τότε το σημείο Σ θα
α. ταλαντωθεί με πλάτος 2Α.
β. ταλαντωθεί με πλάτος 4Α.
y = y1 + y2 = A ημ(2πft - 2πr1/λ) + A ημ(2πft - 2πr2/λ) = 2A συν {π(r1 - r2)/λ} ημ{2πft - π(r1 + r2)/λ}
y' = A ημ(2π2ft - 2πr1/λ) + A ημ(2π2ft - 2πr2/λ) = 2A συν {π(r1 - r2)/λ} ημ{2π2ft - π(r1 + r2)/λ} (α)
Β2. ∆ίσκος μάζας Μ είναι στερεωμένος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, και ισορροπεί. Το άλλο άκρο του ελατηρίου είναι στερεωμένο στο έδαφος.
Στο δίσκο τοποθετούμε χωρίς αρχική ταχύτητα σώμα μάζας m. Το σύστημα εκτελεί απλή αρμονική ταλάντωση. Η ενέργεια της ταλάντωσης είναι
α. ½ m2 g2 / k β. ½ Μ2 g2 / k γ. ½ (m+Μ)2 g2 / k
ισορροπία δίσκου - σώματος : (m + M) g = k Δl => Δl = (m + M) g / k είναι το πλάτος της ταλάντωσης διότι αρχικά το σύστημα δεν έχει ταχύτητα άρα είναι στο άνω άκρο της ταλάντωσής του
η ενέργεια του συστήματος είναι Ε = ½ k Α2 = ½ k (m + M)2 g2 / k2 = ½ (m + M)2 g2 / k (γ)
Β3. ∆ύο σώματα με μάζες m1=2 kg και m2=3 kg κινούνται χωρίς τριβές στο ίδιο οριζόντιο επίπεδο και σε κάθετες διευθύνσεις με ταχύτητες υ1=4 m/s και υ2=2 m/s και συγκρούονται πλαστικά. Η κινητική ενέργεια του συσσωματώματος είναι: α. 5 J β. 10 J γ. 20 J
m12v12 + m22v22 = (m1 + m2)2u2 => 2242 + 3222 = (2 + 3)2u2 => 4 52 = 52 u2 => u = 2 m/s
K = ½ (m1 + m2) u2 = ½ 5 22 = 10 J (β)
2011
Β1. ∆ύο όμοια ιδανικά ελατήρια κρέμονται από δύο ακλόνητα σημεία. Στα κάτω άκρα των ελατηρίων δένονται σώματα Σ1 μάζας m1 και Σ2 μάζας m2. Κάτω από το σώμα Σ1 δένουμε μέσω αβαρούς νήματος άλλο σώμα μάζας m2, ενώ κάτω από το Σ2 σώμα μάζας m1 (m1≠m2), όπως φαίνεται στο σχήμα. 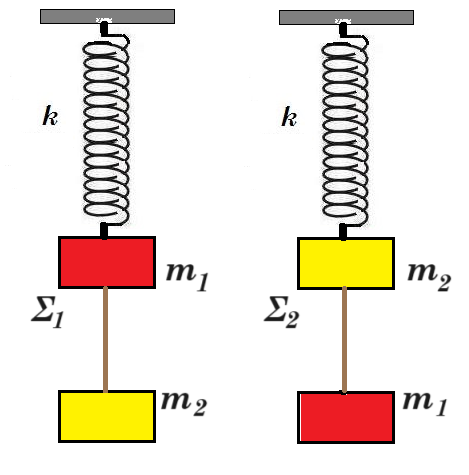 Αρχικά τα σώματα είναι ακίνητα. Κάποια στιγμή κόβουμε τα νήματα και τα σώματα Σ1 και Σ2 αρχίζουν να ταλαντώνονται. Αν η ενέργεια της ταλάντωσης του Σ1 είναι Ε1 και του Σ2 είναι Ε2, τότε:
Αρχικά τα σώματα είναι ακίνητα. Κάποια στιγμή κόβουμε τα νήματα και τα σώματα Σ1 και Σ2 αρχίζουν να ταλαντώνονται. Αν η ενέργεια της ταλάντωσης του Σ1 είναι Ε1 και του Σ2 είναι Ε2, τότε:
α. E1/E2 = m2/m1 β. E1/E2 = m22 / m12 γ. E1/E2 = 1
ισορροπία Σ1 - Σ2 : (m1 + m2) g = k Δl1,2 => Δl1,2 = (m1 + m2) g / k
ισορροπία Σ1 : m1 g = k Δl1 => Δl1 = m1 g / k πλάτος ταλάντωσης Σ1 : Α1 = Δl1,2 - Δl1 = m2 g / k
ισορροπία Σ2 : m2 g = k Δl2 => Δl2 = m2 g / k πλάτος ταλάντωσης Σ2 : Α2 = Δl1,2 - Δl2 = m1 g / k
ενέργεια ταλάντωσης Σ1 : Ε1 = ½ k Α12 = ½ k ( m2 g / k )2
ενέργεια ταλάντωσης Σ2 : Ε2 = ½ k Α22 = ½ k ( m1 g / k )2 Ε1/Ε2 = m22 / m12 (β)
Β3. ∆ύο σώματα, το Α με μάζα m1 και το Β με μάζα m2, είναι διαρκώς σε επαφή και κινούνται σε λείο οριζόντιο επίπεδο με την ίδια ταχύτητα υ. Τα σώματα συγκρούονται κεντρικά με σώμα Γ μάζας 4m1, το οποίο αρχικά είναι ακίνητο. 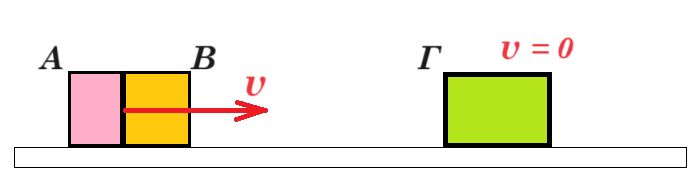 Μετά την κρούση το Α σταματά, ενώ το Β κολλάει στο Γ και το συσσωμάτωμα αυτό κινείται με ταχύτητα υ/3.
Μετά την κρούση το Α σταματά, ενώ το Β κολλάει στο Γ και το συσσωμάτωμα αυτό κινείται με ταχύτητα υ/3.
Τότε θα ισχύει: α. m1/m2 = 2 β. m1/m2 = 1/2 γ. m1/m2 = 1
διατήρηση ορμής : (m1 + m2) υ = (m2 + 4m1) υ/3 => m1 + m2 = (m2 + 4m1)/3 =>
=> 3m1 + 3m2 = m2 + 4m1 => 2m2 = m1 => m1 / m2 = 2 (α)
ΘΕΜΑ Γ
Στην επιφάνεια ενός υγρού που ηρεμεί, βρίσκονται δύο σύγχρονες σημειακές πηγές Π1 και Π2, που δημιουργούν στην
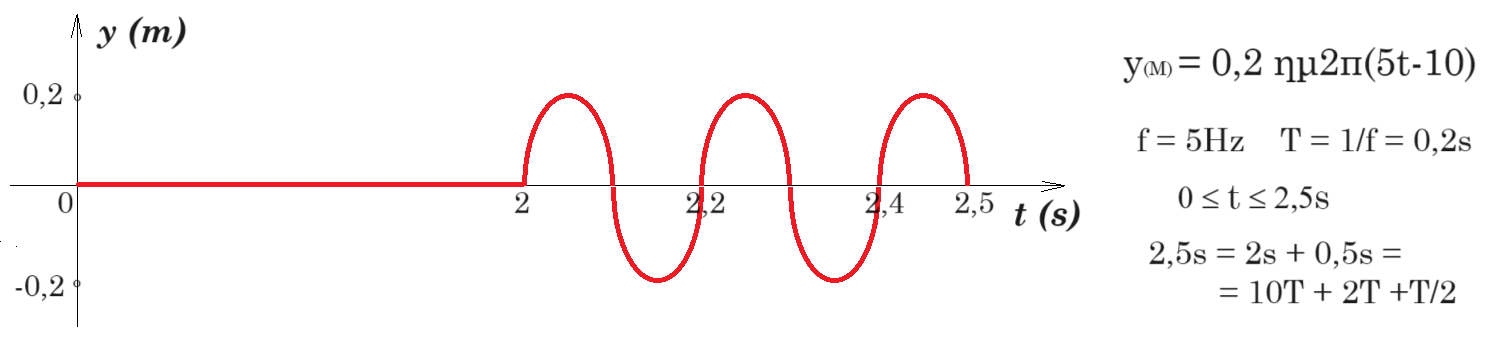
επιφάνεια του υγρού εγκάρσια αρμονικά κύματα ίσου πλάτους. Οι πηγές αρχίζουν να ταλαντώνονται τη χρονική στιγμή t0=0 ξεκινώντας από τη θέση ισορροπίας τους και κινούμενες προς την ίδια κατεύθυνση, την οποία θεωρούμε θετική. Η χρονική εξίσωση της ταλάντωσης ενός σημείου Μ, που βρίσκεται στη μεσοκάθετο του ευθύγραμμου τμήματος Π1Π2, μετά τη συμβολή των κυμάτων δίνεται στο S.I. από τη σχέση: yM=0,2ημ2π(5t-10).
Η ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού είναι υ=2 m/s. Έστω Ο το μέσο του ευθύγραμμου τμήματος Π1Π2 και d=1m η απόσταση μεταξύ των πηγών.
Γ1. Να βρείτε την απόσταση ΜΠ1 και τη διαφορά φάσης των ταλαντώσεων των σημείων Ο και Μ.
Γ2. Πόσα σημεία του ευθυγράμμου τμήματος Π1Π2 ταλαντώνονται με μέγιστο πλάτος; Σχεδιάστε τη γραφική παράσταση της απομάκρυνσης του σημείου Μ συναρτήσει του χρόνου t για 0≤t≤2,5s.
Γ1. yM=0,2ημ2π(5t-10) = 0,2 ημ(10πt - 20π) f = 5 Hz x/λ = 10 v = λ f => λ = 2 m/s / 5 Hz => λ = 0,4 m οπότε x = 4 m = απόσταση του Μ από την πηγή Π1 αλλά και από την πηγή Π2
yΜ = y1 + y2 = A ημ(2πft - 2πx/λ) + A ημ(2πft - 2πx/λ) = 2A ημ{2πft - 2πx/λ} = 0,2 ημ2π(5t - 10) A = 0,1 m
yO = y1 + y2 = A ημ(2πft - 2πx/λ) + A ημ(2πft - 2πx/λ) = 2A ημ{2πft - 2πx/λ} = 0,2 ημ{2π 5t - 2π 0,5 / 0,4} =
= 0,2 ημ 2π(5t - 5/4) = 0,2 ημ(10πt - 2,5π)
φΟ - φΜ = 10πt - 2,5π - (10πt - 20π) = 17,5π rad
Γ2. συν {π(r1 - r2)/λ} = ± 1 => r1 - r2 = Νλ (1) r1 + r2 = d (2)
(1) + (2) => 2 r1 = Νλ + d => r1 = Νλ/2 + d/2 = Ν 0,4/2 + 1/2 = Ν 0,2 + 0,5
0 £ r1 £ d => 0 £ Ν 0,2 + 0,5 £ 1 => -0,5 £ Ν 0,2 £ 0,5 => -2,5 £ Ν £ 2,5 Ν = -2,-1,0,1,2
2012 τροποποίηση
ΘΕΜΑ Γ
Ομογενής και ισοπαχής δοκός (ΟΑ), μάζας M=6 kg και μήκους l=0,3 m, μπορεί να στρέφεται χωρίς τριβές σε κατακόρυφο επίπεδο γύρω από οριζόντιο άξονα που περνά από το ένα άκρο της Ο. Στο άλλο της άκρο Α υπάρχει στερεωμένη μικρή σφαίρα μάζας m. Ασκούμε στο άκρο Α δύναμη, σταθερού μέτρου F = 120/π N, που είναι συνεχώς κάθετη στη δοκό. 
Γ1. Βρείτε το έργο της δύναμης F κατά την περιστροφή του συστήματος μέχρι την οριζόντια θέση της. Μονάδες 6
Γ2. Βρείτε την μάζα m της σφαίρας έτσι ώστε η γωνιακή ταχύτητα του συστήματος δοκού-σφαίρας στην οριζόντια θέση να ισούται με μηδέν. Μονάδες 6
Γ3. Βρείτε την κινητική ενέργεια του συστήματος μέχρις ότου η δοκός έρθει σε κατακόρυφη θέση. Τη στιγμή αυτή καταργείται η δύναμη F. Μονάδες 6
Επαναφέρουμε το σύστημα δοκού-σφαίρας στην αρχική κατακόρυφη θέση του. Ασκούμε στο άκρο Α δύναμη, σταθερού μέτρου F1 = 30 Ν, που είναι συνεχώς κάθετη στη δοκό.
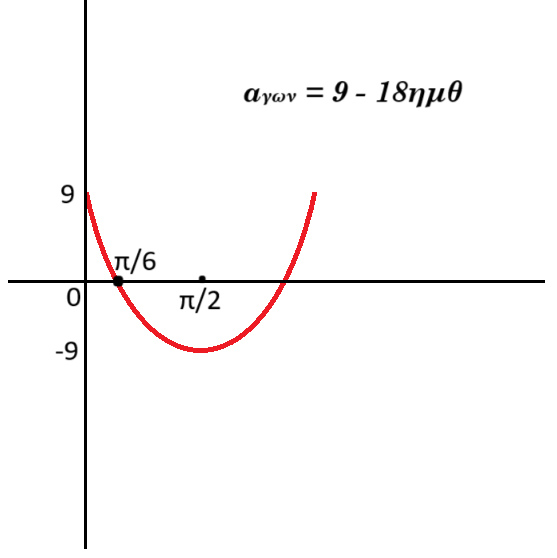
Γ4. Βρείτε τη γωνία θ που σχηματίζει η δοκός με την κατακόρυφο τη στιγμή που η κινητική ενέργεια της σφαίρας γίνεται μέγιστη. Τη στιγμή αυτή καταργείται η δύναμη F1. Η γωνιακή επιτάχυνση αγων της δοκού συναρτήσει της γωνίας θ δίνεται από την σχέση : 0,45 αγων = 9 - 18ημθ
Γ5. Εάν θ = 30° βρείτε την συνολική ροπή ως προς το άκρο Ο της δοκού που δέχεται το σύστημα δοκός-σφαίρα. Τι παρατηρείτε;
ροπή αδράνειας δοκού - σφαίρας ως προς τον άξονα περιστροφής που διέρχεται από το Ο : Ιολικό = 1/3 Μ l2 + m l2 = 1/3 6 0,09 + 3 0,09 = 0,18 + 0,27 = 0,45 kg.m2
ροπές ως προς το Ο : Στ(Ο) = 30 0,3 - 60 0,15 ημθ - 30 0,3 ημθ = 9 - 9 ημθ - 9 ημθ = 9 - 18 ημθ
Στ(Ο) = Ιολικό αγων => 9 - 18 ημθ = 0,45 αγων
Γ1. η δύναμη F είναι συνεχώς κάθετη στη δοκό άρα ο φορέας της είναι ευθεία εφαπτομένη στην τροχιά της σφαίρας οπότε το έργο που προσφέρει : WF = F s = F l φ = F l π/2 = 120/π 0,3 π/2 = 18 Joule η δοκός στρέφεται κατά γωνία 90°
Γ2. εφ' όσον η γωνιακή ταχύτητα είναι μηδέν, στην οριζόντια θέση, η ταχύτητα της σφαίρας είναι ίση με μηδέν
διατήρηση ενέργειας το έργο που προσφέρει η δύμαμη F μετατρέπεται σε δυναμική ενέργεια της δοκού και της σφαίρας :
WF = Mg l/2 + mg l => 18 = 60 0,15 + m 10 0,3 => 18 - 9 = m 3 => m = 3 kg μάζα της σφαίρας
Γ3. η δοκός σε κατακόρυφη θέση
WF = F l π = 120/π 0,3 π = 36 J
Mg l + mg 2l = 60 0,3 + 30 0,6 = 36 J = WF => K = 0
Γ4. η κινητική ενέργεια της σφαίρας γίνεται μέγιστη τη στιγμή που η ταχύτητά της γίνεται μέγιστη άρα η γωνιακή της ταχύτητα γίνεται μέγιστη συνεπώς η γωνιακή επιτάχυνση μηδενίζεται οπότε 9 - 18ημθ = 0 => ημθ = 1/2 => θ = 30°
Γ5. Στ(Ο) = F1 l - Mg l/2 ημ30° - mg l ημ30° = 30 0,3 - 60 0,15 ½ - 30 0,3 ½ = 9 - 4,5 - 4,5 => Στ(Ο) = 0
2013
Β2. Δύο σύγχρονες πηγές κυμάτων Π1 και Π2 που βρίσκονται αντίστοιχα στα σημεία Κ και Λ της επιφάνειας υγρού παράγουν πανομοιότυπα εγκάρσια αρμονικά κύματα με ίδιο πλάτος, ίσες συχνότητες f1 και ίσα μήκη κύματος λ1. Αν η απόσταση των σημείων Κ και Λ είναι d = 2 λ1, τότε δημιουργούνται τέσσερις υπερβολές απόσβεσης, μεταξύ των σημείων Κ και Λ. Αλλάζοντας την συχνότητα των δύο πηγών σε f2 = 3 f1 και διατηρώντας το ίδιο πλάτος, ο αριθμός των υπερβολών απόσβεσης, που δημιουργούνται μεταξύ των δύο σημείων Κ και Λ, είναι: α) 6 β) 8 γ) 12
υ = λ1 f1 = λ2 f2 => λ1 f1 = λ2 3f1 => λ1 = 3λ2 οπότε (ΚΛ) = 2 λ1 = 6 λ2
r1 - r2 = Νλ2 + λ2/2 (1) r1 + r2 = d (2)
(1) + (2) => 2 r1 = Νλ2 + λ2/2 + d => r1 = Νλ2 /2 + λ2/4 + 6 λ2 /2 = Νλ2 /2 + 13/4 λ2
0 £ r1 £ d => 0 £ Νλ2 /2 + 13/4 λ2 £ 6 λ2 => - 13/4 λ2 £ Ν λ2 /2 £ 11/4 λ2 => - 13/2 £ Ν £ 11/2 Ν = -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 12 υπερβολές απόσβεσης
Θέμα Γ
Σώμα Σ1 με μάζα m1 κινείται σε οριζόντιο επίπεδο ολισθαίνοντας προς άλλο σώμα Σ2 με μάζα m2 = 2 m1, το οποίο αρχικά είναι ακίνητο. Έστω υ0 η ταχύτητα που έχει το σώμα Σ1 τη στιγμή t0 = 0 και ενώ βρίσκεται σε απόσταση d = 1 m από το σώμα Σ2. Αρχικά, θεωρούμε ότι το σώμα Σ2 είναι ακίνητο πάνω στο επίπεδο δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου με αμελητέα μάζα και σταθερά ελατηρίου k, και το οποίο έχει το φυσικό του μήκος ℓ0. Το δεύτερο άκρο του ελατηρίου είναι στερεωμένο σε ακλόνητο τοίχο, όπως φαίνεται στο σχήμα: 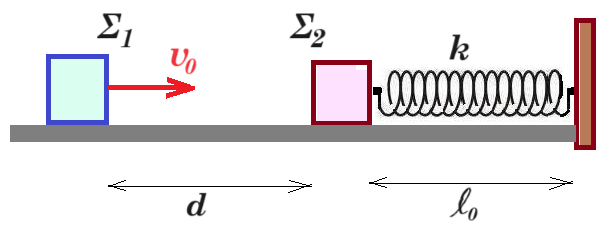 Αμέσως μετά τη κρούση, που είναι κεντρική και ελαστική, το σώμα Σ1 αποκτά ταχύτητα με μέτρο υ1' = √10 m/s και φορά αντίθετη της αρχικής ταχύτητας.
Αμέσως μετά τη κρούση, που είναι κεντρική και ελαστική, το σώμα Σ1 αποκτά ταχύτητα με μέτρο υ1' = √10 m/s και φορά αντίθετη της αρχικής ταχύτητας.
Δίνεται ότι ο συντελεστής τριβής ολίσθησης των δύο σωμάτων με το οριζόντιο επίπεδο είναι μ = 0,5 και ότι η επιτάχυνση της βαρύτητας είναι g = 10 m/s2.
Γ1. Να υπολογίσετε την αρχική ταχύτητα υ0 του σώματος Σ1 και το ποσοστό της κινητικής ενέργειας που μεταφέρθηκε από το σώμα Σ1 στο σώμα Σ2 κατά την κρούση.
Γ2. Να υπολογίσετε το συνολικό χρόνο κίνησης του σώματος Σ1 από την αρχική χρονική στιγμή t0 μέχρι να ακινητοποιηθεί τελικά.
Γ3. Να υπολογίσετε τη μέγιστη συσπείρωση του ελατηρίου, αν δίνεται ότι m2 = 1kg και k = 105 N/m.
Θεωρήστε ότι η χρονική διάρκεια της κρούσης είναι αμελητέα και ότι τα δύο σώματα συγκρούονται μόνο μία φορά.
2014
Β1. Δύο όμοια σώματα, ίσων μαζών m το καθένα, συνδέονται με όμοια ιδανικά ελατήρια σταθεράς k το καθένα, των οποίων τα άλλα άκρα είναι συνδεδεμένα σε ακλόνητα σημεία, όπως στο σχήμα. Οι άξονες των δύο ελατηρίων βρίσκονται στην ίδια ευθεία, τα ελατήρια βρίσκονται στο φυσικό τους μήκος ℓ0 και το οριζόντιο επίπεδο στο οποίο βρίσκονται είναι λείο. 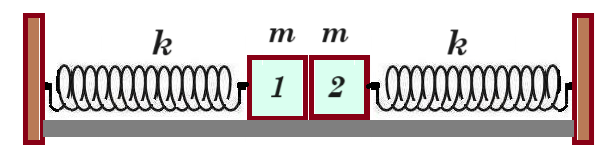 Μετακινούμε το σώμα 1 προς τα αριστερά κατά d και στη συνέχεια το αφήνουμε ελεύθερο να κινηθεί. Το σώμα 1 συγκρούεται πλαστικά με το σώμα 2. Το συσσωμάτωμα που προκύπτει εκτελεί απλή αρμονική ταλάντωση με σταθερά επαναφοράς D = 2k. Αν Α1 το πλάτος της ταλάντωσης του σώματος 1 πριν τη κρούση και Α2 το πλάτος της ταλάντωσης του συσσωματώματος μετά την κρούση, τότε ο λόγος Α1/Α2 είναι: α) 1/2 β) 1 γ) 2
Μετακινούμε το σώμα 1 προς τα αριστερά κατά d και στη συνέχεια το αφήνουμε ελεύθερο να κινηθεί. Το σώμα 1 συγκρούεται πλαστικά με το σώμα 2. Το συσσωμάτωμα που προκύπτει εκτελεί απλή αρμονική ταλάντωση με σταθερά επαναφοράς D = 2k. Αν Α1 το πλάτος της ταλάντωσης του σώματος 1 πριν τη κρούση και Α2 το πλάτος της ταλάντωσης του συσσωματώματος μετά την κρούση, τότε ο λόγος Α1/Α2 είναι: α) 1/2 β) 1 γ) 2
A1 = d ω2 = k/m => ω = √(k/m) v = ω Α1 = √(k/m) Α1
m v = (m + m) u => u = v/2 (ω')2 = 2k / 2m = k/m => ω' = √(k/m) = ω u = ω' Α2 = √(k/m) Α2
v = 2 u => √(k/m) Α1 = 2 √(k/m) Α2 => A1 = 2 A2 (γ)
Β3. Σε λείο οριζόντιο επίπεδο και σε διεύθυνση κάθετη σε κατακόρυφο τοίχο κινείται σφαίρα μάζας m1 με ταχύτητα μέτρου υ1. Κάποια χρονική στιγμή η σφαίρα μάζας m1 συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα μάζας m2 (m2 > m1). Μετά την κρούση με τη μάζα m1, η m2 συγκρούεται ελαστικά με τον τοίχο.
 Παρατηρούμε ότι η απόσταση των μαζών m1 και m2, μετά την κρούση της m2 με τον τοίχο, παραμένει σταθερή. Ο λόγος των μαζών m1 / m2 είναι: α) 1/3 β) 1 γ) 3
Παρατηρούμε ότι η απόσταση των μαζών m1 και m2, μετά την κρούση της m2 με τον τοίχο, παραμένει σταθερή. Ο λόγος των μαζών m1 / m2 είναι: α) 1/3 β) 1 γ) 3
v1' = v1 (m1 - m2) / (m1 + m2) < 0 προς τα αριστερά διότι m1 < m2
v2' = 2 v1 m1 / (m1 + m2) > 0 προς τα δεξιά μετά η m2 συγκρούεται ελαστικά με τον τοίχο και αποκτά ταχύτητα v2'' = - v2' = - 2 v1 m1 / (m1 + m2) προς τα αριστερά
επειδή η απόσταση των σφαιρών παραμένει σταθερή ισχύει v1' = v2'' =>
=> v1 (m1 - m2) / (m1 + m2) = - 2 v1 m1 / (m1 + m2) => m1 - m2 = - 2 m1 => 3m1 = m2 (a)
Θέμα Γ
Δύο σύγχρονες σημειακές πηγές Π1 και Π2 δημιουργούν στην επιφάνεια υγρού εγκάρσια κύματα που διαδίδονται με ταχύτητα υ = 5 m/s. Μικρό κομμάτι φελλού βρίσκεται σε κάποιο σημείο Σ της επιφάνειας πλησιέστερα στην πηγή Π2. Η απομάκρυνση του σημείου Σ από τη θέση ισορροπίας του σε συνάρτηση με τον χρόνο περιγράφεται από τη γραφική παράσταση του σχήματος. Οι πηγές αρχίζουν να ταλαντώνονται τη χρονική στιγμή t0 = 0 και εκτελούν ταλαντώσεις της μορφής y = Α⋅ημωt. 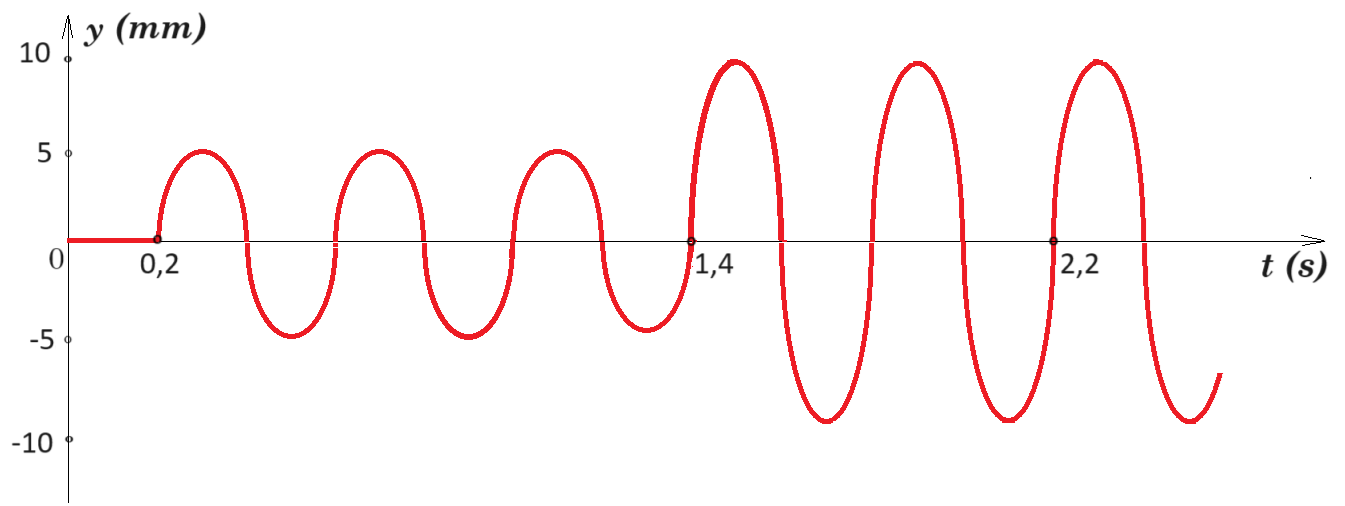 Γ1. Να βρείτε τις αποστάσεις r1 και r2 του σημείου Σ από τις πηγές Π1 και Π2, αντίστοιχα.
Γ1. Να βρείτε τις αποστάσεις r1 και r2 του σημείου Σ από τις πηγές Π1 και Π2, αντίστοιχα.
Γ2. Να γράψετε τη σχέση που δίνει την απομάκρυνση του φελλού από τη θέση ισορροπίας του σε συνάρτηση με τον χρόνο, για t ≥ 0.
Γ3. Ποιο είναι το μέτρο της ταχύτητας ταλάντωσης του φελλού κάποια χρονική στιγμή t1, κατά την οποία η απομάκρυνσή του από τη θέση ισορροπίας του είναι y1 = 5√3⋅10-3 m ;
Γ4. Έστω Κ1 η μέγιστη κινητική ενέργεια του φελλού μετά τη συμβολή.
Αλλάζουμε τη συχνότητα των ταλαντώσεων των πηγών Π1 και Π2 έτσι ώστε η συχνότητά τους να είναι ίση με τα 10/9 της αρχικής τους συχνότητας. Αν μετά τη νέα συμβολή η μέγιστη κινητική ενέργεια του φελλού είναι Κ2, να βρεθεί ο λόγος Κ1/Κ2.
Γ1. 3Τ = 1,4s - 0,2s = 1,2s => T = 0,4s f = 1/T = 2,5 Hz ω = 2πf = 5π rad/s
v = λ f => λ = 5 m/s / 2,5 Hz = 2 m r1 = 5 m/s 0,2 s = 1 m r2 = 5 m/s 1,4 s = 7 m
Γ2. {0 , 0,2s] y = 0
[0,2s , 1,4s] y = 5⋅10-3 ημ5π(t - 0,2) v = 25π⋅10-3 συν5π(t - 0,2)
[1,4s , ...) y = 10⋅10-3 ημ5π(t - 1,4) v = 50π⋅10-3 συν5π(t - 1,4) = 0,05π συν5π(t - 1,4)
Γ3. y = 5√3⋅10-3 = 10⋅10-3 ημ5π(t - 1,4) => ημ5π(t - 1,4) = √3/2 τότε συν5π(t - 1,4) = ± 0,5
τότε v = 50π⋅10-3 συν5π(t - 1,4) = 50π⋅10-3 (±0,5) => v = ± 25π⋅10-3 m/s
Γ4. Κ1 = ½ m v2 = ½ m { 0,05π συν5π(t - 1,4) }2 = ½ m 0,052 π2 συν2(5πt - 7π)
f ' = 10/9 2,5 Hz = 25/9 Hz λ' = v / f ' = 5 m/s / (25/9 Hz) => λ' = 9/5 m
y = 10⋅10-3 ημ5π(t - 1,4)
y = y1 + y2 = A ημ(2πf 't - 2πr1/λ') + A ημ(2πf 't - 2πr2/λ') = 2A συν{π(r1 - r2)/λ'} ημ{2πf 't - π(r1 + r2)/λ'] =
= 10⋅10-3 συν { π(1 - 7) / (9/5) } ημ{ 2π 25/9 t - π(1 + 7) / (9/5) ] => y = 10-2 συν{-10π/3} ημ{ 50π/9 t - 40π/9 ]
v = 50π/9 10-2 συν{-10π/3} συν{50π/9 t - 40π/9] = π/18 (-0,5) συν{50π/9 t - 40π/9] =
= - π/36 συν{50π/9 t - 40π/9]
Κ2 = ½ m v2 = ½ m { - π/36 συν{50π/9 t - 40π/9] }2 = ½ m (π/36)2 συν2{50π/9 t - 40π/9]
Κ1,max / K2,max = 0,052 π2 / (π/36)2 = ( 0,05 36 )2 = 1,82 = ( 9/5 )2 = 81/25
2015
Από το εσωτερικό άκρο Α ενός ημισφαιρίου ακτίνας R= 1,6m αφήνεται να κυλήσει μία συμπαγής μικρή σφαίρα μάζας m=1,4kg και ακτίνας r = R/8. Το ημισφαίριο είναι βυθισμένο στο έδαφος, όπως φαίνεται στο σχήμα και η κίνηση της σφαίρας γίνεται χωρίς ολίσθηση.
Δ1. Να εκφράσετε τη στατική τριβή T που ασκείται στη σφαίρα σε συνάρτηση με το συνημίτονο της γωνίας φ που σχηματίζει η ακτίνα ΟΓ του ημισφαιρίου με την ευθεία ΑΕ της επιφάνειας του εδάφους.
Δ2. Να υπολογίσετε την κάθετη δύναμη που ασκεί η ημισφαιρική επιφάνεια στη σφαίρα όταν αυτή βρίσκεται στο σημείο Γ όπου φ = 30° .
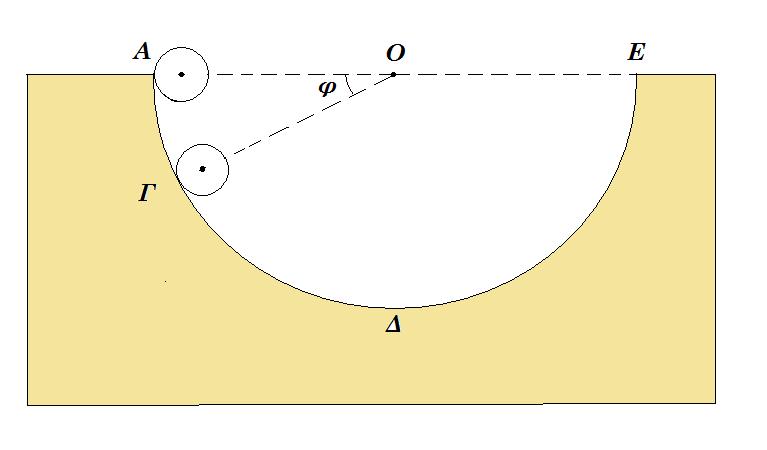 Μια άλλη σφαίρα, όμοια με την προηγούμενη, εκτοξεύεται από το κατώτατο σημείο Δ του ημισφαιρίου με ταχύτητα υ = 6m/s και κυλίεται χωρίς ολίσθηση στο εσωτερικό του με κατεύθυνση το άκρο Ε.
Μια άλλη σφαίρα, όμοια με την προηγούμενη, εκτοξεύεται από το κατώτατο σημείο Δ του ημισφαιρίου με ταχύτητα υ = 6m/s και κυλίεται χωρίς ολίσθηση στο εσωτερικό του με κατεύθυνση το άκρο Ε.
Δ3. Να υπολογίσετε το μέγιστο ύψος από την επιφάνεια του εδάφους που θα φτάσει η σφαίρα κατά την κίνησή της.
Δ4. Να υπολογίσετε το ρυθμό μεταβολής της κινητικής ενέργειας και το ρυθμό μεταβολής της στροφορμής της σφαίρας, αμέσως μόλις αυτή χάσει την επαφή με την επιφάνεια του ημισφαιρίου στο σημείο Ε.
Δ1.
Στ(Κ) = Ι(Κ) αγων => Τ r = 2/5 m r2 αγων => Τ = 2/5 m r αγων => Τ = 2/5 m α r αγων = a
ΣF = m a => m g συνφ - Τ = m a => m g συνφ = 2/5 m α + m a = 7/5 m α => 5/7 g συνφ = α
Τ = 2/7 m g συνφ = 2/7 1,4 10 συνφ => Τ = 4 συνφ
Δ2. διατήρηση ενέργειας Α ® Γ : m g h = ½ m v2 + ½ Ι(Κ) ω2 =>
=> m g (R - r)ημφ = ½ m v2 + ½ 2/5 m r2 ω2 =>
=> g (R - r)ημφ = ½ v2 + 1/5 v2 = 7/10 v2 => 10/7 g (R - r)ημφ = v2
ΣF = Fκ => Ν - m g ημφ = m υ2 / (R - r) => Ν = m g ημφ + m 10/7 g ημφ =>
=> Ν = 17/7 m g ημφ = 17/7 1,4 10 1/2 => Ν = 17 Ν
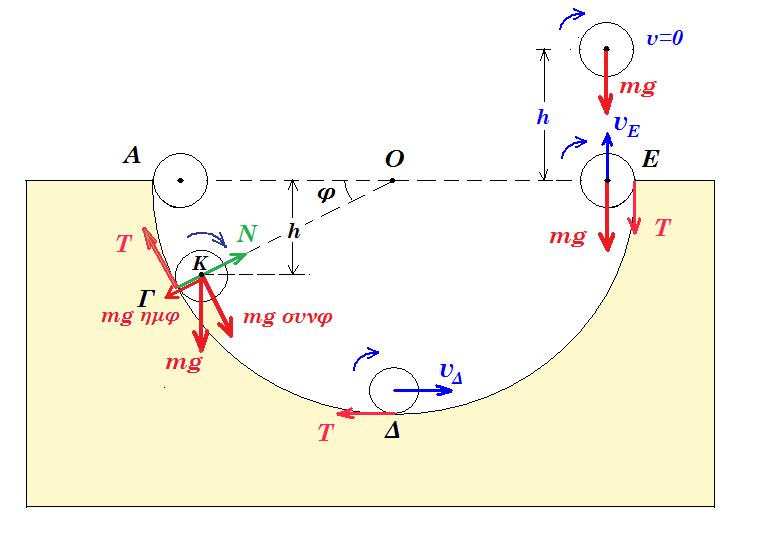
Δ3. διατήρηση ενέργειας Δ ® Ε : ½ m vΔ2 + ½ Ι(Κ) ω2 = m g (R - r) + ½ m vΕ2 + ½ Ι(Κ) ω2 =>
=> ½ m vΔ2 + ½ 2/5 m r2 ω2 = m g (R - R/8) + ½ m vΕ2 + ½ 2/5 m r2 ω2 =>
=> ½ vΔ2 + 1/5 vΔ2 = g 7/8 R + ½ vΕ2 + 1/5 vΕ2 =>
=> 7/10 vΔ2 = 7/8 R g + 7/10 vΕ2 => vΔ2 = 10/8 R g + vΕ2 =>
=> 36 - 5/4 1,6 10 = vΕ2 => vΕ2 = 36 - 20 = 16 => vΕ = 4m/s
στο σημείο Ε : ω = vΕ / r = 4 / 0,2 = 20 rad/s
όταν η σφαίρα εγκαταλήψει το ημικύκλιο στο σημείο Ε συνεχίζει να περιστρέφεται με την ίδια γωνιακή ταχύτητα ω = 20 rad/s διότι δεν ασκείται δύναμη που να δημιουργεί ροπή ( η σφαίρα είναι στον αέρα ενεργεί μόνο το βάρος της ) Στ(Κ) = 0
m g h + ½ Ι(Κ) ω2 = ½ m vΕ2 + ½ Ι(Κ) ω2 => m g h = ½ m vΕ2 =>
=> g h = ½ vΕ2 => h = ½ 16 / 10 => h = 0,8 m
Δ4. όταν η σφαίρα εγκαταλείπει το ημικύκλιο στο σημείο Ε
(dK / dt)μεταφορική = P = F . v = - mg vE = - 1,4 10 4 = - 56 J/s
(dK / dt)περιστροφική = Στ(Κ) . ω(Ε) = 0 . 20 rad/s = 0
ο ρυθμός μεταβολής της στροφορμής : dL/dt = Στ(Κ) = 0
2017
Μία ομογενής άκαμπτη ράβδος ΑΓ σταθερής διατομής έχει μάζα Μ=4Kg. Η ράβδος ισορροπεί σε οριζόντια θέση και το άκρο της Α συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Το άλλο άκρο Γ της ράβδου συνδέεται μέσω αβαρούς μη εκτατού νήματος ΓΔ με τον κατακόρυφο τοίχο. Το νήμα σχηματίζει με τη ράβδο γωνία φ. Γύρω από ένα λεπτό ομογενή δίσκο κέντρου Κ, μάζας m=2kg και ακτίνας R=0,1m είναι τυλιγμένο πολλές φορές ένα λεπτό μη εκτατό αβαρές νήμα. Το ελεύθερο άκρο του νήματος έχει στερεωθεί στο άκρο Γ της ράβδου ΑΓ, όπως φαίνεται στο σχήμα
Τη χρονική στιγμή t0=0 ο δίσκος αφήνεται να κινηθεί και το νήμα ξετυλίγεται χωρίς να ολισθαίνει.
Δ1. Να υπολογίσετε το μέτρο της επιτάχυνσης του κέντρου μάζας του δίσκου, καθώς αυτός κατέρχεται.
Δ2. Να υπολογίσετε το μέτρο της δύναμης που δέχεται η ράβδος ΑΓ στο άκρο της Γ από το νήμα ΓΔ, όταν ο δίσκος κατέρχεται καθώς και την δύναμη που δέχεται η ράβδος ΑΓ στο άκρο της Α από την άρθρωση.
Τη χρονική στιγμή που το κέντρο μάζας Κ του δίσκου έχει κατέλθει κατακόρυφα κατά h1=0,3m το νήμα που συνδέει το δίσκο με τη ράβδο κόβεται.
Δ3. Να υπολογίσετε το μέτρο της στροφορμής του δίσκου ως προς τον άξονα περιστροφής του, μετά από χρονικό διάστημα Δt από τη στιγμή που κόπηκε το νήμα.
Δ4. Να υπολογίσετε το λόγο της κινητικής ενέργειας λόγω περιστροφικής κίνησης προς την κινητική ενέργεια λόγω μεταφορικής κίνησης του δίσκου μετά από χρονικό διάστημα Δt ́=0,1s από τη στιγμή που κόπηκε το νήμα.
Δίνονται: η επιτάχυνση της βαρύτητας g = 10 m/s2 ημφ = 0,8 και συνφ = 0,6 ο άξονας περιστροφής του δίσκου παραμένει συνεχώς οριζόντιος και κινείται σε κατακόρυφη τροχιά σε όλη τη διάρκεια της κίνησης του, ο δίσκος δεν φτάνει στο έδαφος στη διάρκεια του φαινομένου.
Δ1.
ροπές ως προς Κ : T1 R = I αγων => T1 R = ½ m R2 αγων => T1 = ½ m R αγων = ½ m α
mg - T1 = m a => mg = ½ m α + m a = 3/2 m α => a = 2g/3 => a = 20/3 m/s2
αγων = α / R = 20/3 / 0,1 => αγων = 200/3 rad/s2 T1 = ½ m α = ½ 2 20/3 => Τ1 = 20/3 N
Δ2.
ροπές ως προς Α : M g l/2 + T1 l - T2 ημφ l = 0 => 4 10 /2 + 20/3 - T2 0,8 = 0 =>
=> 20 + 20/3 = T2 0,8 => T2 = 80/3 / 0,8 => T2 = 100/3 Ν
ΣFx = 0 => FAx = T2x = T2 συνφ => FAx = 100/3 0,6 = 20 Ν
ΣFy = 0 => FAy + T2y = T1 + Mg =>
=> FAy = - T2 ημφ + T1 + Mg = - 100/3 0,8 + 20/3 + 40 => FAy = 20 Ν
FA2 = FAx2 + FAy2 = 202 + 202 => FA = 20 2½ Ν
Δ3.
h = ½ a t2 => 0,3 = ½ 20/3 t2 => t = 0,3 s τότε υ = α t = 20/3 0,3 = 2 m/s
ω = αγων t = 200/3 0,3 = 20 rad/s = σταθερή διότι από τη στιγμή που κόβεται το νήμα δεν δέχεται ροπή ο δίσκος Τ1 = 0
L = I ω = ½ m R2 ω = ½ 2 0,12 20 => L = 0,2 kg m2 / s
Δ4.
ΣFy = m α => m g = m a => a = g = 10 m/s2 τότε υ = v0 + α t = 2 m/s + 10 m/s2 0,1s = 3 m/s
Kμεταφορική = ½ m υ2 = ½ 2 32 = 9 J
Kπεριστροφική = ½ Ι ω2 = ½ 0,01 202 = 2 J
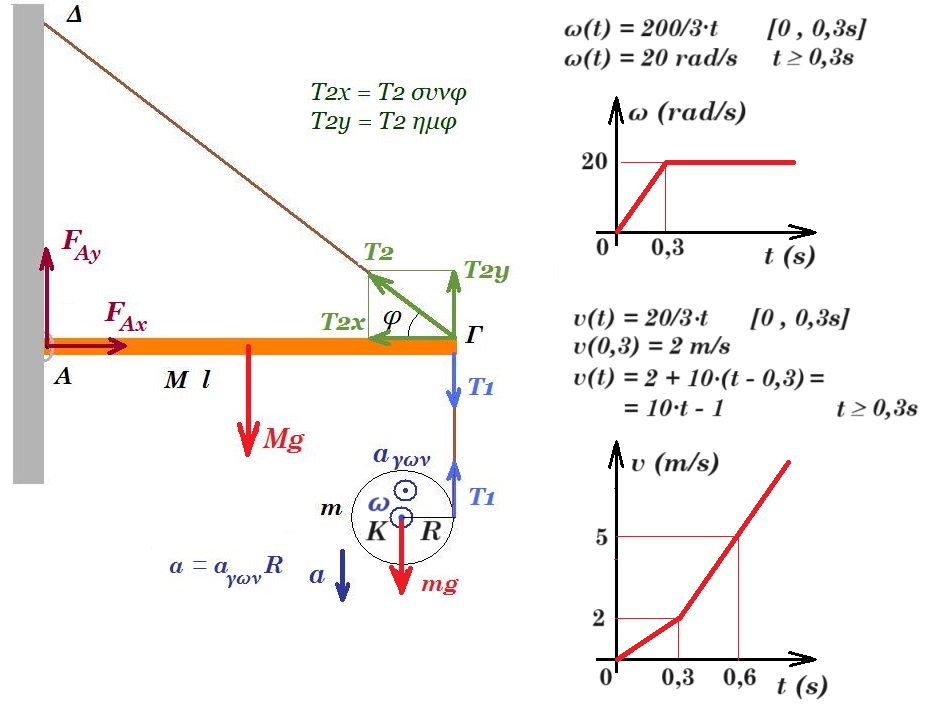
2017 τ ρ ο π ο π ο ί η σ η
Μία ομογενής άκαμπτη ράβδος ΑΓ σταθερής διατομής έχει μάζα Μ=4Kg. Η ράβδος ισορροπεί σε οριζόντια θέση και το άκρο της Α συνδέεται με άρθρωση σε κατακόρυφο τοίχο. Το άλλο άκρο Γ της ράβδου συνδέεται μέσω αβαρούς μη εκτατού νήματος ΓΔ με τον κατακόρυφο τοίχο. Το νήμα σχηματίζει με τη ράβδο γωνία φ. Γύρω από ένα λεπτό ομογενή δίσκο κέντρου Κ, μάζας m=2kg και ακτίνας R=0,1m είναι τυλιγμένο πολλές φορές ένα λεπτό μη εκτατό αβαρές νήμα. Το ελεύθερο άκρο του νήματος έχει στερεωθεί στο άκρο Γ της ράβδου ΑΓ.

Τη χρονική στιγμή t0=0 ο δίσκος αφήνεται να κινηθεί, το νήμα ξετυλίγεται χωρίς να ολισθαίνει.
Δ1. Να υπολογίσετε το μέτρο της δύναμης που δέχεται η ράβδος ΑΓ στο άκρο της Γ από το νήμα ΓΔ, όταν ο δίσκος κατέρχεται με γωνιακή επιτάχυνση 200/3 rad/s2 καθώς και την δύναμη που δέχεται η ράβδος ΑΓ στο άκρο της Α από την άρθρωση.
Τη χρονική στιγμή που το κέντρο μάζας Κ του δίσκου έχει κατέλθει κατακόρυφα κατά h1=0,3m το νήμα που συνδέει το δίσκο με τη ράβδο κόβεται.
Δ2. Να κάνετε το διάγραμμα της γωνιακής ταχύτητας του δίσκου και το διάγραμμα της ταχύτητας του κέντρου μάζας του, συναρτήσει του χρόνου από τη στιγμή t0=0 και μετά.
Δίνονται: η επιτάχυνση της βαρύτητας g = 10 m/s2 ημφ = 0,8 και συνφ = 0,6 ο άξονας περιστροφής του δίσκου παραμένει συνεχώς οριζόντιος και κινείται σε κατακόρυφη τροχιά σε όλη τη διάρκεια της κίνησης του, ο δίσκος δεν φτάνει στο έδαφος στη διάρκεια του φαινομένου.
Δ1. αγων = 200/3 rad/s2 a = αγων R = 200/3 rad/s2 0,1 m => a = 20/3 m/s2
ΣF = m a => mg - T1 = m a => 2 10 - T1 = 2 20/3 => Τ1 = 20/3 N
ροπές ως προς Α : M g l/2 + T1 l - T2 ημφ l = 0 => 4 10 /2 + 20/3 - T2 0,8 = 0 =>
=> 20 + 20/3 = T2 0,8 => T2 = 80/3 / 0,8 => T2 = 100/3 Ν
ΣFx = 0 => FAx = T2x = T2 συνφ => FAx = 100/3 0,6 = 20 Ν
ΣFy = 0 => FAy + T2y = T1 + Mg =>
=> FAy = - T2 ημφ + T1 + Mg = - 100/3 0,8 + 20/3 + 40 => FAy = 20 Ν
FA2 = FAx2 + FAy2 = 202 + 202 => FA = 20√2 Ν
Δ2.
h = ½ a t2 => 0,3 = ½ 20/3 t2 => t = 0,3 s τότε υ = α t = 20/3 0,3 = 2 m/s
ω = αγων t = 200/3 0,3 = 20 rad/s = σταθερή διότι από τη στιγμή που κόβεται το νήμα δεν δέχεται ροπή ο δίσκος Τ1 = 0
ω(t) = 200/3 t [0 , 0,3s] & ω(t) = 20 rad/s t ³ 0,3s
από 0 έως 0,3s που υπάρχει το νήμα το κέντρο μάζας του δίσκου έχει σταθερή επιτάχυνση a = 20/3 m/s2 όταν κοπεί το νήμα το κέντρο μάζας εκτελεί ελεύθερη πτώση διότι ΣFy = m α => m g = m a => a = g = 10 m/s2
v(t) = 20/3 t [0 , 0,3s] v(0,3) = 2 m/s
v(t) = v(0,3) + α (t - 0,3) = 2 + 10 (t - 0,3) = 10 t - 1 t ³ 0,3s

2019
Ομογενής, άκαμπτη και μικρού πάχους σανίδα ΑΒ μάζας Μ = 2kg και μήκους l = 4m ισορροπεί σε πλάγια θέση με τη βοήθεια υποστηρίγματος, το οποίο έχουμε στερεώσει σε λείο οριζόντιο δάπεδο. Η σανίδα ακουμπά με το άκρο της Α στο λείο δάπεδο σχηματίζοντας γωνία φ = 30° με αυτό. Η σανίδα συνδέεται με την κορυφή του υποστηρίγματος με άρθρωση σε σημείο της Γ, το οποίο απέχει από το άκρο της Β απόσταση (ΒΓ) = 1,5 m. Η σανίδα μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από το σημείο Γ (κάθετος στο επίπεδο του σχήματος).
Ομογενής κύλινδρος μάζας ΜΚ = 2 kg και ακτίνας RΚ βρίσκεται σε επαφή με τη σανίδα στο σημείο Δ, το οποίο απέχει από το Γ απόσταση (ΓΔ) = 0,2 m.
Στο μέσο της επιφάνειας του κυλίνδρου, που φέρει ένα λεπτό αυλάκι, έχουμε τυλίξει πολλές φορές λεπτό, αβαρές και μη εκτατό νήμα, στο άλλο άκρο του οποίου έχουμε δέσει σώμα Σ μικρών διαστάσεων μάζας ΜΣ = 2 kg.
Το νήμα περνάει από το αυλάκι ομογενούς τροχαλίας μάζας ΜΤ = 2 kg και ακτίνας RΤ, την οποία έχουμε στερεώσει σε ακλόνητο σημείο. Η τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από το κέντρο μάζας της και είναι κάθετος στο επίπεδο της τροχαλίας. Το τμήμα του νήματος που συνδέει τον κύλινδρο με την τροχαλία έχει διεύθυνση παράλληλη με τη σανίδα.
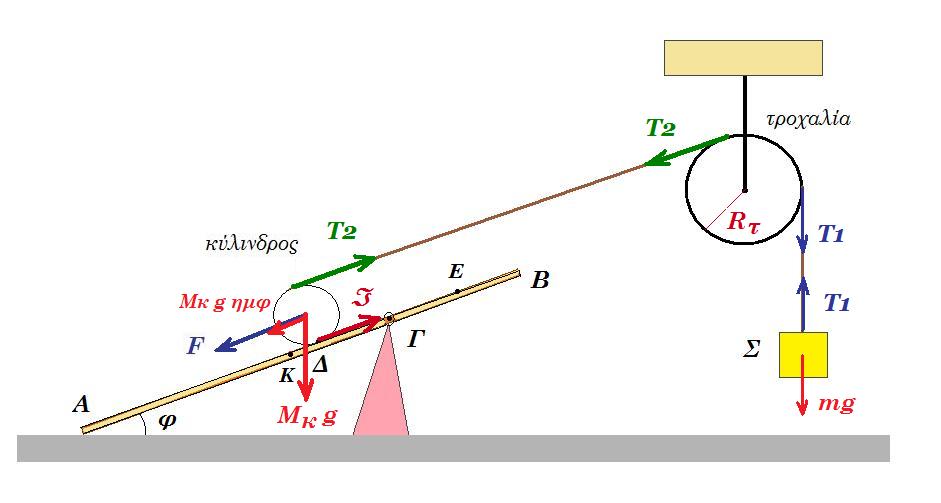
Αρχικά ασκούμε δύναμη F στο κέντρο μάζας του κυλίνδρου με διεύθυνση παράλληλη προς την διεύθυνση ΑΒ, ώστε το σύστημα κύλινδρος -τροχαλία-σώμα να ισορροπεί, όπως φαίνεται στο σχήμα .
Δ1. Να υπολογίσετε το μέτρο της δύναμης F.
Τη χρονική στιγμή t = 0 καταργούμε ακαριαία τη δύναμη και το σώμα Σ αρχίζει να κατέρχεται κατακόρυφα, ενώ ο κύλινδρος αρχίζει να ανέρχεται στη σανίδα εκτελώντας κύλιση χωρίς ολίσθηση και το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλίας.
Δ2. Να αποδείξετε ότι το μέτρο της επιτάχυνσης με την οποία κατέρχεται το σώμα Σ είναι ίσο με 4 m / s2 και να υπολογίσετε το μέτρο της επιτάχυνσης του κέντρου μάζας του κυλίνδρου.
Τη χρονική στιγμή t1 = 0,5 s κόβουμε ακαριαία το νήμα στο σημείο που εφάπτεται με τον κύλινδρο και στο σημείο πρόσδεσης με το σώμα Σ. Μετά το κόψιμο του νήματος, αυτό δεν εμποδίζει την κίνηση του κυλίνδρου και του σώματος. Ο κύλινδρος συνεχίζει την κίνησή του εκτελώντας κύλιση χωρίς ολίσθηση.
Δ3. Να υπολογίσετε τη χρονική στιγμή t2 στην οποία ο κύλινδρος σταματά στιγμιαία να κινείται πάνω στη σανίδα.
Δ4. Να υπολογίσετε το συνολικό διάστημα που διάνυσε ο κύλινδρος από τη χρονική στιγμή t = 0 έως τη χρονική στιγμή t2.
Δ5. Να δείξετε ότι κατά τη διάρκεια της ανόδου του κυλίνδρου πάνω στη σανίδα, από τη χρονική στιγμή t = 0 έως τη χρονική στιγμή t2, που ο κύλινδρος σταματά στιγμιαία, η σανίδα δεν ανατρέπεται.
Δ1. ισορροπία σώματος Σ : m g = T1 => Τ1 = 20 Ν
ισορροπία τροχαλίας : T1 Rτρ = T2 Rτρ => T1 = T2 = 20 Ν
ισορροπία κυλίνδρου : Tστ Rκ = T2 Rκ => Tστ = T2 = 20 Ν
Μκ g ημ30° + F = T2 + Tστ => 2 10 ½ + F = 20 + 20 => F = 30 Ν
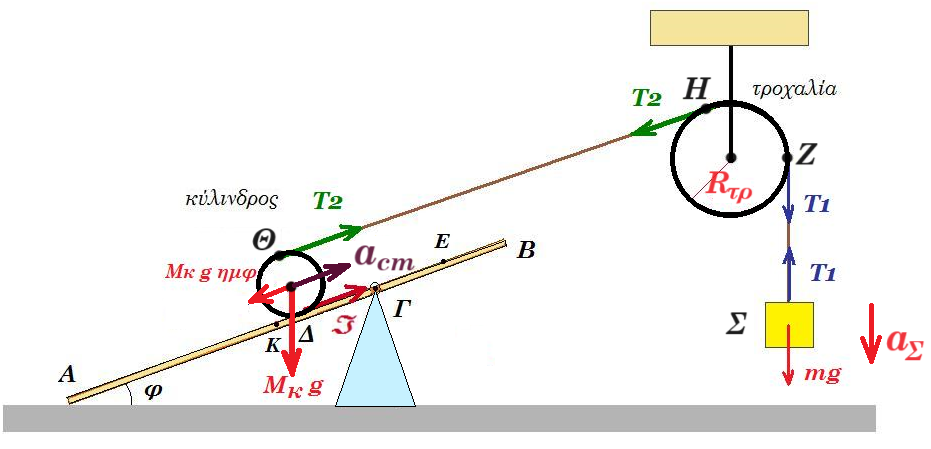
Δ2. αΣ = αγων,τρ Rτρ = aZ = aH = aΘ = 2acm
κατακόρυφη κίνηση σώματος Σ : ΣF = m aΣ => m g - T1 = m aΣ (1) αΣ = αγων,τρ Rτρ
περιστροφή τροχαλίας : T1 Rτρ - T2 Rτρ = Ιτρ αγων,τρ => T1 Rτρ - T2 Rτρ = ½ Μτρ Rτρ2 αγων,τρ =>
=> T1 - T2 = ½ Μτρ Rτρ αγων,τρ = ½ Μτρ αΣ (2)
κίνηση κυλίνδρου : Tστ Rκ + T2 Rκ = Ικ αγων,κ => Tστ Rκ + T2 Rκ = ½ Μκ Rκ2 αγων,κ =>
=> Tστ + T2 = ½ Μκ Rκ αγων,κ = ½ Μκ αcm (3)
θεωρώ την τριβή προς τα κάτω T2 - Tστ - Μκ g ημ30° = Μκ αcm (4) αΣ = 2 αcm
(3) + (4) => 2 T2 - Μκ g ημ30° = 3/2 Μκ αcm => T2 - 1/4 Μκ g = 3/4 Μκ αcm (5)
(1) + (2) + (5) => m g - T1 + T1 - T2 + T2 - 1/4 Μκ g = m aΣ + ½ Μτρ αΣ + 3/4 Μκ αcm =>
=> 20 - 1/4 20 = 2 aΣ + ½ 2 αΣ + 3/4 2 αcm => 15 = 2 aΣ + αΣ + 3/4 αΣ => αΣ = 4 m/s2 άρα αcm = 2 m/s2
(5) => T2 - 1/4 2 10 = 3/4 2 2 => T2 = 3 + 5 = 8 N η τάση νήματος Τ2 προς τα πάνω παράλληλα στο κεκλιμένο
(4) => 8 - Tστ - 2 10 0,5 = 2 2 => Τστ = 8 - 10 - 4 = - 6 Ν η τριβή προς τα πάνω παράλληλα στο κεκλιμένο
t1 = 0,5 s χκ = ½ ακ t1 = ½ 2 0,52 = 0,25 m υκ = ακ t1 = 2 0,5 = 1 m/s
κίνηση κυλίνδρου : Tστ Rκ = Ικ αγων,κ => Tστ Rκ = ½ Μκ Rκ2 αγων,κ =>
=> Tστ = ½ Μκ Rκ αγων,κ = ½ Μκ ακ (6)
- Tστ - Μκ g ημ30° = Μκ ακ (7) (6) + (7) => - Μκ g ημ30° = 3/2 Μκ ακ => ακ = - 10/3 m/s2
υκ = 1 m/s - 10/3 m/s2 t = 0 => t = 0,3 s t2 = 0,5 s + 0,3 s = 0,8 s
χ = 1 m/s 0,3 s - ½ 10/3 m/s2 0,09 s2 = 0,15 m
ο κύλινδρος έχει προχωρήσει 0,25 m + 0,15 m = 0,4 m = (ΔΕ)
(ΓΕ) = (ΔΕ) - (ΓΔ) = 0,4 - 0,2 = 0,2 m
ροπές ως προς Γ : Μ g (ΓΚ) συν30° - Μκ g (ΓΕ) συν30° = 2 10 0,5 συν30° - 2 10 0,2 συν30° > 0 υπερισχύει η ροπή του βάρους της σανίδας οπότε δεν ανατρέπεται
2019 τ ρ ο π ο π ο ί η σ η
ΘΕΜΑ Δ
Ομογενής, άκαμπτη και μικρού πάχους σανίδα ΑΒ μάζας Μ = 2kg και μήκους l = 4m ισορροπεί σε πλάγια θέση με τη βοήθεια υποστηρίγματος, το οποίο έχουμε στερεώσει σε λείο οριζόντιο δάπεδο. Η σανίδα ακουμπά με το άκρο της Α στο λείο δάπεδο σχηματίζοντας γωνία φ = 30° με αυτό. Η σανίδα συνδέεται με την κορυφή του υποστηρίγματος με άρθρωση σε σημείο της Γ, το οποίο απέχει από το άκρο της Β απόσταση (ΒΓ) = 1,5 m. Η σανίδα μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από το σημείο Γ (κάθετος στο επίπεδο του σχήματος).
Ομογενής κύλινδρος μάζας ΜΚ = 2 kg και ακτίνας RΚ βρίσκεται σε επαφή με τη σανίδα στο σημείο Δ, το οποίο απέχει από το Γ απόσταση (ΓΔ) = 0,2 m.
Στο μέσο της επιφάνειας του κυλίνδρου, που φέρει ένα λεπτό αυλάκι, έχουμε τυλίξει πολλές φορές λεπτό, αβαρές και μη εκτατό νήμα, στο άλλο άκρο του οποίου έχουμε δέσει σώμα Σ μικρών διαστάσεων μάζας ΜΣ = 2 kg.
Το νήμα περνάει από το αυλάκι ομογενούς τροχαλίας μάζας ΜΤ = 2 kg και ακτίνας RΤ, την οποία έχουμε στερεώσει σε ακλόνητο σημείο. Η τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από το κέντρο μάζας της και είναι κάθετος στο επίπεδο της τροχαλίας. Το τμήμα του νήματος που συνδέει τον κύλινδρο με την τροχαλία έχει διεύθυνση παράλληλη με τη σανίδα.
Αρχικά ασκούμε δύναμη F στο κέντρο μάζας του κυλίνδρου με διεύθυνση παράλληλη προς την διεύθυνση ΑΒ, ώστε το σύστημα κύλινδρος -τροχαλία-σώμα να ισορροπεί, όπως φαίνεται στο σχήμα.
Δ1. Να υπολογίσετε το μέτρο της δύναμης F.
Θεωρούμε ότι τα κέντρα μάζας του σώματος Σ και του κυλίνδρου βρίσκονται στο ίδιο οριζόντιο επίπεδο. Τη χρονική στιγμή t=0 καταργούμε ακαριαία τη δύναμη και το σώμα Σ αρχίζει να κατέρχεται κατακόρυφα με σταθερή επιτάχυνση 4 m/s2, ενώ ο κύλινδρος αρχίζει να ανέρχεται στη σανίδα εκτελώντας κύλιση χωρίς ολίσθηση και το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλίας.
Δ2. (α) Υπολογίσετε το μέτρο της επιτάχυνσης του κέντρου μάζας του κυλίνδρου. (β) Βρείτε την υψομετρική διαφορά των κέντρων μάζας του Σ και του κυλίνδρου συναρτήσει του χρόνου. (γ) Βρείτε την στροφορμή του σώματος Σ ενώ κατέρχεται ως προς το κέντρο της τροχαλίας συναρτήσει του χρόνου. RΤ = 0,1 m.
Τη χρονική στιγμή t1 = 0,5 s κόβουμε ακαριαία το νήμα στο σημείο που εφάπτεται με τον κύλινδρο και στο σημείο πρόσδεσης με το σώμα Σ. Μετά το κόψιμο του νήματος, αυτό δεν εμποδίζει την κίνηση του κυλίνδρου και του σώματος. Ο κύλινδρος συνεχίζει την κίνησή του εκτελώντας κύλιση χωρίς ολίσθηση με σταθερή επιβράδυνση μέτρου 10/3 m/s2.
Δ3. Να υπολογίσετε τη χρονική στιγμή t2 στην οποία ο κύλινδρος σταματά στιγμιαία να κινείται πάνω στη σανίδα.
Δ4. Να υπολογίσετε το συνολικό διάστημα που διάνυσε ο κύλινδρος από τη χρονική στιγμή t = 0 έως τη χρονική στιγμή t2.
Δ5. Να δείξετε ότι κατά τη διάρκεια της ανόδου του κυλίνδρου πάνω στη σανίδα, από τη χρονική στιγμή t = 0 έως τη χρονική στιγμή t2, που ο κύλινδρος σταματά στιγμιαία, η σανίδα δεν ανατρέπεται.
 Δ1. ισορροπία σώματος Σ : m g = T1 => Τ1 = 20 Ν
Δ1. ισορροπία σώματος Σ : m g = T1 => Τ1 = 20 Ν
ισορροπία τροχαλίας : T1 Rτρ = T2 Rτρ => T1 = T2 = 20 Ν
ισορροπία κυλίνδρου : Tστ Rκ = T2 Rκ => Tστ = T2 = 20 Ν
Μκ g ημ30° + F = T2 + Tστ => 2 10 ½ + F = 20 + 20 => F = 30 Ν

Δ2. αΣ = αγων,τρ Rτρ = aZ = aH = aΘ = 2acm => 4 m/s2 = 2 acm => acm = 2 m/s2
yΣ = ½ αΣ t2 = ½ 4 t2 = 2 t2 xκ = ½ αcm t2 = ½ 2 t2 = t2 h = xκ ημ30° = ½ t2
υψομετρική διαφορά των κέντρων μάζας = yΣ + h = 2 t2 + ½ t2 = 2,5.t2 , t > 0
L = MΣ v RΤ = MΣ aΣ t RΤ = 2 kg 4 m/s2 t 0,1 m => L(t) = 0,8.t
Δ3. Δ4. Δ5.
t1 = 0,5 s x1 = ½ αcm t12 = ½ 2 0,52 = 0,25 m υcm,1 = αcm t1 = 2 0,5 = 1 m/s
κίνηση κυλίνδρου : α'cm = - 10/3 m/s2
υcm,2 = 0 => 1 m/s - 10/3 m/s2 t = 0 => t = 0,3 s t2 = 0,5 s + 0,3 s = 0,8 s
x2 = 1 m/s 0,3 s - ½ 10/3 m/s2 0,09 s2 = 0,15 m
ο κύλινδρος έχει προχωρήσει 0,25 m + 0,15 m = 0,4 m = (ΔΕ)
(ΓΕ) = (ΔΕ) - (ΓΔ) = 0,4 - 0,2 = 0,2 m
ροπές ως προς Γ : Μ g (ΓΚ) συν30° - Μκ g (ΓΕ) συν30° = 2 10 0,5 συν30° - 2 10 0,2 συν30° > 0 υπερισχύει η ροπή του βάρους της σανίδας οπότε δεν ανατρέπεται η σανίδα
ΘΕΜΑ Γ
Ένα κατακόρυφο ιδανικό ελατήριο σταθεράς k έχει το πάνω άκρο του στερεωμένο σε ακλόνητο σημείο. Στο ελεύθερο άκρο του ελατηρίου αναρτάται σώμα Σ1 μάζας m1 = 1 kg και, όταν το σώμα ισορροπεί, η επιμήκυνση του ελατηρίου είναι ίση με Δl = 0,05 m.
Δεύτερο σώμα Σ2 μάζας m2 = 1 kg κινούμενο κατακόρυφα προς τα πάνω συγκρούεται πλαστικά με ταχύτητα μέτρου u0 με το σώμα Σ1. Η διάρκεια της κρούσης είναι αμελητέα και το συσσωμάτωμα, που προκύπτει από την κρούση, εκτελεί απλή αρμονική ταλάντωση με σταθερά επαναφοράς της ταλάντωσης D = k και φτάνει μέχρι τη θέση στην οποία το ελατήριο έχει το φυσικό του μήκος.
Γ1. Να υπολογίσετε τη σταθερά k του ελατηρίου και το πλάτος της ταλάντωσης που εκτελεί το συσσωμάτωμα. Μονάδες 6
Γ2. Να υπολογίσετε την κινητική ενέργεια του σώματος Σ2 πριν την κρούση. Μονάδες 7
Γ3. Να υπολογίσετε την μεταβολή της ορμής του σώματος Σ2 κατά την κρούση. Μονάδες 6
Γ4. Αν t0 = 0 η χρονική στιγμή της κρούσης, να γράψετε τη σχέση που δίνει την απομάκρυνση του συσσωματώματος από την θέση ισορροπίας του σε συνάρτηση με τον χρόνο. Μονάδες 6
Να θεωρήσετε :
θετική κατεύθυνση την κατεύθυνση κίνησης του συσσωματώματος αμέσως μετά την κρούση ότι κατά την κρούση δεν έχουμε απώλεια μάζας ότι η αντίσταση του αέρα θεωρείται αμελητέα για όλα τα σώματα.
η επιτάχυνση της βαρύτητας g = 10 m/s2.
ισορροπία Σ1 : k Δl = m1 g => k 0,05 = 1 10 => k = 10/0,05 = 200 N/m
ισορροπία Σ1,2 : k Δl = m1,2 g => 200 Δl' = 2 10 => Δl' = 0,1 m
πλαστική κρούση διατήρηση ορμής : m2 v0 = (m1 + m2) u => 1 v0 = 2 u => u = v0 / 2
Α.Α.Τ. συσσωματώματος : ½ k (Δl' - Δl)2 + ½ (m1 + m2) u2 = ½ k A2 (1)
επειδή το συσσωμάτωμα μετά την κρούση φθάνει στη θέση όπου το φυσικό μήκος του ελατηρίου Α = Δl' = 0,1 m
(1) => ½ k (Δl' - Δl)2 + ½ (m1 + m2) u2 = ½ k A2 => 200 0,052 + 2 u2 = 200 0,12 =>
=> 0,5 + 2 u2 = 2 => u2 = 3/4 => u = √3/2 m/s άρα v0 = √3 m/s
Δp2 = m2 u - m2 v0 = 1 √3/2 - 1 √3 = - √3/2 kg m/s
k = (m1 + m2) ω'2 => 200 = 2 ω'2 => ω' = 10 rad/s
x(t) = 0,1 ημ(10t + θ) x(0) = ημ(θ) = +0,05 m
v(t) = 1 συν(10t + θ) v(0) = 1 συν(θ) = u = +√3/2 m/s θ = π/6
x(t) = 0,1 ημ(10t + π/6) v(t) = 1 συν(10t + π/6) α(t) = - 10 ημ(10t + π/6)
2022 θέμα Γ
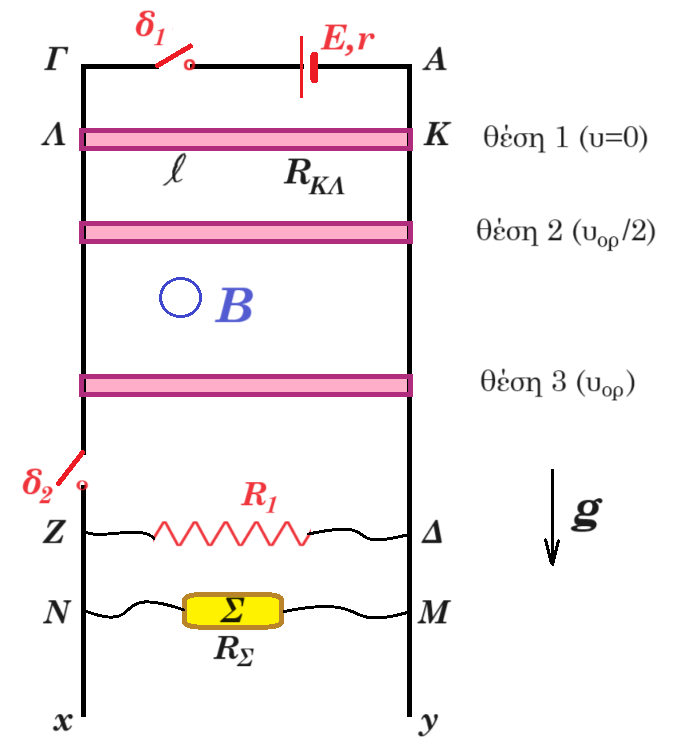
Οι μεγάλου μήκους, κατακόρυφοι, μεταλλικοί αγωγοί Αx και Γy απέχουν μεταξύ τους σταθερή απόσταση l = 1 m και έχουν αμελητέα ωμική αντίσταση. Στα άκρα Α, Γ συνδέεται πηγή ηλεκτρεγερτικής δύναμης Ε = 9 V και εσωτερικής αντίστασης r = 1 Ω.
Αγωγός ΚΛ μήκους l = 1 m, μάζας m = 0,3 kg και ωμικής αντίστασης RΚΛ = 2 Ω έχει τα άκρα του Κ, Λ πάνω στους κατακόρυφους αγωγούς Αx και Γy, είναι κάθετος σε αυτούς και είναι δυνατόν να ολισθαίνει κατά μήκος των αγωγών χωρίς τριβές.
Η όλη διάταξη βρίσκεται σε περιοχή που υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης B, του οποίου οι δυναμικές γραμμές είναι κάθετες στο επίπεδο του σχήματος.
Αρχικά ο διακόπτης δ1 είναι κλειστός, ο διακόπτης δ2 είναι ανοικτός και ο αγωγός ΚΛ είναι ακίνητος στη θέση 1.
Γ1. Να υπολογίσετε το μέτρο Β της έντασης του μαγνητικού πεδίου (μονάδες 3) και να προσδιορίσετε την κατεύθυνσή της. (μονάδα 1) Μονάδες 4
Στο κάτω μέρος της διάταξης, μεταξύ των σημείων Ζ και Δ, είναι συνδεδεμένος αντιστάτης με ωμική αντίσταση R1 = 3 Ω και στα σημεία Μ, Ν είναι συνδεδεμένη θερμική συσκευή Σ ωμικής αντίστασης RΣ, η οποία όταν στα άκρα της Μ, Ν έχει τάση ίση με 6 V λειτουργεί κανονικά αποδίδοντας θερμική ισχύ 6 W.
Ανοίγουμε τον διακόπτη δ1, κλείνοντας ταυτόχρονα τον διακόπτη δ2 και ο αγωγός ΚΛ αρχίζει να κατέρχεται παραμένοντας συνεχώς οριζόντιος χωρίς τα άκρα του Κ, Λ να χάνουν την επαφή με τους αγωγούς Αx και Γy.
Γ2. Έστω ότι ο αγωγός ΚΛ έχει αποκτήσει οριακή ταχύτητα uορ στη θέση 3.
Να δικαιολογήσετε το είδος της κίνησης που εκτελεί ο αγωγός ΚΛ από τη θέση 1 έως τη θέση 3 (μονάδες 3) και να υπολογίσετε τη σταθερή οριακή ταχύτητα uορ. (μονάδες 6) Μονάδες 9
Γ3. Να υπολογίσετε τον ρυθμό μεταβολής της ορμής του αγωγού στη θέση 2, στην οποία η ταχύτητά του είναι ίση με
uορ/2. Μονάδες 6
Γ4. Όταν ο αγωγός έχει αποκτήσει την οριακή του ταχύτητα, να εξετάσετε αν η θερμική συσκευή Σ λειτουργεί κανονικά. Μονάδες 6
• Δίνεται η επιτάχυνση της βαρύτητας: g = 10 m/s2
• Η αντίσταση του αέρα θεωρείται αμελητέα.
• Το σχήμα δεν είναι υπό κλίμακα.
Γ1. ο δ2 ανοικτός ο δ1 κλειστός ο αγωγός ΚΛ διαρέεται από ρεύμα από το Λ προς το Κ (δεξιά) i = E / (r + RΚΛ) = 9 / (1 + 2) = 3 Α
ο αγωγός δέχεται δύναμη Laplace FL = B l i
ο αγωγός είναι ακίνητος ΣF = 0 => mg - FL = 0 => mg = B l i => B = mg / il = 3 / 3 = 1 Tesla
η δύναμη Laplace είναι αντίθετη του βάρους του αγωγού (προς τα πάνω) η ένταση Β είναι προς τα μέσα
ωμική αντίσταση συσκευής : RΣ = V2 / P = 62 / 6 = 6 Ω
Γ2. ο δ1 ανοίγει ο δ2 κλείνει
η συσκευή συνδέεται παράλληλα με την R1 R1,Σ = 6 3 / (6 + 3) = 2 Ω
ο αγωγός κατέρχεται μέσα στο μαγνητικό πεδίο τα ηλακτρ'ονια του δέχονται δύναμη Lorentz και κινούνται προς το άκρο Λ που φορτίζεται αρνητικά και το Κ φορτίζεται θετικά αναπτύσσεται επαγωγική τάση
κλειστό κύκλωμα Εεπαγ = i ( RΚΛ + R1,Σ ) => B l v = i ( RΚΛ + R1,Σ ) => 1 1 v = i ( 2 + 2 ) => v = 4i i = v/4
ΣF = m a => mg - B l i = m a => 3 - v/4 = 0,3 a (1) καθώς η ράβδος κατέρχεται η ταχύτητά της αυξάνεται οπότε το μέτρο της επιτάχυνσης μειώνεται και κάποια στιγμή μηδενίζεται οπότε η (1) => v = 12 m/s οριακή ταχύτητα αμέσως μετά ( α = 0 ) η ράβδος ΚΛ κατέρχεται με σταθερή ταχύτητα vορ = 12 m/s
Γ3. θέση 2 : vορ/2 = 6 m/s i = v/4 = 6/4 = 1,5 A
ΣF = m a => ΣF = mg - B l i = m a => ΣF = 3 - 1 1 1,5 = 0,3 a => ΣF = dp/dt = 1,5 N
a = 1,5 / 0,3 = 5 m/s2
Γ4. θέση 3 και μετά ........ i = v/4 = 12/4 = 3 A
VΚΛ = Εεπαγ - i RΚΛ = B l vor - i RΚΛ = 1 1 12 - 3 2 = 6 Volt
στα άκρα της συσκευής επικρατεί τάση 6 Volt άρα λειτουργεί κανονικά
η συσκευή διαρρέεται από iΣ = VΚΛ / RΣ = 6 / 6 = 1 Α άρα λειτουργεί κανονικά
η αντίσταση R1 διαρρέεται από i1 = VΚΛ / R1 = 6 / 3 = 2 Α
2023
B1. Δφ / Δx = (0 - 4π) / 4 = - π rad/m
t = 2s φ(x) = 4π - πx = 2π 2s/T - 2πx/2m = 2π t/T - 2π x/λ
t = 2s Τ = 1s λ = 2m v = λ/T = 2 m/s
t = 2,5s φ(x) = 2π t/T - 2π x/λ = 2π 2,5/1 - 2π x/2 = 5π - πx
5m = 2m + 2m + 1m = λ + λ + λ/2 για κάθε μήκος κύματος λ υπάρχουν 2 σημεία σε ακραία θέση και για λ/2 υπάρχει 1 σημείο σε ακραία θέση συναλικά σε απόσταση 5m = 2,5 λ υπάρχουν 2 + 2 + 1 = 5 σημεία σε ακραία θέση
y = A ημ2π(t/T - x/λ) = A ημ2π(t/1 - x/2) = A ημ2π(t - x/2)
t = 2 s y = A ημ2π(2 - x/2) = A ημ(4π - x)
t = 2,5 s y = A ημ2π(2,5 - x/2) = A ημ(5π - x)
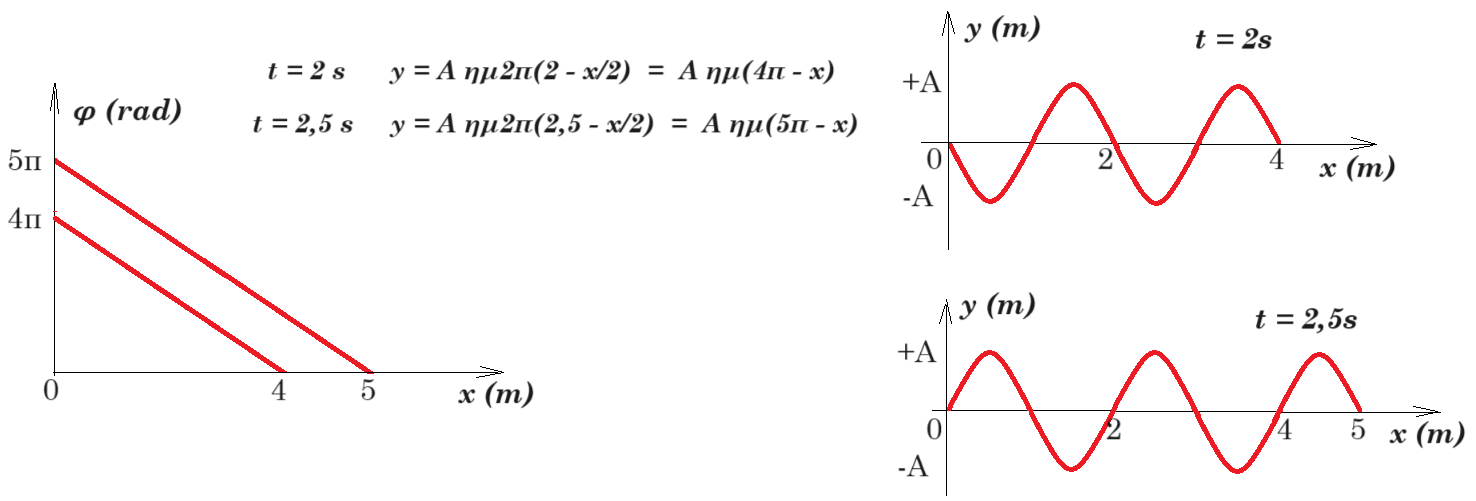
B2. h f1 = φ έργο εξαγωγής του μετάλλου της καθόδου
e V + h f2 = Ke + φ επειδή τα ηλεκτρόνια μόλις που φθάνουν στην άνοδο Ke = 0 και η τάση μεταξύ ανόδου καθόδου είναι αρνητική (τάση αποκοπής) οπότε e V0 + h f2 = φ => e V0 + h 3f1 = h f1 => e V0 = - h 2f1 => V0 = - 2⋅h⋅f1 /e τάση αποκοπής (αρνητική)
B3. FE = FB => E q = B1 q v => v = E / B1
R1 = m1 v / q B2 R2 = m2 v / q B2 d = 2R2 - 2R1 = 2(m2 - m1) v / qB2 = 2Δm v / qB2
Δm = m2 - m1 = d q B2 / 2v = d⋅ q⋅ B2⋅ B1 / 2⋅ E
Γ. πηνίο L = 0,5 H ράβδος ΖΗ l = 1 m m = 0,5 kg R = 1 Ω Β = 1 Τ
στο μέσον της ράβδου ασκείται κατακόρυφη προς τα πάνω δύναμη F οπότε η ράβδος κινείται προς τα πάνω παραμένοντας συνεχώς οριζόντια
λόγω της κίνησης της ράβδου ΖΗ ο βρόχος ΖΑΓΗΖ διαρρέεται από ρεύμα εντάσεως i = 2⋅ t (S.I.)
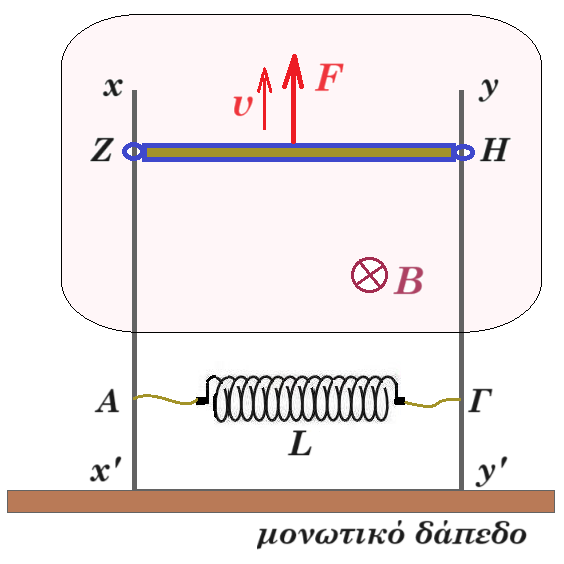
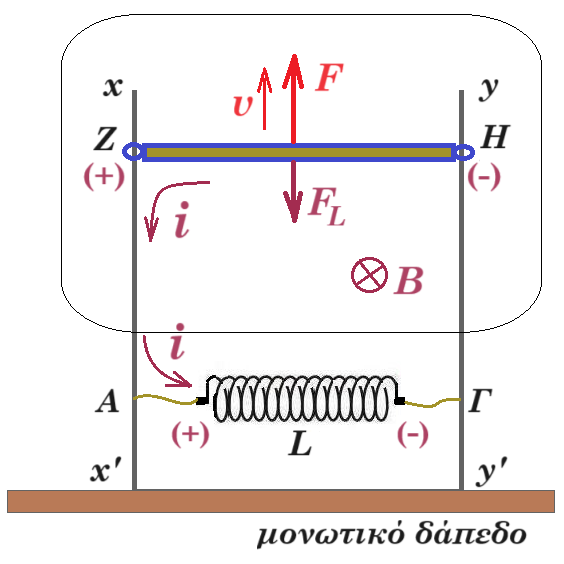
τα ηλεκτρόνια της ράβδου ΖΗ δέχονται δύναμη Lorentz κινούνται προς το άκρο Η που φορτίζεται αρνητικά (το άκρο Ζ φορτίζεται θετικά)
στα άκρα της ράβδου ΖΗ αναπτύσσεται επαγωγική τάση Εεπ = B l v ο βρόχος ΖΑΓΗΖ διαρρέεται από ρεύμα εντάσεως i = 2⋅ t di/dt = 2 A/s
φορτίο i = dq/dt => dq = i dt = 2⋅ t dt => q(t) = t2 q(0) = 0 q(2) = 4 Cb
το πηνίο αντιδρά στην διέλευση του ρεύματος για αυτό στα άκρα το εμφανίζεται τάση αυτεπαγωγής ΕΑΥΤ = - L⋅ di/dt = - 0,5 2 = - 1 Volt
νόμος του Ohm για κλειστό κύκλωμα : B l v - L⋅ di/dt = i R => 1 1 v - 0,5⋅ 2 = 2⋅ t 1 => v - 1 = 2⋅ t => v(t) = 2⋅ t + 1 a = dv/dt = 2 m/s2
η ράβδος δέχεται δύναμη Laplace αντίρροπη της F : FL = B l i = 1 1 2⋅ t => FL = 2⋅ t
ΣF = m a => F - FL - mg = m a => F - 2⋅ t - 0,5 10 = 0,5 2 => F(t) = 2⋅ t + 6
PF = F v = (2⋅ t + 6) (2⋅ t + 1) t = 2s PF = 50 J/s
U = 0,5 L i2 = 0,5 0,5 (2⋅ t)2 => U(t) = t2 U(2) = 4 J
dU/dt = L i di/dt = 0,5 2⋅ t 2 => dU(t) / dt = 2⋅ t t = 2s dU/dt = 4 J/s
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
επαναληπτικές ΣΕΠ 2024
Β2. Ένα φωτόνιο μήκους κύματος λ προσπίπτει και σκεδάζεται από πρακτικά ακίνητο ελεύθερο ηλεκτρόνιο. Η γωνία σκέδασης του φωτονίου είναι φ = 60°. Η διεύθυνση στην οποία κινείται το ηλεκτρόνιο (μετά τη σκέδαση) σχηματίζει γωνία θ = 30° με τη διεύθυνση του προσπίπτοντος φωτονίου.
Αν γνωρίζετε ότι η σκέδαση πραγματοποιείται στο κενό, m είναι η μάζα του ηλεκτρονίου, c η ταχύτητα του φωτός στο κενό και h η σταθερά του Planck, τότε για το μήκος κύματος λ του προσπίπτοντος φωτονίου ισχύει ότι :
α) λ = h/2mc β) λ = h/mc γ) λ = 2h/mc
λ' - λ = h/mc (1 - συν60°) => λ' = λ + h/2mc (1)
διατήρηση ορμής :
άξονας y : h/λ' ημ60° = pe ημ30°
άξονας x : h/λ = h/λ' συν60° + pe συν30° => h/λ - h/2λ' = pe συν30°
h/λ' ημ60° / ( h/λ - h/2λ') = pe ημ30° / pe συν30°
h/λ' 3½/2 / ( h/λ - h/2λ') = 1/3½
3 h/λ' = 2 ( h/λ - h/2λ')
3 h/λ' = 2 h/λ - h/λ'
4 h/λ' = 2 h/λ => 2 λ = λ' (2) (1) , (2) => 2λ = λ + h/2mc => λ = h/2mc
B3. WF = WFL = FL a = B l i a = Bla Blv/R = B2 l2 a v / R = B2 a3 v / R
ΘΕΜΑ Γ
Στον φασματογράφο μάζας του παρακάτω σχήματος, μονοσθενή αρνητικά ιόντα χλωρίου ( Cl- ) από μία πηγή, περνούν μέσα από τις σχισμές S1 και S2, σχηματίζοντας μια λεπτή δέσμη. Η δέσμη εισέρχεται σε επιλογέα ταχυτήτων, δηλαδή σε περιοχή όπου συνυπάρχουν ομογενές μαγνητικό πεδίο έντασης Β1 μέτρου 4 ∙ 10-2 Τ και ομογενές ηλεκτρικό πεδίο έντασης Ε μέτρου 2 ∙ 103 V/m, κάθετα μεταξύ τους και κάθετα στη διεύθυνση της δέσμης. Η φορά των μαγνητικών γραμμών είναι από τον αναγνώστη προς τη σελίδα.
Μερικά από τα ιόντα που δεν εκτρέπονται και συνεχίζουν την πορεία τους, διέρχονται από λεπτή οπή διαφράγματος, του οποίου η επιφάνεια είναι κάθετη στη διεύθυνση της δέσμης. Αμέσως μετά τη δίοδό τους από την οπή εισέρχονται
σε ομογενές μαγνητικό πεδίο έντασης Β2 μέτρου 0,1 Τ. Η φορά των μαγνητικών γραμμών είναι από τον αναγνώστη προς τη σελίδα.
Τα ιόντα στη συνέχεια, εκτελώντας καμπυλόγραμμη κίνηση, δημιουργούν πάνω σε φωτογραφική πλάκα δύο στίγματα στα σημεία Γ και Δ που απέχουν μεταξύ τους απόσταση (ΓΔ) = 0,02 m.
Γ1. Να αιτιολογήσετε γιατί μερικά από τα ιόντα χλωρίου δεν εκτρέπονται κατά την κίνησή τους μέσα στον επιλογέα ταχυτήτων. Μονάδες 5
Γ2. Να υπολογίσετε το μέτρο της ταχύτητας των ιόντων χλωρίου που δεν εκτρέπονται κατά την κίνησή τους μέσα στον επιλογέα ταχυτήτων. Μονάδες 6
Γ3. Τα ιόντα χλωρίου δημιουργούν δύο στίγματα πάνω στη φωτογραφική πλάκα, γιατί το χλώριο (Cl) έχει δύο ισότοπα με μάζες m1 και m2. Αν m1 > m2, να αιτιολογήσετε σε ποια θέση (Γ ή Δ) δημιουργούν στίγμα τα ισότοπα χλωρίου με τη μεγαλύτερη μάζα. Μονάδες 6
Γ4. Να αποδείξετε ότι το ισότοπο του χλωρίου μάζας m1 έχει δύο νετρόνια περισσότερα από το ισότοπο μάζας m2. Μονάδες 8
E = v B1 => 2 ∙ 103 = v 4 ∙ 10-2 => v = 5 ∙ 104 m/s
d = 2 (R1 - R2) => d = 2 ( m1 v / qB2 - m2 v / qB2 ) =>
=> 0,02 = 2 ( m1 5 ∙ 104 / 1,6 ∙ 10-19 0,1 - m2 5 ∙ 104 / 1,6 ∙ 10-19 0,1 ) =>
=> 0,01 = ( m1 - m2 ) 5 ∙ 104 / 1,6 ∙ 10-19 0,1 => m1 - m2 = 16/5 ∙ 10-27 = 3,2 ∙ 10-27 kg = 2 mn
ΘΕΜΑ Δ
Η λεπτή ομογενής και ισοπαχής ράβδος ΑΔ, μάζας Μρ = 4 kg και μήκους L του παρακάτω σχήματος ισορροπεί οριζόντια. Το άκρο της Α έχει συνδεθεί με άρθρωση σε κατακόρυφο τοίχο. Στο μέσον της Γ έχει δεθεί το ένα άκρο αβαρούς και μη εκτατού νήματος, το άλλο άκρο του οποίου έχει στηριχθεί στον κατακόρυφο τοίχο στο σημείο Β. Το νήμα σχηματίζει γωνία φ = 30° με τη διεύθυνση της ράβδου.
Σε σημείο Ζ της ράβδου, το οποίο απέχει από το άκρο της Δ απόσταση (ΖΔ) = L / 4, έχει στερεωθεί το κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 Ν/m. Στο πάνω άκρο του ελατηρίου έχει δεθεί σώμα Σ1 μικρών
διαστάσεων, μάζας m1 = 0,6 kg. Πάνω στο σώμα Σ1 έχει τοποθετηθεί σώμα Σ2 μικρών διαστάσεων, μάζας m2 = 0,4 kg. Ασκώντας σταθερή κατακόρυφη δύναμη F με φορά προς τα κάτω στο σώμα Σ2, το σύστημα των δύο σωμάτων ισορροπεί με το ελατήριο να έχει συμπιεστεί κατά Δ l = 0,3 m.
Ως θετική φορά να θεωρήσετε τη φορά προς τα πάνω. Σε όλη τη διάρκεια του φαινομένου το νήμα δεν χαλαρώνει και η ράβδος παραμένει οριζόντια.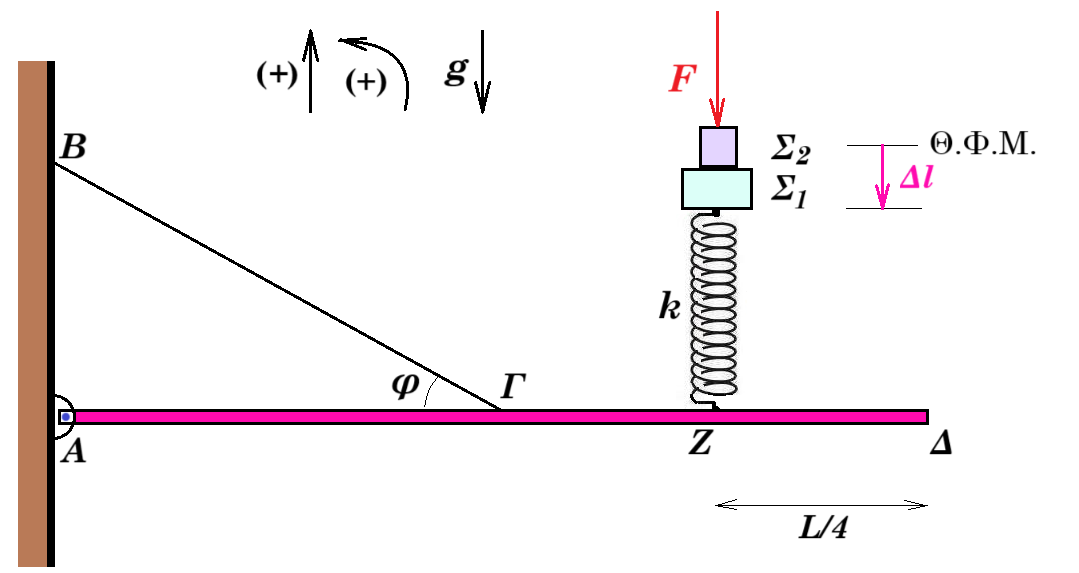
Δ1. Να υπολογίσετε το μέτρο της δύναμης F. Μονάδες 4
Τη χρονική στιγμή t0 = 0, καταργούμε τη δύναμη F. Το σύστημα των δύο σωμάτων Σ1 και Σ2 αρχίζει να εκτελεί απλή αρμονική ταλάντωση με σταθερά επαναφοράς D = k.
Δ2. Να βρείτε σε ποια θέση κατά την ταλάντωση του συστήματος των δύο σωμάτων το σώμα Σ2 θα αποσπαστεί από το σώμα Σ1. Μονάδες 6
Δ3. Τη χρονική στιγμή t1, που το σώμα Σ2 αποσπάται από το σώμα Σ1, να υπολογίσετε το μέτρο της δύναμης που ασκεί το νήμα στο μέσον Γ της ράβδου. Μονάδες 6
Τη χρονική στιγμή t1, που το σώμα Σ2 αποσπάται από το σώμα Σ1, το σώμα Σ2 συνεχίζει να κινείται κατακόρυφα προς τα πάνω, ενώ το σώμα Σ1 αρχίζει να εκτελεί απλή αρμονική ταλάντωση με σταθερά επαναφοράς D = k.
Δ4. Να υπολογίσετε την κατακόρυφη απόσταση που διανύει το σώμα Σ2 από τη χρονική στιγμή t1 μέχρι να σταματήσει στιγμιαία. Μονάδες 4
Όταν το Σ2 φτάσει στο ανώτερο ύψος του, απομακρύνεται.
Δ5. Να υπολογίσετε την ενέργεια ταλάντωσης του σώματος Σ1. Μονάδες 5
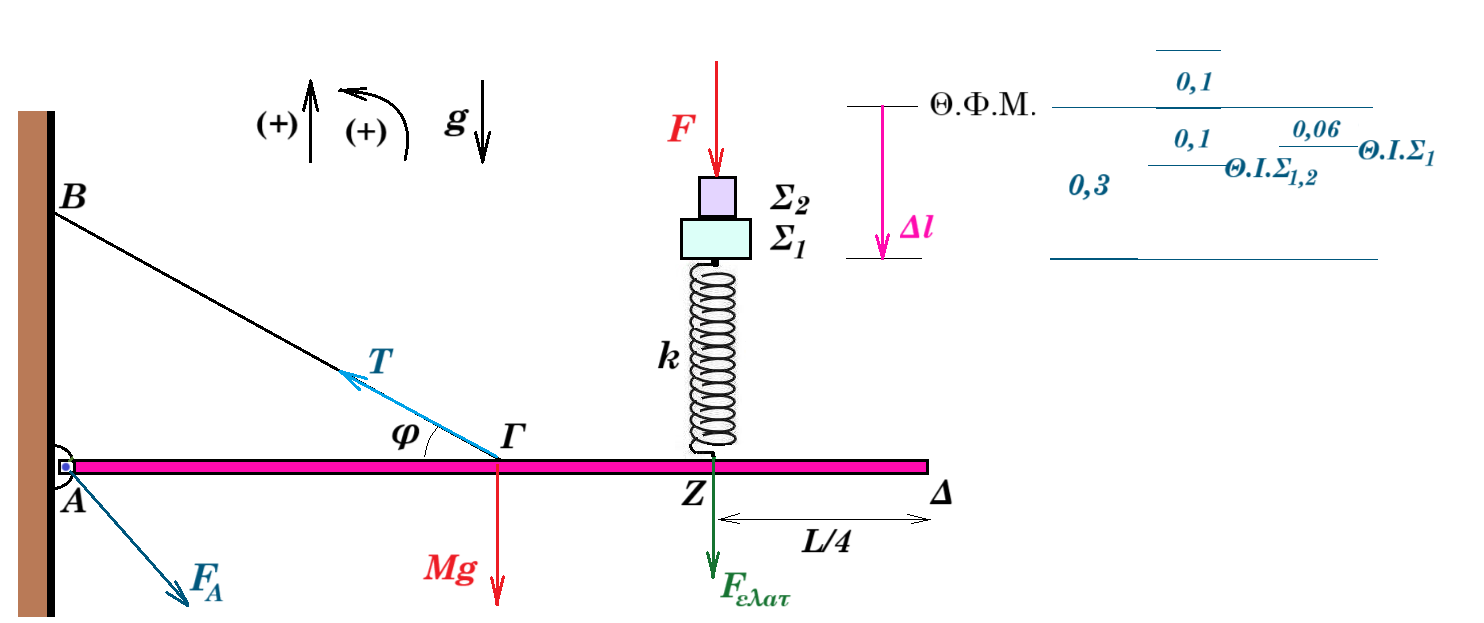
Δ1. ισορροπία Σ1,Σ2 : F + (m1 + m2) g = Fελατ = k Δl => F + 1 10 = 100 0,3 => F = 20 N
ισορροπία ράβδου : Στ(Α) = 0 => T ημ30° l/2 - Mg l/2 - Fελατ 3l/4 = 0 =>
=> T ½ 1/2 - 4 10 1/2 - 30 3/4 = 0 =>(*4) Τ = 8 10 + 90 = 170 Ν
Στ(Γ) = 0 => FΑ,y l/2 - Fελατ l/4 = 0 => FΑ,y 1/2 = 30 1/4 => FΑ,y = 15 N
FA,x = Tx = T συν30° = 170 √3/2 = 85 √3 Ν
FA2 = 152 + 852 3 = .........
Στ(Z) = 0 => - T ημ30° l/4 + Mg l/4 + FA,y 3l/4 = 0 =>
=> - 170 1/2 1/4 + 4 10 1/4 + FA,y 3/4 = 0 =>
=> FA,y 3 = 85 - 40 => FA,y = 45 / 3 = 15
ισορροπία Σ1,2 : (m1 + m2) g = k x1,2 => 1 10 = 100 x1,2 => x1,2 = 0,1 m συσπείρωση
k = (m1 + m2) ω1,22 => 100 = 1 ω1,22 => ω1,2 = 10 rad/s
ισορροπία Σ1 : m1 g = k x1 => 0,6 10 = 100 x1 => x1 = 0,06 m συσπείρωση
k = m1 ω12 => 100 = 0,6 ω12 => ω1 = 12,9 rad/s
το Σ1,2 ταλαντώνεται με πλάτος A = 0,3 m - 0,1 m = 0,2 m και κυκλική συχνότητα ω1,2 = 10 rad/s
x(t) = 0,2 ημ(10.t + 3π/2) v(t) = 2 συν(10.t + 3π/2) α(t) = - 20 ημ(10.t + 3π/2)
ΣF = (m1 + m2) a = - 20 ημ(10.t + 3π/2) = - 100.x = - k x -0,2m £ x £ +0,2m
ΣF = - (m1 + m2) g + Fελατ => - 100.x = - 10 + Fελατ => Fελατ = 10 - 100.x = - 100 (x - 0,1)
Δ2. για το Σ2 : ΣF(2) = m2 a = 0,4 [ - 20 ημ(10.t + 3π/2) ] = - 8 ημ(10.t + 3π/2)
ΣF(2) = Ν - m2 g => - 8 ημ(10.t + 3π/2) = N - 0,4 10 => N = 4 - 8 ημ(10.t + 3π/2) =>
=> Ν = 4 - 8 x/0,2 = 4 - 40.x
το Σ2 χάνει την επαφή του με το Σ1 όταν Ν = 0 => 4 - 40.x = 0 => x = 0,1 m
εκείνη τη στιγμή το ελατήριο έχει το φυσικό του μήκος
τα σώματα έχουν ταχύτητα : v = 2 συν(10.t + 3π/2) επειδή x = 0,1 m = 0,2 ημ(10.t + 3π/2) => ημ(10.t + 3π/2) = 0,5 => συν(10.t + 3π/2) = + √3/2 διότι τα σώματα κινούνται προς τα πάνω (θετικά) οπότε v = 2 συν(10.t + 3π/2) = 2 √3/2 = + √3 m/s
Δ4. το Σ2 εκτελεί κατακόρυφη βολή προς τα πάνω σταματά στιγμιαία v = v0 - g t => 0 = √3 - 10 t => t = 0,1 √3 s διανύει απόσταση y = v0 t - 0,5 g t2 = √3 0,1√3 - 0,5 10 0,03 = 0,3 - 0,15 = 0,15 m
Δ3. ισορροπία ράβδου : Στ(Α) = 0 => T ημ30° l/2 - Mg l/2 - Fελατ 3l/4 = 0 =>
=> T ½ 1/2 - 4 10 1/2 - 0 = 0 => Τ = 80 Ν
Δ5. μετά την απομάκρυνση του Σ2 το Σ1 θα εκτελέσει ΑΑΤ
ισορροπία Σ1 : m1 g = k x1 => 0,6 10 = 100 x1 => x1 = 0,06 m συσπείρωση
k = m1 ω12 => 100 = 0,6 ω12 => ω1 = 10 √(5/3) = 12,9 rad/s
το Σ1 βρίσκεται 0,06 m πάνω από τη Θέση Ισορροπίας του και έχει ταχύτητα + √3 m/s
ενέργεια ταλάντωσης : ½ 100 0,062 + ½ 0,6 (√3)2 = ½ 100 0,0036 + ½ 0,6 3 = 0,18 + 0,9 = 1,08 J = ½ 100 Α2 => Α2 = 0,0216 = 0,0036 6 => Α = 0,06 √6 m » 0,147 m πλάτος ταλάντωσης του Σ1
x = 0,06 √6 ημ( 10 √(5/3).t + θ )
t = 0 x = 0,06 m = 0,06 √6 ημ( θ ) => √6 ημ( θ ) = 1 => ημθ = 1/√6
επαναληπτικές ΣΕΠ 2023
ΘΕΜΑ Γ
Η μεταλλική ράβδος ΟΑ περιστρέφεται κατά τη φορά περιστροφής των δεικτών του ρολογιού με σταθερή γωνιακή ταχύτητα ω μέτρου ω = 2 rad/s σε οριζόντιο επίπεδο γύρω από κατακόρυφο άξονα που διέρχεται από το άκρο της Ο. Κατά τη διάρκεια της περιστροφής ο αγωγός εφάπτεται σε κυκλικούς αγώγιμους οδηγούς ακτίνων (ΟΑ) = ℓ1 = 0,4 m και (ΟΓ) = ℓ2 = 0,2 m. Οι κυκλικοί οδηγοί, τα σύρματα σύνδεσης και ο αγωγός ΟΑ έχουν αμελητέα ωμική αντίσταση.
Ο διακόπτης (δ) αρχικά είναι ανοιχτός. Το μέτρο της έντασης του ομογενούς μαγνητικού πεδίου είναι ίσο με Β = 1 Τ και η φορά της από τον αναγνώστη προς τη σελίδα.
Γ1. Να αποδείξετε ότι η τάση VΑΓ μεταξύ των σημείων επαφής Α, Γ του περιστρεφόμενου αγωγού με τους κυκλικούς οδηγούς είναι ίση με VΑΓ = 0,12 V. Μονάδες 6
Μεταξύ των άκρων Ζ και Η των κυκλικών οδηγών, παρεμβάλλεται το κύκλωμα του παραπάνω σχήματος, το οποίο βρίσκεται έξω από το ομογενές μαγνητικό πεδίο.
Το κύκλωμα περιλαμβάνει πηνίο που έχει συντελεστή αυτεπαγωγής L = 0,2 Η και ωμική αντίσταση R1 = 1,2 Ω. Ο αντιστάτης R2 έχει ωμική αντίσταση R2 = 0,6 Ω.
Γ2. Κάποια στιγμή κλείνουμε τον διακόπτη (δ). Να σχεδιάσετε και να αιτιολογήσετε την πολικότητα της ΗΕΔ από αυτεπαγωγή στο πηνίο. (μονάδες 2) Να υπολογίσετε το ρυθμό μεταβολής της έντασης του ρεύματος στο πηνίο αμέσως μετά το κλείσιμο του διακόπτη (δ). (μονάδες 4) Μονάδες 6
Γ3. Μετά από λίγο και ενώ ο αγωγός ΟΑ συνεχίζει να περιστρέφεται τα ρεύματα στο κύκλωμα σταθεροποιούνται. Υπολογίστε τις σταθεροποιημένες τιμές των εντάσεων των ρευμάτων.
Μονάδες 6
Γ4. Κάποια στιγμή ανοίγουμε τον διακόπτη (δ). Να σχεδιάσετε και να αιτιολογήσετε την πολικότητα της ΗΕΔ από αυτεπαγωγή στο πηνίο. (μονάδες 2) Να υπολογίσετε το ρυθμό μεταβολής της έντασης του ρεύματος στο πηνίο αμέσως μετά το άνοιγμα του διακόπτη (δ); (μονάδες 2) Να υπολογίσετε το ποσό της θερμότητας που μεταφέρεται στο περιβάλλον
λόγω φαινομένου Joule στους αντιστάτες, από τη στιγμή που ανοίγει ο διακόπτης (δ) και μέχρι το ρεύμα να μηδενιστεί. (μονάδες 3) Μονάδες 7
Θεωρείστε ότι κατά τη διάρκεια της περιστροφικής κίνησης, ο αγωγός ΟΑ βρίσκεται διαρκώς μέσα στο ομογενές μαγνητικό πεδίο και για όσο χρονικό διάστημα μελετάμε το φαινόμενο δεν φτάνει στην περιοχή του κυκλώματος.
Το σχήμα δεν είναι υπό κλίμακα.
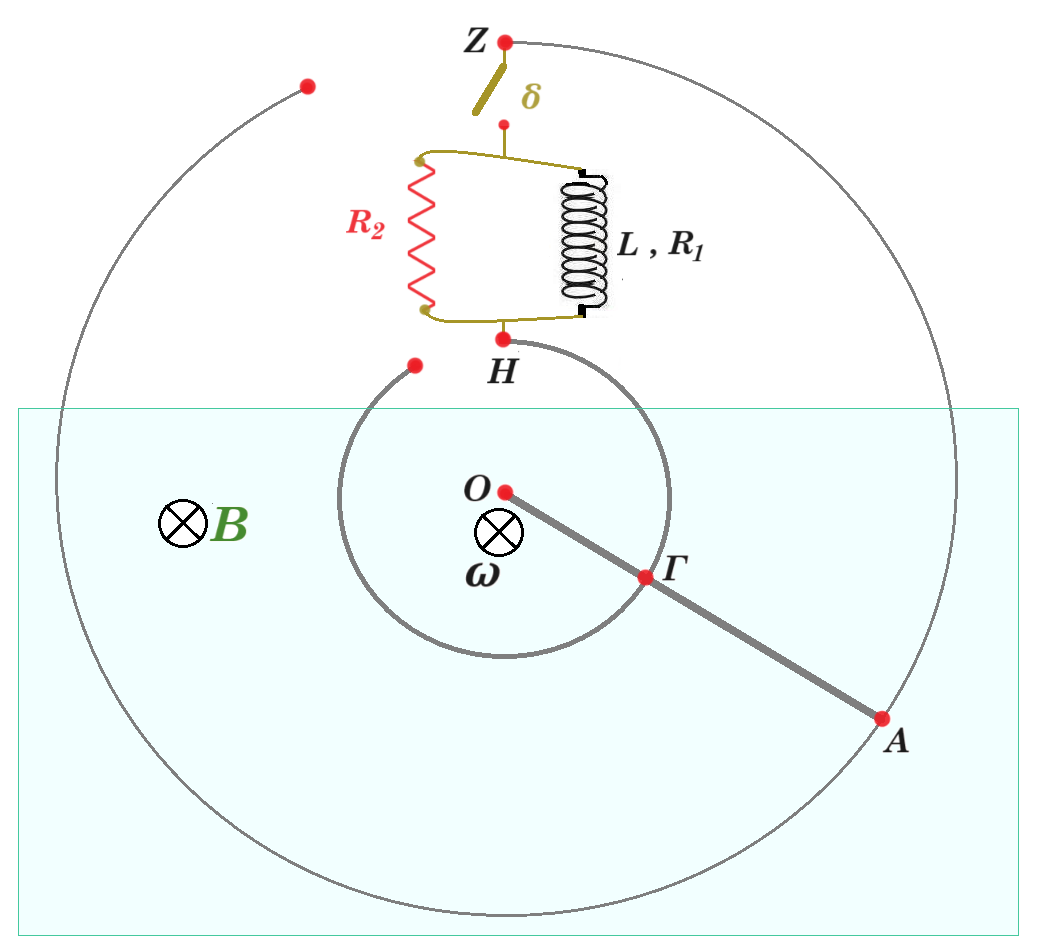
VΑΓ = Εεπαγ = Β [ π (ΟΑ)2 - π (ΟΓ)2 ] / Τ = Β [ π (ΟΑ)2 - π (ΟΓ)2 ] / (2π/ω) = [ (ΟΑ)2 - (ΟΓ)2 ] Β ω / 2 = ( 0,42 - 0,22 ) 1 2 / 2 = 0,16 - 0,04 = 0,12 V
VZH = VΑΓ = i2 R2 = L di1/dt + i1 R1 => 0,12 = i2 0,6 = 0,2 di1/dt + i1 1,2 => i2 = 0,12 / 0,6 = 0,2 A σταθερό
μόλις κλείσουμε τον διακόπτη i1 = 0 οπότε di1/dt = 0,12 / 0,2 = 0,6 A/s
μετά από πολύ χρόνο : i2 = 0,12 / 0,6 = 0,2 A 0,12 = - 0,2 di1/dt + i1 1,2 => 0,12 = i1 1,2 => i1 = 0,1 A UL = 0,5 L i12 = 0,5 0,2 0,12 = 0,001 J 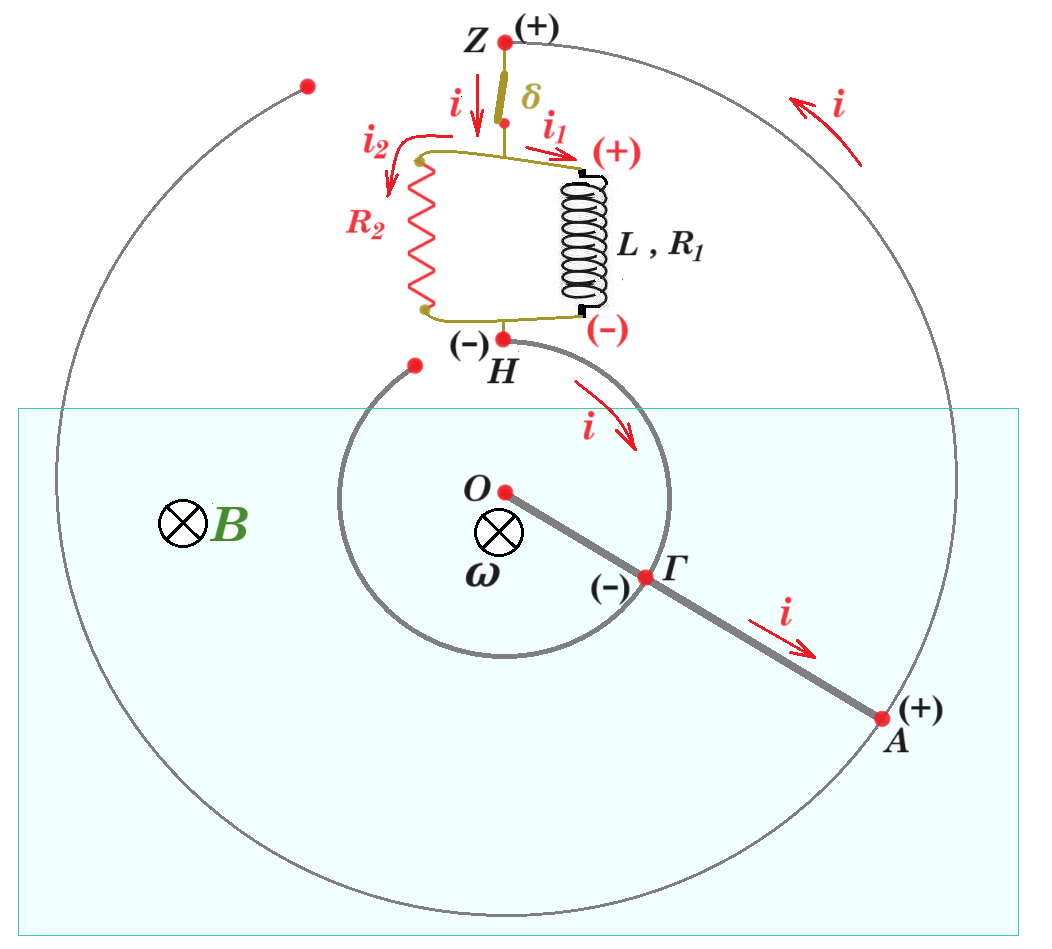
μόλις ανοίξουμε τον διακόπτη το πηνίο διαρρέεται από i = 0,1 A : - L di/dt = i (R1 + R2) => - 0,2 di/dt = 0,1 (1,2 + 0,6) => di/dt = - 1,8 / 2 = - 0,9 A/s 
ΘΕΜΑ Δ
Ομογενής κύλινδρος μάζας Μ και ακτίνας R = 5/π m βρίσκεται σε κεκλιμένο επίπεδο μεγάλου μήκους, γωνίας κλίσεως φ = 30°. Σε σημείο Α της επιφανείας του κυλίνδρου, το οποίο απέχει από την επιφάνεια του κεκλιμένου επιπέδου απόσταση 2R, έχει δεθεί το ένα άκρο αβαρούς και μη εκτατού νήματος. Το άλλο άκρο του νήματος έχει δεθεί σε σώμα Σ1 μικρών διαστάσεων και μάζας m1 = 1 kg.
Το νήμα περνά από το αυλάκι τροχαλίας ακτίνας r, η οποία έχει στερεωθεί σε οροφή. Το τμήμα (1) του νήματος είναι παράλληλο προς την επιφάνεια του κεκλιμένου επιπέδου, ενώ το τμήμα (2) κατακόρυφο.
Το σύστημα των σωμάτων αυτών ισορροπεί στο ίδιο κατακόρυφο επίπεδο. Ο άξονας του κυλίνδρου είναι κάθετος στο επίπεδο της σελίδας.
Σώμα Σ2 μικρών διαστάσεων και μάζας m2 = 4 kg ισορροπεί δεμένο στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 Ν/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο στο οριζόντιο δάπεδο. Ο άξονας του ελατηρίου βρίσκεται στην ίδια κατακόρυφη διεύθυνση με τη διεύθυνση του νήματος (2).
Δ1. Να υπολογίσετε τη μάζα Μ του κυλίνδρου. Μονάδες 5
Τη χρονική στιγμή t0 = 0, κόβουμε ταυτόχρονα τα νήματα (1) και (2).
Αμέσως μετά την t0 = 0, το σώμα Σ1 πέφτει κατακόρυφα ενώ ο κύλινδρος κατέρχεται στο κεκλιμένο επίπεδο με σταθερή επιτάχυνση, εκτελώντας κύλιση χωρίς ολίσθηση.
Κατά τη διάρκεια της κύλισής του ο άξονάς του παραμένει συνεχώς κάθετος στο επίπεδο της σελίδας.
Δ2. Αν τη χρονική στιγμή t1 το σημείο Α, ολοκληρώνει μία πλήρη περιστροφή και έχει ταχύτητα μέτρου υΑ = 20 m/s, να υπολογίσετε το μέτρο της επιτάχυνσης του κέντρου μάζας του κυλίνδρου κάνοντας χρήση των νόμων της κινηματικής κατά την κύλιση στερεών σωμάτων. Μονάδες 7
Το σώμα Σ1 πέφτοντας κατακόρυφα συγκρούεται κεντρικά και πλαστικά με το σώμα Σ2. Το συσσωμάτωμα, αμέσως μετά την πλαστική κρούση εκτελεί φθίνουσα ταλάντωση σε κατακόρυφη διεύθυνση, υπό την επίδραση δύναμης αντίστασης της μορφής Fαντ = -0,2υ (S.I.), όπου υ η αλγεβρική τιμή της ταχύτητας.
Αμέσως μετά την κρούση ο ρυθμός έκλυσης θερμικής ενέργειας στο περιβάλλον είναι ίσος με Pθ = 3,2 J/s. Να υπολογίσετε:
Δ3. το μέτρο της ταχύτητας του συσσωματώματος αμέσως μετά την πλαστική κρούση. Μονάδες 5
Δ4. τη συνολική θερμική ενέργεια που ελευθερώνεται στο περιβάλλον από τη χρονική στιγμή αμέσως μετά την κρούση έως την χρονική στιγμή που η ταλάντωση του συσσωματώματος σταματά. Μονάδες 8
Να θεωρήσετε ότι:
η επιτάχυνση της βαρύτητας g = 10 m/s2.
οι κρούσεις είναι ακαριαίες και κατά την πραγματοποίησή τους δεν έχουμε απώλεια μάζας.
το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλίας.
το σχήμα δεν είναι υπό κλίμακα.

Δ1. m1 g = T1 Στ(Ο) = 0 => T1 r = T2 r T2 = T1 = m1 g = 10 N
Στ(Κ) = 0 => T2 R = Tτρ R M g ημ30° = Τ2 + Ττρ = 2 Τ2 => Μ 10 ½ = 2 10 => Μ = 4 kg
Δ2. vA = vcm + ωR = 2 vcm = 2 ωR = 20 m/s => vcm = 10 m/s
ω = 10 m/s / 5/π m = 2π rad/s ο κύλινδρος κάνει μια στροφή άρα θ = 2π rad οπότε θ = ½ αγων t2 = ½ ω t => 2π = ½ 2π t => t = 2 s ω = αγων t => 2π = αγων 2 => αγων = π rad/s2
acm = αγων R = π 5/π = 5 m/s2
Δ3. Δ4. ισορροπία Σ1 : m1 g = k Δl1 => 40 = 100 Δl1 => Δl1 = 0,4 m
ισορροπία Σ1,2 : m1,2 g = k Δl12 => 50 = 100 Δl1,2 => Δl1,2 = 0,5 m x = 0,1 m βολής
μετά την κρούση ρυθμός έκλυσης θερμικής ενέργειας λόγω της Fαντ : Ρθερμ = Fαντ v = - b v v = - b v2 => - 3,2 = - 0,2 v2 => v2 = 16 => v = 4 m/s ταχύτητα συσσωματώματος αμέσως μετά την κρούση
αμέσως μετά την κρούση το συσσωμάτωμα έχει ενέργεια : ½ k x2 + ½ m1,2 v2 = ½ 100 0,12 + ½ 5 42 = 0,5 + 40 = 40,5 J
Qθερμ = 0 - 40,5 = - 40,5 J
επαναληπτικές ΣΕΠ 2022
ΘΕΜΑ Γ
Το σωληνοειδές μήκους l του σχήματος, που έχει n = 500 σπείρες/m και ωμική αντίσταση R1 = 2Ω, έχει συνδεθεί με θερμική συσκευή Σ ωμικής αντίστασης RΣ, η οποία, όταν στα άκρα της έχει τάση ίση με 10 V, λειτουργεί κανονικά αποδίδοντας θερμική ισχύ 50 W. Στα σημεία Κ, Λ του κυκλώματος έχει συνδεθεί κυκλικός αγωγός ωμικής αντίστασης R2=2Ω. Ο αγωγός αυτός αποτελείται από Ν = 300 σπείρες ίδιας ακτίνας, εμβαδού S = 0,25 m2 και βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο.
Το επίπεδο του αγωγού αυτού είναι κάθετο στις δυναμικές γραμμές του μαγνητικού πεδίου, οι οποίες έχουν φορά από τη
σελίδα προς τον αναγνώστη.
Το μέτρο της έντασης του μαγνητικού πεδίου αυξάνεται με σταθερό ρυθμό ΔΒ2/Δt = 0,16 T / s.
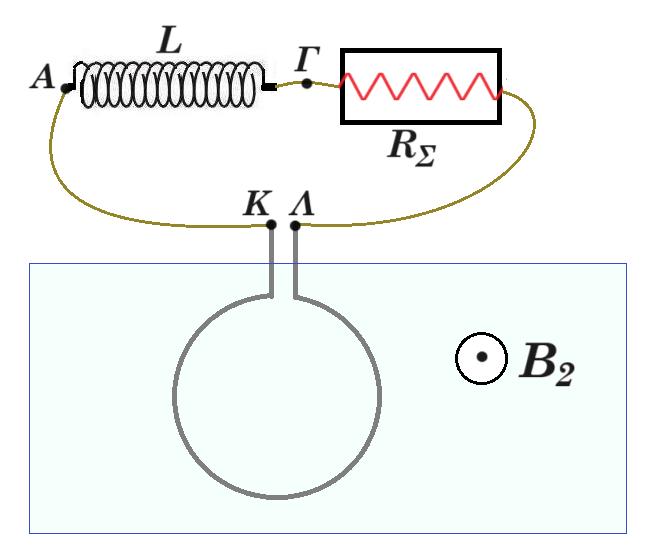
Γ1. Να σχεδιάσετε τη φορά του επαγωγικού ρεύματος στον κυκλικό αγωγό, αιτιολογώντας την απάντησή σας. Μονάδες 6
Γ2. Να υπολογίσετε την ηλεκτρεγερτική δύναμη (ΗΕΔ) από επαγωγή που αναπτύσσεται στον κυκλικό αγωγό. Μονάδες 6
Γ3. Να υπολογίσετε το μέτρο της έντασης B1 του μαγνητικού πεδίου στο κέντρο του σωληνοειδούς. Μονάδες 6
Γ4. Αποσυνδέουμε το σωληνοειδές από το κύκλωμα, το κόβουμε στη μέση και συνδέουμε ξανά το ένα από τα δύο νέα σωληνοειδή στα σημεία Α, Γ, διατηρώντας το μήκος l/2. Να υπολογίσετε το μέτρο της έντασης B1 του μαγνητικού πεδίου στο κέντρο του νέου σωληνοειδούς (μονάδες 4), καθώς και την τελική ισχύ που αποδίδει τότε η θερμική συσκευή. (μονάδες 3) Μονάδες 7
Δίνεται η σταθερά του μαγνητικού πεδίου Κμ =10-7 Ν/Α2. Να μη γίνει αντικατάσταση του π, όπου αυτό εμφανιστεί.
Εεπαγ = - ΔΦ/Δt = - N S ΔΒ2 / Δt = - 300 0,25 0,16 Volt = - 12 Volt
RΣ = V2 / P = 102 / 50 = 2 Ω Εεπαγ = i (R1 + R2 + RΣ) => 12 = i 6 => i = 2 A
B1 = 4π 10-7 i n = 4π 10-7 2 500 => Β1 = 4π 10-4 Τ
όταν κόψουμε το πηνίο στη μέση τότε κάθε κομμάτι θα έχει τη μισή ωμική αντίσταση R1/2 = 1 Ω χωρίς να αλλάξει ο συντελεστής n
η ένταση του ρεύματος στο κύκλωμα θα είναι Εεπαγ = i' (R1/2 + R2 + RΣ) => 12 = i' 5 => i' = 2,4 A
B1' = 4π 10-7 i' n = 4π 10-7 2,4 500 => Β1 = 4,8π 10-4 Τ
PΣ = i'2 RΣ = 2,42 2 = 11,52 Watt
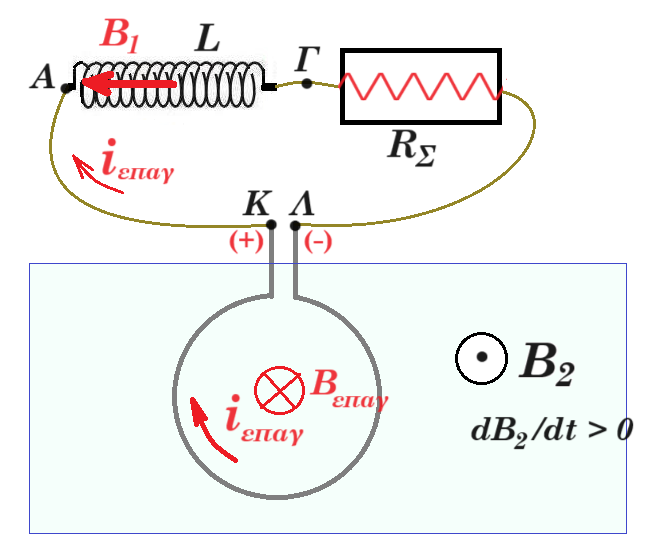
ΘΕΜΑ Δ
Άκαμπτη, ομογενής και ισοπαχής ράβδος ΑΒ, μήκους l = 1,2 m και μάζας Μρ = 2 Kg, έχει το άκρο της Α αρθρωμένο και ισορροπεί οριζόντια. Η ράβδος μπορεί να στρέφεται, χωρίς τριβές, σε κατακόρυφο επίπεδο γύρω από ακλόνητο
οριζόντιο άξονα που διέρχεται από το άκρο της Α.
Στο μέσον Γ της ράβδου ασκείται σταθερή κατακόρυφη δύναμη F με φορά προς τα πάνω, μέτρου F = 80 N. H ράβδος ΑΒ εφάπτεται με το άκρο της Β σε ομογενή τροχαλία, μάζας ΜΤ = 2 Kg και ακτίνας R, που είναι στερεωμένη σε οροφή και
που μπορεί να στρέφεται, χωρίς τριβές, γύρω από ακλόνητο οριζόντιο άξονα που διέρχεται από το κέντρο της και είναι κάθετος στο επίπεδό της.
Αβαρές και μη εκτατό νήμα είναι τυλιγμένο πολλές φορές στο αυλάκι της τροχαλίας και στο ελεύθερο άκρο του είναι δεμένο σώμα Σ1, μικρών διαστάσεων και μάζας m1 = 1 Kg. Η τροχαλία με την επίδραση της τριβής που δέχεται από τη
ράβδο ισορροπεί οριακά.
Δ1. Να υπολογίσετε το συντελεστή οριακής τριβής μεταξύ ράβδου και τροχαλίας καθώς και την δύναμη που δέχεται η ράβδος στην άρθρωση Α. Μονάδες 4
Τη χρονική στιγμή t0 = 0, καταργούμε τη δύναμη F, με αποτέλεσμα η ράβδος να στραφεί γύρω από το άκρο της Α και η τροχαλία να περιστρέφεται γύρω από τον άξονά της. Όταν η ράβδος φθάσει στην κατακόρυφη θέση, το άκρο της Β
συγκρούεται πλαστικά με ακίνητο σώμα Σ2, μικρών διαστάσεων και μάζας m2=1Kg.
Δ2. Να υπολογίσετε την ταχύτητα του σώματος Σ2 αμέσως μετά την κρούση. Μονάδες 6 (*) Αν το σώμα Σ2 φθάνει σε ύψος 0,24 m και η ράβδος σχηματίζει γωνία θ με την κατακόρυφη όταν ακινητοποιείται στιγμιαία, σε εκείνη τη θέση ποιος είναι ο ρυθμός μετααβολής της στροφορμής του συστήματος << ράβδου - Σ2 >>;
Κάτω από το σώμα Σ1 και σε απόσταση h = 1,2 m βρίσκεται σώμα Σ3, μάζας m3 = 3 Kg, το οποίο ισορροπεί στο άνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 N / m, η άλλη άκρη του οποίου είναι στερεωμένη σε σώμα Σ4 μάζας m4 = 2 Kg.
Τη χρονική στιγμή t1, το σώμα Σ1 συγκρούεται πλαστικά με το σώμα Σ3 και ταυτόχρονα κόβεται το νήμα. Αμέσως μετά την κρούση το συσσωμάτωμα εκτελεί απλή αρμονική ταλάντωση.
Δ3. Να υπολογίσετε το μέτρο της ταχύτητας υ1 του σώματος Σ1, τη χρονική στιγμή t1 που συναντά το σώμα Σ3. Μονάδες 4
Δ4. Να υπολογίσετε το πλάτος της απλής αρμονικής ταλάντωσης του συσσωματώματος. Μονάδες 5
Δ5. Αφού γράψετε τη χρονική εξίσωση της απομάκρυνσης του συσσωματώματος βρείτε την δύναμη που δέχεται το σώμα Σ4 από το οριζόντιο δάπεδο καθώς το συσσωμάτωμα ταλαντώνεται. Για ποιο πλάτος ταλάντωσης το Σ4 χάνει την επαφή του με το δάπεδο;
Θεωρήστε χρονική στιγμή t = 0 τη στιγμή της κρούσης και θετική φορά την προς τα κάτω. Μονάδες 6
Δίνονται:
• η επιτάχυνση της βαρύτητας g = 10 m/s2.
• η ροπή αδράνειας ράβδου ως προς άξονα που διέρχεται από το άκρο της Α : Ι(Α) = 1/3 Μρ l2
• η ροπή αδράνειας τροχαλίας ως προς τον άξονα της : Icm(T) = 1/2 MT R2
Να θεωρήσετε ότι:
• οι κρούσεις είναι ακαριαίες και κατά την πραγματοποίησή τους δεν έχουμε
απώλεια μάζας.
• η αντίσταση του αέρα θεωρείται αμελητέα για όλα τα σώματα.
• το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλίας.
• το σχήμα δεν είναι υπό κλίμακα.
Δ1.
στην ράβδο ασκούνται βάρος προς τα κάατω, η F προς τα πάνω, η αντίδραση Ν από την τροχαλία προς τα κάτω και από την άρθρωση FA
Στ(Α) = 0 => mg l/2 - F l/2 + N l = 0 => 20 1/2 - 80 1/2 + N = 0 => N = 30 N
ΣFy = 0 => F - N - mg + FA,y = 0 => 80 - 30 - 20 + FA,y = 0 => FA,y = - 30 N προς τα κάτω
τροχαλία : Στ(Ο) = 0 => m1 g R = Ts R => Ts = 10 N οριζόντια αριστερά
στην ράβδο ασκείται δύναμη τριβής Ts' = 10 N οριζόντια προς τα δεξιά μ = Ts' / N = 10 / 30 = 1/3
ΣFx = 0 => Ts' + FA,x = 0 => 10 + FA,x = 0 => FA,x = - 10 N οριζόντια αριστερά
FA2 = 102 + 302 = 1000 => FA = 10√10 N
Δ2.
διατήρηση ενέργειας : Mρ g l/2 = 0,5 1/3 Mρ l2 ω2 => g = 1/3 l ω2 => 10 = 1/3 1,2 ω2 => ω2 = 30/1,2 = 300/12 = 100/4 = 25 => ω = 5 rad/s πριν την κρούση
πλαστική κρούση διατήρηση στροφορμής : 1/3 Mρ l2 ω = ( 1/3 Mρ l2 + m2 l2 ) ω' => 1/3 2 1,22 5 = ( 1/3 2 1,22 + 1 1,22 ) ω' => 1/3 2 5 = 5/3 ω' => ω' = 2 rad/s
v2 = ω' l = 2 1,2 = 2,4 m/s
(*) έστω ότι το σώμα Σ2 ανέρχεται σε ύψος h μετά την κρούση και η ράβδος σχηματίζει γωνία θ με την κατακόρυφη τότε h = l - l συνθ = l (1 - συνθ)
διατήρηση ενέργειας : ½ ( 1/3 Mρ l2 + m2 l2 ) (ω')2 = m2 g l (1 - συνθ) + Mρ g l/2 (1 - συνθ)
½ ( 1/3 2 1,22 + 1 1,22 ) 22 = 1 10 1,2 (1 - συνθ) + 2 10 0,6 (1 - συνθ) =>
½ 5/3 1,2 4 = 10 (1 - συνθ) + 10 (1 - συνθ) => 4 = 20 (1 - συνθ) => 1 - συνθ = 4/20 = 0,2 => συνθ = 0,8 ημθ = 0,6 άρα h = l (1 - συνθ) = 1,2 (1 - 0,8) => h = 0,24 m
στη θέση αυτή dL/dt = Στ(Α) = Μρ g l/2 ημθ + m2 g l ημθ = 20 0,6 0,6 + 10 1,2 0,6 = 24 0,6 = 14,4 Νm = 14,4 kg m2/s2
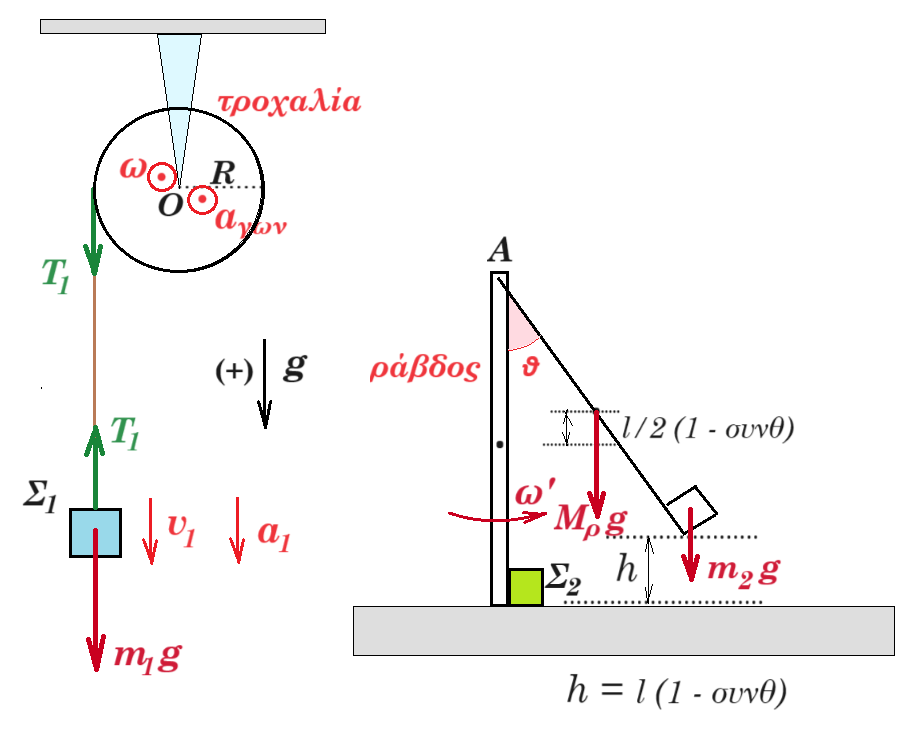
Δ3.
περιστροφή τροχαλίας : Στ(Ο) = Ιτροχ αγων => T1 R = 1/2 MΤ R2 αγων => T1 = 1/2 2 R αγων => T1 = R αγων = α1
κατακόρυφη κίνηση Σ1 : m1 g - T1 = m1 a1 => 10 - α1 = 1 a1 => 2 α1 = 10 => α1 = 5 m/s2
h = 0,5 a1 t2 => 1,2 = 0,5 5 t2 => t = √0,48 s
v1 = a1 t = 5 √0,48 = √12 m/s = 2√3 m/s
Δ4.
ισορροπία Σ3 : m3 g = k Δl => 3 10 = 100 Δl => Δl = 0,3 m συσπείρωση
ισορροπία Σ1,3 : m1,3 g = k Δl => 4 10 = 100 Δl => Δl' = 0,4 m συσπείρωση
διατήρηση ορμής πλαστική κρούση : m1 v1 = m1,3 u => 1 √12 = 4 u => u = √3/2 m/s
0,5 k Δl2 + 0,5 m1,3 u2 = 0,5 k A2 => 100 0,12 + 4 3/4 = 100 A2 => 1 + 3 = 100 A2 => A2 = 0,04 => A = 0,2 m
Δ5.
k = m1,3 ω2 => 100 = 4 ω2 => ω = 5 rad/s
x = 0,2 ημ(5t + θ) - 0,1 = 0,2 ημθ => ημθ = - 0,5 => θ = π + π/6 = 7π/6
οπότε συν(7π/6) = - √3/2 < 0 απορρίπτεται διότι υ > 0 προς τα κάτω κίνηση
άρα θ = 2π - π/6 = 11π/6 οπότε συνθ = + √3/2 > 0 υ > 0
x = 0,2 ημ(5t + 11π/6) υ = 1 συν(5t + 11π/6) α = - 5 ημ(5t + 11π/6)
ΣF = m1,3 a => m1,3 g + Fελατ = m1,3 a => 40 + Fελατ = 4 ( - 5 ημ(5t + 11π/6) ) =>
=> Fελατ(t) = - 40 - 20 ημ(5t + 11π/6) ή Fελατ(x) = - 100 (0,4 + x) όπου - 0,2m £ x £ +0,2m τη στιγμή t = 0 x = - 0,1 m ημθ = - 0,5 το ελατήριο είναι συσπειρωμένο κατά Δl = 0,3 m άρα η δύναμη ελατηρίου είναι Fελατ = - 100N/m 0,3 m = - 30 N κατακόρυφη προς τα πάνω ( θετική προς τα κάτω )
στο κάτω άκρο του ελατηρίου η δύναμη έχει εξίσωση F'ελατ = 40 + 20 ημ(5t + 11π/6)
οπότε το σώμα Σ4 δέχεται δυνάμεις : ΣF = 0 => m4 g - N4 + F'ελατ = 0 =>
=> 20 - N4 + 40 + 20 ημ(5t + 11π/6) = 0 => Ν4 = 60 + 20 ημ(5t + 11π/6)
τη στιγμή t = 0 x = - 0,1 m ημθ = - 0,5 το ελατήριο είναι συσπειρωμένο κατά Δl = 0,3 m άρα η δύναμη ελατηρίου είναι Fελατ = - 100N/m 0,3 m = - 30 N κατακόρυφη προς τα πάνω ( θετική προς τα κάτω ) το Σ4 δέχεται από το ελατήριο δύναμη 30 Ν προς τα κάτω επίσης δέχεται το βάρος του 20 Ν προς τα κάτω συνεπώς η αντίδραση Ν4 από το δάπεδο είναι 50 Ν προς τα πάνω πράγματι
Ν4 = 60 + 20 ημ(5t + 11π/6) = 60 + 20 (- 0,5) = + 50 Ν
το Σ4 για να χάσει την επαφή του με το δάπεδο πρέπει να μηδενισθεί η Ν4 αυτό συμβαίνει όταν το πλάτος ταλάντωσης του συσσωματώματος Σ1,3 γίνεται ίσο με Α = 0,4m + 0,2m = 0,6m πρέπει να βρεθεί το Σ1,3 πάνω από τη Θ.Ι. του ( 0,4m ) και να έχει το ελατήριο επιμήκυνση ( 0,2m ) ώστε η δύναμη ελατηρίου για το Σ1,3 να ισούται με 20 Ν = 100 Ν/m 0,2 m με φορά προς τα κάτω ενώ για το Σ4 η δύναμη ελατηρίου ισούται με 20 Ν με φορά προς τα πάνω και έτσι εξουδετερώνεται το βάρος του Σ4
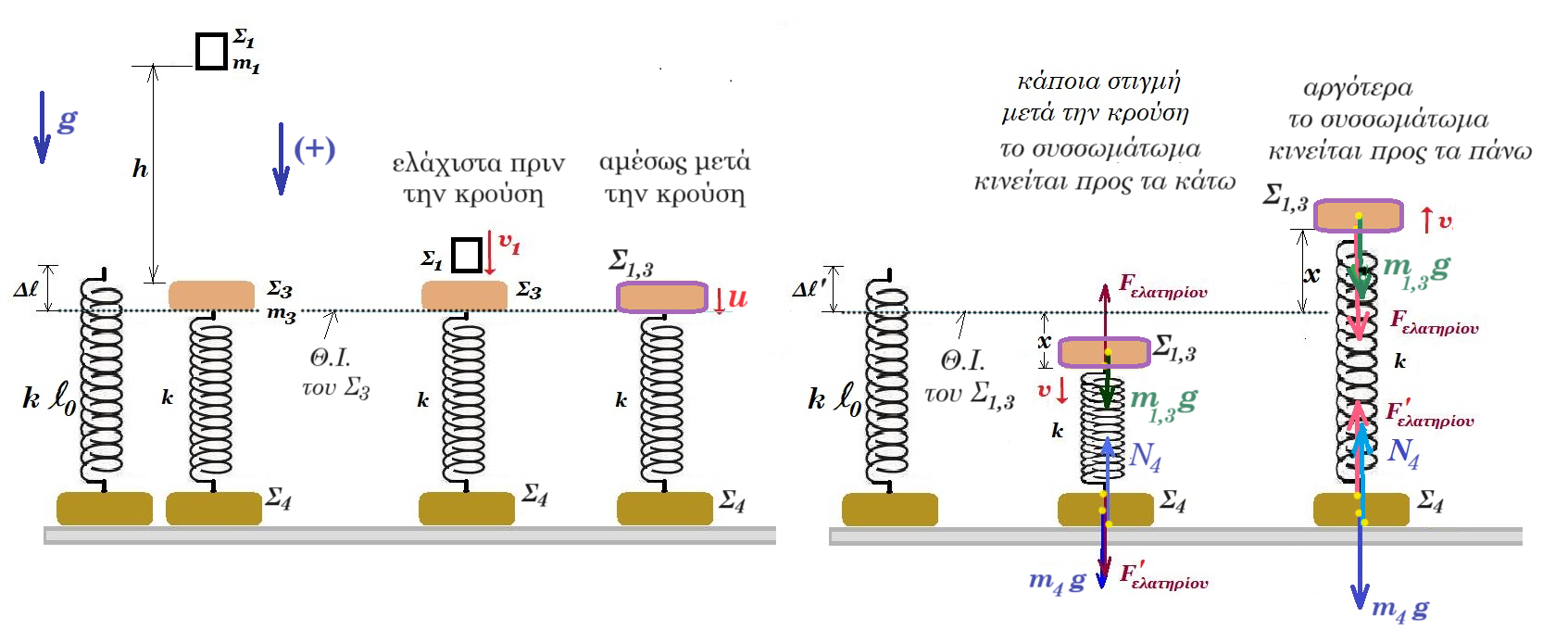
επαναληπτικές ΣΕΠ 2021
ΘΕΜΑ Γ
Οι δύο παράλληλοι οριζόντιοι αγωγοί, Αx και Γy έχουν μεγάλο μήκος, αμελητέα ωμική αντίσταση και απέχουν μεταξύ τους απόσταση l = 1 m. Τα άκρα τους Α και Γ συνδέονται με σωληνοειδές ωμικής αντίστασης R1 = 6 Ω, του οποίου ο αριθμός των σπειρών ανά μονάδα μήκους είναι n = N/l = 200 σπείρες/m.
Στα σημεία Δ και Ζ των παράλληλων αγωγών έχει συνδεθεί ηλεκτρική πηγή με ηλεκτρεγερτική δύναμη Ε = 24 V και εσωτερική αντίσταση r = 2 Ω. Στα σημεία Η και Θ συνδέεται αντιστάτης ωμικής αντίστασης R3 = 1 Ω σε σειρά με τον
διακόπτη δ2, ενώ μεταξύ των σημείων Ζ και Θ παρεμβάλλεται διακόπτης δ1.
Ευθύγραμμος μεταλλικός αγωγός ΚΛ, μάζας m = 1 Kg, μήκους L = 1 m και ωμικής αντίστασης R2 = 3 Ω, του οποίου τα άκρα βρίσκονται συνεχώς σε επαφή με τους αγωγούς Αx και Γy και μπορεί να ολισθαίνει παραμένοντας συνεχώς
κάθετος σε αυτούς. Στην γραμμοσκιασμένη περιοχή του επιπέδου των αγωγών Αx και Γy εφαρμόζεται εξωτερικό ομογενές μαγνητικό πεδίο έντασης Β = 1 Τ, του οποίου οι μαγνητικές γραμμές είναι κάθετες στο επίπεδο αυτό,
με φορά από την σελίδα προς τον αναγνώστη.
Αρχικά ο διακόπτης δ1 είναι κλειστός και ο διακόπτης δ2 ανοιχτός. Ο αγωγός ΚΛ ισορροπεί οριακά λόγω τριβής, που εμφανίζεται στα σημεία επαφής Κ και Λ, συνολικού μέτρου Τ.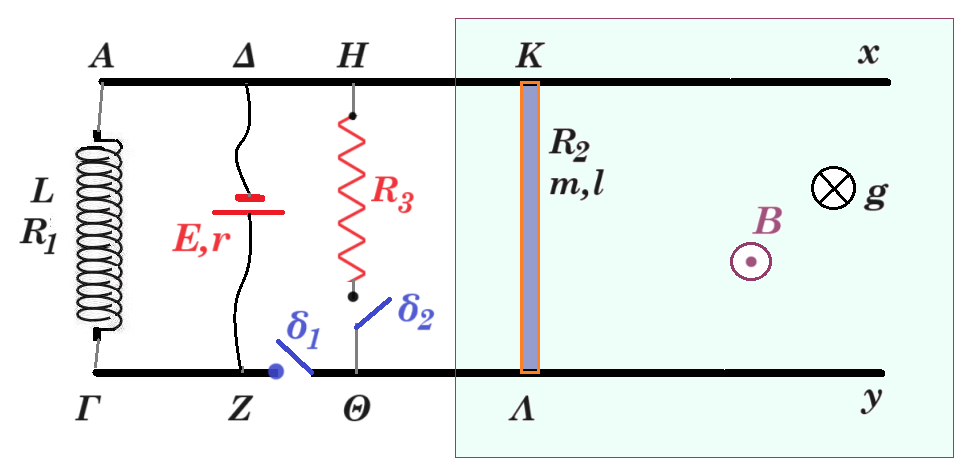
Γ1. Να υπολογίσετε το μέτρο της δύναμης τριβής Τ. Μονάδες 6
Γ2. Να υπολογίσετε την ένταση του μαγνητικού πεδίου στο μέσον του άξονα του σωληνοειδούς. Θεωρείστε πως τα δύο μαγνητικά πεδία δεν αλληλεπιδρούν. Μονάδες 6
Τη χρονική στιγμή t0 = 0 κλείνουμε τον διακόπτη δ2 και ανοίγουμε τον διακόπτη δ1. Την ίδια στιγμή στο μέσον του αγωγού ΚΛ και κάθετα σε αυτόν ασκείται κατάλληλη δύναμη F με φορά προς τα δεξιά, ώστε αυτός να κινείται με σταθερή επιτάχυνση α = 4 m/s2 ίδιας κατεύθυνσης με την δύναμη F.
Γ3. Να γράψετε τη σχέση που δίνει την εξωτερική δύναμη σε συνάρτηση με τον χρόνο F = F(t).
Η συνολική τριβή του αγωγού ΚΛ με τους οριζόντιους αγωγούς σε όλη τη διάρκεια της κίνησής του είναι ίση με Τ. Μονάδες 7
Γ4. Να υπολογίσετε το επαγωγικό φορτίο που πέρασε από μία διατομή του αγωγού, ΚΛ στο χρονικό διάστημα από t0 = 0 έως t1 = 1 s. Μονάδες 6
Η διάταξη κατά τη διάρκεια της κίνησης του αγωγού ΚΛ παραμένει ακίνητη.
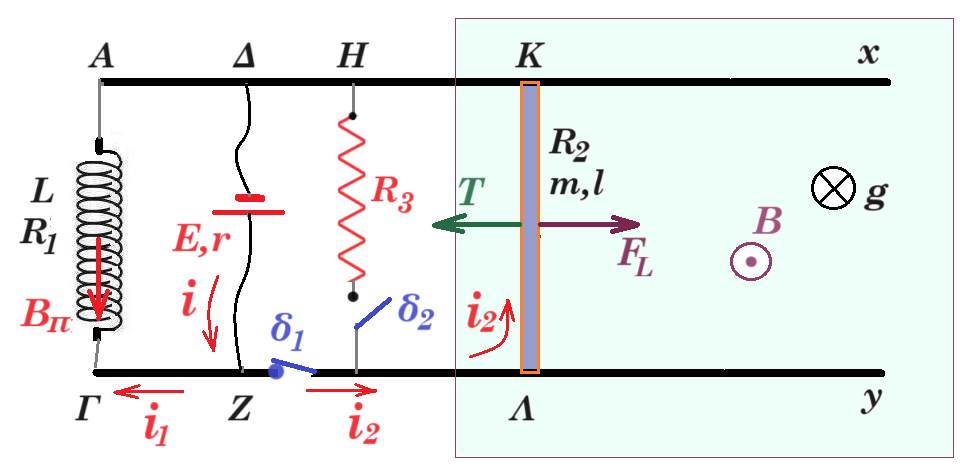 Γ1. R1,2 = R1 R2 / (R1 + R2) = 6 3 / 9 = 2 Ω Ε = i (r + R1,2) => 24 V = i (2 Ω + 2 Ω) => i = 6 A
Γ1. R1,2 = R1 R2 / (R1 + R2) = 6 3 / 9 = 2 Ω Ε = i (r + R1,2) => 24 V = i (2 Ω + 2 Ω) => i = 6 A
VZΔ = Vπολική = Ε - i r = 24 - 6 2 = 12 Volt i1 = VZΔ / R1 = 12 V / 6 Ω = 2 A
i2 = VZΔ / R2 = 12 V / 3 Ω = 4 A Fl = B l i2 = 1 T 1 m 4 A = 4 N FL + T = 0 => T = - 4 N
Γ2. Βπ = 4π 10-7 i1 n = 4π 10-7 2 200 => Βπ = 16π 10-5 T
Γ3. v = a t => v = 4 t
Eεπαγ = i (R2 + R3) => B l v = i (R2 + R3) => 1 1 v = i (3 + 1) => v = 4i => i = v/4 = t
FL = B l i = 1 1 v/4 => FL = v/4 = t
F - T - FL = m a => F - 4 - t = 1 4 => F(t) = 8 + t
Γ4. i = dq / dt => dq = i dt = t dt => dq = t dt => q(t) = 0,5 t2 q(0) = 0 q(1) = 0,5 C
ή αλλιώ; από το εμβαδόν του τριγώνου στο διάγραμμα i(t) = t από t = 0 έως t = 1 s
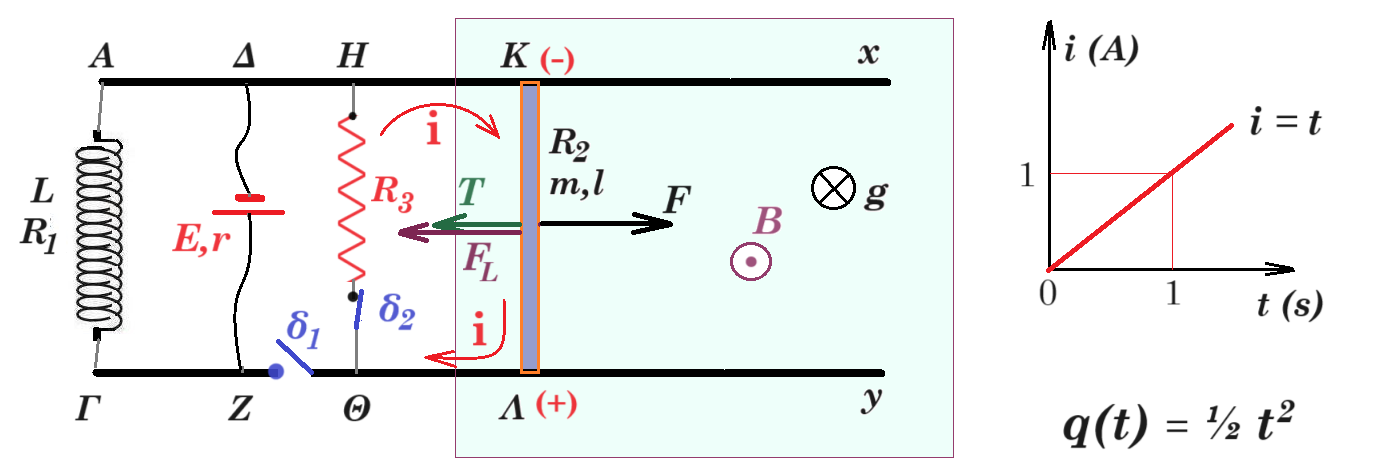
επαναληπτικές ΣΕΠ 2020
ΘΕΜΑ Γ
Οι κατακόρυφοι, μεγάλου μήκους, μεταλλικοί αγωγοί Αx και Γy απέχουν μεταξύ τους σταθερή απόσταση l = 1m και έχουν αμελητέα ωμική αντίσταση. Τα άκρα Α και Γ συνδέονται με αντιστάτη ωμικής αντίστασης R1 = 2Ω. Στο τμήμα ΑΓ υπάρχει διακόπτης δ, ο οποίος είναι κλειστός.
Ο αγωγός ΚΛ μήκους l = 1m, μάζας m = 0,2kg και ωμικής αντίστασης R2 = 6Ω έχει τα άκρα του ΚΛ πάνω στους κατακόρυφους αγωγούς Αx και Γy και είναι κάθετος σε αυτούς.
Όλη η διάταξη βρίσκεται σε περιοχή που επικρατεί οριζόντιο ομογενές μαγνητικό πεδίο έντασης B, μέτρου Β = 2T, του οποίου οι δυναμικές γραμμές είναι κάθετες στο επίπεδο του σχήματος με φορά από τον αναγνώστη προς τη σελίδα. Ο αγωγός ΚΛ μπορεί να ολισθαίνει κατά μήκος των αγωγών Αx και Γy χωρίς τριβές, παραμένοντας συνεχώς οριζόντιος, χωρίς τα άκρα του Κ και Λ να χάνουν την επαφή με τους αγωγούς Αx και Γy. Αρχικά ο αγωγός είναι ακίνητος.
Ο αγωγός ΚΛ μπορεί να ολισθαίνει κατά μήκος των αγωγών Αx και Γy χωρίς τριβές, παραμένοντας συνεχώς οριζόντιος, χωρίς τα άκρα του Κ και Λ να χάνουν την επαφή με τους αγωγούς Αx και Γy. Αρχικά ο αγωγός είναι ακίνητος.
Τη χρονική στιγμή t0=0 εκτοξεύουμε τον αγωγό ΚΛ κατακόρυφα προς τα κάτω με αρχική ταχύτητα μέτρου υ0 = 12m/s.
Γ1. Να βρείτε το μέτρο της επιτάχυνσης α του αγωγού αμέσως μετά την εκτόξευσή του (μονάδες 3) και την κατεύθυνσή της (μονάδες 2). Μονάδες 5
Γ2. Τη χρονική στιγμή t1, που ο αγωγός ΚΛ έχει μετατοπιστεί κατά h από την αρχική του θέση, έχει αποκτήσει οριακή ταχύτητα ( υορ ). Να υπολογίσετε το μέτρο της οριακής ταχύτητας. Μονάδες 5
Γ3. Αν το φορτίο που πέρασε από μία διατομή του αγωγού ΚΛ από τη χρονική στιγμή t0 = 0 έως τη χρονική στιγμή t1 είναι ίσο με 0,4C, να υπολογίσετε τη θερμότητα που παράχθηκε σε καθέναν από τους αντιστάτες R1 και R2 στο
παραπάνω χρονικό διάστημα. Μονάδες 8
Γ4. Κάποια χρονική στιγμή t2 (t2 > t1), που ο αγωγός ΚΛ κινείται με την οριακή του ταχύτητα, ανοίγουμε το διακόπτη δ. Τη χρονική στιγμή t3 = t2 + Δt ο αγωγός έχει μετατοπιστεί κατά h1 = 0,45 m από τη θέση στην οποία βρισκόταν τη χρονική στιγμή t2. Να υπολογίσετε το ρυθμό (dK/dt ) με τον οποίο αυξάνεται η κινητική ενέργεια του αγωγού τη χρονική στιγμή t3. Μονάδες 7
• Δίνεται η επιτάχυνση της βαρύτητας: g = 10 m/s2
• Η αντίσταση του αέρα θεωρείται αμελητέα.

Γ1. ο αγωγός ΚΛ κινούμενος με ταχύτητα υ0 μέσα στο μαγνητικό πεδίο, στα άκρα του εμφανίζεται επαγωγική τάση Eεπαγ = B l v0 διότι τα ηλεκτρόνιά του δέχονται δύναμη Lorentz και κινούνται προς το άκρο Κ το οποίο αποκτά αρνητικό φορτίο, ενώ το άρο Λ αποκτά θετικό φορτίο, έτσι κλείνει κύκλωμα και ισχύει ο νόμος του Ohm : Eεπαγ = B l v0 = i (R1 + R2) => 2Τ 1m 12m/s = i (2Ω + 6Ω) => i = 3A
ο αγωγός ΚΛ διαρρέεται από ρεύμα κινούμενος μέσα στο μαγνητικό πεδίο δέχεται δύναμη Laplace FL = Bli = 2T 1m 3A = 6 N
ΣF = m a => mg - FL = m a => 2N - 6N = 0,2kg a => a = - 20 m/s2 επιβράδυνση αγωγού ΚΛ
Γ2. ο αγωγός ΚΛ επιβραδύνεται η ταχύτητα του μειώνεται η επαγωγική τάση μειώνεται το ρεύμα μειώνεται η δύναμη Laplace μειώνεται το μέτρο της επιτάχυνσης μειώνεται και κάποια στιγμή μηδενίζεται τότε mg - FL = 0 => mg - B l i = 0 => 2 - 2 1 i = 0 => i = 1 A οπότε ο αγωγός αποκτά οριακή ταχύτητα υορ : B l vορ = i (R1 + R2) => 2Τ 1m υορ = 1Α (2Ω + 6Ω) => υορ = 4m/s
Γ3. q = ΔΦ / (R1 + R2) => q = B l h / (R1 + R2) => 0,4 = 2 1 h / 8 => h = 1,6 m
διατήρηση ενέργειας : ½ m v02 + m g h = ½ m vορ2 + Qθερμ => ½ 0,2 122 + 0,2 10 1,6 = ½ 0,2 42 => 14,4 + 3,2 = 1,6 + Qθερμ => Qθερμ = 16 J
Qθερμ / (R1 + R2) = Q1 / R1 = Q2 / R2 => 16 / 8 = Q1 / 2 = Q2 / 6 => Q1 = 4 J Q2 = 12 J
B l v = i (R1 + R2) => i = B l v / (R1 + R2)
mg - FL = m a => mg - B l i = m a => mg - B l B l v / (R1 + R2) = m a =>
=> mg - B2 l2 v / (R1 + R2) = m dv/dt => 2 - 4 v / 8 = 0,2 dv/dt => 4 - v = 0,4 dv/dt =>
=> v - 4 = - 0,4 dv/dt => dv / (v - 4) = - 2,5 dt => ln [ (v - 4) / (12 - 4) ] = - 2,5 t =>
=> v(t) = 4 + 8 e- 2,5 t
v(0) = 4 + 8 = 12 m/s v(2) = 4 m/s t = 5τ = 5 1/2,5 s = 5 0,4 s = 2 s
a(t) = dv/dt = - 2,5 8 e- 2,5 t = - 20 e- 2,5 t a(0) = - 20 m/s2 a(2) = - 20 0 = 0
v = dx/dt => dx = v dt = ( 4 + 8 e- 2,5 t ) dt => x(t) = 4t + (- 0,4) 8 ( e- 2,5 t - e0 )
x(t) = 4t - 3,2 ( e- 2,5 t - 1 ) t = 0 : x(0) = 0 t = 2s : x(2) = 8 + 3,2 = 11,2 m
i = B l v / (R1 + R2) = 2 1 ( 4 + 8 e- 2,5 t ) / 8 = ( 4 + 8 e- 2,5 t ) / 4 => i(t) = 1 + 2 e- 2,5 t
i = dq/dt => dq = i dt = ( 1 + 2 e- 2,5 t ) dt => q(t) = t - 2 0,4 ( e- 2,5 t - e0 ) =>
q(t) = t - 0,8 ( e- 2,5 t - 1 ) q(0) = 0 q(2) = 2 - 0,8 (0 - 1) = 2,8 Cb
v(t) = 4 + 8 e- 2,5 t
v(0) = 4 + 8 = 12 m/s v(2,4) = 4 m/s t = 6τ = 6 1/2,5 s = 6 0,4 s = 2,4 s
a(t) = dv/dt = - 2,5 8 e- 2,5 t = - 20 e- 2,5 t a(0) = - 20 m/s2 a(2,4) = - 20 0 = 0
v = dx/dt => dx = v dt = ( 4 + 8 e- 2,5 t ) dt => x(t) = 4t + (- 0,4) 8 ( e- 2,5 t - e0 )
x(t) = 4t - 3,2 ( e- 2,5 t - 1 ) t = 0 : x(0) = 0 t = 2,4s : x(2,4) = 9,6 + 3,2 = 12,8 m
Γ4. ανοίγουμε τον διακόπτη h1 = vορ Δt + 0,5 g Δt2 => 0,45 = 4 Δt + 0,5 10 Δt2
=> 5 Δt2 + 4 Δt - 0,45 = 0 => Δt2 + 0,8 Δt - 0,09 = 0 Δ = 0,64 + 0,36 = 1
Δt = ( - 0,8 + 1 ) / 2 = 0,1 s v' = vορ + g Δt = 4 + 10 0,1 => v' = 5 m/s
dK/dt = m v' a = m v' g = 0,2 5 10 => dK/dt = + 10 J/s
ΘΕΜΑ Δ NEO
Σώμα Σ1 με μάζα m1 = 5kg ηρεμεί πάνω σε λείο οριζόντιο επίπεδο, συνδεδεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k1 = 80Ν/m, του οποίου το άλλο άκρο είναι δεμένο σε ακλόνητο σημείο Α. Όμοια, σώμα Σ2 με μάζα m2 = 12kg, ηρεμεί πάνω στο ίδιο οριζόντιο επίπεδο, συνδεδεμένο στο άκρο ενός άλλου ιδανικού ελατηρίου σταθεράς k2 = 300Ν/m, του οποίου το άλλο άκρο είναι δεμένο σε ακλόνητο σημείο Γ. Τα σώματα στις θέσεις ισορροπίας τους (Θ.Ι.1) και (Θ.Ι.2) απέχουν μεταξύ τους απόσταση d = 0,6m.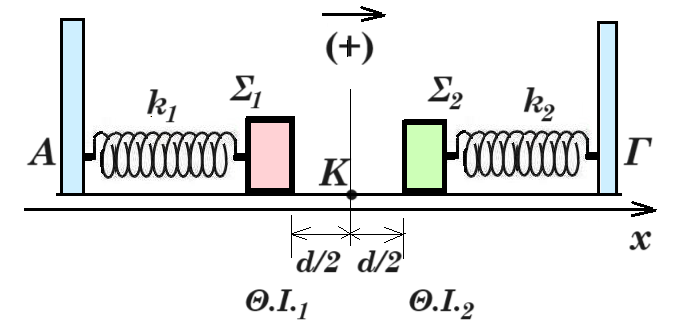
Δ1. Αν τα σώματα Σ1 και Σ2 εκτελούσαν απλή αρμονική ταλάντωση με σταθερά ταλάντωσης D1 = k1 και D2 = k2, να υπολογίσετε την περίοδο τους. Μονάδες 4
Απομακρύνουμε το σώμα Σ1 από τη θέση ισορροπίας του προς τα αριστερά κατά μήκος d1 = 0,6m και το σώμα Σ2 από τη θέση ισορροπίας του προς τα δεξιά κατά μήκος d2 = 0,23m. Τη χρονική στιγμή t0 = 0 αφήνουμε τα σώματα Σ1 και Σ2 ελεύθερα να κινηθούν.
Δ2. Θεωρώντας θετική φορά από το Α προς το Γ, να γράψετε τις εξισώσεις για τις απομακρύνσεις των δύο σωμάτων από τις θέσεις ισορροπίας τους και τις ταχύτητές τους, σε συνάρτηση με τον χρόνο t. Μονάδες 5
Δ3. Αποδείξτε ότι τα δύο σώματα θα συγκρουστούν στο μέσον Κ των αρχικών θέσεων ισορροπίας. Μονάδες 6
Δ4. Τα σώματα συγκρούονται κεντρικά και ελαστικά. Υπολογίστε τις ταχύτητες των δύο σωμάτων αμέσως πριν και αμέσως μετά την κρούση. Μονάδες 7
Δ5. Να δείξετε ότι στη συνέχεια τα δύο σώματα συγκρούονται ξανά στο σημείο Κ. Μονάδες 3
Δ1. k1 = m1 ω12 => 80 = 5 ω12 => ω1 = 4 rad/s T1 = 2π/ω1 = 2π/4 = π/2 s
k2 = m2 ω22 => 300 = 12 ω22 => ω2 = 5 rad/s T2 = 2π/ω2 = 2π/5 s
Δ2. x1 = 0,6 ημ(4t + 3π/2) v1 = 2,4 συν(4t + 3π/2) a1 = - 9,6 ημ(4t + 3π/2)
x2 = 0,2√3 ημ(5t + π/2) v2 = √3 συν(5t + π/2) a2 = - 5√3 ημ(5t + π/2)
Δ3. x1 = + 0,3 m => 0,6 ημ(4t + 3π/2) = + 0,3 => ημ(4t + 3π/2) = + ½
το Σ1 για να πάει από τη θέση -Α στη θέση +Α/2 θέλει χρόνο : T1 / 4 + T1 / 12 = T1 / 3 = π/6 s
x2 = - 0,3 m => 0,2√3 ημ(5t + π/2) = - 0,3 => ημ(5t + π/2) = - √3/2
το Σ2 για να πάει από τη θέση +Α στη θέση -√3A/2 θέλει χρόνο : T2 / 4 + T2 / 6 = 5T2 / 12 = 5/12 2π/5 s = π/6 s
τα δύο σώματα τα αφήνουμε ταυτόχρονα από τις ακρέες θέσεις και φθάνουν στον ίδιο χρόνο π/6 s στο σημείο Κ
Δ4. x1 = + 0,3 m => 0,6 ημ(4t + 3π/2) = + 0,3 => ημ(4t + 3π/2) = + ½
συν(4t + 3π/2) = + √3/2 > 0 διότι το Σ1 κινείται προς τα δεξιά
v1 = 2,4 συν(4t + 3π/2) = 2,4 (+ √3/2 ) => v1 = + 1,2√3 m/s
x2 = - 0,3 m => 0,2√3 ημ(5t + π/2) = - 0,3 => ημ(5t + π/2) = - √3/2
συν(5t + π/2) = - 1/2 διότι το Σ2 κινείται προς τα αριστερά
v2 = √3 συν(5t + π/2) => v2 = - √3/2 m/s
κεντρική ελαστική κρούση :
v1' = v1 (m1 - m2) / (m1 + m2) + 2 m2 v2 / (m1 + m2) =
= 1,2√3 (5 - 12) / (5 + 12) + 2 12 (- √3/2 ) / (5 + 12) =
= - 1,2√3 7 / 17 - 12√3 / 17 = - 20,4√3 / 17 m/s => v1' = - 1,2√3 m/s = - v1
v2' = v2 (m2 - m1) / (m1 + m2) + 2 m1 v1 / (m1 + m2) =
= - √3/2 (12 - 5) / 17 + 2 5 1,2√3 / 17 = - √3/2 7 / 17 + 12√3 / 17 =
= ( 24√3 - √3 7 ) / (2 . 17) => v2' = + √3/2 m/s = - v2
Δ5. το Σ1 για να πάει από τη θέση +Α/2 στη θέση +Α/2 θέλει χρόνο : 2 { T1 / 4 + T1 / 12 } = 2 T1 / 3 = π/3 s
το Σ2 για να πάει από τη θέση -√3A/2 στη θέση -√3A/2 θέλει χρόνο : 2 { T2 / 4 + T2 / 6 } = 2 5T2 / 12 = 5/6 2π/5 s = π/3 s
τα δύο σώματα θα συγκρουστούν πάλι μετά από χρόνο π/3 s στο σημείο Κ
ΠΑΛΑΙΟ 2020
A1. Η εξίσωση της απομάκρυνσης της ταλάντωσης σώματος μάζας m με ιδανικό ελατήριο σταθεράς Κ, δίνεται από τη σχέση: x = A ημ( √(2k/m) t + φ0 ),
όπου Α το σταθερό πλάτος. Η παραπάνω ταλάντωση είναι
α) φθίνουσα.
β) ελεύθερη.
γ) εξαναγκασμένη σε συντονισμό.
δ) εξαναγκασμένη αλλά όχι σε συντονισμό. Μονάδες 5
A3. Ένα στερεό σώμα αρχικά ακίνητο, δέχεται μόνο 2 δυνάμεις την F1 και την F2, που είναι αντίθετες και δεν έχουν τον ίδιο φορέα. Το παραπάνω σώμα
α) θα παραμείνει ακίνητο.
β) θα εκτελέσει μόνο στροφική κίνηση.
γ) θα εκτελέσει μόνο μεταφορική κίνηση.
δ) θα εκτελέσει σύνθετη κίνηση που αποτελείται από μία μεταφορική και μία στροφική. Μονάδες 5
ΘΕΜΑ Γ
Εγκάρσιο αρμονικό κύμα διαδίδεται σε ομογενές γραμμικό ελαστικό μέσο (χορδή) κατά μήκος της ημιευθείας Οx προς τη θετική κατεύθυνση. Η διάδοση του κύματος γίνεται χωρίς απώλειες ενέργειας. Η πηγή του κύματος βρίσκεται
στο άκρο Ο της χορδής. Δύο υλικά σημεία της χορδής ίδιας στοιχειώδους μάζας Δm βρίσκονται στα σημεία Κ και Λ της χορδής.
Τα υλικά σημεία Κ, Λ απέχουν μεταξύ τους απόσταση (ΚΛ)=0,2m. To κύμα κατά τη διάδοσή του περνάει πρώτα από το σημείο Κ και μετά από το σημείο Λ.
Θεωρούμε ως αρχή μέτρησης των αποστάσεων (x=0), τη θέση ισορροπίας του υλικού σημείου Κ και ως αρχή μέτρησης των χρόνων (t=0), τη χρονική στιγμή που το κύμα φτάνει για πρώτη φορά στο σημείο Κ. Tο σημείο Κ τη στιγμή αυτή
βρίσκεται στη θέση ισορροπίας του (y=0) και ξεκινά να κινείται προς τη θετική κατεύθυνση. Κατά τη διάρκεια της ταλάντωσης του υλικού σημείου Κ, η κινητική του ενέργεια μεγιστοποιείται κάθε 0,25sec. Παρατηρούμε ότι, μια χρονική στιγμή που το υλικό σημείο Λ βρίσκεται σε κορυφή κύματος (y=+Α), το υλικό σημείο Κ βρίσκεται και αυτό σε κορυφή κύματος ( y=+Α) και ανάμεσά τους υπάρχει ακόμα μια κορυφή κύματος (y=+Α). Η κατακόρυφη απόσταση μεταξύ των ακραίων θέσεων ταλάντωσης του υλικού σημείου Κ είναι 0,04m.
Γ1. Να υπολογίσετε τo μήκος κύματος λ, τη συχνότητα f και την ταχύτητα διάδοσής του κύματος. Μονάδες 6
Γ2. Να γράψετε την εξίσωση της ταχύτητας ταλάντωσης του υλικού σημείου Λ σε συνάρτηση με τον χρόνο και να κάνετε τη γραφική της παράσταση σε συνάρτηση με τον χρόνο, σε βαθμολογημένους άξονες από τη χρονική στιγμή t=0 έως τη χρονική στιγμή t1=1,75sec. Μονάδες 6
Αυξάνουμε τη συχνότητα ταλάντωσης της πηγής χωρίς να αλλάξει το πλάτος του κύματος.
Γ3. Να υπολογίσετε την αύξηση της συχνότητας Δf έτσι ώστε, όταν μια χρονική στιγμή τα υλικά σημεία Κ και Λ βρίσκονται σε κορυφές κυμάτων (y=+A), ανάμεσά τους να υπάρχουν συνολικά 3 κορυφές κύματος (y=+A). Μονάδες 6
Γ4. Aν Κmax,1 είναι η μέγιστη κινητική ενέργεια του υλικού σημείου Κ πριν την αλλαγή της συχνότητας f και Κmax, 2 η κινητική του ενέργεια μετά την αλλαγή της συχνότητας f, να υπολογίσετε την τιμή του λόγου Kmax,1 / Kmax,2. Μονάδες 7
Γ1. (ΚΛ) = 0,2 m T/2 = 0,25 s => T = 0,5 s f = 1/T = 2 Hz ω = 2π/Τ = 4π rad/s 2A = 0,04 m => A = 0,02 m 2λ = 0,2 m => λ = 0,1 m v = λ f = 0,2 m/s
y(K) = A ημ(ωt - 2π xK /λ ) = 0,02 ημ(4πt) xK = 0 xΛ = 0,2 m
Γ2. y(Λ) = A ημ(ωt - 2π xΛ /λ ) = 0,02 ημ(4πt - 2π 0,2 /0,1 ) =>
=> y(Λ) = 0,02 ημ(4πt - 4π) = 0,02 ημ(4πt) 1 s £ t £ 1,75 s
t = 1,75 s = 0,5 + 0,5 + 0,5 + 0,25 = 3T + T/2
Γ3. 4λ' = 0,2 m => λ' = 0,05 m λ' f ' = v => 0,05 m f ' = 0,2 m/s => f ' = 0,2 / 0,05 = 4 Hz Δf = f ' - f = 4 - 2 = 2 Hz
Γ4. y(Λ) = 0,02 ημ(4πt - 4π) = 0,02 ημ(4πt) v(Λ) = 0,08π συν(4πt - 4π) = 0,08π συν(4πt)
Kmax,1 = ½ Δm vmax,12 = ½ Δm (0,08π)2
f ' = 4 Hz ω' = 2π 4 = 8π rad/s y'(Λ) = A ημ(ω't - 2π xΛ /λ' ) = 0,02 ημ(8πt - 2π 0,2 /0,05 ) => y'(Λ) = 0,02 ημ(8πt - 8π) = 0,02 ημ(8πt) v'(Λ) = 0,16π ημ(8πt - 8π) = 0,16π ημ(8πt)
Kmax,2 = ½ Δm vmax,22 = ½ Δm (0,16π)2
Kmax,1 / Kmax,2 = (0,08π)2 / (0,16π)2 = 1/4
επαναληπτικές ΣΕΠ 2019
ΘΕΜΑ Γ
Γραμμικό ομογενές ελαστικό μέσο μεγάλου μήκους εκτείνεται κατά μήκος του θετικού ημιάξονα Οx. Στο σημείο Ο (στη θέση x=0) είναι τοποθετημένη σημειακή πηγή που εκτελεί αρμονική ταλάντωση με εξίσωση απομάκρυνσης της μορφής y=Α∙ημωt, με αποτέλεσμα να δημιουργείται ένα εγκάρσιο αρμονικό κύμα, το οποίο διαδίδεται χωρίς απώλειες ενέργειας προς τη θετική κατεύθυνση του άξονα Ox. Η γραφική παράσταση της φάσης φ σε συνάρτηση με το χρόνο t, για ένα σημείο Ρ του ελαστικού μέσου, το οποίο βρίσκεται στη θέση xP=1m, δίνεται από το σχήμα.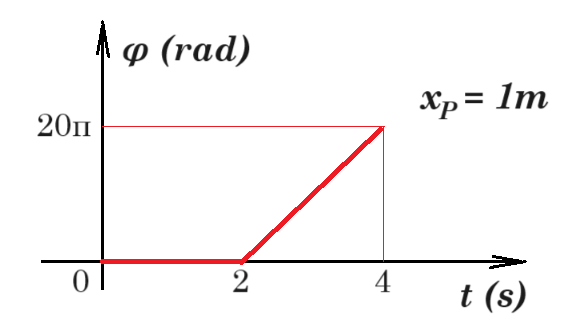
Η ενέργεια ταλάντωσης μιας στοιχειώδους μάζας Δm=2∙10-6 kg του ελαστικού μέσου είναι ίση με 16π2∙10-8 J.
Γ1. Να υπολογίσετε τo πλάτος ταλάντωσης Α της πηγής του κύματος . Μονάδες 6
Γ2. Να γράψετε την εξίσωση του αρμονικού κύματος στο διεθνές σύστημα μονάδων (SI). Μονάδες 6
Ένα σημείο Σ του ελαστικού μέσου βρίσκεται στη θέση xΣ=1,15m.
Γ3. Να υπολογίσετε το μέτρο της ταχύτητας του σημείου Σ (μονάδες 6) και την κατεύθυνσή της (μονάδα 1) τη χρονική στιγμή που το σημείο Ρ διέρχεται από τη θέση ισορροπίας του με θετική ταχύτητα. Μονάδες 7
Γ4. Να γράψετε την εξίσωση της απομάκρυνσης του σημείου Σ με το χρόνο, από τη χρονική στιγμή t=0 μέχρι τη χρονική στιγμή t1=2,7s (μονάδες 3) και να την σχεδιάσετε σε βαθμολογημένους άξονες (μονάδες 3). Μονάδες 6
Να μη γίνει αριθμητική αντικατάσταση του αριθμού π.
Γ1. φ = 10π (t - 2) = 10πt - 20π
φ = ωt - 2πx/λ => 10πt - 20π = ωt - 2π 1/λ => ω = 10π rad/s λ = 2π / 20π = 0,1 m
Ε = ½ Δm vmax2 => 16π2∙10-8 = ½ 2∙10-6 vmax2 => vmax = 0,4π m/s = ω Α = 10π Α => Α = 0,04 m
Γ2. y = 0,04 ημ(10πt - 20πx) ω = 10π rad/s T = 2π / ω = 0,2 s
Γ3. xΣ = 1,15 m
yΣ = 0,04 ημ(10πt - 20π 1,15) = 0,04 ημ(10πt - 23π) = 0,04 ημ(10πt - π) = - 0,04 ημ(10πt) vΣ = - 0,4π συν(10πt)
xΡ = 1 m
yΡ = 0,04 ημ(10πt - 20π 1) = 0,04 ημ(10πt - 20π) = 0,04 ημ(10πt) vΡ = 0,4π συν(10πt) yΡ = 0 => ημ(10πt) = 0 => συν(10πt) = 1 => vΡ = 0,4π m/s
yΣ = - 0,04 ημ(10πt) = 0 => vΣ = - 0,4π συν(10πt) = - 0,4π m/s
Γ4. xΣ = 1,15 m yΣ = 0,04 ημ(10πt - 23π) t > 2,3 s
2,7 s = 2,3 s + 0,4 s = 2,3 s + 2 T

επαναληπτικές ΣΕΠ 2017
B1. Δύο σώματα Σ1 και Σ2 με μάζες m και 4m αντίστοιχα έχουν ίσες κινητικές ενέργειες. Τα σώματα κινούνται σε αντίθετες κατευθύνσεις και συγκρούονται πλαστικά. Ο λόγος της τελικής κινητικής ενέργειας του συστήματος των
σωμάτων προς την αρχική κινητική ενέργεια του συστήματος των σωμάτων είναι ίσος με
i. 1/4 ii. 1/5 iii. 1/10
Κ1 = Κ2 => ½ m v12 = ½ 4m v22 => v1 = 2 v2
m v1 - 4m v2 = 5m u => m 2v2 - 4m v2 = 5m u => - 2 v2 = 5 u => u = - 2/5 v2
Kτελ = ½ 5m 4/25 v22 = 2/5 m v22 Καρχ = 2 ½ 4m v22 = 4m v22
Kτελ / Καρχ = 2/5 / 4/1 = 1/10 (iii)
ΘΕΜΑ Γ
Στην επιφάνεια ενός υγρού που ηρεμεί βρίσκονται δύο σύγχρονες και όμοιες σημειακές πηγές Π1 και Π2 που απέχουν μεταξύ τους απόσταση d. Οι πηγές αρχίζουν να ταλαντώνονται τη χρονική στιγμή t = 0 και εκτελούν ταλαντώσεις της
μορφής y = A ∙ ημωt δημιουργώντας στην επιφάνεια του υγρού εγκάρσια κύματα.
Ένα υλικό σημείο Σ της επιφάνειας του υγρού που απέχει αποστάσεις r1 = 1,4 m και r2 (r2 > r1) αντίστοιχα από τις πηγές Π1 και Π2 ταλαντώνεται και η απομάκρυνσή του από τη θέση ισορροπίας του σε συνάρτηση με τον χρόνο περιγράφεται από τη γραφική παράσταση του σχήματος. 
Γ1. Να υπολογίσετε την ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού (μονάδες 3) και την απόσταση r2 του σημείου Σ από την πηγή Π2. (μονάδες 3) Μονάδες 6
Γ2. Να υπολογίσετε τη συχνότητα ταλάντωσης των πηγών Π1 και Π2 (μονάδες 3) και το μήκος κύματος λ των εγκαρσίων κυμάτων που διαδίδονται στην επιφάνεια του υγρού. (μονάδες 3) Μονάδες 6
Γ3. Να υπολογίσετε την απομάκρυνση του σημείου Σ από τη θέση ισορροπίας τη χρονική στιγμή t = 5/8 s. Μονάδες 6
Γ4. Μεταβάλλουμε ταυτόχρονα, με τον ίδιο τρόπο, τη συχνότητα ταλάντωσης των δύο πηγών Π1 και Π2. Να υπολογίσετε την ελάχιστη συχνότητα ταλάντωσης των δύο πηγών Π1 και Π2 ώστε το σημείο Σ να παραμένει συνεχώς ακίνητο, μετά τη συμβολή των κυμάτων στο σημείο αυτό. Μονάδες 7
Γ1. v = r1 / t1 = 1,4m / 0,35s = 4 m/s r2 = v t2 = 4m/s 0,55s = 2,2 m
Γ2. T = (0,55s - 0,35s) / 2 = 0,1 s f = 1/T = 10 Hz λ = v / f = 0,4 m ω = 2πf = 20π ad/s
Γ3. y1 = 0,05 ημ(2πf t - 2πr1 /λ) = 0,05 ημ(20πt - 2π 1,4 / 0,4) = 0,05 ημ(20πt - 7π)
y2 = 0,05 ημ(2πf t - 2πr2 /λ) = 0,05 ημ(20πt - 2π 2,2 / 0,4) = 0,05 ημ(20πt - 11π)
5/8 s = 0,625 s > 0,55 s έχουν φθάσει και τα δύο κύματα στο σημείο Σ
y = 0,1 συν(11π - 7π)/2 ημ( 20πt - 18π/2 ) = 0,1 συν(2π) ημ(20πt - 9π) = 0,1 ημ(20πt - 9π) = y(t)
y(5/8) = 0,1 ημ(20π 5/8 - 9π) = 0,1 ημ(12π + π/2 - 9π) = 0,1 ημ(π/2 + 3π) = 0,1 ημ(3π/2) = - 0,1 m
y(t) = 0,1 ημ(20πt - 9π) => v(t) = 2π συν(20πt - 9π)
v(5/8) = 2π συν(20π 5/8 - 9π) = 2π συν(12π + π/2 - 9π) = 2π συν(3π/2) = 0
Γ4.
το σημείο Σ είναι ακίνητο r2 - r1 = Νλ' + λ'/2 =>Ν=0 2,2 - 1,4 = λ'/2 => λ' = 1,6 m
f ' = v / λ' = 4m/s / 1,6m = 2,5 Hz
επαναληπτικές ΣΕΠ 2016
Β2. Εγκάρσιο αρμονικό κύμα διαδίδεται χωρίς απώλειες ενέργειας σε γραμμικό ελαστικό μέσο που ταυτίζεται με τον
άξονα x ́Οx προς τη θετική κατεύθυνση.
Η πηγή του κύματος βρίσκεται στην αρχή Ο του άξονα x ́Οx και εκτελεί απλή αρμονική ταλάντωση με εξίσωση
y = Αημωt. 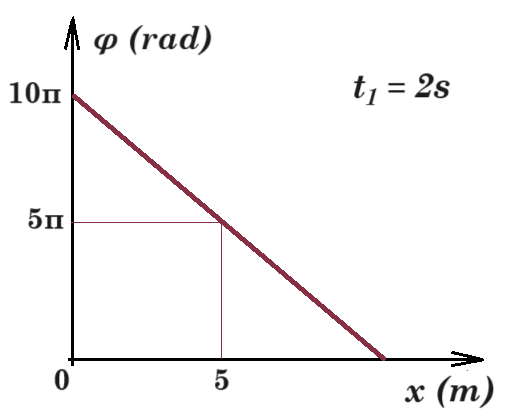
Στο διάγραμμα του σχήματος παριστάνεται η φάση των σημείων του ελαστικού μέσου σε συνάρτηση με την απόστασή τους x από την πηγή, τη χρονική στιγμή t1 = 2s. Η ταχύτητα διάδοσης του κύματος είναι ίση με:
i. υ = 0,8 m/s ii. υ = 5 m/s iii. υ = 12,5 m/s
φ = ωt - 2πx / λ φ = 10π - πx [0 , 10m]
10π rad = ω 2s => ω = 5π rad/s T = 2π/ω = 2π / 5π = 0,4 s
2π / λ = π => λ = 2 m v = λ / T = 2m /0,4s = 5 m/s (ii)
Θέμα Δ
Ομογενής δίσκος Σ1 έχει μάζα Μ1 = 8 kg και ακτίνα R1 = 0,2 m. Στο σημείο Β της κατακόρυφης διαμέτρου του δίσκου, που απέχει απόσταση d = 1,5 R1 από το οριζόντιο επίπεδο, είναι στερεωμένο οριζόντιο αβαρές μη εκτατό νήμα (1).
Το άλλο άκρο Α του νήματος (1) είναι ακλόνητα στερεωμένο, όπως φαίνεται στο σχήμα. Γύρω από την περιφέρεια του δίσκου Σ1 είναι τυλιγμένο πολλές φορές άλλο δεύτερο αβαρές μη εκτατό νήμα (2), το οποίο διέρχεται από τροχαλία Σ2, μάζας Μ2 = 2 kg και ακτίνας R2 = 0,1 m. Στο άλλο άκρο του νήματος (2) είναι συνδεδεμένο σώμα Σ3, μάζας Μ3 = 1 kg. Το σύστημα αρχικά ισορροπεί. Το τμήμα ΓΔ του νήματος (2) είναι οριζόντιο.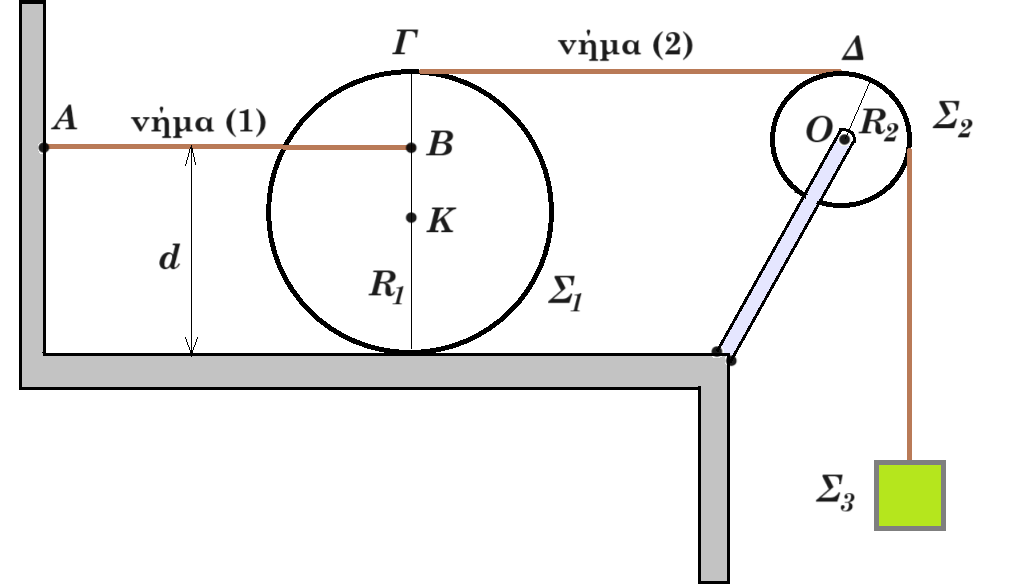
Δ1. Να υπολογίσετε την τάση του νήματος στο σημείο Α από τον δίσκο Σ1. Μονάδες 6
Τη χρονική στιγμή t0 = 0 το νήμα (1) κόβεται. Το σώμα Σ3 κατέρχεται με επιτάχυνση. Η τροχαλία Σ2 αρχίζει να περιστρέφεται, χωρίς τριβές, γύρω από τον άξονά της και ο δίσκος Σ1 αρχίζει να κυλίεται, χωρίς να ολισθαίνει, πάνω στο οριζόντιο επίπεδο.
Δ2. Να υπολογίσετε το μέτρο της επιτάχυνσης του κέντρου μάζας του δίσκου Σ1. Μονάδες 10
Δ3. Να υπολογίσετε το μέτρο της στροφορμής της τροχαλίας Σ2 τη χρονική στιγμή t1 = 1s. Μονάδες 5
Δ4. Να υπολογίσετε τη μεταβολή της βαρυτικής δυναμικής ενέργειας του σώματος Σ3 για την κίνηση του από τη χρονική στιγμή t0 = 0 έως τη χρονική στιγμή t1 = 1s.
Να θεωρήσετε ότι :
α) η τριβή του νήματος (2) τόσο με το δίσκο Σ1, όσο και με την τροχαλία Σ2, είναι αρκετά μεγάλη ώστε να μην παρατηρείται ολίσθηση.
β) κατά τη διάρκεια όλου του φαινομένου, ο δίσκος παραμένει στο οριζόντιο επίπεδο, χωρίς να συγκρούεται με την τροχαλία.
γ) ο άξονας περιστροφής του δίσκου δεν αλλάζει κατεύθυνση, κατά τη διάρκεια της κίνησής του.
δ) το σώμα Σ3 έχει αμελητέες διαστάσεις.
ε) η αντίσταση του αέρα είναι αμελητέα.
Δ1. ισορροπία Σ3 : Μ3 g = T3 => T3 = 10 N
ισορροπία Σ2 : Στ(Ο) = 0 => T2 R2 = T3 R2 => T2 = T3 = 10 N
ΣFx = 0 => F(O),x = T2 = 10 N
ΣFy = 0 => F(O),y - M2 g - T3 = 0 => F(O),y - 20 - 10 = 0 => F(O),y = 30 N
F(O)2 = F(O),x2 + F(O),y2 = 100 + 900 = 1000 => F(O) = 1010 N
ισορροπία Σ1 : Στ(Ζ) = 0 => T2 2R1 = T1 3/2 R1 => T1 = 4/3 T2 = 40/3 N => T1 = 40/3 N
άρα υπάρχει ύναμη τριβής στο σημείο Ζ έστω Ττρ
ΣFx = 0 => T2 - T1 + Ττρ = 0 => 10 - 40/3 + Ττρ = 0 => Ττρ = 10/3 N οριζόντια δεξιά
ΣFy = 0 => N = M1 g = 80 Newton συντελεστής στατικής τριβής : μ = Ττρ / Ν = 10/3 / 80 = 1/24
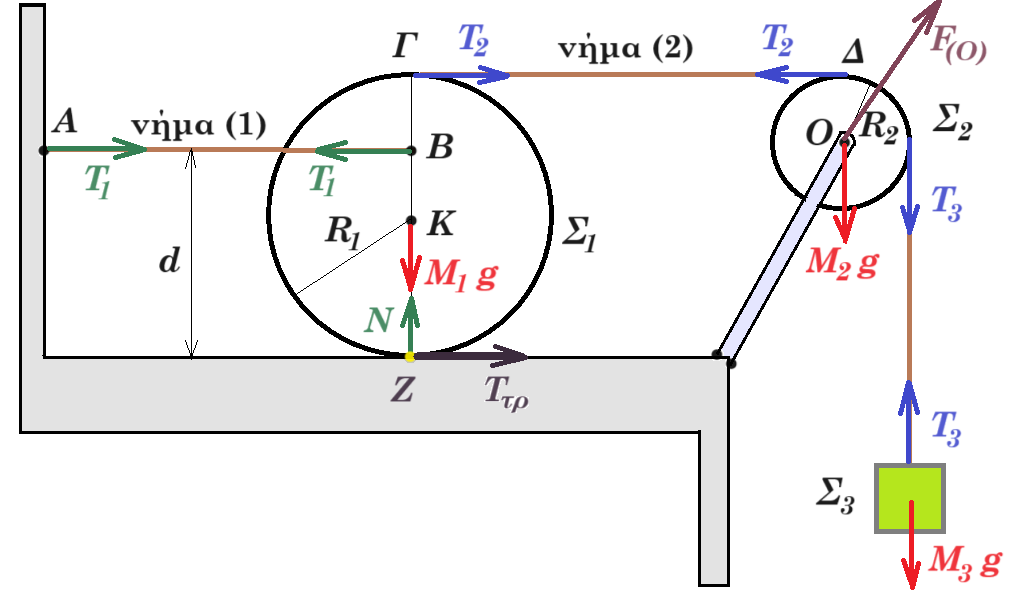
Δ2. το Σ3 κατέρχεται επιταχυνόμενο : Μ3 g - T3 = Μ3 α3 => 10 - Τ3 = 1 α3 => 10 - Τ3 = α3 (1)
η τροχαλία Σ2 περιστρέφεται με γωνιακή επιτάχυνση αγων,2 = α3 / R2
T3 R2 - T2 R2 = ½ M2 R22 αγων,2 => T3 - T2 = ½ M2 R2 αγων,2 => T3 - T2 = a3 (2)
ο δίσκος κυλίεται χωρίς να ολισθαίνει : Τ2 + Ττρ = Μ1 αcm,1 (3) T2 R1 - Tτρ R1 = ½ M1 R12 αγων,1 => T2 - Tτρ = ½ M1 R1 αγων,1 => T2 - Tτρ = ½ M1 αcm,1 (4)
(3) + (4) => 2 Τ2 = 3/2 Μ1 αcm,1 => Τ2 = 3/4 8 αcm,1 = 6 αcm,1 (5)
a3 = αγων,2 R2 = aΔ = αΓ = 2 αcm,1 (6)
(1) + (2) + (5) => 10 = 2 α3 + 6 αcm,1 => 10 = 4 αcm,1 + 6 αcm,1 => αcm,1 = 1 m/s2 a3 = 2 m/s2
αγων,1 = αcm,1 / R1 = 1 / 0,2 = 5 rad/s2 αγων,2 = α3 / R2 = 2 / 0,1 = 20 rad/s2
(1) => 10 - Τ3 = 2 => Τ3 = 8 Ν (2) => 8 - Τ2 = 2 => Τ2 = 6 Ν (3) => 6 + Ττρ = 8 => Ττρ = 2 Ν

Δ3. L2 = ½ M2 R22 αγων,2 t = ½ 2 0,12 20 1 = 0,2 kg m2/s
Δ4. h = 0,5 a3 t2 = 0,5 2 1 = 1 m v = a3 t = 2 m/s2 1 s = 2 m/s
ΔU = - m3 g h = - 1 kg 10 m/s2 1 m = - 10 J μεταβολή δυναμικής βαρυτικής ενέργειας του Σ3
dU/dt = - m3 g v = - 1 kg 10 m/s2 2 m/s = - 20 J/s ρυθμός μεταβολής δυναμικής βαρυτικής ενέργειας του Σ3
Θέμα Δ τροποποίηση
Ομογενής δίσκος Σ1 έχει μάζα Μ1 = 8 kg και ακτίνα R1 = 0,2 m. Στο σημείο Β της κατακόρυφης διαμέτρου του δίσκου, που απέχει απόσταση d = 1,5 R1 από το οριζόντιο επίπεδο, είναι στερεωμένο οριζόντιο αβαρές μη εκτατό νήμα (1).
Το άλλο άκρο Α του νήματος (1) είναι ακλόνητα στερεωμένο, όπως φαίνεται στο σχήμα. Γύρω από την περιφέρεια του δίσκου Σ1 είναι τυλιγμένο πολλές φορές άλλο δεύτερο αβαρές μη εκτατό νήμα (2), το οποίο διέρχεται από τροχαλία Σ2, μάζας Μ2 = 2 kg και ακτίνας R2 = 0,1 m. Στο άλλο άκρο του νήματος (2) είναι συνδεδεμένο σώμα Σ3, μάζας Μ3 = 1 kg. Το σύστημα αρχικά ισορροπεί. Το τμήμα ΓΔ του νήματος (2) είναι οριζόντιο.
Δ1. Να υπολογίσετε τις δυνάμεις που ασκούνται στον δίσκο Σ1 και στον δίσκο Σ2. Μονάδες 10
Τη χρονική στιγμή t0 = 0 το νήμα (1) κόβεται. Το σώμα Σ3 κατέρχεται με επιτάχυνση. Η τροχαλία Σ2 αρχίζει να περιστρέφεται, χωρίς τριβές, γύρω από τον άξονά της και ο δίσκος Σ1 αρχίζει να κυλίεται, χωρίς να ολισθαίνει, πάνω στο οριζόντιο επίπεδο έχοντας γωνιακή επιτάχυνση αγων,1 = + 5 rad/s2.
Δ2. Να υπολογίσετε την γωνιακή επιτάχυνση αγων,2 της τροχαλίας Σ2. Μονάδες 5
Δ3. Να υπολογίσετε την στροφορμή του Σ3 ως προς το Ο τη χρονική στιγμή t1 = 1s. Μονάδες 5
Δ4. Να υπολογίσετε τη μεταβολή της βαρυτικής δυναμικής ενέργειας του σώματος Σ3 για την κίνηση του από τη χρονική στιγμή t0 = 0 έως τη χρονική στιγμή t1 = 1s. Μονάδες 5
Να θεωρήσετε ότι :
α) η τριβή του νήματος (2) τόσο με το δίσκο Σ1, όσο και με την τροχαλία Σ2, είναι αρκετά μεγάλη ώστε να μην παρατηρείται ολίσθηση.
β) κατά τη διάρκεια όλου του φαινομένου, ο δίσκος παραμένει στο οριζόντιο επίπεδο, χωρίς να συγκρούεται με την τροχαλία.
γ) ο άξονας περιστροφής του δίσκου δεν αλλάζει κατεύθυνση, κατά τη διάρκεια της κίνησής του.
δ) το σώμα Σ3 έχει αμελητέες διαστάσεις.
ε) η αντίσταση του αέρα είναι αμελητέα.
Δ1. ισορροπία Σ3 : Μ3 g = T3 => T3 = 10 N
ισορροπία Σ2 : Στ(Ο) = 0 => T2 R2 = T3 R2 => T2 = T3 = 10 N
ΣFx = 0 => F(O),x = T2 = 10 N
ΣFy = 0 => F(O),y - M2 g - T3 = 0 => F(O),y - 20 - 10 = 0 => F(O),y = 30 N
F(O)2 = F(O),x2 + F(O),y2 = 100 + 900 = 1000 => F(O) = 1010 N
ισορροπία Σ1 : Στ(Ζ) = 0 => T2 2R1 = T1 3/2 R1 => T1 = 4/3 T2 = 40/3 N => T1 = 40/3 N
άρα υπάρχει ύναμη τριβής στο σημείο Ζ έστω Ττρ
ΣFx = 0 => T2 - T1 + Ττρ = 0 => 10 - 40/3 + Ττρ = 0 => Ττρ = 10/3 N οριζόντια δεξιά
ΣFy = 0 => N = M1 g = 80 Newton συντελεστής στατικής τριβής : μ = Ττρ / Ν = 10/3 / 80 = 1/24

Δ2. το Σ3 κατέρχεται επιταχυνόμενο : Μ3 g - T3 = Μ3 α3 => 10 - Τ3 = 1 α3 => 10 - Τ3 = α3 (1)
η τροχαλία Σ2 περιστρέφεται με γωνιακή επιτάχυνση αγων,2 = α3 / R2
T3 R2 - T2 R2 = ½ M2 R22 αγων,2 => T3 - T2 = ½ M2 R2 αγων,2 => T3 - T2 = a3 (2)
ο δίσκος κυλίεται χωρίς να ολισθαίνει : Τ2 + Ττρ = Μ1 αcm,1 (3) T2 R1 - Tτρ R1 = ½ M1 R12 αγων,1 => T2 - Tτρ = ½ M1 R1 αγων,1 => T2 - Tτρ = ½ M1 αcm,1 (4)
(3) + (4) => 2 Τ2 = 3/2 Μ1 αcm,1 => Τ2 = 3/4 8 αcm,1 = 6 αcm,1 (5)
a3 = αγων,2 R2 = aΔ = αΓ = 2 αcm,1 (6)
(1) + (2) + (5) => 10 = 2 α3 + 6 αcm,1 => 10 = 4 αcm,1 + 6 αcm,1 => αcm,1 = 1 m/s2 a3 = 2 m/s2
αcm,1 = αγων,1 R1 = 5 rad/s2 0,2 m = 1 m/s2 a3 = 2αcm,1 = 2 m/s2
αγων,2 = α3 / R2 = 2 / 0,1 = 20 rad/s2
(1) => 10 - Τ3 = 2 => Τ3 = 8 Ν (2) => 8 - Τ2 = 2 => Τ2 = 6 Ν (3) => 6 + Ττρ = 8 => Ττρ = 2 Ν

Δ3. L3 = M3 R2 υ = M3 R2 α3 t = 1 0,1 2 1 = 0,2 kg m2/s
Δ4. h = 0,5 a3 t2 = 0,5 2 1 = 1 m v = a3 t = 2 m/s2 1 s = 2 m/s
ΔU = - m3 g h = - 1 kg 10 m/s2 1 m = - 10 J μεταβολή δυναμικής βαρυτικής ενέργειας του Σ3
dU/dt = - m3 g v = - 1 kg 10 m/s2 2 m/s = - 20 J/s ρυθμός μεταβολής δυναμικής βαρυτικής ενέργειας του Σ3
επαναληπτικές ΣΕΠ 2015
Β1. Δύο σώματα αμελητέων διαστάσεων με μάζες m1 και m2 συγκρούονται κεντρικά σε λείο οριζόντιο επίπεδο. Η θέση x κάθε σώματος στην ευθεία γραμμή, που τα ενώνει, μετριέται από κοινή αρχή. Η γραφική παράσταση της θέσης των σωμάτων φαίνεται στο σχήμα. Δίνεται ότι η διάρκεια της επαφής των δύο σωμάτων κατά την κεντρική κρούση είναι αμελητέα. Η κρούση των δύο σωμάτων είναι : i. ελαστική ii. ανελαστική iii. πλαστική.
Το σώμα Σ2 συνδέεται με το ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k = 150 N/m του οποίου το άλλο άκρο είναι ακλόνητο σε σημείο Α τοίχου. Εάν m1 = 1kg εκφράστε την δύναμη του ελατηρίου στο άκρο Α και τον ρυθμό μεταβολής της κινητικής ενέργειας του σώματος Σ2.
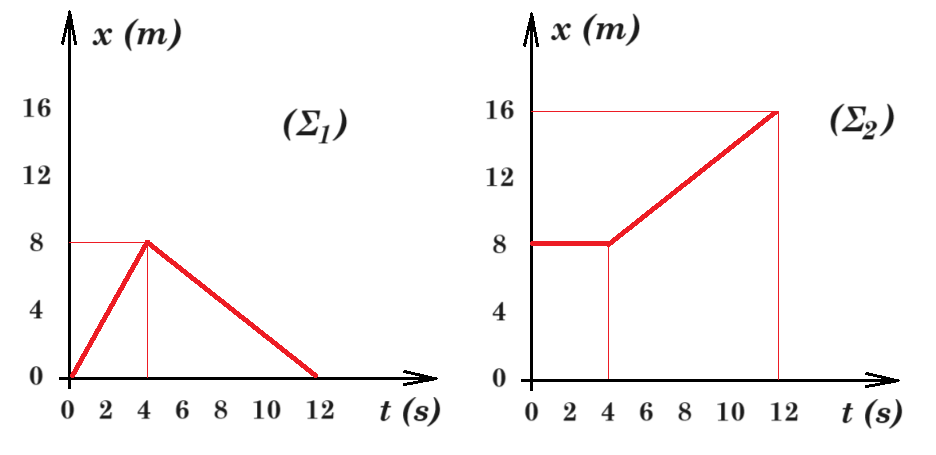
από 0 έως 4s το Σ1 κινείται προς τα δεξιά με ταχύτητα v1 = 8m / 4s = 2 m/s ενώ το Σ2 είναι ακίνητο άρα ισορροπεί στο άκρο του ελατηρίου άρα το ελατήριο έχει το φυσικό του μήκος
από 4s έως 12s το Σ1 κινείται με ταχύτητα v1' = - 8m / (12s - 4s) = - 1 m/s (προς τα αριστερά) ενώ το Σ2 κινείται με ταχύτητα v2' = (16m - 8m) / (12s - 4s) = + 1 m/s (προς τα δεξιά)
διατήρηση ορμής κατά την κρούση : m1 v1 = m1 v1' + m2 v2' => m1 2 m/s = m1 (- 1 m/s) + m2 1 m/s => m2 = 3 m1
Κτελ = ½ m1 (v1')2 + ½ m2 (v2')2 = ½ m1 1 + ½ 3m1 1 = 2m1
Καρχ = ½ m1 v12 = ½ m1 22 = 2m1 Καρχ = Κτελ ελαστική κρούση
μετά την κρούση το Σ2 κινείται προς τα δεξιά με ταχύτητα 1 m/s όπου βρίσκεται το ελατήριο και το συσπειρώνει η μέγιστη συσπείρωση του ελατηρίου είναι : ½ m2 (v2')2 = ½ k A2 => 3 1 = 300 A2 => A = 0,1 m είναι το πλάτος ταλάντωσης του Σ2
k = m2 ω2 => 300 = 3 ω2 => ω = 10 rad/s
x(t) = 0,1 ημ(10t) v(t) = 1 συν(10t) a(t) = - 10 ημ(10t)
ΣF = m2 a = 3 ( - 10 ημ(10t) ) = - 30 ημ(10t) = - 300 x = Fελατ ασκείται στο σώμα Σ2
στο άλλο άκρο του ελατηρίου το Α ασκείται δύναμη ελατηρίου : Fελατ' = + 30 ημ(10t) = + 300 x
dK/dt = m2 v a = 3 1 συν(10t) ( - 10 ημ(10t) ) = - 30 ημ(10t) συν(10t) = - 15 ημ(20t)
Α3. Στο στιγμιότυπο αρμονικού μηχανικού κύματος του σχήματος παριστάνονται οι ταχύτητες ταλάντωσης δύο σημείων του. Το κύμα
α. διαδίδεται προς τα αριστερά
β. διαδίδεται προς τα δεξιά
γ. είναι στάσιμο
δ. μπορεί να διαδίδεται και προς τις δύο κατευθύνσεις (δεξιά ή αριστερά).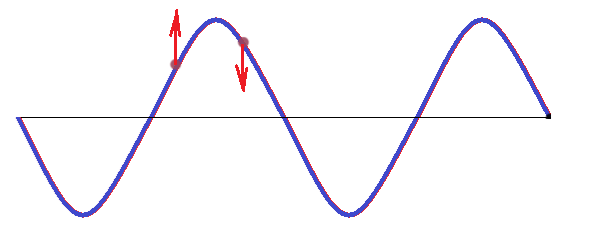
(α) το αριστερο σημείο ανεβαίνει το δεξιό κατεβαίνει αν μετακινηθεί το σχέδιο δεξιά δεν συμβαίνει αυτό
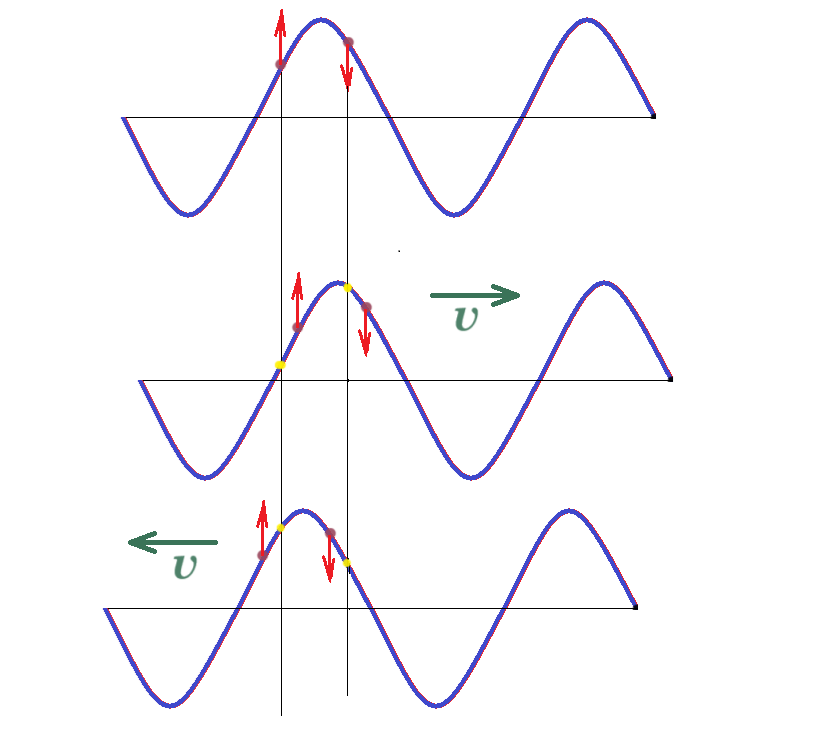
επαναληπτικές ΣΕΠ 2014

ΘΕΜΑ Γ
Τα σώματα Σ1 και Σ2, του σχήματος, με μάζες m1 = 1 kg και m2 = 4 kg αντίστοιχα, βρίσκονται ακίνητα σε λείο οριζόντιο επίπεδο και εφάπτονται μεταξύ τους όπως στο σχήμα 1. Τα σώματα είναι δεμένα στην άκρη δύο όμοιων ιδανικών ελατηρίων σταθεράς k = 100 Ν/m, που βρίσκονται στο φυσικό τους μήκος και των οποίων η άλλη άκρη είναι σταθερά στερεωμένη.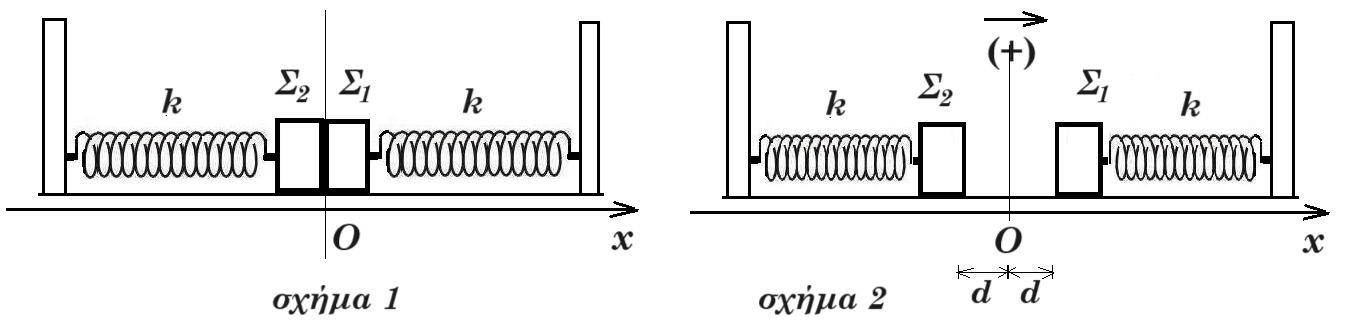
Μετακινούμε τα σώματα Σ1 και Σ2 έτσι ώστε τα ελατήρια να συσπειρωθούν κατά d = 0,2 m το καθένα όπως στο σχήμα 2 και στη συνέχεια τη χρονική στιγμή t = 0 αφήνονται ελεύθερα να ταλαντωθούν.
Γ1. Να γράψετε τις εξισώσεις των απομακρύνσεων x1 και x2 των σωμάτων Σ1 και Σ2 συναρτήσει του χρόνου. Ως θετική φορά ορίζεται η από το Σ2 προς Σ1 και ως x = 0 ορίζεται η θέση που εφάπτονται αρχικά τα σώματα. Μονάδες 6
Γ2. Τα σώματα Σ1 και Σ2 κινούμενα με αντίθετη φορά συγκρούονται στη θέση x = - d/2. Να υπολογίσετε τα μέτρα των ταχυτήτων τους ελάχιστα πριν από την κρούση. Μονάδες 6
Γ3. Η κρούση που ακολουθεί είναι πλαστική. Να αποδείξετε ότι το συσσωμάτωμα μετά την κρούση θα εκτελέσει απλή αρμονική ταλάντωση. Μονάδες 6
Γ4. Να βρείτε το μέτρο του μέγιστου ρυθμού μεταβολής της ορμής του συσσωματώματος μετά την κρούση. Μονάδες 7
Γ1. k = m1 ω12 => 100 = 1 ω12 => ω1 = 10 rad/s T1 = 2π/ω1 = 2π/10 = π/5 s f1 = 1/T1 = 5/π Hz
k = m2 ω22 => 100 = 4 ω22 => ω2 = 5 rad/s T2 = 2π/ω2 = 2π/5 s f2 = 1/T2 = 5/2π Hz
x1 = 0,2 ημ(10t + π/2) v1 = 2 συν(10t + π/2) a1 = - 20 ημ(10t + π/2)
x2 = 0,2 ημ(5t + 3π/2) v2 = 1 συν(5t + 3π/2) a2 = - 5 ημ(5t + 3π/2)
Γ2. x1 = 0,2 ημ(10t + π/2) = - 0,1 => ημ(10t + π/2) = - 0,5 συν(10t + π/2) = - √3/2 το Σ1 κινείται προς τα αριστερά v1 = 2 συν(10t + π/2) = - √3 m/s
x2 = 0,2 ημ(5t + 3π/2) = - 0,1 => ημ(5t + 3π/2) = - 0,5 συν(5t + 3π/2) = + √3/2 το Σ2 κινείται προς τα δεξιά v2 = 1 συν(5t + 3π/2) = + √3/2 m/s
Γ3. m1 v1 + m2 v2 = (m1 + m2) u => 1 ( - √3 ) + 4 ( + √3/2 ) = 5 u => u = +√3/5 m/s
το συσσωμάτωμα συνδέεται με δύο ελατήρια ΣF = - k x - k x = - 2k x
η σταθερά ταλάντωσης D = 2k = 200 N/m
D = (m1 + m2) ω'2 => 200 = 5 ω'2 => ω' = √40 rad/s = 2√10 rad/s
η θέση ισορροπίας είναι όπου το φυσικό μήκος των ελατηρίων
διατήρηση ενέργειας για την ταλάντωση : 0,5 200 A2 = 0,5 5 (+√3/5)2 + 0,5 200 (-0,1)2 =>
200 A2 = 3/5 + 2 = 13/5 => A2 = 13/1000 = 0,013 => A = 0,1√1,3 m
Γ4. x = Α ημ(ω't + φ) = 0,1√1,3 ημ(2√10t + φ)
t = 0 x = - 0,1 m - 0,1 = 0,1√1,3 ημ(φ) => ημ(φ) = - 1/√1,3
το συσσωμάτωμα κινείται προς τα δεξιά συν(φ) = + √(1 - 1/1,3) = + √(3/13)
x = 0,1√1,3 ημ(2√10t + φ) v = 0,2√13 συν(2√10t + φ) α = - 0,4√130 ημ(2√10t + φ)
dp/dt = ΣF = (m1 + m2) a = - 2√130 ημ(2√10t + φ) = - 200 x
dp/dtmax = 200 A = 200 0,1√1,3 = 2√130 N
επαναληπτικές ΣΕΠ 2013
ΘΕΜΑ Α
Στις ημιτελείς προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά.
Α1. Σε μία απλή αρμονική ταλάντωση η ταχύτητα του σώματος που ταλαντώνεται δίνεται από τη σχέση υ = Aωημωt . Τότε η απομάκρυνση x από τη θέση ισορροπίας δίνεται από τη σχέση:
α. x = Aημωt
β. x = Aσυνωt
γ. x = Aημ(ωt+π)
δ. x = Aημ(ωt+3π/2) . Μονάδες 5
Α3. Σε μια φθίνουσα ταλάντωση η δύναμη που προκαλεί την απόσβεση είναι της μορφής F = -bυ , όπου b θετική σταθερά και υ η ταχύτητα του σώματος που ταλαντώνεται. Το έργο της δύναμης αυτής είναι
α. θετικό, όταν το σώμα κινείται προς την αρνητική κατεύθυνση
β. πάντα αρνητικό .
γ. πάντα θετικό
δ. μηδέν για μια πλήρη ταλάντωση Μονάδες 5
επαναληπτικές ΣΕΠ 2011
Β3. Τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από ακλόνητο οριζόντιο άξονα που περνά από το κέντρο
μάζας της. Γύρω από την τροχαλία είναι τυλιγμένο αβαρές και μη εκτατό νήμα.
Όταν στο ελεύθερο άκρο του νήματος ασκούμε κατακόρυφη δύναμη με φορά προς τα κάτω μέτρου F, η τροχαλία αποκτά γωνιακή επιτάχυνση μέτρου αγων,1 ενώ, όταν κρεμάμε στο ελεύθερο άκρο του νήματος σώμα βάρους w = F η τροχαλία αποκτά γωνιακή επιτάχυνση αγων,2. Ισχύει:
α. αγων,1 = αγων,2, β. αγων,1 > αγων,2, γ. αγων,1 < αγων,2.
Να επιλέξετε τη σωστή απάντηση. (μονάδες 2)
Να δικαιολογήσετε την επιλογή σας. (μονάδες 7)
Θέμα Δ
Λεία οριζόντια σανίδα μήκους L = 3 m και μάζας Μ = 0,4 Kg αρθρώνεται στο άκρο της Α σε κατακόρυφο τοίχο. Σε απόσταση d = 1 m από τον τοίχο, η σανίδα στηρίζεται ώστε να διατηρείται οριζόντια. Ιδανικό αβαρές ελατήριο σταθεράς k = 100 Ν/m συνδέεται με το ένα άκρο του στον τοίχο και το άλλο σε σώμα Σ1 μάζας m1= 1 Kg. Το ελατήριο βρίσκεται στο φυσικό του μήκος, ο άξονάς του είναι οριζόντιος και διέρχεται από το κέντρο μάζας του σώματος Σ1. Το κέντρο μάζας του σώματος Σ1 βρίσκεται σε απόσταση d από τον τοίχο.
Στη συνέχεια, ασκούμε στο σώμα Σ1 σταθερή οριζόντια δύναμη μέτρου F = 40 N με κατεύθυνση προς το άλλο άκρο Γ της σανίδας. Όταν το σώμα Σ1 διανύσει απόσταση s = 5 cm, η δύναμη παύει να ασκείται στο σώμα και, στη συνέχεια, το σώμα εκτελεί απλή αρμονική ταλάντωση.
Δ1) Να υπολογίσετε το πλάτος της απλής αρμονικής ταλάντωσης που θα εκτελέσει το σώμα Σ1.
Δ2) Να εκφράσετε το μέτρο της δύναμης FA που δέχεται η σανίδα από τον τοίχο σε συνάρτηση με την απομάκρυνση του σώματος Σ1 και να σχεδιάσετε την αντίστοιχη γραφική παράσταση.
Κατά μήκος της σανίδας από το άκρο Γ κινείται σώμα Σ2 μάζας m2= 1 Kg με ταχύτητα υ2= 2√3 m/s. Τα δύο σώματα συγκρούονται κεντρικά και ελαστικά, όταν η απομάκρυνση του σώματος Σ1είναι x1, όπου x1≥ 0. Το σώμα Σ1 μετά την
κρούση ταλαντώνεται με το μέγιστο δυνατό πλάτος.
Δ3) Να βρείτε την απομάκρυνση x1.
Δ4) Να βρείτε μετά από πόσο χρονικό διάστημα από τη στιγμή της κρούσης τα δύο σώματα θα συγκρουστούν για δεύτερη φορά.
Θεωρούμε θετική τη φορά της απομάκρυνσης προς το Γ.
Τριβές στην άρθρωση και στο υποστήριγμα δεν υπάρχουν.
∆ίνεται: επιτάχυνση βαρύτητας g = 10m/s2.
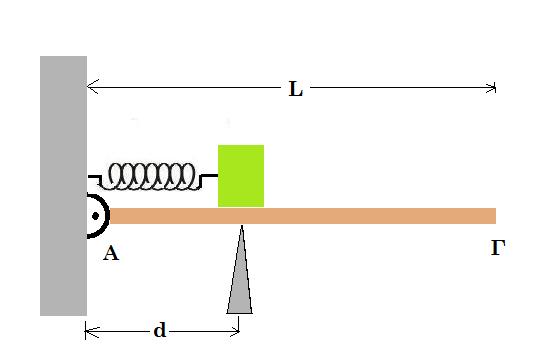
(Δ1) η δύναμη παράγει έργο συνεπώς το σώμα αποκτά κινητική ενέργεια και το ελατήριο δυναμική ενέργεια
WF = K + U = Kmax = Umax => F . s = 40 N . 0,05 m = 2 J = 0,5 . k . A2 = 0,5 . 100 Ν/m . A2 => A2 = 0,04 => A = 0,2 m το σώμα θα εκτελέσει ταλάντωση με πλάτος A = 0,2 m
(Δ2) έστω x προς το άκρο Γ είναι η απομάκρυνση του σώματος από τη θέση ισορροπίας, η σανίδα μένει σε οριζόντια θέση παίρνουμε ροπές ως προς το στήριγμα :
Μ g (L/2 - d) + m g x + FA d = 0 => 0,4 10 (3/2 - 1) + 1 10 x + FA 1 = 0 =>
=> 2 + 10 x + FA = 0 => FA = - 2 - 10x (S.I.) - 0,2 m £ x £ + 0,2 m διεύθυνση κατακόρυφη
(Δ3) το Σ1 απέχει x1 από τη Θ.Ι. έχει ταχύτητα υ1 : ½ k A2 = ½ k x12 + ½ m υ12 =>
=> ½ 100 0,22 = ½ 100 x12 + ½ 1 υ12 => 4 = 100 x12 + υ12 (1)
κεντρική - ελαστική κρούση το Σ2 κινείται προς τα αριστερά : υ1' = (m1 - m2) / (m1 + m2) υ1 + 2 m2 υ2 / (m1+ m2) =
= 2 1 (- 2√3) / 2 = - 2√3 m/s επειδή τα σώματα έχουν ίσες μάζες κατά την κρούση ανταλλάσουν ταχύτητες, τότε το Σ2 ακινητοποιείται ενώ το Σ1 κινείται προς τα αριστερά προς το Α και ταλαντώνεται με μέγιστο πλάτος Α' :
½ k (A')2 = ½ k x12 + ½ m (υ1')2 => ½ 100 (A')2 = ½ 100 x12 + ½ 1 (2√3 )2 =>
=> 100 (A')2 = 100 x12 + 12 (2) για να είναι το Α' μέγιστο πρέπει το x1 να είναι μέγιστο δηλαδή x1 = + 0,2 m
οπότε (2) => 100 (A')2 = 100 x12 + 12 => 100 (A')2 = 100 0,22 + 12 => 100 (A')2 = 4 + 12 = 16 => Α' = 0,4 m
(Δ4) το Σ1 μετά την κρούση θα κινηθεί προς το άκρο Α με ταχύτητα μέτρου υ1' = 2√3 m/s ενώ είναι σε απομάκρυνση x1 = + 0,2 m
ω2 = k / m1 = 100 / 1 => ω = 10 rad/s = 2π / Τ => Τ = π/5 s
x(t) = 0,4 ημ(10t + θ) x(0) = 0,4 ημ(θ) = +0,2 => ημ(θ) = +½
το Σ1 θέλει χρόνο Τ/12 για να πάει από τη θέση +Α/2 στη Θ.Ι. , χρόνο Τ/2 από τη Θ.Ι. στη θέση -Α και να επιστρέψει στη Θ.Ι. και χρόνο Τ/12 από τη Θ.Ι. να πάει στη θέση +Α/2
συνολικά Τ/12 + Τ/2 + Τ/12 = 2Τ/3 = 2/3 π/5 = 2π/15 s
επαναληπτικές ΣΕΠ 2009
ΘΕΜΑ 4ο
Στην επιφάνεια ενός ομογενούς κυλίνδρου μάζας Μ = 40 kg και ακτίνας R = 0,2 m, έχουμε τυλίξει λεπτό σχοινί αμελητέας μάζας, το ελεύθερο άκρο του οποίου έλκεται με σταθερή δύναμη F παράλληλη προς την επιφάνεια κεκλιμένου επιπέδου γωνίας κλίσεως 30°, όπως φαίνεται στο σχήμα.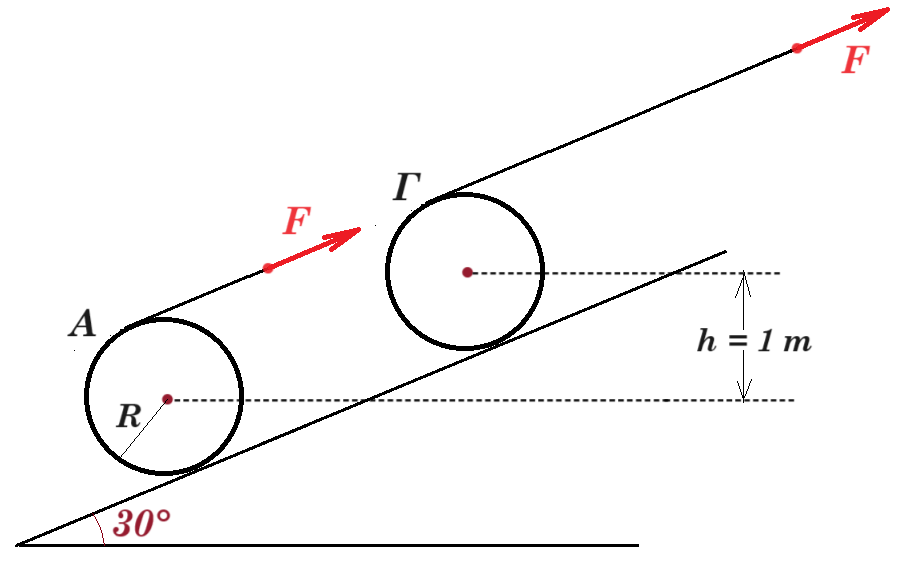
Το σχοινί ξετυλίγεται χωρίς ολίσθηση, περιστρέφοντας ταυτόχρονα τον κύλινδρο. Ο κύλινδρος κυλίεται πάνω στην επιφάνεια του κεκλιμένου επιπέδου χωρίς ολίσθηση.
α. Να υπολογισθεί το μέτρο της δύναμης F, ώστε ο κύλινδρος να ανεβαίνει στο κεκλιμένο επίπεδο με σταθερή ταχύτητα. Μονάδες 5
Αν αρχικά ο κύλινδρος είναι ακίνητος με το κέντρο μάζας του στη θέση Α και στο ελεύθερο άκρο του σχοινιού ασκηθεί σταθερή δύναμη F = 130N, όπως στο σχήμα:
β. Να υπολογισθεί η επιτάχυνση του κέντρου μάζας του κυλίνδρου. Μονάδες 6
γ. Να υπολογισθεί το μέτρο της στροφορμής του κυλίνδρου ως προς τον άξονα περιστροφής του όταν το κέντρο μάζας του περνάει από τη θέση Γ του σχήματος, η οποία βρίσκεται h = 1m ψηλότερα από τη θέση Α. Μονάδες 7
δ. Να υπολογισθεί το έργο της δύναμης F κατά τη μετακίνηση του κέντρου μάζας του κυλίνδρου από τη θέση Α στη θέση Γ και να δείξετε ότι αυτό ισούται με τη μεταβολή της μηχανικής ενέργειας του κυλίνδρου κατά τη μετακίνηση αυτή. Μονάδες 7
επιτάχυνση βαρύτητας g = 10m/s2.
4a) ο κύλινδρος ανεβαίνει με σταθερή ταχύτητα υ = σταθερή ω = σταθερή άρα αcm = 0 και αγων = 0
F R - T R = ½ M R2 αγων => F - T = 0 => F = T
F + T - Mg ημ30° = Μ αcm = 0 => F + T - ½ Mg = 0 => 2F = ½ 40 10 => F = 100 N
4β)
F R - T R = ½ M R2 αγων => F - T = ½ M R αγων = ½ M αcm (1)
F + T - Mg ημ30° = Μ αcm => F + T - ½ Mg = Μ αcm (2)
(1) + (2) => 2F - ½ Mg = Μ αcm + ½ M αcm => 2F - ½ Mg = 3/2 M αcm =>
=> 260 - ½ 400 = 3/2 40 αcm => 60 = 60 acm => acm = 1 m/s2
αγων = acm / R = 1 / 0,2 => αγων = 5 rad/s2
4γ)
(AΓ) = h / ημ30° = 1m / 0,5 = 2 m = 0,5 acm t2 => t2 = 4 => t = 2 s vcm = acm t = 2 m/s
vcm = ω R => 2 m/s = ω 0,2 m => ω = 10 rad/s
L = I ω = ½ M R2 ω = ½ 40 0,22 10 = 200 0,04 => L = 8 kg m2/s
4δ)
το κέντρο μάζας του κυλίνδρου έχει επιτάχυνση acm = 1 m/s2 το σημείο Α έχει 2αcm = 2 m/s2 και σε χρόνο t = 2 s διανύει χΑ = ½ 2 m/s2 (2 s)2 = 4 m
WF = F (AΓ) = 130 N 4 m = 520 J
K = ½ ½ M R2 ω2 + ½ Μ vcm2 = 1/4 M vcm2 + ½ Μ vcm2 = 3/4 M vcm2 = 3/4 40 22 = 120 J
U = Mg h = 40 10 1 = 400 J 400 J + 120 J = 520 J
τροποποίηση
ΘΕΜΑ Δ
Στην επιφάνεια ενός ομογενούς κυλίνδρου μάζας Μ = 40 kg και ακτίνας R = 0,2 m, έχουμε τυλίξει λεπτό σχοινί αμελητέας μάζας, το ελεύθερο άκρο του οποίου έλκεται με σταθερή δύναμη F παράλληλη προς την επιφάνεια κεκλιμένου επιπέδου γωνίας κλίσεως 30°, όπως φαίνεται στο σχήμα.
Το σχοινί ξετυλίγεται χωρίς ολίσθηση, περιστρέφοντας ταυτόχρονα τον κύλινδρο. Ο κύλινδρος κυλίεται πάνω στην επιφάνεια του κεκλιμένου επιπέδου χωρίς ολίσθηση.
α. Να υπολογισθεί το μέτρο της δύναμης F, ώστε ο κύλινδρος να ισορροπεί ακίνητος στο κεκλιμένο επίπεδο. Μονάδες 5
Αν αρχικά ο κύλινδρος είναι ακίνητος με το κέντρο μάζας του στη θέση Α και στο ελεύθερο άκρο του σχοινιού ασκηθεί σταθερή δύναμη F = 130N, όπως στο σχήμα, o κύλινδρος αποκτά σταθερή γωνιακή επιτάχυνση αγων = 5 rad/s2.
β. Να υπολογισθεί η στροφορμή στοιχειώδους μάζας Δm = 10-10 kg η οποία βρίσκεται σε απόσταση 2R από το κεκλιμένο, ως προς τον άξονα περιστροφής του κυλίνδρου όταν το κέντρο μάζας του κυλίνδρου περνάει από τη θέση Γ του σχήματος, η οποία βρίσκεται h = 1m ψηλότερα από τη θέση Α. Μονάδες 7
γ. Να υπολογισθεί το έργο της δύναμης F κατά τη μετακίνηση του κέντρου μάζας του κυλίνδρου από τη θέση Α στη θέση Γ Μονάδες 7
επιτάχυνση βαρύτητας g = 10m/s2.
4a) ο κύλινδρος ακίνητος άρα αcm = 0 και αγων = 0
F R - T R = 0 => F - T = 0 => F = T
F + T - Mg ημ30° = 0 => F + T - ½ Mg = 0 => 2F = ½ 40 10 => F = 100 N
4β)
R αγων = acm αγων = 5 rad/s2 acm = 1 m/s2
(AΓ) = h / ημ30° = 1m / 0,5 = 2 m = ½ acm t2 => t2 = 4 => t = 2 s vcm = acm t = 2 m/s
vcm = ω R => 2 m/s = ω 0,2 m => ω = 10 rad/s
L = Δm v R = Δm 2vcm R = 10-10 4 0,2 = 8 10-11 => L = 8 10-11 kg m2/s
4γ)
το κέντρο μάζας του κυλίνδρου έχει επιτάχυνση acm = 1 m/s2 το σημείο Α έχει 2αcm = 2 m/s2 και σε χρόνο t = 2 s διανύει χΑ = ½ 2 m/s2 (2 s)2 = 4 m
WF = F (AΓ) = 130 N 4 m = 520 J
επαναληπτικές ΣΕΠ 2007
ΘΕΜΑ 4ο
Ένα σώμα Σ μάζας m1 είναι δεμένο στο ένα άκρο οριζόντιου ελατηρίου σταθεράς Κ. Το άλλο άκρο του ελατηρίου είναι ακλόνητα στερεωμένο. Το σύστημα ελατήριο-μάζα εκτελεί απλή αρμονική ταλάντωση σε λείο οριζόντιο επίπεδο και τη χρονική στιγμή t=0 το σώμα Σ διέρχεται από τη θέση ισορροπίας του, κινούμενο κατά τη θετική φορά. Η εξίσωση της απομάκρυνσης της ταλάντωσης του σώματος Σ δίνεται από τη σχέση x = 0,1ημ10t (SI). Η ολική ενέργεια της ταλάντωσης είναι Ε = 6 J. Τη χρονική στιγμή t = π/10 s στο σώμα Σ σφηνώνεται βλήμα μάζας m2 = m1/2 κινούμενο με ταχύτητα υ2 κατά την αρνητική φορά. Το συσσωμάτωμα που προκύπτει μετά την κρούση εκτελεί νέα απλή αρμονική ταλάντωση πλάτους A' = 0,1√6 m.
α. Να υπολογίσετε τη σταθερά Κ του ελατηρίου (μονάδες 4) και τη μάζα m1 του σώματος Σ (μονάδες 4). Μονάδες 8
β. Να υπολογίσετε την ολική ενέργεια Ε ́ (μονάδες 4) και τη γωνιακή συχνότητα ω' της ταλάντωσης του
συσσωματώματος (μονάδες 4). Μονάδες 8
γ. Να υπολογίσετε την ταχύτητα υ2 του βλήματος πριν από την κρούση. Μονάδες 9
A = 0,1 m ω = 10 rad/s T = 2π/10 = π/5 s x = 0,1 ημ(10 π/10) = 0 το σώμα διέρχεται από τη Θ.Ι. του κινούμενο προς τα αριστερά με ταχύτητα υ1 = 1 συν(10 π/10) = - 1 m/s
x = 0,1 ημ10t υ = 1 συν10t α = - 10 ημ10t
Ε = ½ m1 v12 => 6 = ½ m1 12 => m1 = 12 kg
Ε = ½ k A2 => 6 = ½ k 0,12 => k = 1200 N/m
m1 v1 + m2 v2 = (m1 + m2) u => 12 (- 1) - 6 v2 = 18 u => - v2 - 2 = 3 u (1)
η Θ.Ι. του συσσωματώματος είναι η ίδια με τη Θ.Ι. του Σ1
Ε' = ½ k (A')2 = ½ 1200 0,12 6 = 36 J
k = (m1 + m2) (ω')2 => 1200 = 18 (ω')2 => (ω')2 = 200/3
Ε' = ½ (m1 + m2) u2 => 36 = ½ 18 u2 => u2 = 4 => u = - 2 m/s (2)
(1) , (2) => - v2 - 2 = 3 (- 2) => v2 = 4 m/s μέτρο ταχύτητας
επαναληπτικές ΣΕΠ 2006
ΘΕΜΑ 3ο
∆ύο σημαδούρες Α και Β απέχουν μεταξύ τους απόσταση ΑΒ = 13,5m και η ευθεία που διέρχεται από αυτές είναι κάθετη στην ακτογραμμή. Πλοίο που κινείται παράλληλα στην ακτογραμμή, μακριά από τις σημαδούρες δημιουργεί κύμα, με φορά διάδοσης από την Α προς την Β, το οποίο θεωρούμε εγκάρσιο αρμονικό. Το κύμα διαδίδεται προς την ακτή. Εξ αιτίας του κύματος η κάθε σημαδούρα διέρχεται από τη θέση ισορροπίας της 30 φορές το λεπτό. Ο χρόνος που απαιτείται, για να φθάσει ένα «όρος» του κύματος από τη σημαδούρα Α στη Β, είναι 9s. Η μέγιστη ταχύτητα ταλάντωσης κάθε σημαδούρας είναι π/5 m/s. Θεωρούμε ως αρχή μέτρησης των αποστάσεων τη σημαδούρα Α και ως αρχή μέτρησης των χρόνων τη στιγμή που η σημαδούρα Α βρίσκεται στη θέση ισορροπίας και κινείται προς τα θετικά.
α. Να υπολογιστεί το μήκος του κύματος. Μονάδες 6
β. Πόσο απέχει η σημαδούρα Α από την ακτή, αν αυτή βρίσκεται για 21η φορά στην ανώτερη θέση της ταλάντωσής της, όταν το κύμα φθάσει στην ακτή. Μονάδες 6
γ. Να γραφεί η εξίσωση ταλάντωσης της σημαδούρας Β, καθώς το κύμα διαδίδεται από τη σημαδούρα Α προς τη Β. Μονάδες 6
δ. Να βρεθεί το μέτρο της ταχύτητας ταλάντωσης της σημαδούρας Β κάποια χρονική στιγμή που η σημαδούρα
Α βρίσκεται στο ανώτατο σημείο της ταλάντωσής της. Μονάδες 7
(α) T = 4 s f = 1/4 Hz ω = 2π/4 = π/2 rad/s v = (AB)/t = 13,5m / 9s = 1,5 m/s λ = v / f = 1,5 / 0,25 = 6 m
vmax = ω Α => π/5 = π/2 Α => Α = 2/5 = 0,4 m
(β) Τ/4 + 20Τ = 81 s xA = 1,5 m/s 81 s = 81 + 40,5 = 121,5 m
(γ) y(x,t) = 0,4 ημ(π/2 t - 2πx/6) yΒ = 0,4 ημ(π/2 t - 2π 13,5 /6) = 0,4 ημ(π/2 t - 4,5π)
(δ) v(x,t) = 0,2π συν(π/2 t - 2πx/6) υΒ = 0,2π ημ(π/2 t - 4,5π) 13,5 = 6 + 6 + 1,5 = 2λ + λ/4

ΘΕΜΑ 4ο
Τροχαλία μάζας Μ = 6kg και ακτίνας R = 0,25m μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που
διέρχεται από το κέντρο της Ο.
Γύρω από την τροχαλία υπάρχει αβαρές και μη εκτατό νήμα. Στα άκρα του νήματος υπάρχουν σε κατακόρυφη θέση
τα σώματα Σ1 και Σ2 με μάζες m1 = 4kg και m2 = 1kg αντίστοιχα. Το σώμα Σ2 είναι κολλημένο με σώμα Σ3 μάζας m3 = 1kg, το οποίο συγκρατείται από κατακόρυφο ελατήριο σταθεράς k =100 Ν/m. Το σύστημα αρχικά ισορροπεί όπως φαίνεται στο σχήμα.  Κάποια χρονική στιγμή, την οποία θεωρούμε ως χρονική στιγμή μηδέν (t0 = 0), τα σώματα Σ2 και Σ3 αποκολλώνται και το Σ3 εκτελεί απλή αρμονική ταλάντωση κατά τη διεύθυνση της κατακορύφου.
Κάποια χρονική στιγμή, την οποία θεωρούμε ως χρονική στιγμή μηδέν (t0 = 0), τα σώματα Σ2 και Σ3 αποκολλώνται και το Σ3 εκτελεί απλή αρμονική ταλάντωση κατά τη διεύθυνση της κατακορύφου.
α. Nα υπολογιστεί το πλάτος της ταλάντωσης του σώματος Σ3. Μονάδες 6
β. Να γραφεί η εξίσωση της απομάκρυνσης του σώματος Σ3 σε συνάρτηση με το χρόνο, θεωρώντας ως θετική φορά, τη φορά προς τα επάνω. Μονάδες 6
γ. Να υπολογιστεί η γωνιακή επιτάχυνση της τροχαλίας μετά την αποκόλληση των σωμάτων Σ2 και Σ3. Μονάδες 6
δ. Να υπολογιστεί ο ρυθμός μεταβολής της κινητικής ενέργειας της τροχαλίας τη χρονική στιγμή t = 0,1 s. Μονάδες 7
∆ίνονται η ροπή αδράνειας της τροχαλίας ως προς άξονα που διέρχεται από το κέντρο μάζας της Ι = 1/2 MR2, η τριβή ανάμεσα στην τροχαλία και στο νήμα είναι αρκετά μεγάλη, ώστε να μην παρατηρείται ολίσθηση και g = 10 m/s2.
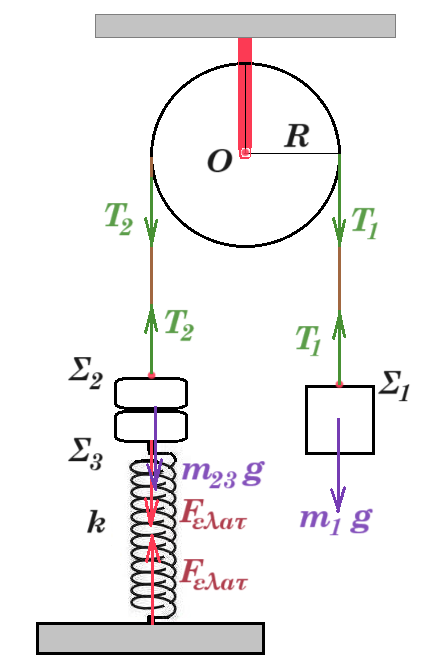
(α) ισορροπία Σ1 : Τ1 = m1 g = 40 N Στ(Ο) = 0 => T1 R = T2 R => T1 = T2 = 40 N
ισορροπία Σ2,3 : Τ2 = m2,3 g + Fελατ => Τ2 = m2,3 g + k Δl2,3 => 40 = 20 + 100 Δl => Δl2,3 = 0,2 m επιμήκυνση ελατηρίου
ισορροπία Σ3 : m3 g = k Δl3 => 10 = 100 Δl3 => Δl3 = 0,1 m συσπείρωση ελατηρίου
το πλάτος ταλάντωσης του Σ3 θα είναι : Α = Δl2,3 + Δl3 = 0,2 m + 0,1 m = 0,3 m = Α
(β) κυκλική συχνότητα ταλάντωσης Σ3 : ω2 = k / m3 = 100 / 1 => ω = 10 rad/s
x(t) = 0,3 ημ(10t + π/2) v(t) = 3 συν(10t + π/2) a(t) = - 30 ημ(10t + π/2)
(γ) η τροχαλία στρέφεται με γωνιακή επιτάχυνση αγων :
Στ(Ο) = Ι(Ο) αγων => T1 R - T2 R = ½ Μ R2 αγων => T1 - T2 = ½ Μ R αγων (1)
το Σ1 κατέρχεται : m1 g - Τ1 = m1 α = m1 αγων R (2)
το Σ2 ανέρχεται : Τ2 - m2 g = m2 α = m2 αγων R (3)
(1) + (2) + () => m1 g - m2 g = ½ Μ R αγων + m1 αγων R + m2 αγων R =>
=> 40 - 10 = ½ 6 1/4 αγων + 4 αγων 1/4 + 1 αγων 1/4 => 30 = 2 αγων => αγων = 15 rad/s2
(δ) K = ½ Ι ω2
dK/dt = I ω dω/dt = ½ Μ R2 ω αγων = ½ Μ R2 αγων2 t = ½ 6 1/16 152 0,1 = 675/160 J/s




















 Μια άλλη σφαίρα, όμοια με την προηγούμενη, εκτοξεύεται από το κατώτατο σημείο Δ του ημισφαιρίου με ταχύτητα υ = 6m/s και κυλίεται χωρίς ολίσθηση στο εσωτερικό του με κατεύθυνση το άκρο Ε.
Μια άλλη σφαίρα, όμοια με την προηγούμενη, εκτοξεύεται από το κατώτατο σημείο Δ του ημισφαιρίου με ταχύτητα υ = 6m/s και κυλίεται χωρίς ολίσθηση στο εσωτερικό του με κατεύθυνση το άκρο Ε.