eef διαγώνισμα προσομοίωσης

ΘΕΜΑ Δ

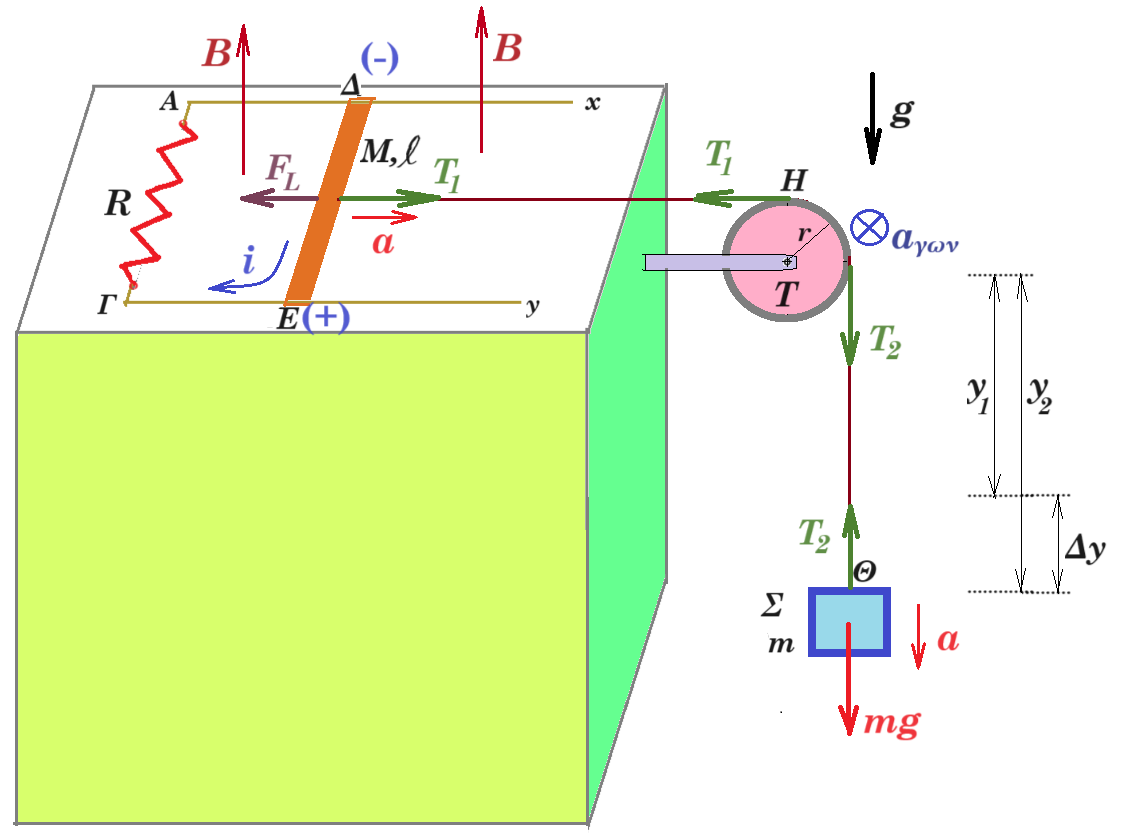
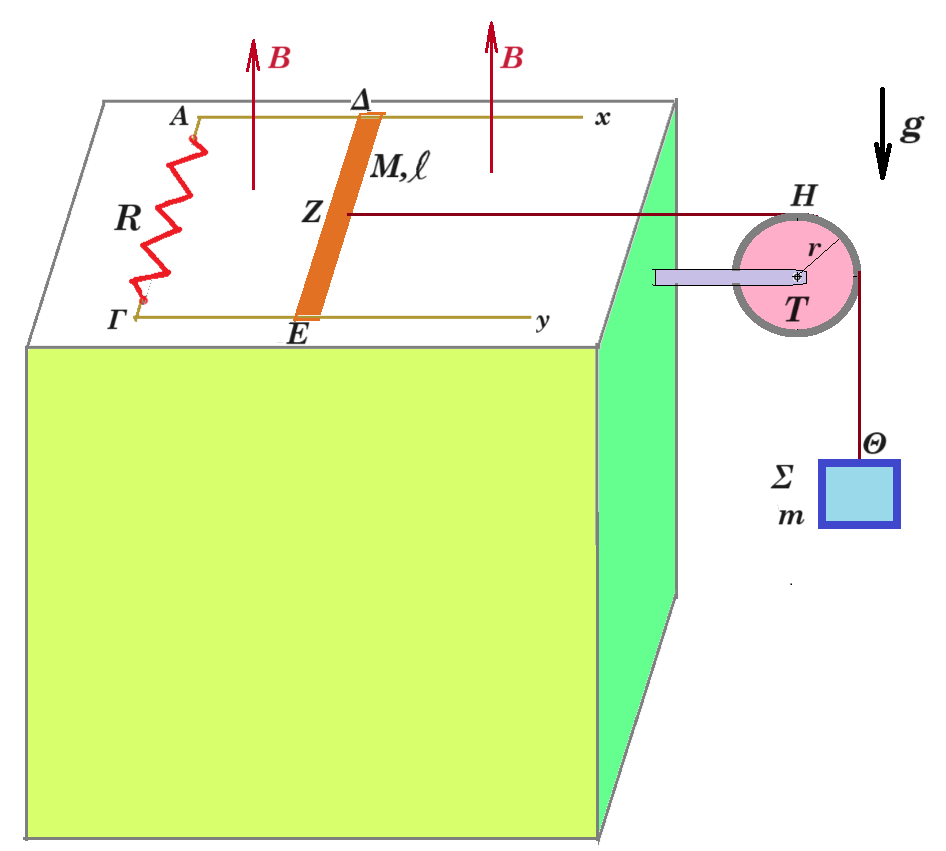
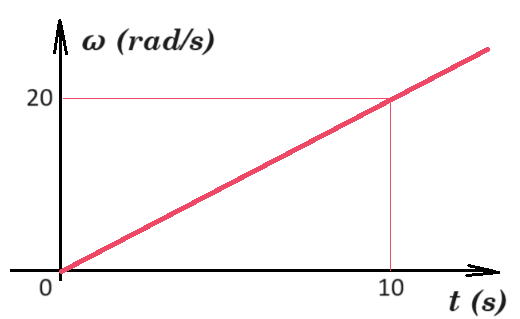
Οι αγωγοί Αx και Γy είναι παράλληλοι, απέχουν απόσταση 𝓵 = 𝟎,𝟓𝐦, ορίζουν το οριζόντιο επίπεδο και έχουν αμελητέα αντίσταση. Στα άκρα τους Α και Γ συνδέεται αντιστάτης, αντίστασης 𝐑 = 𝟎,𝟓𝛀. Το κατακόρυφο μαγνητικό πεδίο του σχήματος έχει μέτρο 𝚩 = 𝟐𝚻. Ο αγωγός ΔΕ έχει μάζα 𝚳 = 𝟏𝐤𝐠, μήκος 𝓵 και μπορεί να κινείται, χωρίς τριβές, μένοντας διαρκώς κάθετος και σε ηλεκτρική επαφή με τους αγωγούς Αx και Γy, εξαιτίας αβαρούς, μη εκτατού νήματος, του οποίου το ένα άκρο δένεται στο μέσο Ζ του αγωγού ΔΕ και το άλλο σε σημειακό αντικείμενο Θ, μάζας 𝐦 = 𝟏𝐤𝐠, αφού περάσει από το αυλάκι ακίνητης τροχαλίας Τ. Η τροχαλία Τ έχει ακτίνα 𝐫 = 𝟏𝟎𝐜𝐦. Τη χρονική στιγμή 𝐭_𝟎= 𝟎 ειδικός μηχανισμός θέτει την τροχαλία Τ σε δεξιόστροφη στροφική κίνηση. Την ίδια χρονική στιγμή αρχίζει να κινείται και ο αγωγός ΔΕ. Το μέτρο της γωνιακής ταχύτητας 𝛚 ⃗⃗⃗ της τροχαλίας Τ μεταβάλλεται με το χρόνο, όπως στο διάγραμμα.

Δίνεται το μέτρο της γήινης βαρυτικής επιτάχυνσης 𝐠 = 𝟏𝟎 𝐦/𝐬^𝟐. Το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλίας Τ.
Να υπολογίσετε:
Δ1. το μέτρο της γωνιακής επιτάχυνσης της τροχαλίας Τ.
Δ2. την ένταση και τη φορά του ρεύματος που διαρρέει τον αντιστάτη τη χρονική στιγμή 𝐭_𝟏= 𝟓𝐬.
Δ3. το μέτρο της τάσης 𝚻_𝟏του νήματος ΖΗ και το μέτρο της τάσης 𝚻_𝟐του νήματος ΗΘ.
Δ4. το ρυθμό ελάττωσης της βαρυτικής δυναμικής ενέργειας του σώματος Σ τη χρονική στιγμή 𝐭_𝟏= 𝟓𝐬 και τον αριθμό των περιστροφών της τροχαλίας εκείνη τη στιγμή.

Β1. Το οριζόντιο ομογενές μαγνητικό πεδίο 𝚩 ⃗⃗ της εικόνας εκτείνεται σε ζώνη πλάτους 𝓵 και άπειρου μήκους και βάθους.
Κατακόρυφη μεταλλική ράβδος, μήκους 𝐋 > 𝓵 κινείται με σταθερή ταχύτητα 𝛖, που είναι κάθετη τόσο στη ράβδο, όσο και στο μαγνητικό πεδίο. Η ράβδος έχει αντίσταση ανά μονάδα μήκους 𝐫∗. Τα άκρα της ράβδου συνδέονται αγώγιμα με αντιστάτη, αντίστασης 𝐑. Οι αγωγοί σύνδεσης έχουν αμελητέα αντίσταση.
Να χαρακτηρίσετε την πρόταση που ακολουθεί σωστή (Σ) ή λανθασμένη (Λ), αιτιολογώντας κατάλληλα τον χαρακτηρισμό σας.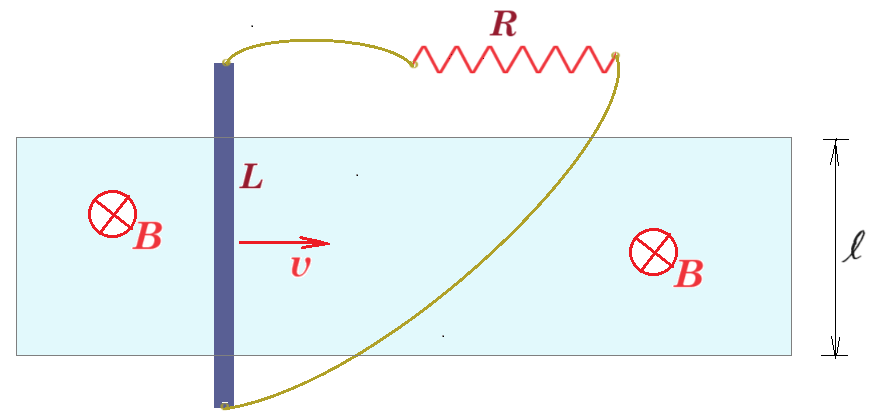

Η ηλεκτρεγερτική δύναμη (ΗΕΔ) που επάγεται στα άκρα της ράβδου είναι 𝓔𝛆𝛑 = 𝚩𝛖𝐋 και η ένταση του ρεύματος που διαρρέει τον αντιστάτη είναι 𝚰𝛆𝛑 = 𝚩𝛖𝓵/(𝐑+𝐫∗𝓵).

Β1. Το οριζόντιο ομογενές μαγνητικό πεδίο 𝚩 ⃗⃗ της εικόνας εκτείνεται σε ζώνη πλάτους 𝓵 και άπειρου μήκους και βάθους.
Κατακόρυφη μεταλλική ράβδος, μήκους 𝐋 > 𝓵 κινείται με σταθερή ταχύτητα 𝛖 ⃗ , που είναι κάθετη τόσο στη ράβδο, όσο και στο μαγνητικό πεδίο. Η ράβδος έχει αντίσταση ανά μονάδα μήκους 𝐫∗. Τα άκρα της ράβδου συνδέονται αγώγιμα με αντιστάτη, αντίστασης 𝐑. Οι αγωγοί σύνδεσης έχουν αμελητέα αντίσταση.
Να χαρακτηρίσετε την πρόταση που ακολουθεί σωστή (Σ) ή λανθασμένη (Λ), αιτιολογώντας κατάλληλα τον χαρακτηρισμό σας.

Η ηλεκτρεγερτική δύναμη (ΗΕΔ) που επάγεται στα άκρα της ράβδου είναι 𝓔𝛆𝛑 = 𝚩𝛖𝐋 και η ένταση του ρεύματος που
διαρρέει τον αντιστάτη είναι 𝚰𝛆𝛑 = 𝚩𝛖𝓵/(𝐑+𝐫∗𝓵).

Ε_επαγ = ΔΦ/Δt = B ΔA/Δt συν0° = B l Δx/Δt = Β l v

νόμος του Ohm για κλειστό κύκλωμα : Ε_επαγ = i (R + R_ράβδου) = i (R + r*L) => i = Β l v / (R + r*L)

Γ2. Ένα ταλαντούμενο άτομο κατεβαίνει δύο (2) σκαλοπάτια στην κλίμακα ενεργειακών σταθμών. Το φωτόνιο μέγιστης ενέργειας που εκπέμπεται είναι μόλις ικανό να προκαλέσει εκπομπή ενός φωτοηλεκτρονίου, όταν προσπέσει σε κάθοδο
φωτοηλεκτρικού σωλήνα, που είναι κατασκευασμένη από άργυρο (𝛟 = 𝟒,𝟑𝐞𝐕). Να υπολογίσετε το κβάντο ενέργειας αυτού του ταλαντωτή.
Γ3. Ένα φωτόνιο με μήκος κύματος στο κενό 𝛌_𝟎𝟏= 𝟐,𝟒𝟐∙𝟏𝟎^-𝟏𝟐𝐦, σκεδάζεται σε αρχικά ακίνητο ηλεκτρόνιο. Το σκεδαζόμενο φωτόνιο έχει μήκος κύματος στο κενό 𝛌_𝟎𝟐= 𝟒,𝟖𝟒∙𝟏𝟎^-𝟏𝟐𝐦.
Γ3α. Πόση είναι η ενέργεια του ανακρουόμενου ηλεκτρονίου;
Γ3β. Πόσο είναι το μέγιστο μήκος κύματος που πρέπει να έχει ένα φωτόνιο, το οποίο αν απορροφηθεί από κάθοδο φωτοηλεκτρικού σωλήνα, προκαλεί εκπομπή φωτοηλεκτρονίου με ενέργεια ίση με αυτή του ερωτήματος

2hf = 4,3eV => hf = 2,15eV

hc/λ₀₁ - hc/λ₀₂ = Κ_ε = 1242 / 2,42 eV - 1242 / 4,84 eV = 1242/4,84 eV = 256,6 eV
256,6 eV = hc/λ => λ = 1242 eV∙nm / 256,6 eV = 4,84 nm

ΘΕΜΑ Δ

Δίνεται το μέτρο της γήινης βαρυτικής επιτάχυνσης 𝐠 = 𝟏𝟎 𝐦/𝐬^𝟐. Το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλίας Τ.
Να υπολογίσετε:
Δ1. το μέτρο της γωνιακής επιτάχυνσης της τροχαλίας Τ.
Δ2. την ένταση και τη φορά του ρεύματος που διαρρέει τον αντιστάτη τη χρονική στιγμή 𝐭_𝟏= 𝟓𝐬.
Δ3. το μέτρο της τάσης 𝚻_𝟏του νήματος ΖΗ.
Δ4. το μέτρο της τάσης 𝚻_𝟐του νήματος ΗΘ.
Δ5. το ρυθμό ελάττωσης της βαρυτικής δυναμικής ενέργειας του σώματος Σ τη χρονική στιγμή 𝐭_𝟏= 𝟓𝐬 και τον αριθμό των περιστροφών της τροχαλίας εκείνη τη στιγμή.

Δ1. α_γων = Δω / Δt = 10 rad/s / 5 s = 2 rad/s² το σώμα κατέρχεται με επιτάχυνση α = α_γων r = 2 rad/s² 0,1 m = 0,2 m/s²

Δ2. Δ (-) Ε (+) Β l v = i R => 2 0,5 v = i 0,5 => 2v = i F_L = B l i = 2 0,5 2v = 2v

τη στιγμή t₁ = 5 s η γωνιακή ταχύτητα είναι ω = 10 rad/s ενώ η γραμμική ταχύτητα ενός σημείου στην περιφέρεια της τροχαλίας είναι v = ω r = 10 rad/s 0,1 m => v = 1 m/s οπότε η ένταση του επαγωγικού ρεύματος είναι i = 2v = 2 A οπότε F_L = 2 N

Δ3. T₁ - F_L = M a => T₁ - 2 = 1 0,2 => T₁ = 2,2 N

Δ4. mg -T₂ = m a => 10 - T₂ = 1 0,2 => T₂ = 9,8 N

Δ5. ΔU / Δt = - mg v = - 1 10 1 = - 10 J/s

ΔW = mg y₂ - mg y₁ = mg Δy ΔU = - ΔW ΔU / Δt - ΔW/Δt = - mg Δy/Δt = - mg v

θ = ½ α_γων t² = ½ 2 rad/s² 25 s² = 25 rad = N 2π r = N 2π 0,1 m => N = 125/π στροφές

τροχαλία : Στ_{(κέντρο της)} = Ι α_γων => ( Τ₂ - Τ₁ ) r = ½ Μ_τροχ r² α_γων => Τ₂ - Τ₁ = ½ Μ_τροχ r α_γων =>

=> 9,8 - 2,2 = ½ Μ_τροχ 0,1 2 => 7,6 = Μ_τροχ 0,1 => Μ_τροχ = 76 kg