Β2.  Ομογενής ράβδος ΚΛ, μάζας M και μήκους L, ισορροπεί οριζόντια, στηριζόμενη από υποστήριγμα (Υ) σε σημείο της Α (Σχήμα 1). Το αριστερό άκρο (Κ) της ράβδου είναι δεμένο με ιδανικό κατακόρυφο ελατήριο, το άλλο άκρο του οποίου είναι δεμένο στο έδαφος. Στο δεξιό άκρο (Λ) της ράβδου είναι τοποθετημένο σώμα (Σ) μάζας m.
Αν γνωρίζουμε ότι M = m/2 και (ΑΛ) = L/5, τότε το ελατήριο είναι:
α. επιμηκυμένο         β. συσπειρωμένο         γ. στο φυσικό του μήκος    Στ_(Α) = 0  =>  Mg (L/2 - L/5)  +  F_ελατ 4L/5  -  mg L/5  =  0  =>  Mg 3L/10  +  F_ελατ 4L/5  =  2Mg L/5  =>

  =>  F_ελατ 4L/5  =  Mg L/10  =>  F_ελατ =  M/2g = m/4g  ομόρροπη του βάρους της ράβδου  άρα το ελατήριο είναι επιμηκυμένο

Β3.   Δύο σημειακά φορτισμένα σωματίδια Σ1 και Σ2 να βρίσκονται μέσα σε ομογενή μαγνητικά πεδία με αντίρροπες εντάσεις μέτρων Β₁ και Β₂=Β₁, αντίστοιχα.
Δίνουμε στα σωματίδια αντίρροπες ταχύτητες μέτρων υ₁ και υ₂=2υ₁, οπότε αυτά εκτελούν ομαλή κυκλική κίνηση.
Αν για τις μάζες και τα φορτία των σωματιδίων γνωρίζουμε ότι: m₂= 3m₁ και |q₁|= |q₂|, με q₁>0 και q₂>0, τότε οι αλγεβρικές τιμές των στροφορμών των σωματιδίων συνδέονται με τη σχέση:
α. L₂= -36L₁          β. L₂= +36L₁            γ. L₂= -18L₁

   L = m v r = m v (m v) / (q B) = p²/ qB  = m² v²/ qB 

  L₁ = m₁² v₁² / q₁B₁      L₂ = m₂² v₂² / q₂B₂  =  9 m₁² 4 v₁² / q₁ (-B₁)  =  - 36 L₁ = L₂      (i)    

ΘΕΜΑ Γ
Σε μια χορδή, που τη θεωρούμε γραμμικό ελαστικό μέσο, διαδίδεται αρμονικό κύμα κατά τη θετική κατεύθυνση. Το σημείο Ο της χορδής, στη θέση x = 0, ξεκινάει να ταλαντώνεται τη χρονική στιγμή t₀ = 0 και έχει εξίσωση ταλάντωσης  y_Ο = 2ημ10πt.   Το κύμα διαδίδεται στη χορδή με ταχύτητα  υ = 10 m/s.
Γ1.  Να βρεθεί το μήκος κύματος και να γραφεί η εξίσωση του κύματος στο S.I.
Γ2.  Να γίνει το στιγμιότυπο του κύματος τη χρονική στιγμή t₁ = 0,5 sec.
Γ3.  Ένα σημείο Κ του ελαστικού μέσου βρίσκεται στη θέση x_K = +8 m. Να γίνει η γραφική παράσταση της απομάκρυνσης του σημείου Κ από τη θέση ισορροπίας του σε συνάρτηση με τον χρόνο, από τη χρονική στιγμή  t₀ = 0 έως τη χρονική στιγμή  t₂ = 1,2 sec.
Γ4.  Ένα δεύτερο κύμα που διαδίδεται στην ίδια χορδή προς την αρνητική κατεύθυνση, συμβάλει με το αρχικό κύμα με αποτέλεσμα να δημιουργηθεί στάσιμο κύμα. Να γραφεί η εξίσωση του δεύτερου κύματος στο S.I.  και η εξίσωση του στάσιμου κύματος στο S.I.

   ω = 10π rad/s     f = 5 Hz      T = 1/5 = 0,2 s      A = 2 m         λ = v / f = 10 m/s / 5 Hz = 2 m

    y = 2 ημ(10πt - 2πx/λ) = 2 ημ(10πt - 2πx/2) =>  y = 2 ημ(10πt - πx)  

  t₁ = 0,5 s = 0,2 + 0,2 + 0,1 = 2T + T/2       y = 2 ημ(10π 0,5 - πx)  = 2 ημ(5π - πx)  => y = 2 ημ(πx)  

     t₂ = 1,2 s = 6 ^. 0,2s = 6T             το κύμα θέλει χρόνο  t = 8m / 10m/s = 0,8s  για να φθάσει στο σημείο Κ από την πηγή Ο άρα

  y_K = 0    0 £ t £ 0,8s         &        y_K = 2 ημ(10πt - 8π)  = 2 ημ(10πt)     0,8s £ t £ 1,2s            

     y₁ = 2 ημ(10πt - πx)       y₂ = 2 ημ(10πt + πx)          y₁ + y₂ = 4 συν(πx) ημ(10πt)

ΘΕΜΑ Δ
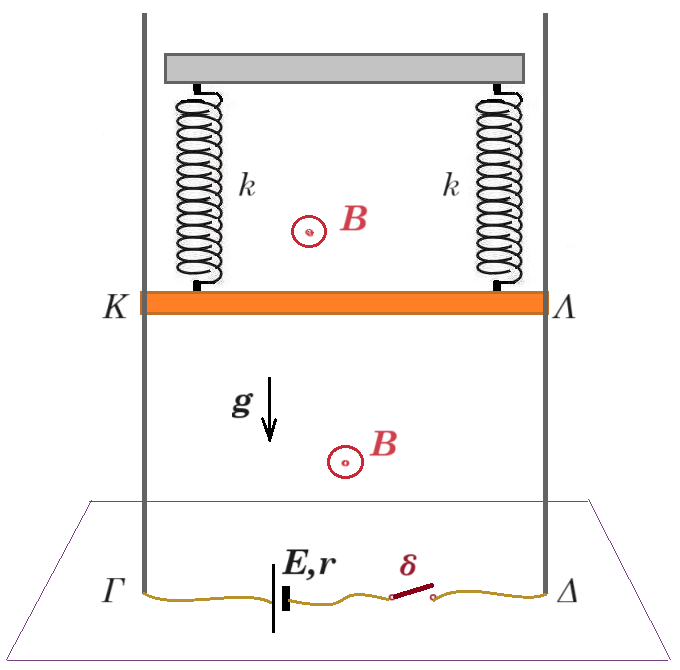
Η ράβδος ΚΛ  έχει μάζα m, μήκος  l =1m και αντίσταση R=4Ω και είναι αναρτημένη από δύο ιδανικά κατακόρυφα μονωτικά ελατήρια ίδιας σταθεράς k=100 N/m, τα άλλα άκρα των οποίων είναι ακλόνητα στερεωμένα στο ταβάνι. Η ράβδος είναι συνεχώς οριζόντια και σε επαφή με κατακόρυφα σύρματα, τα οποία δεν παρουσιάζουν ούτε αντίσταση, ούτε τριβή. Μεταξύ των σημείων Γ & Δ υπάρχει ηλεκτρική πηγή με στοιχεία Ε=50V και  r=1Ω. Ο διακόπτης δ είναι αρχικά κλειστός και το σύστημα ισορροπεί μέσα σε ομογενές οριζόντιο μαγνητικό πεδίο έντασης Β=2Τ. 
Δ1.  Αν η αρχική επιμήκυνση των ελατηρίων από το φυσικό μήκος είναι  Δl=0,2m να βρεθεί η μάζα m της ράβδου.
Στη συνέχεια ανοίγουμε τον διακόπτη δ και η ράβδος ξεκινάει να ταλαντώνεται αρμονικά με σταθερά επαναφοράς D=2k. Θετική φορά για την ταλάντωση να θεωρηθεί η προς τα κάτω.
Να βρεθούν:
Δ2.  Η εξίσωση θέσης x(t) της ταλάντωσης της ράβδου.
Δ3.  Ο λόγος των μέτρων της μέγιστης δύναμης επαναφοράς προς τη μέγιστη ολική δύναμη των ελατηρίων.
Δ4.  Η εξίσωση της επαγωγικής τάσης στα άκρα της ράβδου σε συνάρτηση με τον χρόνο. Στη συνέχεια να γίνει η γραφική παράσταση της τάσης με τον χρόνο σε βαθμονομημένους άξονες για το χρονικό διάστημα από 0 έως 2π/5 sec.

κλειστός διακόπτης       E = i (R + r)  =>  i = 50 V / 5 Ω = 10 Α 

   ισορροπία ράβδου ΚΛ :  mg + B l i = 2k Δl  =>  m  10  +  2  1  10  =  200  0,2  =>  m = 2 kg

ανοικτός διακόπτης   ισορροπία ράβδου :   mg  - 2k Δl'  = 0  =>  20 = 200  Δl'  =>  Δl' = 0,1 m  επιμήκυνση ελατηρίου          ω = ( 2k/m )^½ =  ( 200 / 2 )^½ = 10 rad/s    Τ = 2π/ω = π/5 rad/s

αρχικά τα ελατήρια είναι επιμηκυμένα κατά Δl = 0,2 m   άρα  το πλάτος της ταλάντωσης θα είναι :  Α = Δl - Δl' = 0,1 m   και η αρχική φάση  + π/2    τότε   x(t) = 0,1 ημ(10t + π/2)

  v(t) = 1 συν(10t + π/2)     α(t) = - 10 ημ(10t + π/2)

ΣF = ma  =>  mg + F_ελατ = ma  =>  F_ελατ(t) =  - 20  - 20 ημ(10t + π/2)     |F_ελατ,max| = 40 N

  F_ελατ(x) =  - 20  - 200 ^. x     - 0,1m  £  x  £  + 0,1m  

ΣF = ma  => ΣF(t) = - 20 ημ(10t + π/2)    |ΣF_max| = 20 N         |ΣF_max|/|F_ελατ,max| = 1/2 

Ε_επαγ = Β l v = 2  1  1 συν(10t + π/2)  = 2 συν(10t + π/2) => Ε_επαγ = - 2 ημ(10t)      0 £ t £  2π/5 s = 2T