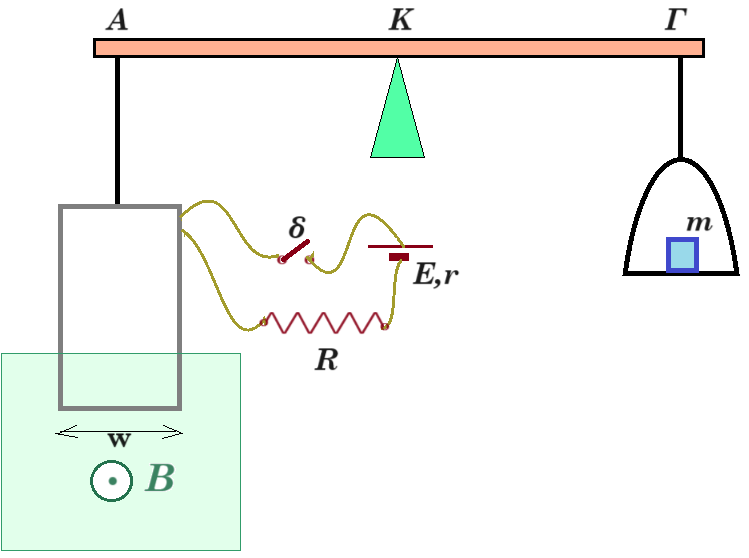
Β.1.  Το σχήμα δείχνει τη σχηματική αναπαράσταση μιας συσκευής που μπορεί να χρησιμοποιηθεί για τη μέτρηση μαγνητικών πεδίων. Ένα ορθογώνιο συρμάτινο πλαίσιο αμελητέας αντίστασης αποτελείται από N = 50 σπείρες και έχει πλάτος w = 5cm. Το πλαίσιο είναι αναρτημένο στον ένα βραχίονα ενός ζυγού στο σημείο Α και αιωρείται μεταξύ των πόλων ενός μαγνήτη. Ο βραχίονας έχει αμελητέα μάζα. Στο σημείο Γ είναι αναρτημένος ο δίσκος του ζυγού. Το μαγνητικό πεδίο είναι ομογενές και κάθετο στο κατακόρυφο επίπεδο του πλαισίου. Η ηλεκτρική πηγή είναι ιδανική με ΗΕΔ Ɛ = 3V και ο αντιστάτης έχει ωμική αντίσταση R = 10Ω. Όταν το ρεύμα στο πλαίσιο είναι μηδέν, το σύστημα ισορροπεί και το στήριγμα στο σημείο Κ βρίσκεται στο μέσο της απόστασης ΑΓ. Όταν ο διακόπτης Δ είναι κλειστός και το πλαίσιο διαρρέεται από ρεύμα, πρέπει να προστεθεί μια μάζα m = 20g στον δίσκο στη δεξιά πλευρά για ναισορροπήσει και πάλι το σύστημα χωρίς να μετακινηθεί ο βραχίονας. Αν δίνεται ότι η επιτάχυνση της βαρύτητας έχει μέτρο g =10 m/s², τότε το μέτρο της έντασης του μαγνητικού πεδίου Β είναι:

  α)  Β = 4/15 Τ         β)  Β = 2/5 Τ           γ)  Β = 1/4 Τ 

  i = E / R = 3V / 10Ω = 0,3 Α  

  mg = Bw Νi =>  0,02kg  10m/s²  =  Β  0,05m  50σπείρες 0,3A  =>  0,2 = Β 0,75  =>  1/5 = Β 3/4  =>  Β = 4/15 Τ

Β.2  Ένα ομογενές μαγνητικό πεδίο έντασης Β έχει κατεύθυνση κατά μήκος του θετικού ημιάξονα Οx. Ένα ποζιτρόνιο e+ (σωματίδιο που έχει ίδια μάζα με το ηλεκτρόνιο και αντίθετο φορτίο) κινείται με ταχύτητα u  και εισέρχεται στο πεδίο κατά μήκος μιας κατεύθυνσης που σχηματίζει γωνία θ με τον ημιάξονα Οx. Για την γωνία θ ισχύει ότι εφθ=2. Η κίνηση του σωματιδίου είναι ελικοειδής.
Αν η ακτίνα της κυκλικής τροχιάς είναι r = 2cm, τότε το βήμα β της έλικας είναι :  α)  π cm     β)  2π cm     γ)  π/2 cm

r = mu ημθ / qB  => ημθ = rqB / m∙u     T = 2πm / qB    

   β = u συνθ Τ = u συνθ 2πm / qB  =>  συνθ = β qB / 2π∙m∙u 

  εφθ =  2π r / β  =>  2 = 2π 2cm / β  =>  β = 2π cm    

ΘΕΜΑ Γ
Κατά μήκος ενός γραμμικού ελαστικού μέσου διαδίδεται προς τη θετική κατεύθυνση, με ταχύτητα υ=2m/s, ένα αρμονικό κύμα, πλάτους Α=0,2m. Τη χρονική στιγμή t=0, το κύμα φτάνει στο σημείο Ο, στην αρχή (x=0), ενός προσανατολισμένου άξονα x ́x.  Το σημείο Ο αρχίζει να ταλαντώνεται, κινούμενο προς τη θετική φορά του άξονα y ́y, και φθάνει στη θέση μέγιστης απομάκρυνσης, για πρώτη φορά μετά από χρονικό διάστημα 0,5s .
Γ.1. Θεωρήστε ένα τυχαίο σημείο του ελαστικού μέσου με θέση ισορροπίας x>0. Να δείξετε πως η εξίσωση του αρμονικού κύματος δίνεται από τη σχέση:  y = A ημ2π((t/T - x/λ)  και να κάνετε αντικατάσταση των τιμών πλάτους, περιόδου, μήκους κύματος. (Μονάδες 8)
Γ.2. Να γράψετε την εξίσωση που περιγράφει την απομάκρυνση  y_Σ = f(t) του σημείου Σ του μέσου στη θέση x_Σ = 2m και να σχεδιάσετε την αντίστοιχη γραφική παράσταση μέχρι το σημείο Σ να ολοκληρώσει δύο ταλαντώσεις. (Μονάδες 8)

Γ.3. Να γράψετε την εξίσωση που περιγράφει το στιγμιότυπο του κύματος τη χρονική στιγμή t₁=4,5s και να σχεδιάσετε το στιγμιότυπο y = f(x)  για x  0 και τη γραφική παράσταση της φάσης του κύματος  y = f (x) για x  0 , την ίδια χρονική στιγμή. (Μονάδες 9)

Γ.1.   T = 4 ∙ 0,5 s = 2 s            λ = v T = 2 m/s  2 s = 4 m  

το κύμα θέλει χρόνο x/v για να φθάσει από την πηγή σε κάποιο σημείο   y = A ημω(t - x/v) = A ημ [ 2π/Τ (t - x/v) ]  =  A ημ2π(t/T - x/υΤ)  =>  y = A ημ2π(t/T - x/λ) = 0,2 ημ2π(t/2 - x/4)  => y = 0,2 ημπ(t - x/2) 

Γ.2.  το κύμα φθάνει στο σημείο Σ  σε χρόνο  2m / 2m/s = 1 s   

y_Σ = 0,2 ημπ(t - 2/2) = 0,2 ημ(πt - π) = - 0,2 ημ(πt)  =>   y_Σ(t) =  - 0,2 ημ(πt)      1s £  t £ 5s = 1s + 2Τ

Γ.3.   t=4,5s :  y = 0,2 ημπ(4,5 - x/2) = 0,2 ημ(4π+π/2 - xπ/2) = 0,2 ημ(π/2 - xπ/2) = 0,2 συν(xπ/2) x  0

   φ = π(4,5 - x/2) , x  0

ΘΕΜΑ Δ
Σε ένα πυρηνικό πείραμα, ένας πυρήνας Ηλίου (Ηe) μάζας m = 6,4 ∙ 10^-27 Kg και ηλεκτρικού φορτίου q = 3,2 ∙ 10^-19 C, κινείται μέσα σε ομογενές μαγνητικό πεδίο έντασης μέτρου Β = 0,1Τ, κάθετα στις δυναμικές γραμμές του πεδίου και διαγράφει κυκλική τροχιά ακτίνας R₁ = 6cm. Κάποια στιγμή ο πυρήνας He διαπερνά ένα λεπτό φύλλο μολύβδου, οπότε χάνει ενέργεια. Αμέσως μετά συνεχίζει να κινείται μέσα στο ίδιο ομογενές μαγνητικό πεδίο αλλά σε κυκλική τροχιά ακτίνας R₂ = 2cm.
Να υπολογίσετε:
Δ.1. την περίοδο της κυκλικής κίνησης του πυρήνα He πριν περάσει το φύλλο του μολύβδου και αφού το διαπεράσει. Τι παρατηρείτε;       Μονάδες 6
Δ.2. το μήκος κύματος de Broglie που αντιστοιχεί στον πυρήνα He πριν διαπεράσει το φύλλο μολύβδου.    Μονάδες 7
Δ.3. το ποσοστό επί τοις εκατό της μεταβολής του μήκους κύματος de Broglie που αντιστοιχεί στον πυρήνα He αφού διαπεράσει το φύλλο μολύβδου.      Μονάδες 6
Δ.4. την απώλεια ενέργειας του πυρήνα He κατά το πέρασμά του μέσα από το φύλλο του μολύβδου.     Μονάδες 6

Να θεωρήσετε ότι η σταθερά του Planck έχει τιμή h = 6,6 ∙ 10^-34 J∙s.

R₁ = mv₁ / qB  =>  v₁ =  0,06  3,2 ∙ 10^-19  0,1 / 6,4 ∙ 10^-27  = 3 ∙ 10⁵ m/s  

R₂ = mv₂ / qB  =>  v₂ =  0,02  3,2 ∙ 10^-19  0,1 / 6,4 ∙ 10^-27  = 10⁵ m/s  

T₁ = 2πm / qB =  2π  6,4 ∙ 10^-27 / 3,2 ∙ 10^-19  0,1  = 4π ∙ 10^-7 sec  = T₂  δεν μεταβάλλεται   

λ₁ = h / p = h / mv₁ = 6,6 ∙ 10^-34 /  6,4 ∙ 10^-27 3 ∙ 10⁵ = 1/3 ∙ 10^-12 m

λ₂ = h / p = h / mv₂ = 6,6 ∙ 10^-34 /  6,4 ∙ 10^-27∙ 10⁵ =  10^-12 m     

 Δλ = λ₂ - λ₁ = 2/3 ∙ 10^-12 m        Δλ / λ₁ =  2/3 ∙ 10^-12 /  1/3 ∙ 10^-12 = 2

ΔΚ = ½ m v₂²  -  ½ m v₁²  = ½ m (v₂²  - v₁²)  =  ½  6,4 ∙ 10^-27  ( 10¹⁰ - 9 ∙ 10¹⁰)  =  - 25,6 ∙ 10^-17 J