ΘΕΜΑ Α
Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά την ημιτελή πρόταση.
Α.1. Ας θεωρήσουμε το πρότυπο του Bohr για το άτομο του υδρογόνου. Στη θεμελιώδη κατάσταση, το άτομο έχει ενέργεια 𝚬𝟏, ενώ το ηλεκτρόνιό του περιφέρεται σε κυκλική τροχιά, ακτίνας 𝐫𝟏, με κέντρο τον πυρήνα του. Στο κέντρο αυτής της κυκλικής τροχιάς, σύμφωνα με τον Bohr, το γινόμενο |𝚿𝟐|𝐝𝐕, όπου 𝚿 η κυματοσυνάρτηση του ηλεκτρονίου και 𝐝𝐕 ένας στοιχειώδης όγκος γύρω από το σημείο αυτό, θα είχε τιμή:
α) |𝚿𝟐|𝐝𝐕 = 𝟎, β) |𝚿𝟐|𝐝𝐕 = 𝟏, γ) 𝟎 < |𝚿𝟐|𝐝𝐕 < 𝟏, δ) τίποτα από αυτά.
Επιλέξτε την σωστή απάντηση. μονάδες 5
Α.2. Στο φάσμα της ηλεκτρομαγνητικής ακτινοβολίας
α) οι ακτίνες Χ έχουν μεγαλύτερο μήκος κύματος από τα ραδιοκύματα και μεγαλύτερη συχνότητα από το υπέρυθρο
β) το ερυθρό φως έχει μεγαλύτερο μήκος κύματος από το πράσινο φως και μεγαλύτερη συχνότητα από τις ακτίνες Χ
γ) τα μικροκύματα έχουν μικρότερο μήκος κύματος από τα ραδιοκύματα και μικρότερη συχνότητα από το υπεριώδες
δ) το πορτοκαλί φως έχει μικρότερο μήκος κύματος από τις ακτίνες Χ και μεγαλύτερη συχνότητα από το υπεριώδες.
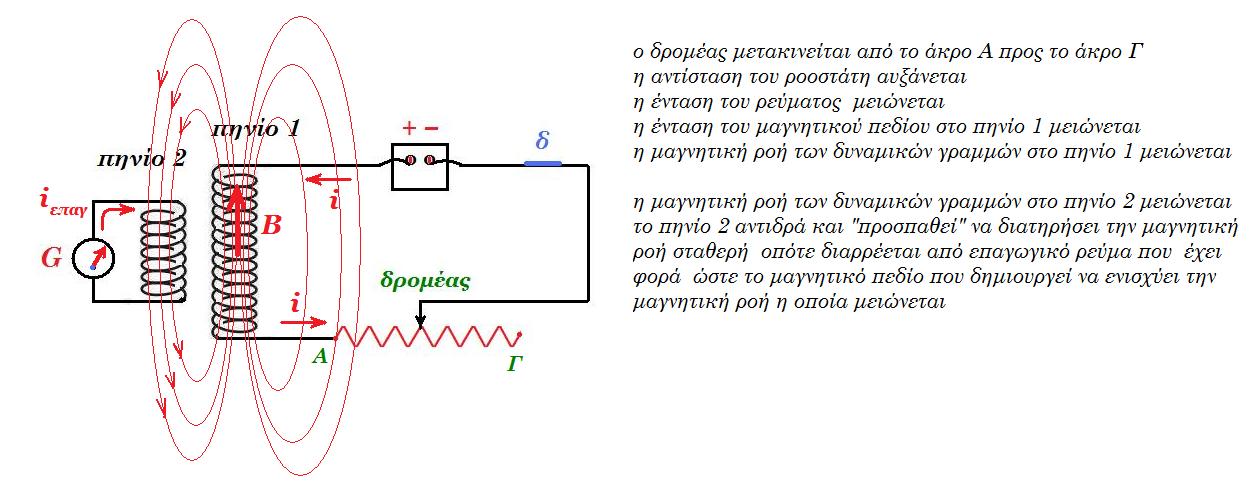
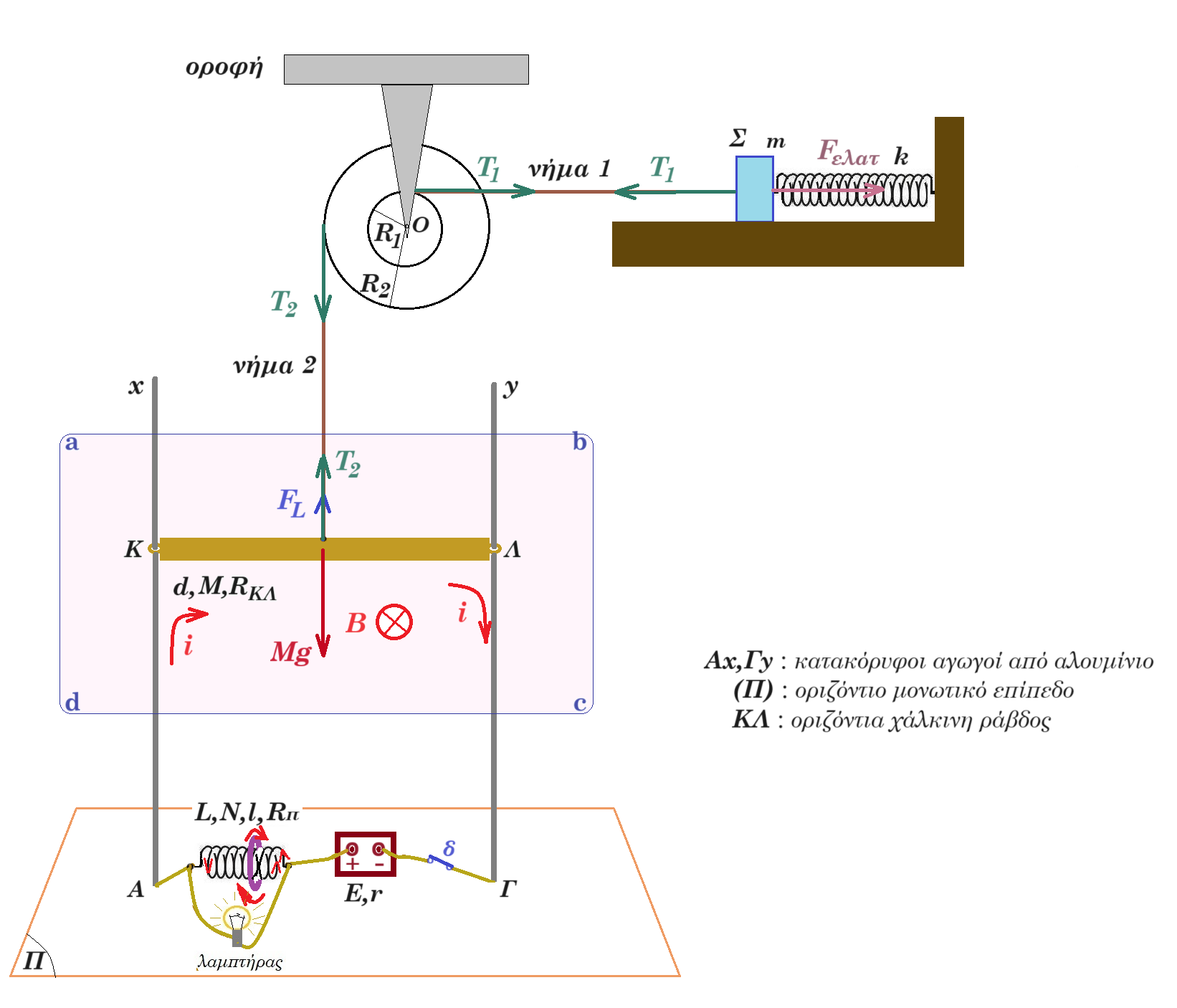
Α.4.α) Στο σχήμα ο δρομέας της μεταβλητής αντίστασης μετακινείται από το άκρο Α προς στο άκρο Γ.
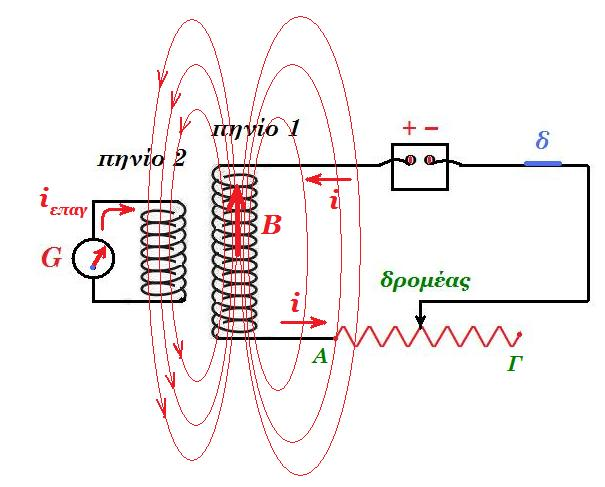α) Η ροή των δυναμικών γραμμών του μαγνητικού πεδίου στο πηνίο 1 αυξάνεται.
β) Το πηνίο 2 διαρρέεται από επαγωγικό ρεύμα όπως έχει σημειωθεί στο σχήμα.
γ) Η ένταση του μαγνητικού πεδίου που δημιουργείται στο πηνίο 1 έχει αντίθετη κατεύθυνση.
δ) Τίποτα από τα παραπάνω.
Επιλέξτε την σωστή απάντηση. μονάδες 2
Α.4.β) Στο κύκλωμα του σχήματος μια ηλεκτρική πηγή συνεχούς ρεύματος συνδέεται με μεταβλητή αντίσταση (ροοστάτης) και δύο κλάδους παράλληλους. Ο ένας κλάδος περιλαμβάνει λαμπτήρα με ωμική αντίσταση RΛ και ο άλλος πηνίο με ωμική αντίσταση Rπ ( RΛ < Rπ ). Ο διακόπτης δ είναι κλειστός. Τοποθετούμε τον δρομέα σε ορισμένη θέση έτσι ώστε ο λαμπτήρας να φωτοβολεί ελάχιστα και ανοίγουμε τον διακόπτη. 
α) Ο λαμπτήρας σβήνει αμέσως.
β) Ο λαμπτήρας φωτοβολεί αμυδρά για κάποιο χρονικό διάστημα και μετά σβήνει.
γ) Ο λαπτήρας αρχικά φωτοβολεί πιο έντονα και σβήνει μετά από κάποιο χρονικό διάστημα.
δ) Τίποτα από τα παραπάνω.
Επιλέξτε την σωστή απάντηση. μονάδες 3
Α.5. μονάδες 5
Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα την λέξη Σωστό, για την σωστή πρόταση, και την λέξη Λάθος, για την λανθασμένη.
α. Μεταλλική σφαίρα αμελητέας ακτίνας φέρει ηλεκτρικό φορτίο - 17∙10-19 C.
β. Ένα (1) Henry ισούται με 1 J/A2
γ. Σε χαμηλές θερμοκρασίες το μέλαν σώμα εκπέμπει στο υπέρυθρο.
δ. Hλεκτρόνιο περιστρέφεται γύρω από συνεχώς ακίνητο πρωτόνιο με σταθερή συχνότητα περιστροφής f σε ακτίνα r. Το διάνυσμα της στροφορμής L του ηλεκτρονίου και το διάνυσμα της έντασης Β του μαγνητικού πεδίου που δημιουργεί, είναι ομόρροπα.
ε. Στα άκρα αντίστασης 5 Ω εφαρμόζεται εναλλασσόμενη τάση. Η ισχύς που καταναλώνεται στην αντίσταση φαίνεται στο διάγραμμα P(t). H εξίσωση του ρεύματος που διαρρέει την αντίσταση συναρτήσει του χρόνου είναι : i(t) = 2∙ημ(10πt).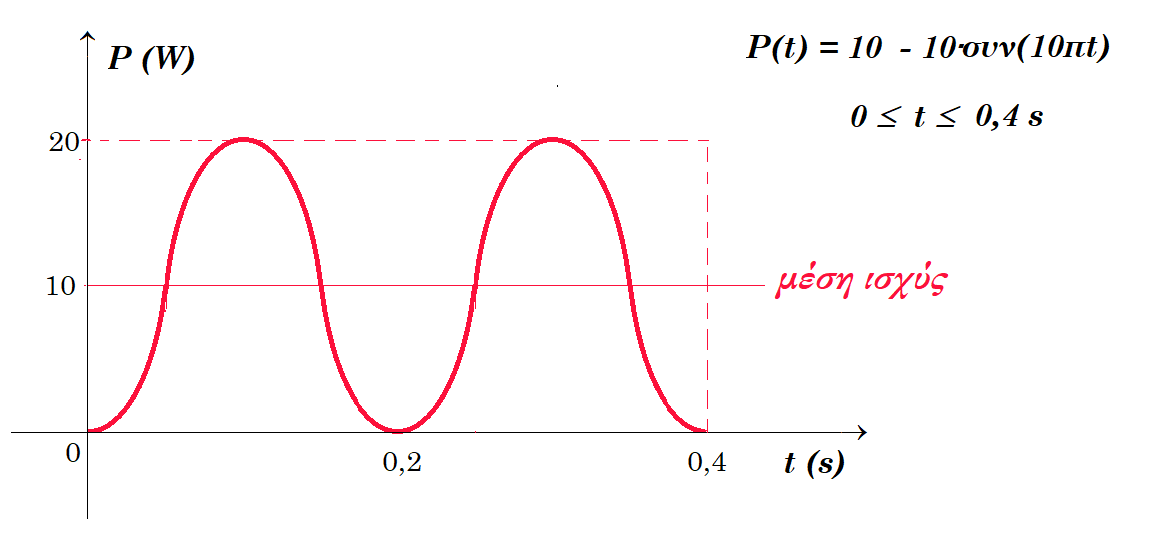
ΘΕΜΑ Γ
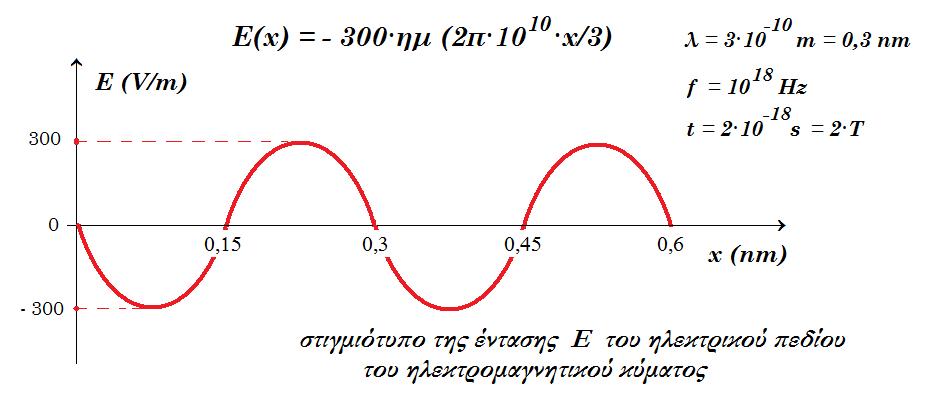
H εξίσωση που περιγράφει την ένταση του ηλεκτρικού πεδίου σε ένα ηλεκτρομαγνητικό κύμα το οποίο διαδίδεται στο κενό ή στην ατμόσφαιρα της Γης είναι : Ε(x,t) = 300∙ημ(2π∙1018t - 2π∙x/λ) (SI). Θεωρούμε Ε(x=0,t=0) = 0.
Γ1. Σε ποια περιοχή του Η/Μ φάσματος ανήκει το κύμα; μονάδες 3
Σχεδιάστε την ένταση του μαγνητικού πεδίου του κύματος συναρτήσει του x (x>0) για t=2∙10-18s. μονάδες 5
Γ2. Ένα φωτόνιο της ηλεκτρομαγνητικής ακτινοβολίας συχνότητας f = 1020 Hz σκεδάζεται από ένα ακίνητο ηλεκτρόνιο. Το σκεδαζόμενο φωτόνιο κινείται κάθετα προς τη διεύθυνση του προσπίπτοντος φωτονίου. Στο χώρο υπάρχει ομογενές μαγνητικό πεδίο εντάσεως Β=0,01Τ. Yπολογίστε την εφαπτομένη της γωνίας που σχηματίζει η ταχύτητα του ηλεκτρονίου αμέσως μετά την σκέδαση, με τη διεύθυνση της κίνησης του αρχικού φωτονίου και μελετήστε την κίνηση του σκεδαζόμενου ηλεκτρονίου μέσα στο μαγνητικό πεδίο εάν η ταχύτητά του αμέσως μετά την σκέδαση σχηματίζει με τις δυναμικές γραμμές του πεδίου γωνία 45°. μονάδες 6+3
h = 6,63∙10-34 J.s h / mc = 2,4 pm c = 3∙108 m/s 1 eV = 1,6∙10-19 J λ' - λ = h / mc (1 - συνφ)
Γ3. Στο σχήμα φαίνεται η διάταξη για την εξαγωγή ηλεκτρονίων από μια μεταλλική επιφάνεια όταν προσπέσει σ'αυτή ακτινοβολία Εφωτονίου = hf. Δεδομένα : E = 12 V r = 1 Ω RΚΛ = 10 Ω (ΚΛ) = 0,5 m
Φ ω τ ο η λ ε κ τ ρ ι κ ό
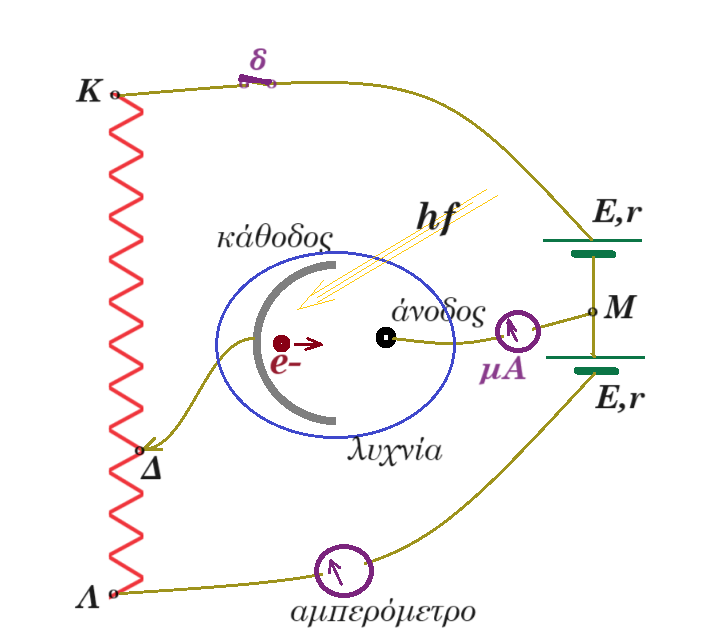
Μετακινώντας τον δρομέα Δ από το άκρο Κ έως το άκρο Λ της αντίστασης λαμβάνουμε τάση VMΔ θετική, αρνητική ή μηδενική. Έστω ότι ο δρομέας είναι στη θέση όπου (ΚΔ) = 0,3 m. Εάν στην κάθοδο προσπέσει ακτινοβολία συχνότητας : f=6∙1014Hz υπολογίστε την κινητική ενέργεια ενός ηλεκτρονίου που εξέρχεται από την επιφάνεια του μετάλλου, όταν φθάνει στην άνοδο. Έργο εξαγωγής μετάλλου φ =2,4 eV. μονάδες 8
Γ1. εξίσωση έντασης του ηλεκτρικού πεδίου Ε(x,t) = E0 ημ 2π(ft - x/λ) = 300· ημ 2π(1018 t - x/λ ) (S.I.)
f = 1018 Hz c = λ f => λ = c / f = 3·108m/s / 1018 Hz => λ = 3·10-10m = 0,3 nm < 400 nm (ιώδες) aκτίνες Χ
B0 = Ε0 / c => Β0 = 300 V/m / 3·108 m/s = 10-6 Τ
εξίσωση έντασης μαγνητικού πεδίου Β(x,t) = B0 ημ 2π( ft - x/λ ) = 10-6· ημ 2π(1018 t - 1010 x/3 ) (S.I.)
t=2·10-18s B(x) = 10-6 · ημ 2π(1018·2·10-18 - 1010 x/3 ) = 10-6 ·ημ (4π - 2π·1010·x/3) => B(x) = - 10-6 ·ημ (2π·1010·x/3)
t=2·10-18s Ε(x) = 300·ημ 2π(1018·2·10-18 - 1010 x/3 ) = 300·ημ (4π - 2π·1010·x/3) => Ε(x) = - 300·ημ (2π·1010·x/3)
Γ2. E = h f = 6,6 10-34 J.s 1020 Hz = 6,6 10-14 J ενέργεια προσπίπτοντος φωτονίου
λ = c / f = 3·108m/s / 1020 Hz => λ = 3·10-12m = 3 pm
φαινόμενο Compton : λ' - λ = h / mc ( 1 - συν90° ) =>
=> λ' - 3 10-12 m = 6,6 10-34 / ( 9 10-31 3 108 ) ( 1 - 0 ) = 0,24 10-11 m => λ' - 3 10-12 m = 2,4 10-12 m =>
=> λ' = 5,4 10-12 m = 5,4 pm
f ' = c / λ' = 3 108 / 5,4 10-12 = 0,55 1020 Hz συχνότητα σκεδαζομένου φωτονίου
ενέργεια σκεδαζομένου φωτονίου : E' = h f ' = 6,6 10-34 J.s 0,55 1020 Hz = 3,63 10-14 J = 2,27 .103 eV
διατήρηση ορμής : pe,x = E/c => pe συνθ = h / λ (1) pe,y = E'/c => pe ημθ = h / λ' (2)
(2) / (1) => εφθ = λ / λ' = 3 pm / 5,4 pm => εφθ = 5/9 = 0,55
Γ3.
Ισχύει η διατήρηση της ενέργειας : h.f + e.VMΔ = Ke + φ
όπου φ είναι το έργο εξαγωγής του μετάλλου δηλαδή η ενέργεια που πρέπει να προσλάβει το ηλεκτρόνιο του ατόμου της μεταλλικής επιφάνειας για να εξέλθει του ατόμου, το άτομο γίνεται ιόν
Έστω ότι ο δρομέας είναι στη θέση όπου (ΚΔ) = 0,3 m τότε RΚΔ / RΚΛ = (ΚΔ) / (ΚΛ) => RΚΔ / 10 Ω = 0,3 m / 0,5 m => RΚΔ = 6 Ω και RΔΛ = 4 Ω
εφαρμόζουμε τον νόμο του Ohm στον μεγάλο βρόχο οπότε έχουμε : 2.Ε = i ( 2.r + RΚΛ ) =>
=> 2 . 12 V = i ( 2 . 1 Ω + 10 Ω ) => i = 24 / 12 Ω => i = 2 A η ένδειξη του αμπερομέτρου είναι 2 Α
στον βρόχο ΜΔΛΜ έχουμε : Ε = VMΔ + i ( r + RΔΛ ) => 12 V = VMΔ + 2 A ( 1 Ω + 4 Ω ) => 12 V - 10 V = VMΔ => VMΔ = 2 V η άνοδος έχει υψηλότερο δυναμικό από την κάθοδο
στον βρόχο ΜΚΔΜ έχουμε : Ε = i ( r + RΚΔ ) + VΔM => 12 V = 2 A ( 1 Ω + 6 Ω ) + VΔM => 12 V - 14 V = VΔM => VΔM = - 2 V => VMΔ = 2 V η άνοδος έχει υψηλότερο δυναμικό από την κάθοδο
Εάν προσπέσει ακτινοβολία με συχνότητα : f = 6.1014 Hz δηλαδή μήκος κύματος : λ = c / f = 3.108 m/s / 6.1014 Hz = 0,5.10-6 m = 5.10-7 m = 500 nm κάθε φωτόνιο έχει ενέργεια : Ε = h.f = 6,63.10-34 J.s 6.1014 Hz = 39,78.10-20 J = 4.10-19 J = 4.10-19 J / 1,6.10-19 C/e = 2,5 eV > 2,4 eV = φ οπότε h.f + e.VMΔ = Ke + φ => 2,5 eV + e. 2V = Ke + 2,4 eV => Ke = 2,1 eV = 2,1 1,6.10-19 J = 3,36.10-19 J κινητική ενέργεια των εξερχομένων από το μέταλλο ηλεκτρονίων όταν φθάνουν στην άνοδο
3,36.10-19 J = 0,5 9.10-31 kg u2 => u2 = 0,75.1012 => u = 0,86.106 m/s ταχύτητα των ηλεκτρονίων όταν φθάνουν στην άνοδο
ένα φωτόνιο ενέργειας Ε = hf = 4.10-19 J / 1,6.10-19 C/e = 2,5 eV προσπίπτει σε ένα ηλεκτρόνιο ενός ατόμου της μεταλλικής επιφάνειας και του "δίνει" όλη την ενέργειά του 2,5 eV επειδή το έργο εξαγωγής του μετάλλου δηλαδή το ποσό της ενέργειας για να εξέλθει το ηλεκτρόνιο από το άτομο είναι φ = 2,4 eV η διαφορά 0,1 eV είναι η κινητική ενέργεια του ηλεκτρονίου μόλις βγει από το άτομο αλλά επειδή υπάρχει διαφορά δυναμικού VMΔ = 2V μεταξύ ανόδου και καθόδου το ηλεκτρόνιο οδεύει προς την άνοδο κερδίζοντας ενέργεια από το ηλεκτρικό πεδίο e.VMΔ = e. 2V = 2 eV οπότε το ηλεκτρόνιο φθάνει στην άνοδο έχοντας ενέργεια 0,1 eV + 2 e V = 2,1 e V = Ke
Έστω φθάνουν Ν = 1012 ηλεκτρόνια στην άνοδο κάθε δευτερόλεπτο, το ρεύμα που διαρρέει το μίκροαμπερόμετρο είναι : i = N |qe|/ t = 1012 1,6.10-19 C/s = 1,6.10-7 A = 0,16 μΑ
Έστω η ένδειξη του μικροαμπερομέτρου είναι i = 4 μA = 4.10-6 A = N |qe|/ t = N 1,6.10-19 C / 1s => N = 2,5.1013 ηλεκτρόνια φθάνουν στην άνοδο εάν όλα τα εξερχόμενα ηλεκτρόνια από το μέταλλο φθάνουν στην άνοδο και για κάθε φωτόνιο της ακτινοβολίας αντιστοιχεί ένα ηλεκτρόνιο και το εμβαδόν της επιφάνειας της καθόδου είναι : Α=10-3m2 η ένταση της ακτινοβολίας είναι : Ι = P/Α = N.h.f / A.t = 2,5.1013 3,978.10-19 J / 10-3 m2 1s = 9,945.10-3 W/m2 = 0,01 W/m2 περίπου
L = 4 ∙ 𝜋 ∙ 10-7 108 20 10-4 / 0,16 ∙ 𝜋 = 0,5 H RΣ = 100 V2 / 20 W = 5 Ω
12 V = i 6 Ohm => i = 2 A iΣ = 20 W / 10 V = 2 A η συσκευή λειτουργεί κανονικά
L di/dt = i (R1 + RΣ) => 0,5 di/dt = 1 20 => di/dt = 40 A/s
U = 0,5 L i2 = 0,5 0,5 4 = 1 J
i2 R1 = 4 15 = 60 W i2 RΣ = 4 5 = 20 W 20 / 80 = 1/4 QΣ = 1/4 1 J = 0,25 J
h f + eV = Ke + φ => 6,6 10-34 6 1014 + 1,6 10-19 1 = Ke + 2,4 . 1,6 10-19 =>
=> 39,6 10-20 + 1,6 10-19 = Ke + 3,84 10-19 => 0,12 10-19 + 1,6 10-19 = Ke = 1,72 .10-19 J
h f + eV = Ke + φ => h f + e V0 = φ => 6,6 10-34 6 1014 + 1,6 10-19 V0 = 2,4 1,6 10-19 =>
=> 3,96 10-19 + 1,6 10-19 V0 = 3,84 10-19 => - 0,12 10-19 / 1,6 10-19 = V0 = - 0,12 / 1,6 V = - 0,075 V
f = c / λ = 3 108 / 5 10-7 = 0,6 1015 Hz = 6 1014 Hz V = φ/e - h/e f f0 = φ/e
h f + eV = Ke + φ => 6,6 10-34 6 1014 + eV = Ke + 6,25 . 1,6 10-19 =>
=> 39,6 10-20 + eV = Ke + 10 10-19 => 40 10-20 + eV = Ke + 10 10-19 => 4 10-19 + eV = Ke + 10 10-19 => - 6 10-19 + eV = Ke όση τάση και να βάλουμε τα ηλεκτρόνια δεν βγαίνουν από την επιφάνεια του λευκοχρύσου διότι η ακτινοβολία έχει μικρή συχνότητα για να βγουν ηλεκτρόνια από την επιφάνεια του λευκοχρύσου πρέπει η συχνότητα να είναι : h f0 = φ => f0 = φ / h = 6,25 1,6 10-19 / 6,6 10-34 => f0 = 1,5 1015 Hz λ0 = c / f0 = 3 108 / 1,5 1015 = 2 10-7 m = 200 10-9 m = 200 nm < 400 nm (ιώδες) πρέπει η ακτινοβολία να είναι υπεριώδης
ΘΕΜΑ Γ
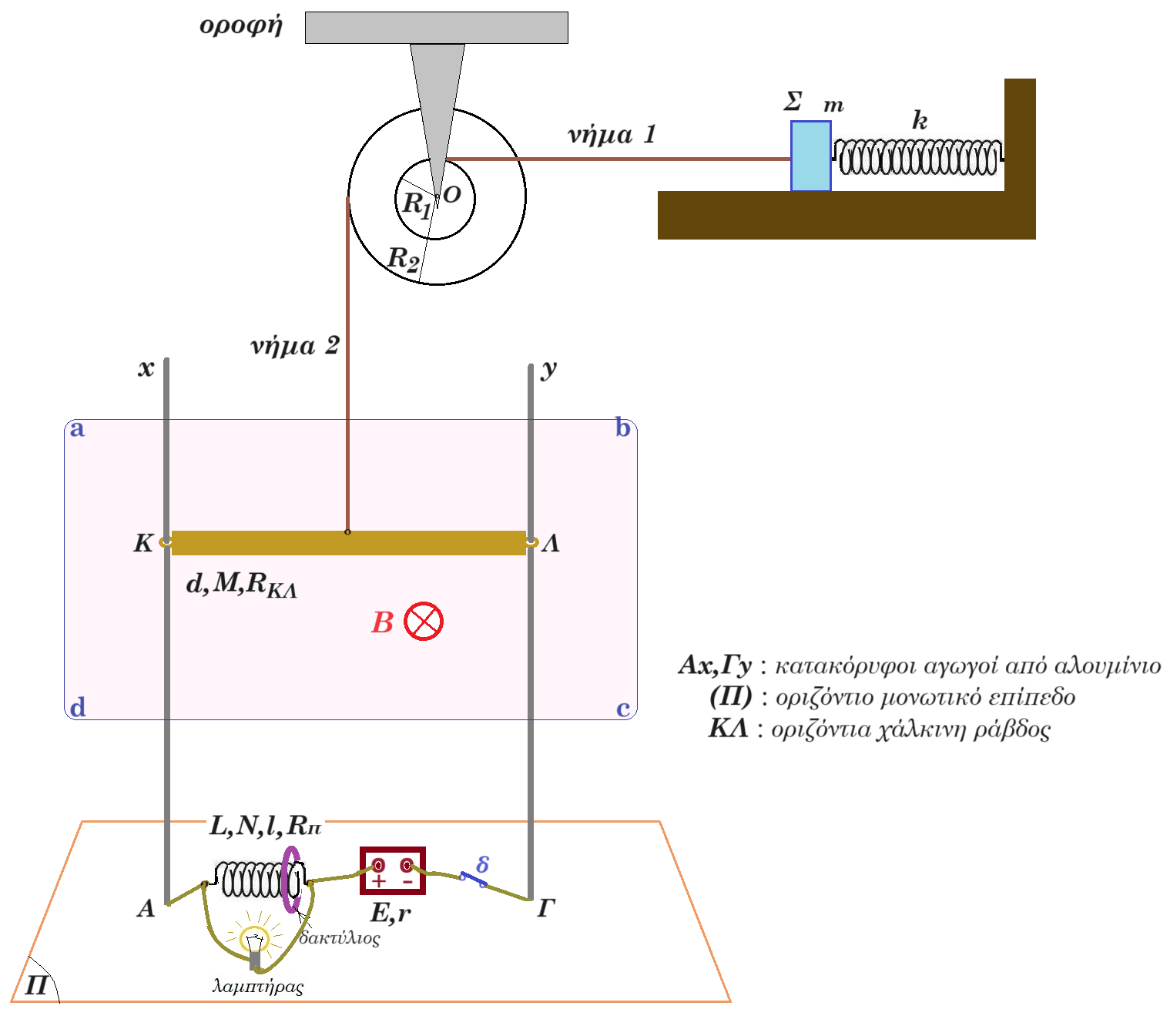
Στην κατακόρυφη διάταξη του σχήματος ο διακόπτης δ είναι κλειστός, τα σώματα βρίσκονται σε ισορροπία (ακίνητα). Το σώμα Σ έχει μάζα m = 0,6kg το ιδανικό ελατήριο έχει σταθερά k = 60 N/m η διπλή τροχαλία έχει ακτίνες R2 = 0,6 m R1 = 0,2 m είναι στερεωμένη στην οροφή η ράβδος ΚΛ έχει μάζα M = 0,5 kg μήκος d = 1 m ωμική αντίσταση RΚΛ = 3 Ω η ηλεκτρική πηγή συνεχούς ρεύματος έχει ηλεκτρεγερτική δύναμη E = 12 V εσωτερική αντίσταση r = 1 Ω το οριζόντιο ομογενές μαγνητικό πεδίο έχει ένταση B = 1 Tesla ο λαμπτήρας έχει ωμική αντίσταση Rλ = 12 Ω το πηνίο φέρει Ν = 100 σπείρες με εμβαδόν Απ = π.10-4 m2 για κάθε σπείρα, έχει μήκος l = 0,1 m ωμική αντίσταση Rπ = 6 Ω συντελεστή αυτεπαγωγής L = 0,4 Henry
Γ.1. Μετακινούμε λεπτό κλειστό κυκλικό δακτύλιο που έχει ωμική αντίσταση Rδ = 1 Ω και εμβαδόν επιφάνειας Αδ = 3,2.10-4 m2 από το άκρο του πηνίου έως το μέσον αυτού σε χρονικό διάστημα Δt = 1 ms. Εξηγείστε γιατί ο δακτύλιος διαρρέεται από ηλεκτρικό ρεύμα, βρείτε την ένταση του και σχεδιάστε την φορά του.
Τη στιγμή t = 0 ανοίγουμε τον διακόπτη δ και αφαιρούμε το νήμα 1.
Γ.2.α. Εκφράστε τον ρυθμό μεταβολής της κινητικής ενέργειας του σώματος Σ συναρτήσει του χρόνου και σχεδιάστε την συνάρτηση σε βαθμολογημένους άξονες.
Γ.2.β. Εκφράστε την δυναμική ενέργεια του ελατηρίου συναρτήσει της απομάκρυνσης του σώματος Σ από τη θέση ισορροπίας του και σχεδιάστε την συνάρτηση σε βαθμολογημένους άξονες.
Γ.3. Εάν κατά τη διάρκεια της κίνησης του σώματος Σ ενεργεί πάνω του δύναμη F με μέτρο ανάλογο της ταχύτητάς του αλλά αντίθετης κατεύθυνσης τότε το πλάτος ταλάντωσης μειώνεται κατά 20% της αρχικής του τιμής κατά τη διάρκεια της 1ης περιόδου.
Γ.3.α. στο τέλος της 1ης περιόδου η δύναμη επαναφοράς έχει μέτρο ίσο με :
Α. 10 Ν Β. 6 Ν Γ. 9,6 Ν Δ. 12 Ν
Γ.3.β. στη χρονική διάρκεια της 2ης περιόδου η απώλεια ενέργειας είναι :
Α. 11,52 J Β. 12,48 J Γ. 6,24 J Δ. 18,36 J
Γ.3.γ. στο τέλος της 3ης περιόδου η δύναμη του ελατηρίου έχει μέτρο ίσο με :
Α. 32,4 Ν Β. 41,2 Ν Γ. 48,6 Ν Δ. 54,8 Ν
Γ.4. Η τροχαλία στρέφεται με γωνιακή επιτάχυνση αγων = 20/3 rad/s2 ενώ η ράβδος κατέρχεται κατακόρυφα, τα άκρα της Κ, Λ είναι παντοτε σε επαφή με τους αγωγούς Αx και Γy. Εξηγείστε γιατί φορτίζεται η ράβδος και εκφράστε την τάση VΚΛ συναρτήσει του χρόνου.
Γ.5. Τη στιγμή t = 0 που ανοίγουμε τον διακόπτη δ ο ρυθμός μεταβολής της εντάσεως του ηλεκτρικού ρεύματος είναι : di/dt = - 45 Α/s Ο λαμπτήρας θα φωτοβολήσει εντονότερα; Εξηγείστε. Σχεδιάστε την ένταση του ρεύματος που διαρρέει το πηνίο από τη στιγμή t = 0 και μετά.
A.1. Τ = 20 10-6 s = 2 10-5 s f = 1/T = 0,5 105 Hz = 50 KHz A = 2 μm
A.2. L0 = 48cm L1 = 36cm A1 = 12cm L2 = 42cm A2 = 6cm A3 = 3cm A4 = 1,5m L4 = 48 - 1,5 = 46,5m
A.3. m g = k Δl => Δl = 10 / 100 = 0,1 m επιμήκυνση
Α0 = y = 1 m το ελατήριο είναι συσπειρωμένο κατά 1 m - 0,1 m = 0,9 m
A1 = 0,8 m |ΣF| = k A1 = 100 N/m 0,8 m = 80 N E1 = 0,5 k A12 = 0,5 100 0,82 = 32 J
A2 = 0,8 0,8 m = 0,64 m E2 = 0,5 k A22 = 0,5 100 0,642 = 20,48 J
E1 - E2 = 32 - 20,48 = 11,52 J
A3 = 0,8 0,64 m = 0,512 m πλάτος τότε το ελατήριο είναι συσπειρωμένο κατά 0,512 m - 0,1 m = 0,412 m η δύναμη του ελατηρίου θα είναι : 100 N/m 0,412 m = 41,2 N
A.4.
acm = 8 m/s2 = aγων R => aγων = 8 m/s2 / 0,5 m = 16 rad/s2
aκ = v2 / R = acm => v2 = 8 m/s2 0,5 m = 4 m2/s2 => v = 2 m/s = vcm = ω R
vA2 = vcm2 + ( ω R )2 = 22 + 22 => vA = 2√2 m/s
t = vcm / acm = 2 m/s / 8 m/s2 = 0,25 s
ΘΕΜΑ Γ
Ν = 100 σπείρες l = 0,1 m Rπ = 6Ω L = 0,18 Henry Rλ = 12Ω d = 1m M = 0,5kg RΚΛ = 3Ω B = 1Tesla r = 1Ω E = 12V m = 0,6 kg k = 60 N/m R2 = 0,6 m R1 = 0,2 m
ο διακόπτης δ κλειστός
Rπ,λ = Rπ Rλ / (Rπ + Rλ) = 6Ω 12Ω / ( 6Ω + 12Ω ) = 4Ω
Ε = i ( r + Rπ,λ + RΚΛ ) => 12 = i ( 1 + 4 + 3 ) => i = 1,5A iπ = 1A iλ = 0,5A
Bπ = μ0 iπ Ν/l = 4π 10-7 Ν/Α2 1Α 100 / 0,1m = 4π 10-4 Τ στο κέντρο του πηνίου
Βπ' = 2π 10-4 Τ στο άκρο του πηνίου
μαγνητική ροή Φαρχική = Βπ' Αδ = 2π 10-4 Τ 3,2 10-4 m2 = 6,4.π 10-8 Weber
Φτελική = Βπ Απ = 4π 10-4 Τ 3,2 10-4 m2 = 12,8.π 10-8 Weber
μεταβολή μαγνητικής ροής ΔΦ = 12,8.π 10-8 Wb - 6,4.π 10-8 Wb = 6,4.π 10-8 Wb
επαγωγική τάση Εεπαγ = - ΔΦ / Δt = - 6,4.π 10-8 Wb / 10-3 s = - 6,4.π 10-5 Volt
επαγωγικό ρεύμα iεπαγ = Εεπαγ / Rδ = - 6,4.π 10-5 V / 1 Ω = - 6,4.π 10-5 Α
λόγω της φοράς του ηλεκτρικού ρεύματος που διαρρέει το πηνίο η φορά του μαγνητικού πεδίου του πηνίου έχει κατεύθυνση οριζόντια προς τα δεξιά
από το άκρον του πηνίου έως το μέσον του η ένταση Βπ αυξάνεται οπότε ο δακτύλιος αντιδρά και διαρρέεται από επαγωγικό ρεύμα τέτοιας φοράς που το μαγνητικό πεδίο Βεπαγ που δημιουργεί τείνει να αναιρέσει την αύξηση του Βπ η κατεύθυνση του Βεπαγ είναι οριζόντια προς τα αριστερά
FL = B i d = 1T 1A 1m = 1 N δύναμη Laplace κατακόρυφη προς τα πάνω
βάρος ράβδου M g = 0,5 kg 10 m/s2 = 5 N κατακόρυφη προς τα κάτω
τάση νήματος Τ2 = 4 Ν κατακόρυφη προς τα πάνω
ισορροπία τροχαλίας Στ(Ο) = 0 => Τ2 R2 - T1 R1 = 0 => 4 0,6 - T1 0,2 = 0 => T1 = 12 N
ισορροπία Σ Τ1 = Fελατ = k Δl => 12 N = 60 N/m Δl => Δl = 0,2 m
ανοίγουμε τον διακόπτης δ και αφαιρούμε το νήμα 1 τη στιγμή t = 0
k = m ω2 => ω2 = k / m = 60 N/m / 0,6 kg => ω = 10 rad/s T = 2π/ω = 2π/10 = π/5 s
x(t) = 0,2 ημ(10.t + π/2) v(t) = 2 συν(10.t + π/2) a(t) = - 20 ημ(10.t + π/2)
dK/dt = m v a = 0,6 2 συν(10.t + π/2) [ - 20 ημ(10.t + π/2) ] =
= - 24 ημ(10.t + π/2) συν(10.t + π/2) = - 12 ημ(20.t + π) = + 12 ημ(20.t)
Uελατ = ½ k x2 = ½ 60 0,04 ημ2(10.t + π/2) = 1,2 [ 1 - συν(20.t + π) ] / 2 = 0,6 συν(20.t)
- 0,2 m £ x £ + 0,2 m T1 = 2π/20 = π/10 s
α. στο τέλος της 1ης περιόδου η δύναμη επαναφοράς έχει μέτρο ίσο με :
Α. 10 Ν Β. 6 Ν Γ. 9,6 Ν Δ. 12 Ν
Fεπαν = - k A1 = - k 80% A0 = - 60 N/m 0,8 0,2 m = - 9,6 N
β. στη χρονική διάρκεια της 2ης περιόδου η απώλεια ενέργειας είναι :
Α. 11,52 J Β. 12,48 J Γ. 6,24 J Δ. 18,36 J
A0 = 0,2 m A1 = 0,8 0,2 m = 0,16 m A2 = 0,8 0,16 m = 0,128 m A3 = 0,8 0,128 m = 0,01024 m
E0 = 0,5 k A02 = 0,5 60 0,22 = 1,2 J E1 = 0,5 60 0,162 = 0,768 J E2 = 0,5 60 0,1282 = 0,768 J ΔΕ = Ε1 - Ε0 = - 0,432 J
γ. στο τέλος της 3ης περιόδου η δύναμη του ελατηρίου έχει μέτρο ίσο με :
Α. 32,4 Ν Β. 41,2 Ν Γ. 48,6 Ν Δ. 54,8 Ν
η τροχαλία στρέφεται με γωνιακή επιτάχυνση αγων = 20/3 rad/s2 και η ράβδος κατέρχεται με επιτάχυνση α = αγων R2 = 20/3 rad/s2 0,6 m = 4 m/s2 v = a t = 4.t
Eεπαγ = Β v d = 1T 4.t 1m = 4.t = VΛΚ(t) VΚΛ(t) = - 4.t
- L di/dt = i (Rπ + Rλ) => di/i = - L/(Rπ + Rλ) dt => i(t) = I0 e- L/(Rπ + Rλ).t = 1 e- 0,4/18.t = e-t/45
- L di/dt = i (Rπ + Rλ) => - 0,4 ( - 45 ) = i (6 + 12) => i = 18 / 18 => i = 1 A > iλ = 0,5 A
όταν ο διακόπτης ήταν κλειστός ο λαμπτήρας διαρρεόταν από ρεύμα iλ = 0,5 A ενώ τη στιγμή που ανοίγουμε τον διακόπτη ο λαμπτήρας διαρρέεται από ρεύμα i = 1 A συνεπώς φωτοβολεί εντονότερα στιγμιαία και μετά αμυδρότερα και σβήνει
