ΘΕΜΑ Γ
Εγκάρσιο κύμα διαδίδεται κατά μήκος ενός ομογενούς ελαστικού μέσου με ταχύτητα υ=0,2m/s προς τη θετική κατεύθυνση. Τη χρονική στιγμή t=0 το σημείο Ο που βρίσκεται στη θέση x=0, ξεκινά ταλάντωση από τη θέση ισορροπίας με θετική ταχύτητα.  Σημείο Κ του μέσου που βρίσκεται στη θέση x_K=+2m τη χρονική στιγμή t=10,5s βρίσκεται για πρώτη φορά στην ακραία θέση της ταλάντωσής του και η απόσταση των ακραίων θέσεων της ταλάντωσής του είναι d=8cm.
Γ1.  Να γράψετε την εξίσωση του κύματος    [Μονάδες 5]
Γ2.  Κάποια χρονική στιγμή t1 που το σημείο Κ βρίσκεται στην θέση ισορροπίας της ταλάντωσής του κινούμενο προς την αρνητική κατεύθυνση, να βρεθεί η απομάκρυνση ταλάντωσης ενός σημείου Λ που
βρίσκεται στην θέση xΛ=2,3m, αν γνωρίζετε ότι αυτή τη χρονική στιγμή το σημείο Λ ήδη ταλαντώνεται για χρόνο Δt>T.    [Μονάδες 5]
Γ3.  Τη χρονική στιγμή t2 =2,5s να βρεθεί ο αριθμός των σημείων του μέσου που έχουν απομάκρυνση από τη θέση ισορροπίας y=-2cm    [Μονάδες 5]
Γ4.  Κάποια χρονική στιγμή που η απομάκρυνση του σημείου Κ από την θέση ισορροπίας είναι y=2cm να βρεθεί η επιτάχυνση ταλάντωσης του σημείου    [Μονάδες 5]
Γ5.  Να βρεθεί το μέτρο του μέγιστου ρυθμού μεταβολής της ορμής ενός σημείου του μέσου με μάζα m=10^-5 Κg      [Μονάδες 5]
Δίνεται η επιτάχυνση της βαρύτητας g=10m/s²   

Γ1.   d = 2A  => A = 4cm = 0,04 m  πλάτος ταλάντωσης σημείου Κ           t = x_K / v = 2m / 0,2m/s = 10s  

το κύμα θέλει χρόνο  10s  για να φθάσει στο Κ από την πηγή  οπότε  0,5s = Τ/4  =>  Τ = 2 s    οπότε  λ = υΤ = 0,2m/s  2s  =>  λ = 0,4m  μήκος κύματος       y = 0,04 ημ(2πt/2 - 2πx/0,4)  = 0,04 ημ(πt - 5πx) 

Γ2.    y_Κ = 0,04 ημ(πt₁ - 5πx_Κ) =>  0  =  0,04 ημ(πt₁ - 10π) =>  0 =  0,04 ημ(πt₁) =>  πt₁ = Νπ      

  υ_Κ =  0,04π συν(πt₁) < 0  =>  συν(Νπ)  <  0   =>  Ν = 1, 3, 5,  ...   άρα  συν(πt₁) = συν(Νπ) = -1

  y_Λ = 0,04 ημ(πt₁ - 5πx_Λ) =  0,04 ημ(πt₁ - 5π 2,3) =                                            ημ(11,5π) = - 1             

       =  0,04 ημ(πt₁)  συν(5π 2,3)  -  0,04 συν(πt₁)  ημ(5π 2,3) =  -  0,04 (- 1) ημ(11,5π)  = - 0,04 m

Γ3.    t = 2,5s   x = v t = 0,2 m/s  2,5 s =  0,5 m  

y = 0,04 ημ(πt₂ - 5πx) => - 0,02 = 0,04 ημ(2,5π - 5πx) => - 0,02 = 0,04 συν(5πx) => συν(5πx) = - ½   =>  5πx =  2Νπ + 2π/3   =>  0  <  x =  2Ν/5 + 2/15  <  0,5 m  => 

 => - 2/15  < 2N/5  < 0,5 - 2/15 =  (15 - 4) / 30 = 11/30  =>  - 5/2 2/15 < N < 5/2 11/30 => 

  =>  - 1/3  <  N < 11/12     N = 0    x = 2/15 m

  ή    5πx =  2Νπ + 4π/3   =>  0  <  x =  2Ν/5 + 4/15  <  0,5 m  => 

  => - 4/15  <  2N/5  < 0,5 - 4/15 =  (15 - 8) / 30 = 7/30  =>  - 4/15 5/2  < N < 5/2 7/30 =>

  =>   - 2/3  < N < 7/12     N = 0    x = 4/15 m

Γ4.     y_Κ = 0,04 ημ(πt₁ - 5πx_Κ) = 0,02  =>  a_Κ =  - 0,04π² ημ(πt₁ - 5πx_Κ) =  - 0,02 π² = - 0,2 m/s²  

Γ5.    dp/dt  =  ΣF = m a =  10^-5 (- 0,04π² ) ημ(πt - 5πx)       |dp/dt|_max = 4.π² 10^-7 N  »  4 10^-6 N 

ΘΕΜΑ Δ

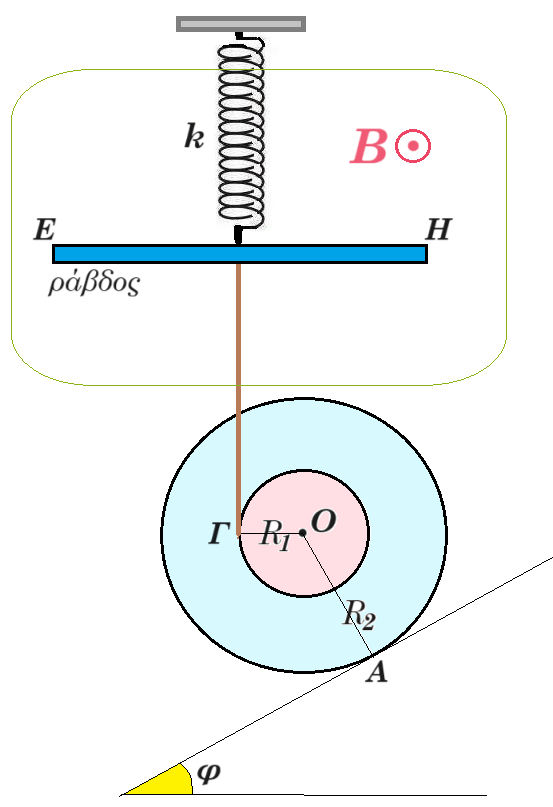
Στη διάταξη του σχήματος όλα τα σώματα βρίσκονται στο ίδιο κατακόρυφο επίπεδο και ισορροπούν.  Το κεκλιμένο επίπεδο είναι τραχύ και έχει γωνία κλίσης φ=30°.  Το στερεό έχει μάζα Μ=2Kg και αποτελείται από δύο συγκολλημένους ομοαξονικούς δίσκους με ακτίνες R1 και R2 =2R1.  Γύρω από τον δίσκο (1) έχει τυλιχθεί αβαρές μη εκτατό νήμα το ελεύθερο άκρο του οποίου είναι δεμένο στο μέσον της λεπτής ομογενούς ράβδου ΕΗ μάζας m=1Kg και μήκους  l = 0,4m.  Η ράβδος είναι στερεωμένη στην μία άκρη του ιδανικού ελατηρίου σταθεράς k=100Ν/m η άλλη άκρη του οποίου είναι στερεωμένη σε οροφή.  Το νήμα συμπίπτει με τον άξονα του ελατηρίου και είναι κατακόρυφο.  Στον χώρο που βρίσκεται το ελατήριο με την ράβδο υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης  Β=0,5Τ.  Δίνεται g=10m/s2

Δ1. Να δείξετε ότι η τάση του νήματος είναι Τ=10Ν.   [Μονάδες 5]
Την t=0 το νήμα κόβεται με αποτέλεσμα η ράβδος να αρχίσει A.A.T. με D=k και το στερεό να κυλίεται χωρίς ολίσθηση στο κεκλιμένο επίπεδο με σταθερή επιτάχυνση αcm =4m/s².
Δ2. α)  Να γράψετε την εξίσωση της ταχύτητας ταλάντωσης της ράβδου σε συνάρτηση με το χρόνο (θεωρώντας θετική φορά προς τα κάτω)    [Μονάδες 5]
      β)  Οταν η διαφορά δυναμικού μεταξύ των σημείων Ε και Η είναι V_E - V_H = 0,2 V για πρώτη φορά να βρεθεί ο ρυθμός μεταβολής της βαρυτικής ενέργειας της ράβδου.   [Μονάδες 5]
Δ3.  Να γίνει η γραφική παράσταση της δύναμης του ελατηρίου συναρτήσει της απομάκρυνσης.     [Μονάδες 5]
Δ4.  Να βρεθεί η χρονικη στιγμή που  N_ταλ = Ν_στερ  αν δίνεται R2=0,2m  όπου Νταλ  ο αριθμός των ταλαντώσεων  και  Νστερ  ο αρθμός περιστροφών του στερεού. 

Δ1.

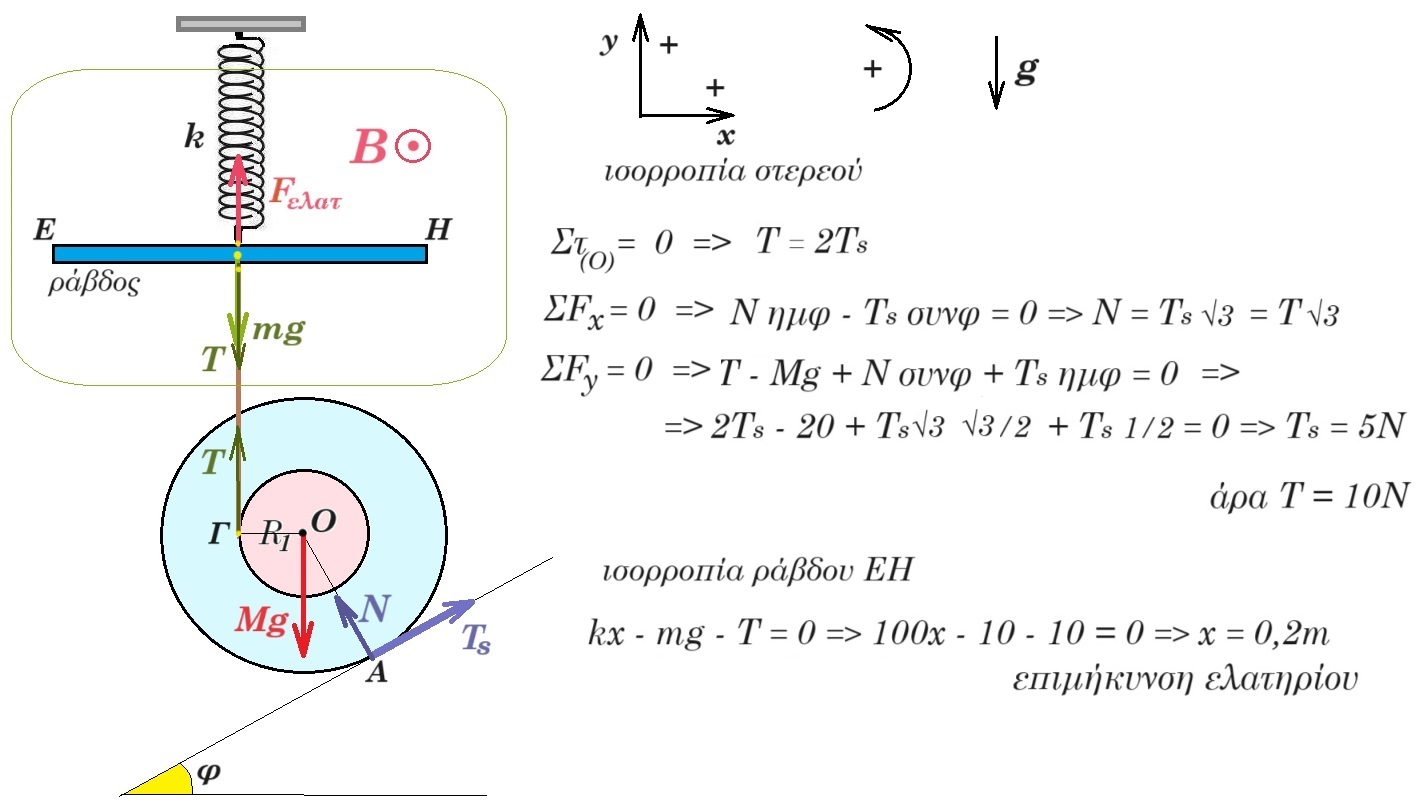
Δ2.   ισορροπία ράβδου - ελατηρίου :  mg = k Δl  =>  10 = 100 Δl  =>  Δl = 0,1 m   

 A = 0,2m - 0,1m = 0,1m   πλάτος ταλάντωσης ράβδου   

 k = m ω²  =>  100 = 1 ω²  => ω = 10 rad/s     f = ω/2π = 5/π Hz       T = 2π/ω = 2π/10 = π/5 s 

   x(t) = 0,1 ημ(10.t + π/2)     v(t) = 1 συν(10.t + π/2)          α(t) =  - 10 ημ(10.t + π/2) 

    V_EH = B l v = 0,5 T  0,4 m  συν(10.t + π/2)  = 0,2 συν(10.t + π/2)  

τη στιγμή t₀ = 0   η ράβδος βρίσκεται  0,2m - 0,1m = 0,1m   χαμηλότερα από τη θέση ισορροπίας της κατά την ταλάντωσή της  και αρχίζει να κινείται προς τα πάνω,  λόγω της κατεύθυνσης του μαγνητικού πεδίου Β  τα ηλεκτρόνια της δέχονται δύναμη Lorentz  και κινούνται προς το άκρο Ε  που φορτίζεται αρνητικά  ενώ το άκρο της Η  φορτίζεται θετικά  έτσι η τάση  V_EH  είναι αρνητική  έως ότου η ράβδος πάει στο άνω άκρο της ταλάντωσης   ( οπότε όταν διέρχεται από την θέση ισορροπίας είναι : V_EH = - 0,2 V )  καθώς κινείται προς κάτω όταν διέρχεται από την θέση ισορροπίας είναι : V_EH = + 0,2 V   ο χρόνος που πέρασε είναι  Τ/2 + Τ/4 = 3/4 Τ =  3/4 2π/ω = 3/4 2π/10 = 3π/20 s 

 v(t) = 1 συν(10.t + π/2)  =  1 συν(10.3π/20 + π/2)  =  1 συν(3π/2 + π/2) = συνπ = - 1 m/s

ο ρυθμός μεταβολής της βαρυτικής ενέργειας είναι :  dU_{βαρυτική} / dt = mg v = 10 N (-1 m/s) = -10 J/s

Δ3.

ΣF = m a  => mg + F_ελατ = m a  =>  10 + F_ελατ = - 10 ημ(10.t + π/2) =>  F_ελατ = - 10 - 10 ημ(10.t + π/2) 

   F_ελατ = - 10  - 100.x  = - 100 (0,1 + x)  = - k (Δl + x)        - 0,1 m  £  x  £  + 0,1 m

   t = 0    x = + 0,1m = +A          t = T/4 = π/20 s     x = 0          t = T/2 = π/10 s     x = - 0,1m = -A  

Δ2.   κύλιση στερεού :  ΣF_x = m a_cm  =>  Mg ημ30°  -  Τ_τρ.ολ. = m a_cm  => 20 Ν  0,5  -  Τ_τρ.ολ. =  2 kg  4 m/s²  => Τ_τρ.ολ. = 2 N   δύναμη τριβής ολισθήσεως    

  Ν_ταλ =  f t  =  5/π t  

 Ν_στερ =  θ / 2π =  ½  α_γων t² / 2π  =  ½  (α_cm / R₂) t² / 2π  =  ½  (4 / 0,2) t² / 2π  =  20 t² / 4π = 5/π t² 

 Ν_ταλ = Ν_στερ  => 5/π t  =  5/π t²  =>  t = 1 s