47. Στο διπλανό σχήμα βλέπου μια διπλή τροχαλία με δύο δίσκους ακτίνων R και 2R αντιστοίχως η οποία μπορεί να περιστρέφεται γύρω από σταθερό άξονα που διέρχεται από το κέντρο της Ο. Και έναν τροχό κέντρου K μάζας m, ακτίνας R που μπορεί να κυλίεται χωρίς να ολισθαίνει σε οριζόντιο επίπεδο. Νήμα μη εκτατό που δεν ολισθαίνει στα αυλάκια τυλίγεται στο μικρό δίσκο της τροχαλίας και άλλο όμοιο νήμα στο μεγάλο δίσκο και στον τροχό. 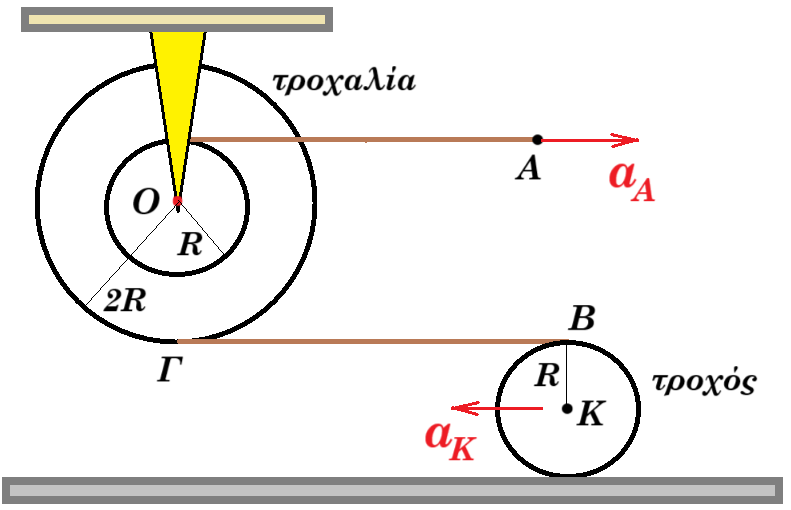 Το άκρο Α επιταχύνεται με την επίδραση δύναμης με σταθερή επιτάχυνση αΑ. Αν σε χρόνο Δt=t, το κέντρο μάζας του τροχού K μετατοπιστεί κατά ΔxΚ , τότε από την τροχαλία θα έχει ξετυλιχτεί μήκος ℓ. Για τα ΔxK και ℓ ισχύει η σχέση
Το άκρο Α επιταχύνεται με την επίδραση δύναμης με σταθερή επιτάχυνση αΑ. Αν σε χρόνο Δt=t, το κέντρο μάζας του τροχού K μετατοπιστεί κατά ΔxΚ , τότε από την τροχαλία θα έχει ξετυλιχτεί μήκος ℓ. Για τα ΔxK και ℓ ισχύει η σχέση
(α) ΔxK=ℓ (β) ΔxK=2ℓ (γ) ΔxK= ℓ
αΒ = 2 αΚ aA = αγων,τροχαλία R αΒ = αΓ = αγων,τροχαλία 2R = 2 aA
xK = 0,5 aK t2 l = R θ = R 0,5 αγων,τροχαλία t2 = 0,5 aA t2 = xA
aK = aB / 2 = aA => xK = xA = l
48. Στο κύκλωμα το πηνίο έχει συντελεστή αυτεπαγωγής L και αντίσταση R2=R, ο αντιστάτης έχει αντίσταση R1=3R και ο ευθύγραμμος αγωγός ΚΛ αμελητέα αντίσταση. Αρχικά ο διακόπτης δ είναι ανοικτός και ο αγωγός ΚΛ κινείται χωρίς τριβές με σταθερή ταχύτητα υ έχοντας πάντα επαφή με τις παράλληλες αγώγιμε ράγες αμελητέας αντίστασης στα Κ και Λ. Όλη η διάταξη είναι μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο εντάσεως Β.  Κάποια χρονική στιγμή κλείνουμε το διακόπτη δ και ασκούμε στον ΚΛ κατάλληλη δύναμη F παράλληλη στις δύο ράγες ώστε να συνεχίσει να κινείται με την ίδια σταθερή ταχύτητα, υ. Σε χρονική διάρκεια Δt1=6L/R εκλύεται από τον αντιστάτη R1 ποσό θερμότητας Q1 και στο τέλος αυτής της χρονικής διάρκειας το ρεύμα σταθεροποιείται σε όλους τους κλάδους του κυκλώματος.
Κάποια χρονική στιγμή κλείνουμε το διακόπτη δ και ασκούμε στον ΚΛ κατάλληλη δύναμη F παράλληλη στις δύο ράγες ώστε να συνεχίσει να κινείται με την ίδια σταθερή ταχύτητα, υ. Σε χρονική διάρκεια Δt1=6L/R εκλύεται από τον αντιστάτη R1 ποσό θερμότητας Q1 και στο τέλος αυτής της χρονικής διάρκειας το ρεύμα σταθεροποιείται σε όλους τους κλάδους του κυκλώματος.
Ι. Η απόλυτη τιμή του ρυθμού μεταβολής του ρεύματος στον κλάδο του πηνίου τη στιγμή που κλείσαμε το διακόπτη είναι
α. Βυℓ/2L β. Βυℓ/L γ. Βυℓ/3L
II. Στο τέλος της χρονικής διάρκειας Δt1 ανοίγουμε το διακόπτη και μετά από χρόνο Δt2 το ρεύμα στον κλάδο του πηνίου μηδενίζεται. Στη διάρκεια Δt2 εκλύθηκε στον αντιστάτη R1 ποσό θερμότητας Q1´ που είναι ίσο με
(α) 3Q1/16 (β) 3Q1/4 (γ) Q1/2
στα άκρα της ράβδου ΚΛ επάγεται τάση Εεπαγ = B l v
όταν κλείσουμε τον διακόπτη δ : Εεπαγ = B l v = i1 R1 = L di2/dt + i2 R2 FL = B l (i1 + i2)
F - FL = m a = 0 διότι υ = σταθερή άρα F = B l (i1 + i2)
τη στιγμή που κλείνουμε τον διακόπτη i2 = 0 δεν διέρχεται ρεύμα από το πηνίο διότι εμφανίζεται στα άκρα του τάση αυτεπαγωγής οπότε Εεπαγ = B l v = i1 R1 = L di2/dt => di2/dt = B l v / L (β)
η ταχύτητα της ράβδου είναι σταθερή σε χρόνο Δt1 = 6L/R διανύει διάστημα Δx1 = v 6L/R
το έργο που παράγει η F γίνεται θερμότητα πάνω στις αντιστάσεις οι οποίες συνδέονται παράλληλα R1,2 = R 3R / 4R = 3R/4 συνολική αντίσταση και αποθηκεύεται ενέργεια στο πηνίο
όταν σταθεροποιείται το ρεύμα στους κλάδους : i1 = Blv / R1 = Blv / 3R i2 = Blv / R2 = Blv / R
i = i1 + i2 = 4Blv / 3R στο πηνίο αποθηκεύεται ενέργεια : UL = 0,5 L i22 = L B2l2v2 / 2R2
Q1 = i12 R1 Δt1 = ( B2l2v2 / 9R2 ) 3R 6L/R = 2 B2l2v2 L / R2
η ενέργεια του πηνίου καταναλώνεται πάνω στις αντιστάσεις επειδή R1 = 3R και R2 = R τότε Q1' = 3 Q2' οπότε UL = Q1' + Q2' = Q1' + Q1'/3 = 4Q1'/3 => Q1' = 3/4 L B2l2v2 / 2R2 = 3LB2l2v2 / 8R2
Q1' / Q1 = 3/16
Β.1. Δύο ελαστικές σφαίρες Σ1, Σ2 με μάζες m1=m και m2=6m συνδέονται με νήμα μήκους ℓ και τοποθετούνται σε λείο
οριζόντιο επίπεδο σε αρχική απόσταση d όπου d<ℓ. Βλήμα μάζας m κινούμενο οριζόντια με ταχύτητα υ0 καρφώνεται στο σώμα m1 ακαριαία. Όταν η απόσταση μεταξύ του συσσωματώματος και του m2 γίνει ℓ το νήμα τεντώνει στιγμιαία χωρίς το σύστημα να χάσει ενέργεια. Μετά οι σφαίρες συγκρούονται κεντρικά και ελαστικά και αποκτούν ταχύτητες, V1 η Σ1 και V2 η Σ2. Θετική θεωρείται η φορά προς τα δεξιά. Για τις ταχύτητες ισχύει Q
α) V1 = - υ0/4 V2 = υ0/4 β) V1 = - υ0/8 V2 = 3υ0/8 γ) V1 = υ0/2 V2 = 0
m v0 = 2m v1 => v1 = v0 / 2
2m v0 / 2 = 2m V1 + 6m V2 => v0 = 2V1 + 6V2
0,5 2m v02/ 4 = 0,5 2m V12 + 0,5 6m V22 => v02/ 4 = V12 + 3 V22 =>
=> v02/ 4 = ( v0 / 2 - 3V2 )2 + 3 V22 => v02/ 4 = v02/ 4 - 2 v0 / 2 3V2 + 9V22 + 3V22 =>
=> 0 = - 3v0 V2 + 12V22 => 3V2 ( 4V2 - v0 ) = 0 => V2 = 0 ή V2 = v0 / 4
εάν V2 = v0 / 4 το Σ2 κινείται προς τα δεξιά τότε V1 = v0 / 2 - 3V2 = v0 / 2 - 3 v0 / 4 = - v0 / 4 το Σ1 κινείται προς τα αριστερά η λύση απορρίπτεται
εάν V2 = 0 τότε V1 = v0 / 2 η λύση είναι δεκτή
Β.2. H ρόδα του σχήματος «σύρεται» με τη βοήθεια νήματος από τη δύναμη F. Αν η γωνία θ είναι μικρή η ρόδα στρέφεται προς τα αριστερά. Όταν η γωνία θ είναι μεγάλη η ρόδα στρέφεται προς τα δεξιά. Αν ο συντελεστής τριβής είναι μ και το βάρος της ρόδας (w), υπολογίστε το μέτρο της δύναμης F για την οποία η ρόδα θα γλιστρήσει για την «κρίσιμη» γωνία θ.
Δίνεται R=2r.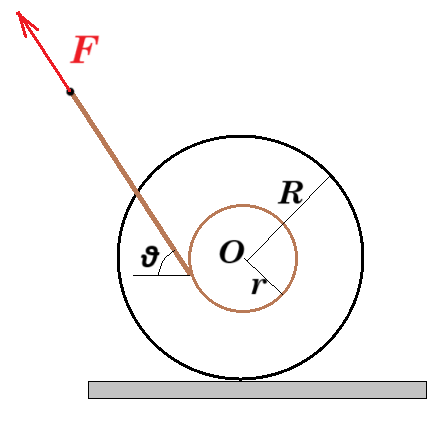
α) F = μ w / (0,5 + μ ημθ) β) F = μ w / (0,5 + μ συνθ) γ) F = (μ+1) w / (0,5 + μ ημθ)
N - mg + F ημθ = 0 T 2r - F r = 0 => 2T = F
Τ = μ Ν => ½ F = μ ( mg - F ημθ ) => ½ F - μ mg + μ F ημθ = 0 => F = μ mg / (0,5 + μ ημθ)
Β.3. Μια δέσμη φωτονίων έχει ισχύ P, μήκος κύματος λ και μεταφέρει n1 φωτόνια ανά sec. Αν μια άλλη δέσμη ισχύος 2P με μήκος κύματος λ/2 μεταφέρει n2 φωτόνια ανά sec τότε ισχύει :
α. n1=n2 β. n1=2n2 γ. n2=2n1
Ρ = Ε / t = N1 hf / t = n1 h c / λ 2Ρ = Ε / t = N2 hf / t = n2 h c / (λ/2)
διαιρώντας κατά μέλη : 1/2 = n1 / λ / n2 / (λ/2) = n1 / λ / 2n2 / λ = n1 / 2n2 => n1 = n2
Β.4. Εκτοξεύουμε τη μεταλλική ράβδο ΚΛ μάζας m, ωμικής αντίστασης, R με αρχική ταχύτητα υ0 με τον τρόπο που φαίνεται στο σχήμα μέσα σε ομογενές μαγνητικό πεδίο, Β. Οι τριβές της ράβδου με τις παράλληλες ράγες είναι αμελητέες. Tα άκρα Α και Γ των δύο ραγών συνδέονται με αντιστάτη αντίστασης 3R.
I. Η θερμότητα Joule που εκλύεται στoν αντιστάτη 3R που γεφυρώνει τις ράγες, μέχρι η ράβδος να έχει το 20% της αρχικής της κινητικής ενέργειας είναι:
α. W = 0,2mυ02 β. W = 0,5mυ02 γ. W = 0,3mυ02
ΙΙ. Το φορτίο που μετατοπίζεται μέσα στο κύκλωμα μέχρι η ράβδος να χάσει το 80% της αρχικής της ταχύτητάς είναι
(α) q = 0,2mυ0 / Βℓ (β) q = Βℓ / 0,8mυ0 (γ) q = 0,8mυ0 / Βℓ
Κτελ = 0,2 Καρχ => ½ m v2 = 0,2 ½ m v02 => v2 = 0,2 v02
Καρχ = Κτελ + W => W = 0,8 Καρχ = 0,8 ½ m v02 = 0,4 m v02 = WR + W3R WR + 3 WR = 4 WR => WR = 0,1 m v02 => W3R = 0,3 m v02
σε χρόνο Δt η ράβδος χάνει το 80% της αρχικής της ταχύτητας άρα Δp = m v - m v0 = m 0,2 v0 - m v0 = - 0,8 m v0
στον χρόνο Δt διέρχεται φορτίο Δq από το κύκλωμα i = Δq / Δt
ΣF = FL = B l i => Δp / Δt = B l Δq / Δt => Δp = B l Δq => 0,8 m v0 = B l Δq =>
=> Δq = 0,8 m v0 / Bl
Β.5. Μια πηγή αρμονικής διαταραχής Ο βρίσκεται στην αρχή του άξονα διάδοσης Οx του κύματος και έχει x0=0. Το κύμα διαδίδεται κατά τη θετική φορά του άξονα. Το σημείο Ο ταλαντώνεται με εξίσωση απομάκρυνσης, y=Αημ(ωt). Κάποια χρονική στιγμή t σημείο Μ του άξονα Οx βρίσκεται στη θέση yΜ=+Α. Την ίδια στιγμή άλλο σημείο Λ του ίδιου άξονα του οποίου η φάση προηγείται της φάσης του Μ κατά 5π/3 rad θα βρίσκεται σε θέση:
α. y+0 β. y=+Α γ. y=+Α/2
φΜ = ωt + 2πxΜ /λ φΑ = ωt + 2πxΑ /λ φΑ = φΜ + 5π/3
Δχ/λ = Δφ/2π = 5π/3 / 2π => Δχ/λ = 5/6
yM = A ημ(φΜ) = +Α => ημ(φΜ) = 1 => ημ( φΑ - 5π/3 ) = 1 =>
=> ημ(φΑ) συν(5π/3) - συν(φΑ) ημ(5π/3) = 1 => ημ(φΑ) 1/2 - συν(φΑ) (-3½ /2) = 1 =>
=> ημ(φΑ) + 3½ συν(φΑ) = 1
ημ2(φΑ) + συν2(φΑ) = 1 => 1 + 3χ2 - 2 3½ χ + χ2 = 1 => χ = 0 ή χ = 1/2.3½
ημ(φΑ) = 1 - 3½ 1/2.3½ = 1 - 1/2 = 1/2 άρα yΑ = A ημ(φΑ) = +Α 1/2 = + Α/2
Β.6. Στο σύστημα του σχήματος βλέπουμε το σώμα μάζας m1 συνδεδεμένο με το ελατήριο σταθεράς k1 και το σώμα μάζας m2 με το ελατήριο σταθεράς k2 με που ηρεμεί πάνω σε λείο οριζόντιο επίπεδο.  Δίνονται ότι m1=m2=m και ο συντελεστής οριακής τριβής μ μεταξύ των δύο σωμάτων και η σχέση των
Δίνονται ότι m1=m2=m και ο συντελεστής οριακής τριβής μ μεταξύ των δύο σωμάτων και η σχέση των
σταθερών k1=3k και k2=k. Βάζουμε το σύστημα σε οριζόντιες ταλαντώσεις.
I. Αν το σώμα m1 δεν ολισθαίνει πάνω στο σώμα m2 τότε η περίοδος της ταλάντωσης του συστήματος είναι
(α) Τ= 2π√(𝑚/𝑘) (β) Τ= 2π√(𝑚/2𝑘) (γ) Τ= 2π√(2𝑚/k)
ΙΙ. Οι τιμές του πλάτους Α της ταλάντωσης για τις οποίες το ένα σώμα δεν ολισθαίνει πάνω στο άλλο είναι
(α) Α < 2μmg/k (β) Α < μmg /4k (γ) Α < μmg / k
για τυχαία μετατόπιση χ προς τα δεξιά τα σώματα δέχονται ομόρροπες δυνάμεις από τα ελατήρια F1 + F2 = - k1 x - k2 x = - (k1 + k2) x = - 4k x => D = 4k
ω2 = D / (m1 + m2) = 4k / 2m = 2k/m => ω = √(2k/m) = 2π/Τ => Τ = 2π√(m/2k)
για το Σ1 Τ - k1 x > 0 => μ mg - k A > 0 => A < μmg / k
Β.7. Στο κύκλωμα η πηγή και το πηνίο είναι ιδανικά δηλαδή χωρίς ωμική αντίσταση, οι τρεις λαμπτήρες είναι όμοιοι και έχουν ο καθένας αντίσταση R. 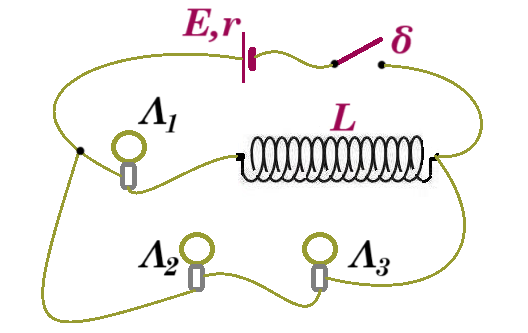 Tη χρονική στιγμή t=0 κλείνει ο διακόπτης δ. Τη χρονική στιγμή t1 που ο ρυθμός αποταμίευσης της ενέργειας μαγνητικού πεδίου στο πηνίο είναι ΔU/Δt=E2/4R τότε
Tη χρονική στιγμή t=0 κλείνει ο διακόπτης δ. Τη χρονική στιγμή t1 που ο ρυθμός αποταμίευσης της ενέργειας μαγνητικού πεδίου στο πηνίο είναι ΔU/Δt=E2/4R τότε
α. ο λαμπτήρας Λ1 φωτοβολεί πιο έντονα από τους άλλους
β. όλοι φωτοβολούν το ίδιο.
γ. oι λαμπτήρες Λ2 και Λ3 φωτοβολούν πιο έντονα από τον Λ1.
E = i1 R + L di1/dt = i2 2R i2 = E / 2R
dU/dt = L i1 di1/dt = E2 / 4R => i1 ( E - i1 R ) = E2 / 4R => R i12 - E i1 + E2/4R = 0
Δ = Ε2 - 4 R E2/4R = 0 i1 = - β / 2α = - ( - Ε ) / 2R = E / 2R = i1
επειδή οι εντάσεις των ρευμάτων στους κλάδους έχουν την ίδια τιμή όλοι οι λαμπτήρες φωτοβολοούν το ίδιο
Β.9. Σε ένα πείραμα φωτοηλεκτρικού φαινομένου όταν η ισχύς της φωτεινής δέσμης είναι P1 ο ρυθμός των φωτονίων Ν/t και το μήκος κύματος λ1 μόλις που εξέρχονται φωτοηλεκτρόνια από τη μεταλλική πλάκα. Tο πείραμα επαναλαμβάνεται με την ίδια μεταλλική πλάκα και ακτινοβολία ισχύος P2=1,25P1 αλλά με το ίδιο ρυθμό φωτονίων Ν/t και μήκος κύματος λ2.
Ι. Tότε για τα μήκη κύματος ισχύει α. λ2=λ1 β. λ2=0,8λ1 γ. λ2=0,6λ1
ΙΙ. Η κινητική ενέργεια των εξερχομένων φωτοηλεκτρονίων στο δεύτερο πείραμα θα είναι ίση με
α. το 20% της ενέργειας της προσπίπτουσας ακτινοβολίας
β. το 40% της ενέργειας της προσπίπτουσας ακτινοβολίας
γ. το 60% της ενέργειας της προσπίπτουσας ακτινοβολίας
Ρ1 = Ε / t = N/t h c / λ1 P2 = 1,25 Ρ1 = Ε / t = N/t h c / λ2
διαιρώντας κατά μέλη : 1 / 1,25 = λ2 / λ1 => λ2 = λ1 / 1,25 = 0,8 λ1
h c / λ1 = φ ( Κe = 0 ) => λ1 = h c / φ λ2 = 0,8 h c / φ
h c / λ2 = φ + Κe => φ / 0,8 = φ + Κe => Ke = 0,25 φ = φ / 4
h c / λ2 = φ / 0,8 Ke / ( h c / λ2 ) = φ/4 / φ/0,8 = 0,8 / 4 = 0,2 20%
Β.10. Τα άκρα μιας χορδής μήκους L=2m είναι στερεωμένα σε ακλόνητα σημεία. Δύο κύματα που διαδίδονται στη χορδή με μήκος κύματος λ=0,5m συμβάλουν και δημιουργούν στάσιμο κύμα.
Ι. Ο αριθμός των δεσμών ( μαζί με τα άκρα ) που έχουν δημιουργηθεί πάνω στη χορδή είναι:
α. 5 β. 7 γ. 9
ΙΙ. Αν η ταχύτητα διάδοσης των κυμάτων είναι υ=103 m/s και δημιουργούνται συνολικά 6 δεσμοί πάνω στην ίδια χορδή ( μαζί με τα άκρα ) τότε η τιμή της συχνότητας με την οποία ταλαντώνεται η χορδή πρέπει να είναι:
α. 1000Ηz β. 1250Ηz γ. 1500Ηz
αριθμός ατράκτων (αριθμός κοιλιών) L = N λ/2 => 2m = N 0,5m/2 => N = 8
αριθμός δεσμών = 9
αριθμός δεσμών = 6 άρα 5 κοιλίες L = N λ/2 => 2m = 5 λ/2 => λ = 0,8 m
v = λ f => 1000 m/s = 0,8 m f => f = 1250 Hz
Β.11. Οι σφαίρες που φαίνονται στο σχήμα συγκρούονται μετωπικά και ελαστικά.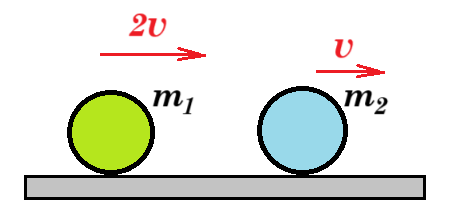
Ι. Αν είναι m1 = m2, το ποσοστό της κινητικής ενέργειας της σφαίρας m1 που μεταβιβάζεται στη σφαίρα m2 είναι:
α. 50% β. 75% γ. 90%
ΙΙ. Αν το ποσοστό της κινητικής ενέργειας της μάζας m1 που μεταφέρεται στη σφαίρα m2 είναι 96% τότε η σχέση των μαζών είναι:
α. m2 = 2m1 β. m2 = 3m1 γ. m2 =4m1
v1' = 2 v m / 2m = v v2' = 2 2v / 2m = 2v ανταλλάσσουν ταχύτητες
Κ1 = ½ m 4v2 Κ1' = ½ m v2 K1' - K1 = - 3 ½ m v2 = - 3/4 K1 ποσοστό 75%
Κ1' - Κ1 = - 0,96 Κ1 => Κ1' = 0,04 Κ1 => ½ m (v1')2 = 0,04 ½ m v12 => (v1')2 = 0,04 v12 =>
=> v1' = 0,2 v1 = 0,2 2v = 0,4v ή v1' = - 0,2 v1 = - 0,4v
εάν v1' = 0,4 v => 2v (m1 - m2) / (m1 + m2) + 2 v m2 / (m1 + m2) = 0,4 v =>
=> (m1 - m2) / (m1 + m2) + m2 / (m1 + m2) = 0,2 => m1 - m2 + m2 = 0,2 (m1 + m2) =>
=> m1 = 0,2 m1 + 0,2 m2 => 0,8 m1 = 0,2 m2 => 4 m1 = m2 δεκτή λύση
εάν v1' = - 0,4 v => 2v (m1 - m2) / (m1 + m2) + 2 v m2 / (m1 + m2) = - 0,4 v =>
=> (m1 - m2) / (m1 + m2) + m2 / (m1 + m2) = - 0,2 => m1 - m2 + m2 = - 0,2 (m1 + m2) =>
=> m1 = - 0,2 m1 - 0,2 m2 => 1,2 m1 = - 0,2 m2 => 6 m1 = - m2 αδύνατον
B.12. H μεταλλική ράβδος ΚΛ μάζας m, αμελητέας ωμικής αντίστασης μπορεί να κινείται με τα άκρα της σε δύο οριζόντιες αγώγιμες ράγες αμελητέας αντίστασης που συνδέονται με αντιστάτη R με τον τρόπο που φαίνεται στο σχήμα. Όλο το σύστημα βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο, Β. Αρχικά είναι ακίνητη. Ασκούμε στο μέσον
Όλο το σύστημα βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο, Β. Αρχικά είναι ακίνητη. Ασκούμε στο μέσον
της ράβδου ΚΛ σταθερή δύναμη F ίση με το βάρος mg της ράβδου. Στην πρώτη περίπτωση δεν υπάρχουν τριβές και η ΚΛ αποκτάει κάποια στιγμή οριακή ταχύτητα υ1=υ0. Στη δεύτερη περίπτωση υπάρχουν τριβές της ράβδου με τις ράγες με
συντελεστή τριβής μ και με την ίδια δύναμη F=mg η ράβδος αποκτάει οριακή ταχύτητα υ2=0,6υ0.
Ο συντελεστής τριβής είναι
(α) μ=0,2 (β) μ=0,6 (γ) μ=0,4
Blv = iR => i = Blv/R F - Bli = m a => F - B2l2v/R = m a a = 0 => v1 = mgR / B2l2 = v0 (1)
Blv = iR => i = Blv/R F - T - Bli = m a => F - μmg - B2l2v/R = m a
a = 0 => v2 = (mg - μmg)R / B2l2 = 0,6v0 (2)
(1) , (2) => (mg - μmg)R / B2l2 = 0,6 mgR / B2l2 => 1 - μ = 0,6 => μ = 0,4
Β.13. Στο σχήμα (1) το σώμα Σ2 που είναι δεμένο με το ελατήριο σταθεράς k ταλαντώνεται έτσι ώστε το σώμα Σ2να ανασηκώνεται από το έδαφος. Στο σχήμα (2) το σώμα Σ2είναι τοποθετημένο πάνω στο Σ1 και το σύστημα ταλαντώνεται έτσι ώστε το Σ2να μην εγκαταλείπει το Σ1. Αν Α1 και Α2 είναι τα οριακά πλάτη ώστε να γίνονται αυτές οι ταλαντώσεις
με τις συνθήκες που περιγράφονται τότε
Ι. Για τα πλάτη ισχύει η σχέση
| (α) Α1=Α2 |
(β) Α1>Α2 |
(γ) Α1<Α2 |
| ΙΙ. Για τις μέγιστες ταχύτητες ταλάντωσης ισχύει η σχέση: |
| (α) υ01=υ02 |
(β) υ01>υ02 |
(γ) υ01<υ02 |
Β.14. Το τρακτέρ κινείται σε οριζόντιο δρόμο με σταθερή ταχύτητα και οι τροχοί κυλίονται χωρίς να ολισθαίνουν. Oι μεγάλοι έχουν ακτίνα R και οι μικροί ακτίνα r. Η σχέση των ακτίνων των τροχών είναι R=7r/4. Τη χρονική στιγμή t1 δύο
σημεία Κ και Λ των τροχών βρίσκονται ταυτόχρονα σε επαφή με το έδαφος. Τη χρονική στιγμή t2 τα ίδια σημεία βρίσκονται για πρώτη φορά και πάλι ταυτόχρονα σε επαφή με το έδαφος. Στο χρονικό διάστημα Δt=t2-t1 το όχημα έχει
μετατοπιστεί κατά
(α) 8πR (β) 6πR (γ) 9,5πR
vK = ωΚ R = vτρακτέρ vΛ = ωΛ r = vτρακτέρ
άρα ωΚ R = ωΛ r = ωΛ 4R/7 => 7 ωΚ = 4 ωΛ => 7 fΚ = 4 fΛ => 7 N1/t = 4 N2/t => 7 N1 = 4 N2
χΚ = 2πR Ν1 χΛ = 2πr N2 = 2π 4R/7 N2 = 4/7 2πR Ν2 = 2πR Ν1 = χΚ
για 1η φορά Ν1 = 4 στροφές Ν2 = 7 στροφές τότε χΚ = 2πR Ν1 = 8πR
Β.15. Αντιστάτης διαρρέεται από περιοδικά μεταβαλλόμενο ρεύμα περιόδου Τ, του οποίου η ένταση μεταβάλλεται με το χρόνο, όπως στο διάγραμμα: 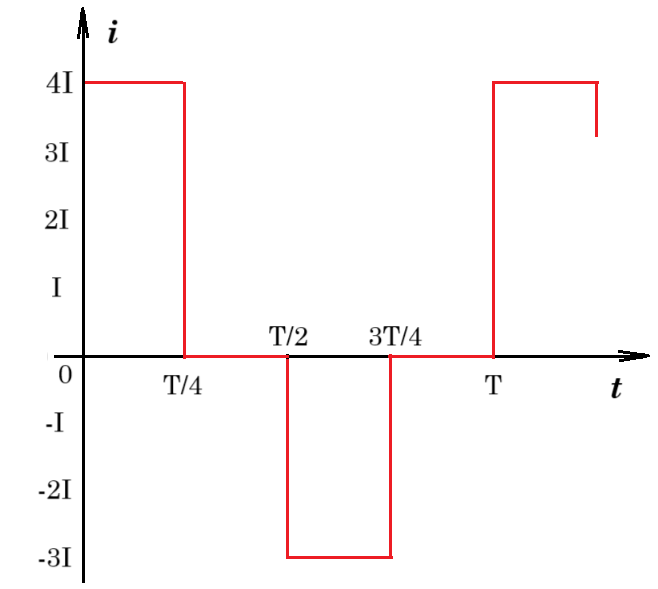
Ι. Η ενεργός ένταση του ρεύματος ισούται με:
(α) 5/2 I (β) √2/2 I (γ) 5√2/2 I
ΙΙ. Το φορτίο που μετατοπίζεται σε χρονικό διάστημα από 0 έως Τα είναι
(α) q=I∙T/4 (β) q= 3I∙T/4 (γ) q= - I∙T/4
Q = 16I2∙R∙T/4 + 9I2∙R∙T/4 = iεν2∙R∙T => iεν2 = 25Ι2 / 4 => iεν = 5Ι/2
q = 4I ∙ T/4 + (-3I) ∙ T/4 = i ∙ T/4
Β.16. Σε ένα πείραμα με το φωτοηλεκτρικό φαινόμενο, μία μονοχρωματική ακτίνα φωτός προσπίπτει σε μία μεταλλική πλάκα Α όπως φαίνεται στο παρακάτω σχήμα.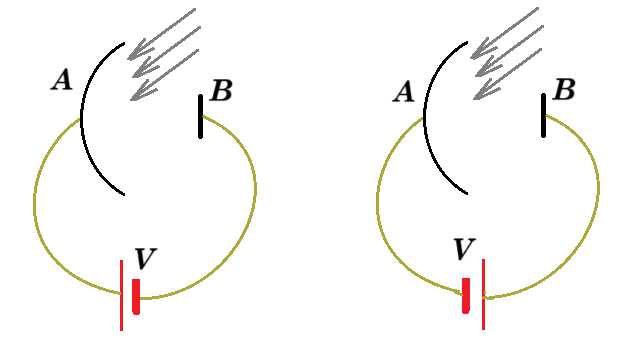 Παρατηρήθηκε ότι όταν η τάση ήταν V = 5V, με την πολικότητα που φαίνεται στο σχήμα αριστερά, η μέγιστη κινητική ενέργεια των φωτοηλεκτρονίων που χτυπούσαν στην πλάκα Β ήταν 1eV.
Παρατηρήθηκε ότι όταν η τάση ήταν V = 5V, με την πολικότητα που φαίνεται στο σχήμα αριστερά, η μέγιστη κινητική ενέργεια των φωτοηλεκτρονίων που χτυπούσαν στην πλάκα Β ήταν 1eV.
Όταν αντιστράφηκε η πολικότητα της πηγής και διπλασιάστηκε η συχνότητα των φωτονίων που προσπίπτουν στην μεταλλική πλάκα Α, παρατηρήθηκε ότι η κινητική ενέργεια των ηλεκτρονίων που χτυπούσαν την πλάκα Β ήταν μεταξύ 5eV και 20eV. Με βάση αυτά τα δεδομένα, το έργο εξαγωγής του μετάλλου στην πλάκα Α είναι:
(α) ϕ = 3eV (β) ϕ = 1eV (γ) ϕ = 5eV
h f + V e = Ke + φ => h f - 5V e = 1 eV + φ (1)
h f + V e = Ke + φ => h 2f + 5V e = Ke + φ (2)
(2) - 2*(1) => 15 eV = Ke - 2 eV - φ => Ke = 17 eV + φ
5 eV < 17 eV + φ < 20 eV => - 12 eV < φ < 3 eV
εάν φ = 1 eV Ke = 17 eV + φ = 18 eV < 20 eV
εάν φ = 3 eV Ke = 17 eV + φ = 20 eV μέγστη κινητική ενέργεια ηλεκτρονίων δεκτή λύση
εάν φ = 5 eV Ke = 17 eV + φ = 23 eV > 20 eV
παρατήρηση : 5 eV έχουν κινητική ενέργεια εκείνα τα ηλεκτρόνια τα οποία εξέρχονται με μηδενική κινητική ενέργεια από το μέταλλο Α και πέρνουν ενέργεια 5 eV από το ηλεκτρικό πεδίο μεταξύ των πλακών Α και Β
Β.17. Σε χορδή που είναι στερεωμένη μόνο στο ένα άκρο της συμβάλλουν δύο κύματα με μήκος κύματος λ=2m και παράγεται στάσιμο κύμα. Στο ελεύθερο άκρο της χορδής δημιουργείται κοιλία.
Ι. Το ελάχιστο μήκος της χορδής για να είναι δυνατή η δημιουργία στάσιμου κύματος είναι:
α. L=1m β. L=2m γ. L=0,5m
ΙΙ. Αν η χορδή είναι L=8,5m και το λ=2m σχηματίζονται συνολικά:
α. 8 δεσμοί β. 7 δεσμοί γ. 9 δεσμοί
L = λ/4 = 0,5 m ελάχιστο μήκος χορδής κ δ κ δ κ δ κ δ κ δ κ δ κ δ κ δ κ δ
L = λ/4 + Ν λ/2 => 8,5 = 0,5 + Ν 1 => Ν = 8 άτρακτοι 9 δεσμοί
Β.18. Η σφαίρα Α μάζας m συγκρούεται με ταχύτητα υ με την αρχικά ακίνητη σφαίρα, Β, μάζας 2m. Η κρούση θεωρείται ελαστική. Μετά την κρούση η σφαίρα Α κινείται κάθετα στην αρχική της διεύθυνση
με ταχύτητα VA και η Β με ταχύτητα VB υπό γωνία φ ως προς τον άξονα xx'.
Ι. Για τη γωνία φ ισχύει
α. φ=30° β. φ=45° γ. φ=60°
ΙΙ. Για τις ταχύτητες μετά την κρούση ισχύει:
α. VΑ=VΒ=υ β. VΑ=VΒ=υ √3/3 γ. VΑ=υ/2, VΒ=υ √(3/8)
m v = 2m VB,x => VB,x = v/2 0 = m VA + 2m VB,y => VA = - 2 VB,y
VB2 = VB,x2 + VB,y2 = v2/4 + VA2/4
0,5 m v2 = 0,5 m VA2 + 0,5 2m VB2 => v2 = VA2 + 2 VB2 => v2 = VA2 + v2/2 + VA2/2 =>
=> v2/2 = 3 VA2/2 => VA = v / √3
VB2 = VB,x2 + VB,y2 = v2/4 + VA2/4 = v2/4 + v2 / 12 = v2 / 3 => VB = v / √3
VA = - 2 VB,y => VB,y = - v / 2√3 εφθ = VB,y / VB,x = (- v / 2√3 ) / ( v / 2 ) = - 1/√3 => θ = -30°
Β.19. Κυκλικός αγωγός ακτίνας α και με αντίσταση ανά μονάδα μήκους R* , βρίσκεται σε οριζόντιο επίπεδο, εντός ομογενούς μαγνητικού πεδίου έντασης Β με διεύθυνση κάθετη στη σελίδα, της οποίας το μέτρο μεταβάλλεται με τον χρόνο σύμφωνα με τη σχέση B=B0 -λt ( λ: θετική σταθερά) Ο κυκλικός αγωγός διαρρέεται από επαγωγικό ρεύμα με φορά αντίθετη από τη φορά των δεικτών του ρολογιού, όπως φαίνεται στο παρακάτω σχήμα: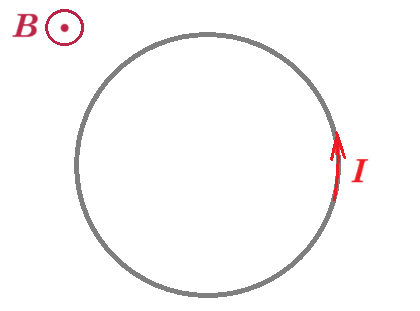 Η ένταση του επαγωγικού ρεύματος που διαρρέει τον αγωγό έχει τιμή:
Η ένταση του επαγωγικού ρεύματος που διαρρέει τον αγωγό έχει τιμή:
α) Ι = λα / 2R* β) Ι = λπα / 2R* γ) Ι = λα / R*
R = R* 2πα Φ = Β Α = (Β0 - λt) π α2 => ΔΦ/Δt = - λ π α2
I = Eεπαγ / R = - ΔΦ/Δt / R = λ π α2 / R* 2πα = λ α / 2R*
4√5
B.21. To σώμα Σ2 μάζας m2=3kg συνδέεται μέσω ελατηρίου σταθεράς k=100N/m με άλλο σώμα Σ1 μάζας m1=1kg που είναι δεμένο στο άνω άκρο του ελατηρίου.
Το σύστημα αρχικά ισορροπεί πάνω σε οριζόντιο επίπεδο. Θέτουμε το σώμα Σ1 σε κατακόρυφες ταλαντώσεις και θεωρούμε ως θετική τη φορά προς τα πάνω.
Δίνεται g=10m/s2 . Η σχέση που δίνει τη δύναμη Ν που δέχεται το Σ2 από το επίπεδο με την απομάκρυνση x του Σ1 από τη θέση ισορροπίας του είναι
(α) Ν=40-100x (β) Ν = 20-100x (γ) Ν= -40 -100x
ΙΙ. Για ποιες τιμές του πλάτους της ΑΑΤ το Σ2 δεν χάνει την επαφή του με το πάτωμα
(α) Α<0,2m (β) Α≤0,4m (γ) Α<0,4m
ισορροπία Σ1 : m1 g = k Δl => 10 = 100 Δl => Δl = 0,1 m συσπείρωση (-)
ω2 = k / m1 => ω = 10 rad/s F = - k (x + Δl) = - 100 (x - 0,1) = 10 - 100.x για το Σ1
το Σ2 δέχεται από το ελατήριο δύναμη F' = - 10 + 100.x
N - m2 g + F' = 0 => N - 30 + 100.x - 10 = 0 => N = 40 - 100.x
N ³ 0 => 40 ³ 100.x => x £ 0,4 m
B.22. Ακτίνα Χ με μήκος κύματος λ=3h/2mc σκεδάζει σε ακίνητο ηλεκτρόνιο με αποτέλεσμα η γωνία σκέδασης να είναι φ=90°. H κινητική ενέργεια του ηλεκτρονίου μετά τη σκέδαση.
α. Κ=m∙c2/3 β. Κ=m∙c2/15 γ. Κ=4m∙c2/15
λ' = 3h/2mc + h/mc = 5h/2mc
Ke = hc / (3h/2mc) - hc / (5h/2mc) = 2mc2/3 - 2mc2/5 = 4mc2/15
Β.23. H ράβδος ΚΛ αμελητέας αντίστασης αφήνεται να κινηθεί χωρίς τριβές κατά μήκος των δύο κατακόρυφων αγωγών αμελητέας αντίστασης σε χώρο που υπάρχει ομογενές μαγνητικό πεδίο έντασης Β1 με την κατεύθυνση οριζόντια προς τα μέσα. Οι αγωγοί συνδέονται με αντίσταση R. Μετά από διάστημα h αποκτάει οριακή ταχύτητα υ1 και στη συνέχεια εισέρχεται σε έναν άλλο χώρο όπου συνυπάρχουν δύο μαγνητικά πεδία. Το μαγνητικό πεδίο Β1 και ένα ακόμα με ένταση Β2=3Β1 αλλά με φορά αντίθετη του Β1. Μετά από κάποιο διάστημα η ΚΛ αποκτάει ταχύτητα υ2 τη στιγμή που έχει επιτάχυνση μέτρου α=g. Οι ταχύτητες υ1 και υ2 συνδέονται με τη σχέση
α. υ2=υ1/2 β. υ2=υ1/3 γ. υ2=υ1/4
B l v = i R FL = Bli = B2l2v/R mg - B2l2v/R = m a a = 0 => v = mgR / B2l2 = v1
2B l v = i R FL = 2Bli = 4B2l2v/R ισχυρότερο μαγνητικό πεδίο η δύναμη Laplace επιβραδύνει τη ράβδο
mg - 4B2l2v2 /R = m a = m (-g) => 2mg = 4B2l2v2 /R => v2 = mgR / 2B2l2 v2 = v1 / 2
B.24. Μια πηγή φωτός μήκους κύματος 𝜆 φωτίζει ένα μέταλλο από το οποίο εξέρχονται φωτοηλεκτρόνια με μέγιστη κινητική ενέργεια 1 𝑒𝑉. Μια δεύτερη πηγή φωτός με μήκος κύματος 𝜆/2 όταν φωτίζει το ίδιο μέταλλο προκαλεί την εκπομπή φωτοηλεκτρονίων μέγιστης κινητικής ενέργειας 4𝑒𝑉. Το έργο εξαγωγής 𝜑 του μετάλλου είναι:
(α) 3 𝑒𝑉 (β) 𝟐 𝒆𝑽 (γ) 4 𝑒𝑉
hf = 1eV + φ (1) h 2f = 4eV + φ (2)
(2) - 2*(1) => 0 = 2eV - φ => φ = 2eV
B.27. Η μπάλα μάζας m1=2kg εκτοξεύεται οριζόντια με ταχύτητα υ1=3m/s από την άκρη του οχήματος μάζας m2=4kg που φαίνεται στο σχήμα. 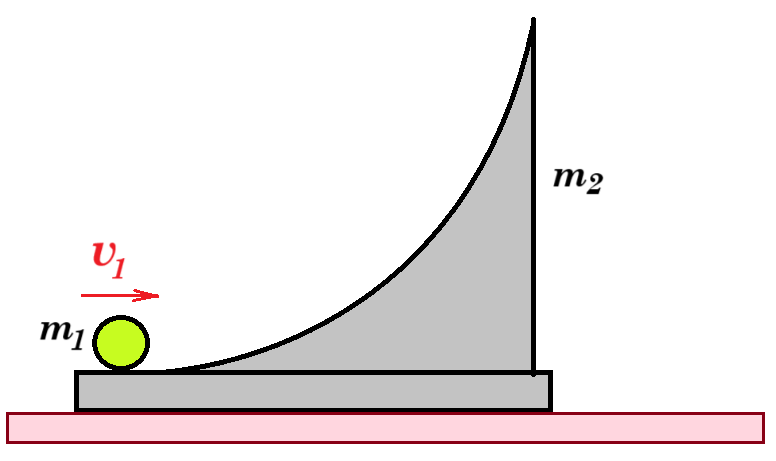 Η μπάλα ανεβαίνει χωρίς τριβές στο όχημα ολισθαίνοντας και φτάνει σε μέγιστο ύψος h χωρίς να χάσει την επαφή του με αυτό. Την ίδια στιγμή το όχημα έχει αποκτήσει ταχύτητα, V πάνω στο λείο οριζόντιο επίπεδο.
Η μπάλα ανεβαίνει χωρίς τριβές στο όχημα ολισθαίνοντας και φτάνει σε μέγιστο ύψος h χωρίς να χάσει την επαφή του με αυτό. Την ίδια στιγμή το όχημα έχει αποκτήσει ταχύτητα, V πάνω στο λείο οριζόντιο επίπεδο.
Ι. Το μέγιστο ύψος που φτάνει η μπάλα πάνω από το σημείο που εκτοξεύτηκε είναι
(α) h=0,2m (β) h=0,3m (γ) h=0,4m
II. Στη συνέχεια η μπάλα κατεβαίνει και εγκαταλείπει το όχημα με ταχύτητα V1 που είναι:
(α) V1=-1m/s (β) V1=-2m/s (γ) V1=-0,5m/s
m1 v1 = (m1 + m2) u => 2 3 = 6 u => u = 1 m/s δεξιά
½ m1 v12 = ½ (m1 + m2) u2 + m1 g h => 2 32 = 6 12 + 2 20 h => 18 = 6 + 40 h => h = 0,3 m
m1 v1 = (m1 + m2) u = m1 V1 + m2 V2 => 2 3 = 2 V1 + 4 V2 => V1 + 2V2 = 3
½ m1 v12 = ½ (m1 + m2) u2 + m1 g h = ½ m1 V12 + ½ m2 V22 => 2 32 = 2 V12 + 4 V22 =>
=> 9 = V12 + 2 V22 => 9 = 9 - 2 3 2V2 + 4V22 + 2V22 => 6V22 - 12V2 = 0 =>
=> V2 = 0 ή V2 = 2 m/s
εάν V2 = 0 τότε V1 = 3 m/s αδύνατον
εάν V2 = 2 m/s τότε V1 = - 1 m/s δεκτή λύση
B.28. Στο κύκλωμα που φαίνεται στο σχήμα, η πηγή είναι ιδανική με ΗΕΔ Ε, ο αντιστάτης έχει αντίσταση R1= R, το πηνίο αντίσταση R2=3R και ο συντελεστής αυτεπαγωγής του πηνίου είναι L. Ο μεταγωγός Μ είναι αρχικά κλειστός στην επαφή α και το ρεύμα στο κύκλωμα έχει αποκατασταθεί στη μέγιστη τιμή του. Μεταφέρουμε την χρονική στιγμή t=0 τον μεταγωγό στη θέση b.
Μεταφέρουμε την χρονική στιγμή t=0 τον μεταγωγό στη θέση b.
I. Η θερμότητα Joule που εκλύεται στην αντίσταση R1 από τη στιγμή t=0 μέχρι το μηδενισμό του ρεύματος είναι:
(α) LE2 / 64R2 (β) LE2 / 32R2 (γ) LE2 / 128R2
II. To μέτρο του ρυθμού μεταβολής του ρεύματος τη χρονική στιγμή t1 που έχει παραχθεί στους
αντιστάτες θερμότητα ίση με τα ¾ της ενέργειας του μαγνητικού πεδίου του πηνίου είναι
(α) di/dt=Ε/2L (β) di/dt=E/L (γ) di/dt= E/4L
Ε = i 4R UL = 0,5 L i2 = 0,5 L E2/16R2 = LE2/32R2 η αποθηκευμένη ενέργεια στο πηνίο γίνεται θερμότητα Joule πάνω στις αντιστάσεις LE2/32R2 = QR + Q3R = 4 QR => QR = LE2/128R2
αφού στους αντιστάτες έχει παραχθεί θερμότητα ίση με τα 3/4 της ενέργειας του πηνίου στο πηνίο θα έχει μείνει το 1/4 της ενέργείας του : 0,5 L i2 = 1/4 LE2/32R2 => i2 = E2/64R2 => i = E/8R
κλείστό κύκλωμα : L di/dt = i 4R => L di/dt = E/8R 4R => di/dt = E/2L
B.29. Δύο σύγχρονες πηγές κυμάτων βρίσκονται στα σημεία A και B μιας ευθείας x'x πάνω στην επιφάνεια υγρού και εκπέμπουν κύματα με μήκος κύματος λ=2m. Η απόσταση των δύο πηγών είναι ΑΒ=d=6,2m. Οι απομακρύνσεις των πηγών από τη θέση ισορροπίας τους δίνονται από τη σχέση y=Αημωt.
Ι. Το πλήθος των σημείων του ευθυγράμμου τμήματος AB που ταλαντώνονται με μέγιστο πλάτος (κοιλίες) είναι:
α. 8 σημεία β. 7 σημεία γ. 9 σημεία
ΙΙ. Το πλήθος των σημείων του ευθυγράμμου τμήματος AB που παραμένουν ακίνητα (δεσμοί), είναι:
α. 8 σημεία β. 7 σημεία γ. 6 σημεία
δεσμοί : χ = Ν λ/2 + λ/4 0 < χ < 6,2 => 0 < Ν 1 + 0,5 < 6,2 => -0,5 < Ν < 5,7 => Ν = 0, 1, 2, 3, 4, 5 6 δεσμοί
κοιλίες : 2πχ/λ = Νπ => χ = Ν λ/2 0 £ χ £ 6,2 => 0 £ Ν 1 £ 6,2 => 0 £ Ν £ 6,2 => Ν = 0, 1, 2, 3, 4, 5, 6 7 κοιλίες
B.30. Πρωτόνιο p και σωμάτιο α, (ma=4mp και qa=2qp) επιταχύνονται από την ηρεμία από την ίδια τάση V και αποκτούν ταχύτητες πολύ μικρότερες της ταχύτητας του φωτός. Η αβεβαιότητα σtη μέτρηση της θέσης για κάθε σωματίδιο είναι ίση με το μήκος κύματος de Broglie του κάθε σωματιδίου. Τότε ο λόγος της ελάχιστης τιμής της αβεβαιότητας στη μέτρηση της ορμής του σωματίου α προς την ελάχιστη τιμή της αβεβαιότητας στη μέτρηση της ορμής του πρωτονίου είναι ίσος με
α. 2√2 β. 2 γ. 1/2
qp V = Kp = pp2 / 2mp => qp V = pp2 / 2mp => pp2 = 2 qp V mp λp = h / pp
qa V = Ka = pa2 / 2ma => 2 qp V = pa2 / 8mp => pa2 = 16 qp V mp λa = h / pa
pa2 / pp2 = 16 qp V mp / 2 qp V mp = 8 => pa / pp = 2√2
B.31. Οι όμοιες σφαίρες Α και Β έχουν ίσες μάζες m1=m2=m και κινούνται μεταφορικά σε λείο οριζόντιο επίπεδο με ταχύτητες μέτρων υ1=υ2=υ. Τα κέντρα μάζας των σφαιρών Α και Β κινούνται αντίστοιχα στους ορθογώνιους άξονες y και x. 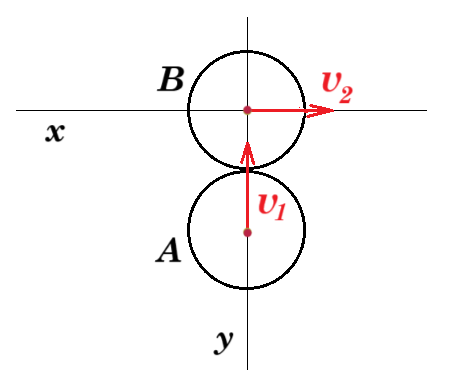 Τη στιγμή της σύγκρουσης των δύο σφαιρών η δύναμη που ασκεί η μία στην άλλη είναι κάθετη στην επιφάνεια επαφής τους. Η κρούση θεωρείται ελαστική. Μετά την κρούση τα κέντρα μάζας των σφαιρών Α και Β έχουν ταχύτητες με μέτρα V1, V2 για τις οποίες ισχύει
Τη στιγμή της σύγκρουσης των δύο σφαιρών η δύναμη που ασκεί η μία στην άλλη είναι κάθετη στην επιφάνεια επαφής τους. Η κρούση θεωρείται ελαστική. Μετά την κρούση τα κέντρα μάζας των σφαιρών Α και Β έχουν ταχύτητες με μέτρα V1, V2 για τις οποίες ισχύει
α. V1=υ, με γωνία θ=45° ως προς τον άξονα x και V2=0.
β. V1=υ και V2=υ με αντίθετες κατευθύνσεις πάνω στον άξονα y.
γ. V2=υ√2 με γωνία θ=45° ως προς τον άξονα x και V1=0.
η σφαίρα Β κινείται πάνω στον άξονα x οπότε ως προς τον άξονα y θεωρείται ακίνητη ( v2,y = 0 ) και δέχεται δύναμη F από τη σφαίρα Α πάνω στον άξονα y επειδή οι σφαίρες είναι όμοιες ανταλλάσσουν ταχύτητες δηλαδή η σφαίρα Α ακινητοποιείται V1 = v2,y = 0 , V2,y = v1 = v πάνω στον άξονα y
η σφαίρα Β κινείται πάνω στον άξονα x δεν δέχεται δύναμη από τη σφαίρα Α πάνω στον άξονα x οπότε συνεχίζει με την ίδια ταχύτητα δηλαδή : V2,x = v2 = v
τελικά V1 = 0 , V22 = V2,x2 + V2,y2 = v2 + v2 = 2 v2 => V2 = υ√2
εφθ = V2,y / V2,x = υ / υ = 1 => θ = 45° (γ)
B.32. Η μαγνητική ροή που διέρχεται μέσα από σωληνοειδές πηνίο Ν=10 σπειρών μεταβάλλεται με τον τρόπο που φαίνεται στο διάγραμμα Φ=f(t). 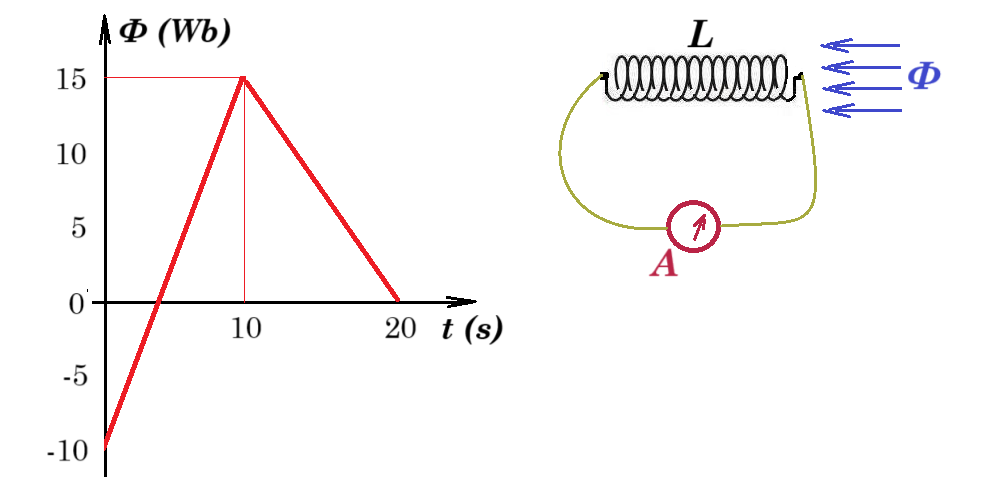 Το κλειστό κύκλωμα του πηνίου παρουσιάζει συνολική ωμική αντίσταση R=10Ω. Αφού σχεδιάσετε τη γραφική παράσταση μεταβολής της έντασης του επαγωγικού ρεύματος σε σχέση με το χρόνο υπολογίστε το φορτίο που μετατοπίζεται μέσα στο κύκλωμα από 0 έως 20s. Αυτό είναι
Το κλειστό κύκλωμα του πηνίου παρουσιάζει συνολική ωμική αντίσταση R=10Ω. Αφού σχεδιάσετε τη γραφική παράσταση μεταβολής της έντασης του επαγωγικού ρεύματος σε σχέση με το χρόνο υπολογίστε το φορτίο που μετατοπίζεται μέσα στο κύκλωμα από 0 έως 20s. Αυτό είναι
(α) q=0 (β) q=-10C (γ) q=10C
Φ(t) = 2,5.t - 10 [0 , 10s] Επαγ = - Ν ΔΦ/Δt = - 10 2,5 = - 25 V i = Εεπαγ / R = - 2,5 A
Φ(t) = - 1,5.(t-10) + 15 [10s , 20s] Επαγ = - Ν ΔΦ/Δt = - 10 (-1,5) = +15 V i = Εεπαγ / R = +1,5 A
q = - 2,5 A (10s - 0) + 1,5 A (20s - 10s) = -25 Cb + 15 Cb = -10 Cb
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Λεπτή ομογενής ράβδος ΑΓ μήκους ℓ είναι αρθρωμένη με το ένα άκρο της Α σε οριζόντιο επίπεδο και σχηματίζει γωνία κλίσης φ=45° με αυτό. H μάζα της ράβδου είναι Μ=10kg. Η ράβδος στηρίζεται με το άλλο άκρο της Γ σε λείο κατακόρυφο τοίχο. Σε σημείο Δ της ράβδου που απέχει από το μέσον Κ απόσταση ΔΚ=ℓ/4 είναι δεμένο αβαρές νήμα το οποίο είναι τυλιγμένο γύρω από τον μικρό δίσκο ακτίνας r σταθερής τροχαλίας. Ο μεγάλος δίσκος της τροχαλίας έχει ακτίνα R, με R=2r και έχει τυλιγμένο άλλο αβαρές νήμα στο άκρο του οποίου είναι συνδεδεμένο σώμα Σ1, μάζας m1 =1kg . Όλο το σύστημα ράβδου , τροχαλίας και σώματος Σ1 είναι ακίνητο.
Α. Να υπολογιστεί το μέτρο της δύναμης F που ασκεί ο κατακόρυφος τοίχος στο άκρο Γ της ράβδου και το μέτρο της δύναμης Ν, που ασκεί η άρθρωση στη ράβδο στο σημείο Α.
Κάτω από το σώμα Σ1 και στην ίδια κατακόρυφο με αυτό υπάρχει κατακόρυφο ελατήριο σταθεράς k=100N/m το οποίο είναι συνδεδεμένο με δύο σώματα. Με το σώμα Σ2 μάζας m2=3kg που είναι συνδεδεμένο στο πάνω άκρο του και το σώμα Σ3, μάζας m3=1kg που είναι συνδεδεμένο στο κάτω άκρο του και στηρίζεται σε οριζόντιο επίπεδο. Το όλο σύστημα αρχικά ισορροπεί και το Σ1 απέχει από το Σ2 απόσταση h= 0,6m. Κόβουμε το νήμα λίγο πάνω από το Σ1 και αυτό πέφτει ελεύθερα και συγκρούεται πλαστικά με το Σ2 τη χρονική στιγμή t=0. Η κρούση θεωρείται ακαριαία. Το συσσωμάτωμα που δημιουργείται κάνει ΑΑΤ, χωρίς το Σ3 να χάνει την επαφή του με το δάπεδο.
Β. Να αποδείξετε ότι το πλάτος των ταλαντώσεων του συσσωματώματος είναι Α=0,2m.
Γ. Να υπολογίσετε το λόγο της μέγιστης τιμής της δυναμικής ενέργειας της ταλάντωσης του συσσωματώματος, U, προς τη μέγιστη τιμή της δυναμικής ενέργειας του ελατηρίου, Uελmax.
Δ. Να γράψετε την εξίσωση της δύναμης που ασκεί το ελατήριο στο συσσωμάτωμα κατά τη διάρκεια της ταλάντωσης, σε σχέση με την απομάκρυνση x του συσσωματώματος από τη θέση ισορροπίας και να κάνετε και τη γραφική παράσταση (Fελ-x).
Ε. Να υπολογίσετε την μέγιστη τιμή της δύναμης που ασκεί το οριζόντιο επίπεδο στο σώμα Σ3 κατά τη διάρκεια της ΑΑΤ.
Ως θετική θεωρείται φορά κατακόρυφα προς τα επάνω. Δίνεται g=10m/s2.
A. ισορροπία Σ1 : T1 = m1 g = 10 N τροχαλία : Στ(Ο) = 0 => T1 2r - T2 r = 0 => T2 = 20 N ράβδος : Στ(Α) = 0 => - Mg 3l/4 συν45° + FΓ l ημ45° = 0 => FΓ = 100 3/4 = 75 Ν οριζόντια αριστερά
FΑ,x = FΓ = 75 N οριζόντια δεξιά - Mg + FA,y = 0 => FA,y = 100 N κατακόρυφο πάνω
FA2 = 752 + 1002 = 252 52 => FA = 125 N
B. ισορροπία Σ2 : m2 g = k Δl => Δl = 30 / 100 = 0,3 m συσπείρωση (-)
h = 0,5 g t2 => 0,6 = 0,5 10 t2 => t = 0,12½ s v1 = g t = 10 0,12½ m/s = 12½ m/s = 2 3½ m/s
m1 v1 = (m1 + m2) u => 2 3½ = 4 u => u = 3½ / 2 m/s
ισορροπία Σ2,1 : m2,1 g = k Δl' => Δl' = 40 / 100 = 0,4 m συσπείρωση (-)
διατήρηση ενέργειας για την ταλάντωση : 0,5 m2,1 u2 + 0,5 k ( Δl' - Δl )2 = 0,5 k A2 =>
=> 4 3/4 + 100 0,01 = 100 A2 => 3 + 1 = 100 A2 => A2 = 0,04 => A = 0,2 m
Γ. U = ½ k A2 = ½ 100 0,04 = 2 J
Uελατ(x) = ½ k (x + Δl')2 = ½ 100 ( x - 0,4 )2 [ -0,2m , +0,2m ]
Uελατ(-0,2m) = 50 (- 0,2 - 0,4)2 = 50 0,36 = 18 J U / Uελατ(-0,2m) = 2 / 18 = 1/9
Δ. Fελατ(x) = - k (x + Δl') = - 100 (x - 0,4) [ -0,2m , +0,2m ]
E. στο Σ3 ασκείται από το ελατήριο δύναμη : F'ελατ(x) = + 100 (x - 0,4) [ -0,2m , +0,2m ]
Ν - m3 g + F'ελατ(x) = 0 => N - 10 + 100 x - 40 = 0 => N = 50 - 100.x [ -0,2m , +0,2m ]
όταν το Σ2,1 βρίσκεται στην ανώτερη θέση ταλάντωσης x = +0,2m το ελατήριο είναι συσπειρωμένο κατά 0,4m - 0,2m = 0,2m η δύναμη ελατηρίου για το Σ2,1 είναι 100 N/m 0,2 m = 20 N προς τα πάνω ενώ για το Σ3 20 N προς τα κάτω N - m3 g + F'ελατ = 0 => N - 10 + (- 20) = 0 => N = 30 N προς τα πάνω
όταν το Σ2,1 βρίσκεται στην κατώτερη θέση ταλάντωσης x = -0,2m το ελατήριο είναι συσπειρωμένο κατά 0,4m + 0,2m = 0,6m η δύναμη ελατηρίου για το Σ2,1 είναι 100 N/m 0,6 m = 60 N προς τα πάνω ενώ για το Σ3 60 N προς τα κάτω N - m3 g + F'ελατ = 0 => N - 10 + (- 60) = 0 => N = 70 N προς τα πάνω
 Το άκρο Α επιταχύνεται με την επίδραση δύναμης με σταθερή επιτάχυνση αΑ. Αν σε χρόνο Δt=t, το κέντρο μάζας του τροχού K μετατοπιστεί κατά ΔxΚ , τότε από την τροχαλία θα έχει ξετυλιχτεί μήκος ℓ. Για τα ΔxK και ℓ ισχύει η σχέση
Το άκρο Α επιταχύνεται με την επίδραση δύναμης με σταθερή επιτάχυνση αΑ. Αν σε χρόνο Δt=t, το κέντρο μάζας του τροχού K μετατοπιστεί κατά ΔxΚ , τότε από την τροχαλία θα έχει ξετυλιχτεί μήκος ℓ. Για τα ΔxK και ℓ ισχύει η σχέση Κάποια χρονική στιγμή κλείνουμε το διακόπτη δ και ασκούμε στον ΚΛ κατάλληλη δύναμη F παράλληλη στις δύο ράγες ώστε να συνεχίσει να κινείται με την ίδια σταθερή ταχύτητα, υ. Σε χρονική διάρκεια Δt
Κάποια χρονική στιγμή κλείνουμε το διακόπτη δ και ασκούμε στον ΚΛ κατάλληλη δύναμη F παράλληλη στις δύο ράγες ώστε να συνεχίσει να κινείται με την ίδια σταθερή ταχύτητα, υ. Σε χρονική διάρκεια Δt

 Δίνονται ότι m
Δίνονται ότι m Tη χρονική στιγμή t=0 κλείνει ο διακόπτης δ. Τη χρονική στιγμή t
Tη χρονική στιγμή t=0 κλείνει ο διακόπτης δ. Τη χρονική στιγμή t
 Όλο το σύστημα βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο, Β. Αρχικά είναι ακίνητη. Ασκούμε στο μέσον
Όλο το σύστημα βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο, Β. Αρχικά είναι ακίνητη. Ασκούμε στο μέσον
 Παρατηρήθηκε ότι όταν η τάση ήταν
Παρατηρήθηκε ότι όταν η τάση ήταν  Η ένταση του επαγωγικού ρεύματος που διαρρέει τον αγωγό έχει τιμή:
Η ένταση του επαγωγικού ρεύματος που διαρρέει τον αγωγό έχει τιμή: Η μπάλα ανεβαίνει χωρίς τριβές στο όχημα ολισθαίνοντας και φτάνει σε μέγιστο ύψος h χωρίς να χάσει την επαφή του με αυτό. Την ίδια στιγμή το όχημα έχει αποκτήσει ταχύτητα, V πάνω στο λείο οριζόντιο επίπεδο.
Η μπάλα ανεβαίνει χωρίς τριβές στο όχημα ολισθαίνοντας και φτάνει σε μέγιστο ύψος h χωρίς να χάσει την επαφή του με αυτό. Την ίδια στιγμή το όχημα έχει αποκτήσει ταχύτητα, V πάνω στο λείο οριζόντιο επίπεδο. Μεταφέρουμε την χρονική στιγμή t=0 τον μεταγωγό στη θέση
Μεταφέρουμε την χρονική στιγμή t=0 τον μεταγωγό στη θέση  Τη στιγμή της σύγκρουσης των δύο σφαιρών η δύναμη που ασκεί η μία στην άλλη είναι κάθετη στην επιφάνεια επαφής τους. Η κρούση θεωρείται ελαστική. Μετά την κρούση τα κέντρα μάζας των σφαιρών Α και Β έχουν ταχύτητες με μέτρα V
Τη στιγμή της σύγκρουσης των δύο σφαιρών η δύναμη που ασκεί η μία στην άλλη είναι κάθετη στην επιφάνεια επαφής τους. Η κρούση θεωρείται ελαστική. Μετά την κρούση τα κέντρα μάζας των σφαιρών Α και Β έχουν ταχύτητες με μέτρα V Το κλειστό κύκλωμα του πηνίου παρουσιάζει συνολική ωμική αντίσταση R=10Ω. Αφού σχεδιάσετε τη γραφική παράσταση μεταβολής της έντασης του επαγωγικού ρεύματος σε σχέση με το χρόνο υπολογίστε το φορτίο που μετατοπίζεται μέσα στο κύκλωμα από 0 έως 20s. Αυτό είναι
Το κλειστό κύκλωμα του πηνίου παρουσιάζει συνολική ωμική αντίσταση R=10Ω. Αφού σχεδιάσετε τη γραφική παράσταση μεταβολής της έντασης του επαγωγικού ρεύματος σε σχέση με το χρόνο υπολογίστε το φορτίο που μετατοπίζεται μέσα στο κύκλωμα από 0 έως 20s. Αυτό είναι