ΘΕΜΑ

Στην κατακόρυφη διάταξη του σχήματος ο δίσκος ακτίνας R=0,5m περιστρέφεται γύρω από οριζόντιο άξονα χ'χ που διέρχεται από το κέντρο του Κ  και είναι κάθετος στο επίπεδό του. Στοιχειώδης μάζα Δm του δίσκου που βρίσκεται στο σημείο Δ έχει κινητική ενέργεια π^.10^-5J , στροφορμή μέτρου 4^.10^-6 kg m²/s. Η ράβδος μάζας m=0,1kg  μήκους d=1m στο κάτω άκρο του ιδανικού ελατηρίου σταθεράς k=100N/m ταλαντώνεται εξ' αιτίας της περιστροφής του δίσκου.  Η επίπεδη τροχαλία έχει μηδαμινή μάζα, ακτίνα r=0,3m.  Το νήμα μπορεί να ολισθαίνει στην περιφέρεια της τροχαλίας χωρίς τριβές.  Στον χώρο υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο εντάσεως  Β = 0,01 Τ.

Γ1.  Aν διπλασιασθεί η συχνότητα περιστροφής του δίσκου το πλάτος ταλάντωσης της ράβδου 

     (α)  θα αυξηθεί        (β)  θα μειωθεί        (γ)  θα μείνει το ίδιο     μονάδες 2

        Δικαιολογήστε την άποψή σας.     μονάδες 8

Στα άκρα Α, Γ της ράβδου υπάρχουν ακίδες έτσι ώστε καθώς αυτή ταλαντώνεται, ακουμπούν στα σημεία  Α' , Γ'  αντίστοιχα της επιφάνειας υγρού με συνέπεια να δημιουργούνται εγκάρσια κύματα στην επιφάνεια του υγρού με πλάτος Α=2cm.  Η ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού είναι υ=1m/s.  Έστω σημείο Σ της επιφάνειας του υγρού το οποίο απέχει απόσταση  r₁=0,5m   r₂=0,9m  από τα σημεία Α' , Γ'.  

Γ2.  Πόσα σημεία της ευθείας που ορίζεται από τα σημεία Α', Γ' ταλαντώνονται με μέγιστο πλάτος; μονάδες 10

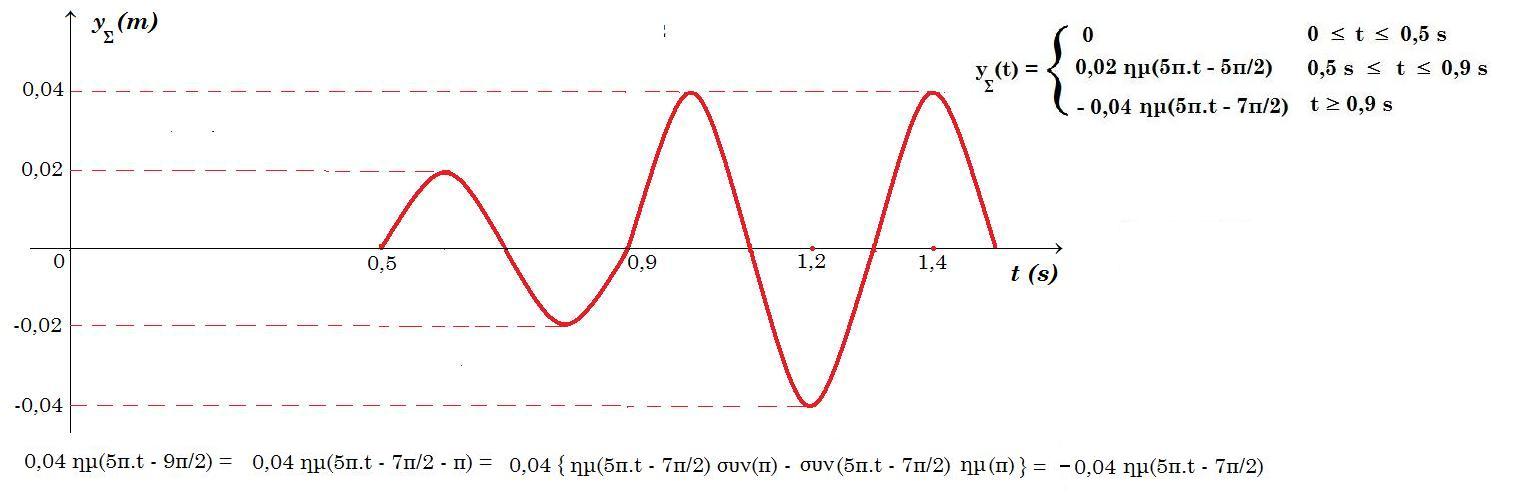
Γ3.  Σχεδιάστε τη γραφική παράσταση της απομάκρυνσης του σημείου Σ συναρτήσει του χρόνου. μονάδες 10

Γ4.  Αν το πλάτος της ταλάντωσης της ράβδου είναι Α=2cm   εκφράστε την τάση στα άκρα της ράβδου συναρτήσει του χρόνου. μονάδες 10

  θέση ισορροπίας ράβδου :  m g = k Δl  =>  0,1 10 = 100 Δl  =>  Δl = 0,01 m = 1 cm     

  x = 0,02 ημ(5πt + θ)         υ = 0,1π συν(5πt + θ)      

  Ε_επαγ = B v d = 0,01 T   0,1π συν(5πt + θ)  1 m  =  π/1000 συν(5πt + θ)     (Volt)     

Η ράβδος κατά την ταλάντωσή της παραμένει σε οριζόντια θέση χωρίς να στρέφεται, κινείται στο κατακόρυφο επίπιδο της τροχαλίας και του δίσκου,  κινείται συνεχώς κάθετα στις δυναμικές γραμμές του μαγνητικού πεδίου.

                                      ΛΥΣΗ

Γ1.

 Κ = ½ Δm  υ²         L = Δm  v (KB) 

K / L =  v / 2(KΔ)  =>  π 10^-5 / 4 10^-6  =  ω_δ / 2  => ω_δ = 5.π rad/s      T = 2π / ω_δ = 2π / 5π = 0,4 s

    ω_δ = v / (KΔ)   συχνότητα διεγέρτη ( του δίσκου που περιστρέφεται )

αμείωτη απλή αρμονική ταλάντωση  ω₀² = k/m = 100 / 0,1 => ω₀² = 1000 => ω₀ = 10√10 = 10.π rad/s 

για να έχουμε μέγιστο πλάτος ταλάντωσης του Σ  ( συντονισμός )  πρέπει  ω_δ = ω₀   

αν διπασιασθεί η συχνότητα του διεγέρτη  ( δίσκου )   2.ω_δ = 2 . 5.π = 10.π = ω₀   το πλάτος ταλάντωσης της ράβδου θα αυξηθεί  θα γίνει μέγιστο ( συντονισμός ) 

Γ2.

υ = λ / Τ  => λ = υ T =  1 m/s  0,4 s  => λ = 0,4 m 

r₂ - r₁ = Ν λ  = N  0,4m      ταλάντωση με μέγιστο πλάτος

    r₁ + r₂ = Α'Γ' = 1 m =>  2 r₂  =  Ν 0,4  + 1 =>  r₂ =  0,2 Ν + 0,5  

 πρέπει   0 £  r₂ £  1 m  =>   0 £   0,2 Ν + 0,5  £  1 m  => 

  =>  - 0,5 £   0,2 Ν  £  0,5  =>  - 2,5 £  Ν  £  2,5      Ν  =  -2, -1, 0, 1, 2 

Ν = -2   r₂ = - 0,4 + 0,5 = 0,1 m       r₁ = 0,9 m

Ν = -1   r₂ = - 0,2 + 0,5 = 0,3 m       r₁ = 0,7 m

Ν = 0     r₂ =  0,5 m                        r₁ = 0,5 m

Ν = 1    r₂ = + 0,2 + 0,5 = 0,7 m       r₁ = 0,3 m

Ν = 2    r₂ =  0,4 + 0,5 = 0,9 m         r₁ = 0,1 m        

       Α'    0,1    0,2   0,3    0,4    0,5     0,6     0,7    0,8    0,9     Γ'    

r₂ - r₁ = Ν λ + λ/2  = N  0,4m + 0,2m       απόσβεση

    r₁ + r₂ = Α'Γ' = 1 m =>  2 r₂  =  Ν 0,4  + 0,2 + 1 =>  r₂ =  0,2 Ν + 0,6  

 πρέπει   0 £  r₂ £  1 m  =>   0 £   0,2 Ν + 0,6  £  1 m  => 

  =>  - 0,6 £   0,2 Ν  £  0,4  =>  - 3 £  Ν  £  2      Ν  =  -3, -2, -1, 0, 1, 2 

Ν = -3   r₂ = - 0,6 + 0,6 = 0 m         r₁ = 1 m     απορρίπτεται

Ν = -2   r₂ = - 0,4 + 0,6 = 0,2 m       r₁ = 0,8 m

Ν = -1   r₂ = - 0,2 + 0,6 = 0,4 m       r₁ = 0,6 m

Ν = 0     r₂ =  0,6 m                        r₁ = 0,4 m

Ν = 1    r₂ = + 0,2 + 0,6 = 0,8 m       r₁ = 0,2 m

Ν = 2    r₂ =  0,4 + 0,6 = 1 m           r₁ = 0 m     απορρίπτεται

εστω  σημείο Ρ της ευθείας  (Α'Γ')  εκτός του ευθυγράμμου τμήματος Α'Γ' προς το μέρος του Α'  έχουμε :  (ΡΑ') - (ΡΓ') = (Α'Γ') = 1 m =  2 . 0,4 m + 0,2 m = 2.λ + λ/2   άρα το σημείο  Ρ  είναι ακίνητο, σημείο απόσβεσης  

Γ3.

πρώτα φθάνει το κύμα από το σημείο Α' σε χρόνο  t₁ = r₁ / v = 0,5 / 1 = 0,5 s     y_Σ(t) = 0      0 £  t £  0,5 s  

y_Σ = A ημ(2π.t/T - 2π.r₁/λ) = 0,02 ημ(5π.t - 2π.0,5/0,4) => y_Σ(t) = 0,02 ημ(5π.t - 5π/2)    0,5 s £  t £  0,9 s     Τ=0,4 s   

μετά φθάνει το κύμα από το σημείο Γ' σε χρόνο  t₂ = r₂ / v = 0,9 / 1 = 0,9 s   οπότε έχουμε συμβολή των δύο κυμάτων :

y_Σ = A ημ(2π.t/T - 2π.r₁/λ)  + A ημ(2πt/T - 2π.r₂/λ) =  0,02 ημ(5π.t - 2π.0,5/0,4)  +  0,02 ημ(5π.t - 2π.0,9/0,4)  =

   =  0,04  συν[π.(0,9 - 0,5) / 0,4]  ημ[5π.t - π.(0,9 + 0,5) / 0,4]  =  0,04  συνπ  ημ[5π.t - π.1,4 / 0,4] = - 0,04 ημ(5π.t - 7π/2) 

=>  y_Σ(t) = - 0,04 ημ(5π.t - 7π/2)  = - 0,04 συν(5π.t)      t ³  0,9 s         Τ = 0,4 s 

ημ(5π.t - 7π/2) = - συν(5π.t) ημ(7π/2)  =  συν(5π.t)

  y_Σ(t)  =  0,02 ημ(5π.t - 2π.0,5/0,4)  +  0,02 ημ(5π.t - 2π.0,9/0,4)  =  0,02 ημ(5π.t - 2,5.π)  +  0,02 ημ(5π.t - 4,5.π)  

t = 0,9 s   0,02 ημ(5π.t - 2,5.π)  +  0,02 ημ(5π.t - 4,5.π) = 0,02 ημ(5π.0,9 - 2,5.π) + 0,02 ημ(5π.0,9 - 4,5.π)  =

               =  0,02 ημ(4,5.π - 2,5.π)  =  0

t = 1 s      0,02 ημ(5π.t - 2,5.π)  +  0,02 ημ(5π.t - 4,5.π)  =  0,02 ημ(5π - 2,5.π)  +  0,02 ημ(5π - 4,5.π)  =

               =  0,02 ημ(2,5.π) +  0,02 ημ(π/2)  =  0,02 + 0,02 = 0,04 m

t = 1,2 s   0,02 ημ(5π.t - 2,5.π)  +  0,02 ημ(5π.t - 4,5.π)  =  0,02 ημ(5π.1,2 - 2,5.π) + 0,02 ημ(5π.1,2 - 4,5.π) =

    =  0,02 ημ(6π - 2,5.π) +  0,02 ημ(6π - 4,5.π)  =  0,02 ημ(3,5.π) +  0,02 ημ(1,5.π)  =  - 0,02  - 0,02 = - 0,04 m

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~