Α1.   (δ)   m u  +  m (-u)  =  2m v_1,2  =>  v_1,2 = 0           K_1,2 = 0

Α2.   (γ)  το πηνίο γίνεται πηγή , δεν υπάρχει κύκλωμα

Α3.   (γ)  λείο επίπεδο  ολίσθιση όχι κύλιση

A4.   (β)    το  b  αυξάνεται   τότε   το πλάτος  Α  μειώνεται

Α5.    α)  Σ             β)  Λ     ( Λ = b/2m )         γ)  Σ           δ)  Σ               ε)  Λ  

Β1.     λ_max,1 =  3 10^-7 m        f = 10¹⁵ Hz        u = 3 10^-7 m  10¹⁵ Hz  =  3 10⁸ m/s  =  c    

λ_max Τ =  0,029  nm.°K     =>   λ_max,1 Τ₁ =  λ_max,2 Τ₂  =   λ_max,2  2Τ₁  =>  λ_max,1  = 2 λ_max,2   =>  λ_max,2  =  3/2 10^-7 m

        f₂ = c / λ_max,2  =  3 10⁸ m/s  /  3/2 10^-7 m  = 2 10¹⁵ Hz           

                 φ  =  2π ( 2 10¹⁵ t  -  2/3 10⁷ x )    (S.I.)           (ii)     

Β2.     λ₁ = 375 10^-9 m     h c / λ₁ =  1250 eV.nm / 375 nm  =  1250 / 375 eV  =  3,333 eV

   L₁  =  m υ₁ R₁  = m υ₁   m υ₁ / Bq  =>   L₁ =  p₁²  / Bq  =>    p₁²  =  L₁ Bq

   Κ₁ = ½ m υ₁²  =  p₁² / 2m    =>  K₁ = L₁ Bq / 2m                    K₁ =   h c / λ₁  -  φ   (1)

   λ₂ =  λ₁ / 2  = 375/2 10^-9 m     h c / λ₁ =  1250 eV.nm / 375/2 nm  =  2500 / 375 eV  =  6,666 eV

  K₂ = L₂ Bq / 2m                    K₂ =   h c / λ₂  -  φ     

                          L₂ = 5 L₁   =>    K₂ = 5 K₁    

    K₂ =   h c / λ₂  -  φ   =>   5 K₁ =   h c / (λ₁/2)  -  φ   =>     5 K₁ =  2 h c / λ₁  -  φ     (2)

 (2) , (1)  =>   5 ( h c / λ₁  -  φ ) =  2 h c / λ₁  -  φ   =>   5 h c / λ₁  -  5 φ  =  2 h c / λ₁  -  φ

=>   3 h c / λ₁  =  4 φ   =>  φ  =  3/4  1250 / 375 eV  =   2,5 eV      βάριο 

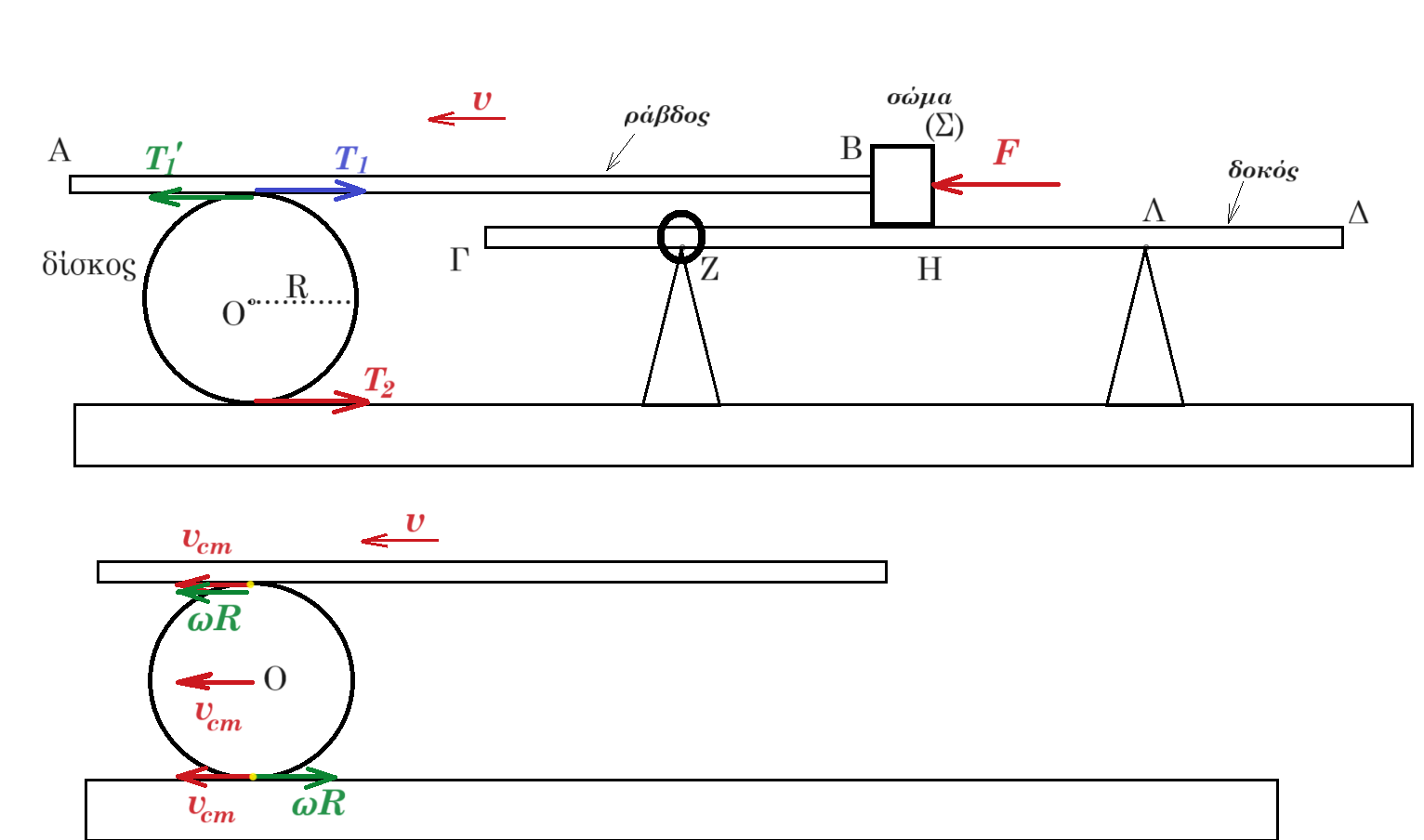
Β3.   Tο σώμα Σ του παρακάτω σχήματος, μάζας m, έχει στερεωθεί στο άκρο Β οριζόντιας, ομογενούς, άκαμπτης και αβαρούς ράβδου ΑΒ. Η ράβδος ακουμπά πάνω στην περιφέρεια ομογενούς δίσκου κέντρου Ο και ακτίνας R.
Ο δίσκος βρίσκεται πάνω σε οριζόντιο δάπεδο με το επίπεδό του κατακόρυφο.
Το σώμα Σ μπορεί να κινείται πάνω σε λεία, οριζόντια, ομογενή και άκαμπτη δοκό ΓΔ μήκους ℓ και μάζας Μ = m / 2.
Η δοκός έχει αρθρωθεί κατάλληλα στο σημείο Ζ, με την κορυφή κατακόρυφου και ακλόνητου υποστηρίγματος (1) που βρίσκεται σε απόσταση ℓ/4 από το άκρο της Γ. Σε απόσταση ℓ/4 από το άκρο Δ της δοκού έχει τοποθετηθεί ένα δεύτερο, όμοιο κατακόρυφο υποστήριγμα (2), πάνω στην κορυφή Λ του οποίου ακουμπά η δοκός ΓΔ. Τα υποστηρίγματα έχουν τοποθετηθεί στο ίδιο οριζόντιο επίπεδο με αυτό στο οποίο βρίσκεται ο δίσκος, όπως φαίνεται στο σχήμα.  Το σύστημα ράβδου-σώματος Σ κινείται προς τα αριστερά με σταθερή ταχύτητα μέτρου υ.  Ο δίσκος εκτελεί κύλιση χωρίς ολίσθηση και η περιφέρειά του βρίσκεται σε συνεχή επαφή με τη ράβδο ΑΒ, χωρίς να παρατηρείται ολίσθηση μεταξύ τους.
Το σώμα Σ, κινούμενο από το Δ προς το Γ, τη χρονική στιγμή t = 0 περνά από το μέσο Η της δοκού. Τη χρονική στιγμή t₁ το σώμα Σ περνά από ένα σημείο της δοκού, στο οποίο η δοκός μόλις που χάνει οριακά την επαφή της με την κορυφή του υποστηρίγματος (2).

  α)   Η απόσταση που έχει διανύσει το σώμα Σ από τη χρονική στιγμή t = 0 μέχρι τη χρονική στιγμή t₁ είναι:

            i.  5l / 6           ii.  3l / 8          iii.  l / 3
Να επιλέξετε τη σωστή απάντηση (μονάδες 2). Να δικαιολογήσετε την επιλογή σας (μονάδες 4)

   β)   Το διάστημα s που έχει διανύσει το κέντρο μάζας Ο του δίσκου από τη χρονική στιγμή t = 0 μέχρι τη χρονική στιγμή t₁ είναι:
            i.  3l / 16           ii.  3l / 8          iii.  l / 16
Να επιλέξετε τη σωστή απάντηση (μονάδα 1). Να δικαιολογήσετε την επιλογή σας (μονάδες 2).
Μονάδες 3
Να θεωρήσετε ότι η αντίσταση του αέρα είναι αμελητέα για όλα τα σώματα

Β3.     Στ_(Ζ) = 0  =>  - Μg l/4  +  mg x  =  0  =>   m/2 g l/4  =  mg x  =>  x = l/8 

 στη θέση  x = l/8  αριστερά από το Ζ  χάνεται η επαφή της ράβδου με το στήριγμα Λ  άρα το σώμα Σ  μετακινείται κατά    l/4  +  l/8  =  3l/8   ( ii )     

η ράβδος και σώμα Σ κινούνται με σταθερή ταχύτητα  υ

στο σώμα ασκείται σταθερή οριζόντια F  προς τα αριστερά οπότε το σύστημα   << σώμα Σ - ράβδος >>  κινείται προς τα αριστερά με σταθερή ταχύτητα λόγω της F 

η ράβδος δέχεται δύναμη τριβής Τ₁  από το άνω σημείο επαφής του δίσκου  =>  T₁ = -  F  είναι αντίθετες  διότι η ράβδος και το σώμα Σ  κινούνται με σταθερή ταχύτητα προς τα αριστερά

ο δίσκος στο ανώτερο σημείο του δέχεται από την ράβδο  δύναμη τριβής Τ₁'  αντίθετη της Τ₁  άρα ίση με την F    και  κυλίεται χωρίς να ολισθαίνει  

μεταξύ δίσκου και οριζοντίου δαπέδου υπάρχει δύναμη τριβής Τ₂   επειδή ο δίσκος κυλίεται χωρίς να ολισθαίνει  το σημείο επαφής του δίσκου με το δάπεδο έχει συνολική ταχύτητα μηδέν   υ_cm = ωR

το ανώτερο σημείο του δίσκου θα έχει συνολική ταχύτητα   υ_cm + ωR =  2υ_cm =  2ωR 

αλλά το ανώτερο σημείο του δίσκου  και  το σύστημα  << ράβδος - σώμα Σ >>  κινούνται με την ίδια ταχύτητα  υ    άρα  υ  =  2υ_cm  =  2ωR  ( ω = υ / 2R  σταθερή )    οπότε διανύουν διαστήματα :   η ράβδος    χ_ράβδ = υ Δt  = 3l/8    και   το κέντρο μάζας του δίσκου   χ_δίσκ =  υ_cm Δt =  υ/2 Δt =  3l/16   ( i )          

επειδή ο δίσκος κινείται με σταθερή ταχύτητα  έχουμε :  ΣF = 0  =>  Τ₁' - Τ₂ = 0   άρα  Τ₂ =  Τ₁' = F  ίσα μέτρα      ακόμη έχουμε :  Στ_(Ο) = F 2R   ροπή ζεύγους δυνάμεων     αλλά   Στ_(Ο) = dL/dt = I α_γων  =>  F 2R  = I α_γων  =>  α_γων =  2R F / I   ( όπου  I = ½ Μ_δίσκου R²  ροπή αδράνειας δίσκου )    δηλαδή ο δίσκος κυλίεται με σταθερή γωνιακή επιτάχυνση  τί γίνεται εδώ !!!          

ΘΕΜΑ  Γ
Εγκάρσιο αρμονικό κύμα, πλάτους Α και μήκους κύματος λ, διαδίδεται χωρίς απώλειες ενέργειας σε ομογενές γραμμικό
ελαστικό μέσο μεγάλου μήκους που ταυτίζεται με τον οριζόντιο ημιάξονα Οx προς τη θετική κατεύθυνση.
Το κύμα παράγεται από πηγή που βρίσκεται στο σημείο Ο στη θέση x = 0 του ελαστικού μέσου και το οποίο αρχίζει να ταλαντώνεται με θετική ταχύτητα τη χρονική στιγμή t = 0 σύμφωνα με την εξίσωση y = A∙ημωt.
Το υλικό σημείο Ο κατά τη διάρκεια της ταλάντωσής του διέρχεται 60 φορές το λεπτό από τη θέση ισορροπίας του.
Κάποια χρονική στιγμή που το υλικό σημείο Ο βρίσκεται στην ακραία αρνητική του απομάκρυνση (y = -A) από την αρχική θέση ισορροπίας του, το υλικό σημείο Δ του ημιάξονα Οx που απέχει από την πηγή Ο οριζόντια απόσταση x_Δ = 2,5 m και έχει ήδη αρχίσει να ταλαντώνεται, βρίσκεται στην ακραία θετική του απομάκρυνση (y = +A) από την αρχική θέση ισορροπίας του. Την ίδια χρονική στιγμή μεταξύ της πηγής (x = 0) και του σημείου Δ υπάρχουν δύο υλικά σημεία που βρίσκονται στην ακραία θετική τους απομάκρυνση (y = +A).
Από τη χρονική στιγμή t = 0 μέχρι τη στιγμή που το κύμα φτάνει στο υλικό σημείο Δ, το συνολικό διάστημα που έχει διανύσει το υλικό σημείο που βρίσκεται στη θέση x = 0 είναι ίσο με 2 m.

Γ1.  Να υπολογίσετε α) την περίοδο Τ (μονάδες 2), β) το μήκος κύματος λ (μονάδες 2) και γ) την ταχύτητα διάδοσης του κύματος (μονάδα 1), καθώς και δ) το πλάτος Α της ταλάντωσης των υλικών σημείων του μέσου (μονάδες 2).
Μονάδες 7
Γ2.  Να αποδείξετε ότι η μαθηματική σχέση που περιγράφει την ταλάντωση του υλικού σημείου Δ είναι: y = A ημ2π(t/Τ - x_Δ/λ).             Μονάδες 5
Γ3.  Να γράψετε την εξίσωση ταχύτητας σε συνάρτηση με το χρόνο για το υλικό σημείο Δ (μονάδες 3) και να σχεδιάσετε τη γραφική της παράσταση σε βαθμολογημένους άξονες, από την χρονική στιγμή t = 0 μέχρι τη χρονική στιγμή t = 8 s (μονάδες 4).           Μονάδες 7
Μειώνουμε τη συχνότητα ταλάντωσης της πηγής, διατηρώντας το ίδιο πλάτος, έτσι ώστε η πηγή Ο και το υλικό σημείο Δ να είναι δύο διαδοχικά σημεία του ελαστικού μέσου, τα οποία κάθε χρονική στιγμή απέχουν το ίδιο από τη θέση ισορροπίας τους και κινούνται με την ίδια ταχύτητα.
Γ4.  Να υπολογίσετε τη μείωση της συχνότητας της πηγής.           Μονάδες 6

  σε  1 λεπτό = 60 δευτερόλεπτα  το σημείο Ο  διέρχεται  60  φορές  από τη θέση ισορροπίας του

  σε μια περίοδο Τ                                                  >>        2  φορές                   >>                  άρα  Τ = 2 sec        f = 0,5 Hz 

  ω = 2π /  2  = π rad/s             η απόσταση ΟΔ είναι  2,5 μήκη κύματος  που ισούται με  2,5 m  άρα  λ = 1 m    

  η ταχύτητα διαδόσεως του κύματος είναι  v_δ = λ f  = 1 m  0,5 Hz =>  v_δ = 0,5 m/s        

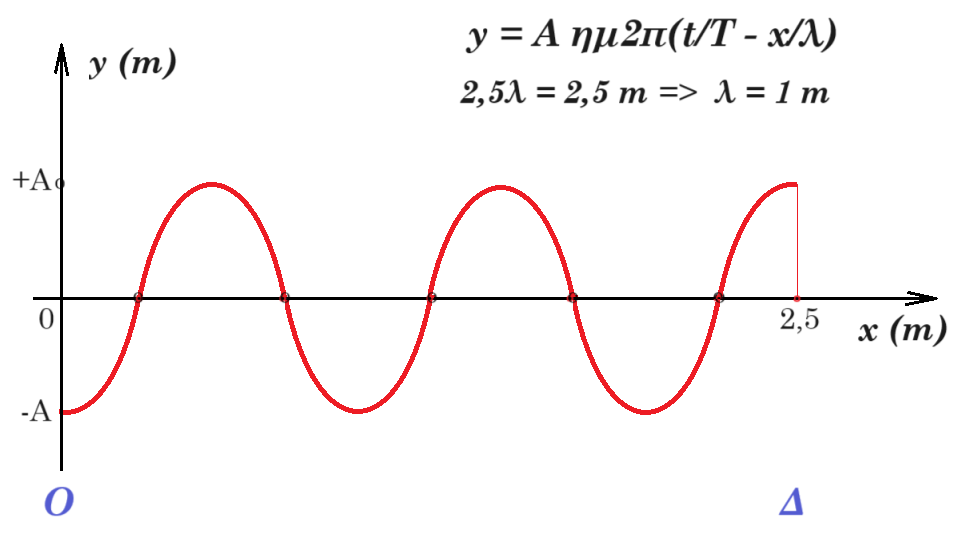
Από τη χρονική στιγμή t = 0 μέχρι τη στιγμή που το κύμα φτάνει στο υλικό σημείο Δ, το συνολικό διάστημα που έχει διανύσει το υλικό σημείο που βρίσκεται στη θέση x = 0 είναι ίσο με 2 m.  ο χρόνος που πέρασε είναι  t_Δ = 2T + T/2 = 5T/2  =  5/2  2 sec  =  5 sec   σε χρόνο μιας περιόδου Τ = 2 sec  το σημείο Ο  διανύει απόσταση  4Α   άρα  σε χρόνο  5Τ/2   διανύει  απόσταση  5/2 4Α = 10 Α = 2 m  =>   A = 0,2 m  πλάτος ταλάντωσης του σημείου Ο  αλλά και του σημείου Δ  

 η εξίσωση του κύματος είναι :  y = A ημ2π(t/T - x/λ)  = 0,2 ημ2π(t/2 - x/1)  =>  y =  0,2 ημ(πt - 2πx)       

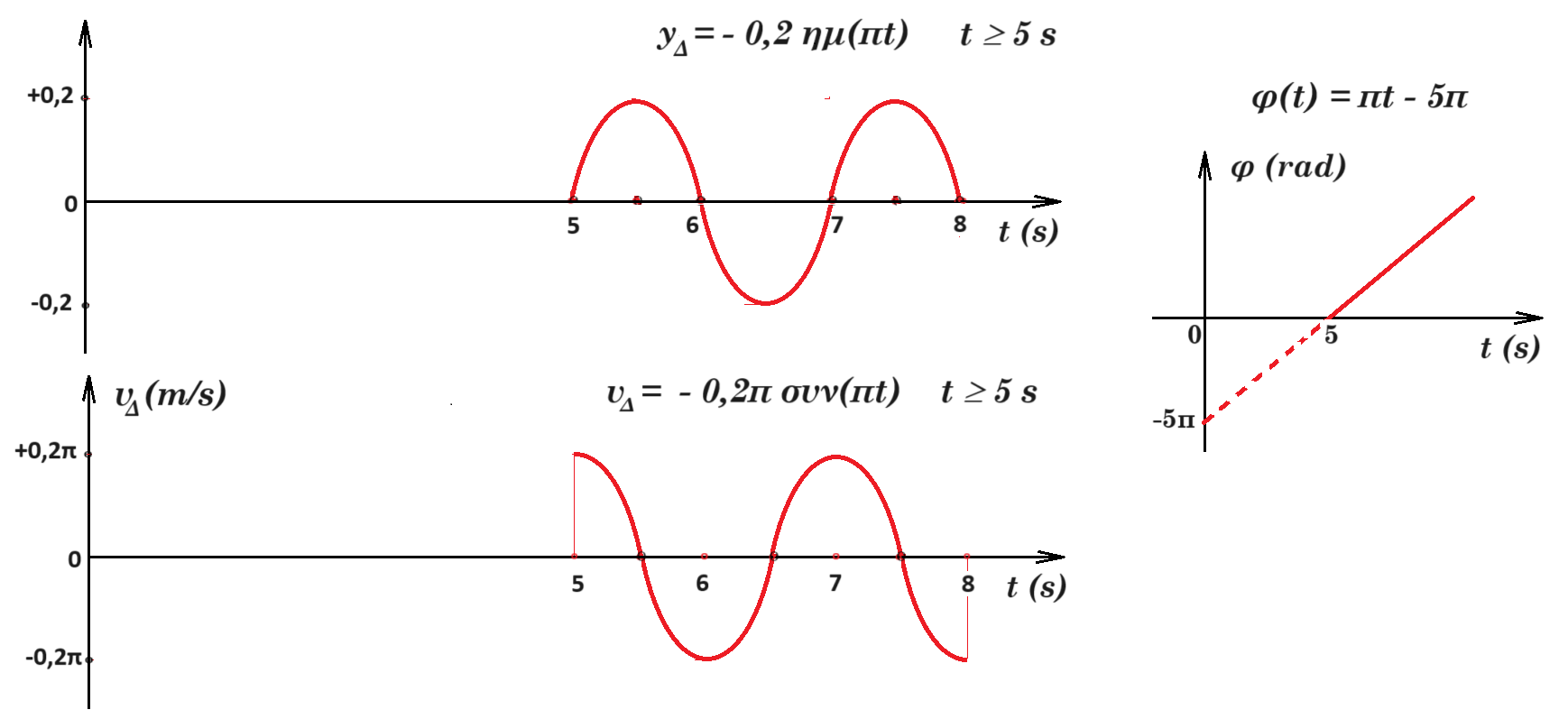
  για το σημείο Δ :  y_Δ =  0,2 ημ(πt - 2π 2,5)  =  0,2 ημ(πt - 5π)  =>  y_Δ = - 0,2 ημ(πt)                

  η εξίσωση της ταχύτητας των σημείων του μέσου είναι :   v  =  0,2π συν(πt - 2πx)   

  για το σημείο Δ :   v_Δ =  0,2π συν(πt - 2π 2,5)  =  0,2π συν(πt - 5π)  =>   v_Δ =  - 0,2π συν(πt) ,   t ³ 5 s       

  για το σημείο Δ :   x_Δ = λ' =>  λ' = 2,5 m        v_δ = λ' f '  =>  0,5 m/s  =  2,5 m  f '  =>  f ' = 0,2 Hz     

          Δf =  f ' - f =  0,2 Hz  -  0,5 Hz  =  - 0,3 Hz    μείωση συχνότητας          

 η εξίσωση της φάσης για το σημείο Α :   φ_(Α) = πt - 5π        

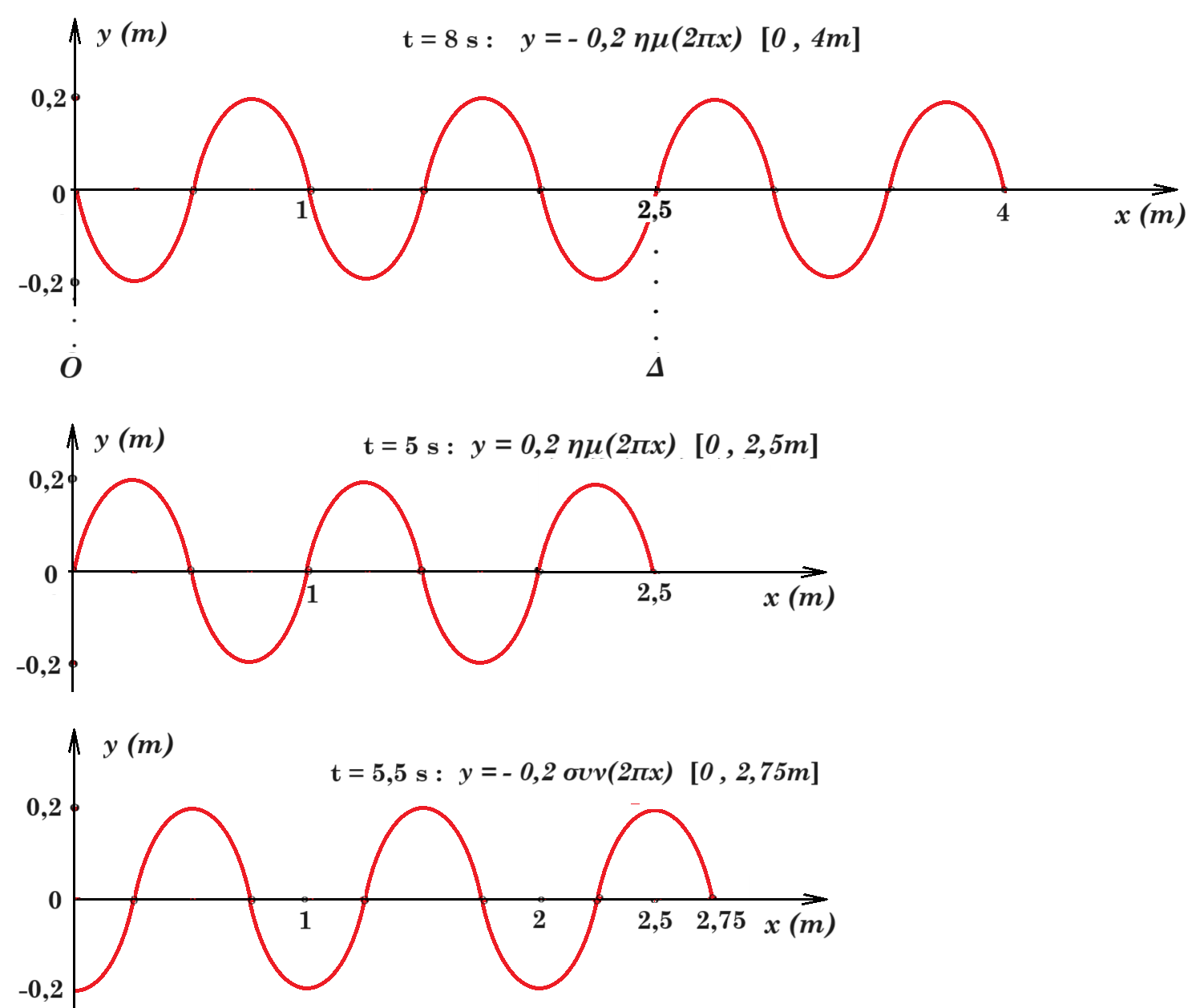
το στιγμιότυπο του κύματος τη στιγμή t = 8 s :  y =  0,2 ημ(πt - 2πx) = 0,2 ημ(8π - 2πx)  =>  y = - 0,2 ημ(2πx)  [0 , 4m]   

το στιγμιότυπο του κύματος τη στιγμή t = 5 s :  y =  0,2 ημ(πt - 2πx) = 0,2 ημ(5π - 2πx)  =>  y = 0,2 ημ(2πx)  [0 , 2,5m] 

το στιγμιότυπο του κύματος τη στιγμή t = 5,5 s :  y =  0,2 ημ(πt - 2πx) = 0,2 ημ(5,5π - 2πx)  =>  y = - 0,2 συν(2πx)  [0 , 2,75m] 

ΘΕΜΑ  Δ
Ένα σώμα Σ μικρών διαστάσεων, μάζας m = 0,4 kg και μια ευθύγραμμη λεπτή και ομογενής μεταλλική ράβδος ΛΜ μήκους L = 1 m και μάζας Μ_ρ = 1,2 kg αμελητέας ωμικής αντίστασης, έχουν τοποθετηθεί πάνω σε λείο οριζόντιο δάπεδο. Το σώμα Σ έχει δεθεί στο ελεύθερο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k = 10 Ν/m, το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο. Το ελατήριο βρίσκεται στο φυσικό του μήκος. Στη θέση αυτή (θέση (2)), το σώμα Σ βρίσκεται σε επαφή με τη ράβδο στο μέσον της Ρ.
Ο άξονας του ελατηρίου, το σώμα Σ και το μέσον της ράβδου βρίσκονται στην ίδια οριζόντια διεύθυνση, η οποία είναι κάθετη στη ράβδο.
Η ράβδος είναι κάθετα τοποθετημένη με τα άκρα της Λ, Μ πάνω σε δύο οριζόντιους και παράλληλους αγωγούς (xΑ) και (yΓ), αμελητέας ωμικής αντίστασης, οι οποίοι έχουν στερεωθεί πάνω στο οριζόντιο δάπεδο. Η ράβδος μπορεί να ολισθαίνει πάνω στους δύο παράλληλους αγωγούς, χωρίς τριβές, έχοντας τα άκρα της σε συνεχή επαφή με αυτούς.
Μεταξύ των άκρων Α και Γ των παράλληλων αγωγών έχει συνδεθεί ένας λεπτός ημικυκλικός αγωγός (ΑΗΓ) κέντρου Ο και ακτίνας r₁ = L / 2,  κατασκευασμένος από σύρμα σταθερής διατομής και ωμικής αντίστασης R₁ = 10 Ω.
Στα άκρα Α και Γ έχει συνδεθεί επιπλέον ένας λεπτός κυκλικός αγωγός (ΔΝΖΘ) κατασκευασμένος από σύρμα σταθερής διατομής ωμικής αντίστασης R₂ = 10 Ω, μέσω των αγώγιμων συρμάτων ΑΔ και ΓΖ που έχουν αμελητέα ωμική αντίσταση. Στον κυκλικό αγωγό σχηματίζονται δύο ημικύκλια ΔΝΖ και ΔΘΖ. Το κέντρο του κυκλικού αγωγού ταυτίζεται με το κέντρο του ημικυκλικού αγωγού ΑΗΓ, ενώ η ακτίνα του r₂ είναι μικρότερη από την ακτίνα r₁. 

Ο διακόπτης (δ) του αγωγού xΑ είναι αρχικά ανοικτός, όπως φαίνεται στο παραπάνω σχήμα.
Στον χώρο μεταξύ της ράβδου ΛΜ και του αγωγού (ΑΗΓ) υπάρχει κατακόρυφο ομογενές μαγνητικό πεδίο, το οποίο στο σχήμα απεικονίζεται με τη γραμμοσκιασμένη περιοχή. Το μέτρο της έντασής του είναι Β = 1 Τ και οι δυναμικές του γραμμές έχουν διεύθυνση κάθετη στο επίπεδο της σελίδας και φορά από τον αναγνώστη προς τη σελίδα.
Μετακινούμε τη ράβδο ΛΜ μαζί με το σώμα Σ, ώστε το ελατήριο να συσπειρωθεί κατά Δℓ = 0,4 m από το φυσικό του μήκος και να έρθει στη θέση (1). Στη συνέχεια αφήνουμε ελεύθερο το σύστημα του σώματος Σ και της ράβδου.

Δ1.   α)  Να αποδείξετε ότι η ράβδος ΛΜ θα αποχωριστεί από το σώμα Σ στη θέση όπου το ελατήριο θα αποκτήσει το φυσικό του μήκος για πρώτη φορά μετά τη στιγμή που τα αφήσαμε ελεύθερα   (μονάδες 2).
        β)  Να βρείτε το πλάτος της απλής αρμονικής ταλάντωσης που θα εκτελέσει το σώμα Σ, αφού αποχωριστεί από τη ράβδο ΛΜ      (μονάδες 3).            Μονάδες 5
Τη χρονική στιγμή t = 0 η ράβδος ΛΜ αποχωρίζεται από το σώμα Σ και με την ταχύτητα που έχει εισέρχεται αμέσως μέσα στο ομογενές μαγνητικό πεδίο.
Δ2.   Να αιτιολογήσετε την ανάπτυξη ηλεκτρεγερτικής δύναμης (ΗΕΔ) από επαγωγή ανάμεσα στα άκρα Λ, Μ της ράβδου αμέσως μετά τη χρονική στιγμή t = 0 και να σχεδιάσετε την πολικότητά της.          Μονάδες 4
Τη χρονική στιγμή t₁ = 1 s (θέση (3)) ασκείται στο μέσον Ρ της ράβδου σταθερή οριζόντια δύναμη προς τη θετική κατεύθυνση μέτρου F = 3 N, κάθετη σε αυτήν. Τη χρονική στιγμή t₂ = 3 s ο διακόπτης (δ) κλείνει (θέση (4)).
Δ3.   Να υπολογίσετε το μέτρο της επιτάχυνσης της ράβδου ΛΜ για το χρονικό διάστημα Δt = (t₂ - t₁) και το μέτρο της ταχύτητάς της στο τέλος αυτού του χρονικού διαστήματος.              Μονάδες 4
Δ4.   Αμέσως μετά το κλείσιμο του διακόπτη (δ):
α)  να αποδείξετε ότι η ράβδος ΛΜ θα εκτελέσει ευθύγραμμη ομαλή κίνηση (μονάδες 2).
β)  να υπολογίσετε τις εντάσεις των ρευμάτων που διαρρέουν τη ράβδο, τον ημικυκλικό αγωγό και τα δύο τμήματα του κυκλικού αγωγού  (μονάδες 4).             Μονάδες 6
Δ5.   Αφού έχει κλείσει ο διακόπτης (δ) να υπολογίσετε:
α)  την ένταση του μαγνητικού πεδίου που δημιουργεί στο κέντρο του Ο αποκλειστικά ο ημικυκλικός αγωγός, κάνοντας χρήση του νόμου των Biot - Savart  (μονάδες 3).
β)  τη συνολική ένταση του μαγνητικού πεδίου που δημιουργούν αποκλειστικά ο ημικυκλικός και ο κυκλικός αγωγός στο κοινό τους κέντρο Ο  (μονάδες 3).             Μονάδες 6
Να θεωρήσετε ότι:
 Η όλη διάταξη βρίσκεται πάνω σε λείο οριζόντιο δάπεδο μεγάλων διαστάσεων το οποίο είναι ηλεκτρικά μονωμένο.
 Η ράβδος μετά το κλείσιμο του διακόπτη τη χρονική στιγμή t₂ παραμένει συνεχώς μέσα στο μαγνητικό πεδίο, δεν επηρεάζεται η κίνησή της από το μαγνητικό πεδίο που δημιουργούν ο ημικυκλικός και ο κυκλικός αγωγός και δεν έρχεται σε επαφή με αυτούς.
 Η αντίσταση του αέρα είναι αμελητέα για όλα τα σώματα.
 Το σχήμα δεν είναι υπό κλίμακα.

μαζί η ράβδος με το σώμα Σ :

  ω² = k / (m + M)  =  10 / 1,6 =  100 / 16  => ω = 10/4 = 2,5 rad/s      T = 2π/ω = 2π/2,5 = 0,8π s

   x = 0,4 ημ(2,5.t + 3π/2)         v = 0,4 2,5  συν(2,5.t + 3π/2) =>  v = 1 συν(2,5.t + 3π/2)        

    α =  - 2,5 ημ(2,5.t + 3π/2)       0  £  t  £  T/4 = 0,2π s

μετά τον αποχώρηση της ράβδου :

  (ω')² = k / m  =  10 / 0,4 =  100 / 4  => ω' = 10/2 = 5 rad/s     

  v_max = ω Α = ω' Α' =>  2,5 rad/s  0,4 m  =  5 rad/s  A'  =>  A' = 0,2 m  

   x = 0,2 ημ(5.t)         v = 0,2 5  συν(5.t) =>  v = 1 συν(5.t)             α =  - 5 ημ(5.t)     αρχίζει να μετράει ο χρόνος από τη στιγμή του αποχωρισμού 

      cos2a  =  cos²a  -  sin²a  =  1  -  2 sin²a  =  2 cos²a  -  1          

Κ = ½ m v²  =  ½  0,4  1² συν²(5.t)  =>  K =  0,2 συν²(5.t)  =  0,1  +  0,1 συν(10.t)  

U = ½ k x²  =  ½  10  0,2² ημ²(5.t)  =>  U =  0,2 ημ²(5.t)  =  0,1  -  0,1 συν(10.t) 

 dK/dt =  m v a  =  0,4  1 συν(5.t)   { - 5 ημ(5.t) }  =  - 2 ημ(5.t) συν(5.t)  =  - ημ(10.t)  

 dU/dt =  k x v  =  10  0,2 ημ(5.t)  1 συν(5.t)  =  2 ημ(5.t) συν(5.t)  = + ημ(10.t)   

[0 , 1s]         v = v_max = 1 m/s           V_ΛΜ = B l v =  1 T  1 m  1 m/s  = 1 Volt

[1s , 3s]       a = F / m = 3 N / 1,2 kg = 2,5 m/s²    

               v = v₀ + a (t - 1) =  1 m/s  + 2,5 m/s² (t - 1s) = 1 + 2,5 (t - 1)    

              V_ΛΜ = B l v =  1 T  1 m  { 1 + 2,5 (t - 1) }  = 1 + 2,5 (t - 1)   (Volt) 

          τη στιγμή   t = 3s        v = 1 + 2,5 (3 - 1)  =  6 m/s      οπότε   V_ΛΜ = 6 Volt

[3s , t]       1/R_ολ  =  1/R₁  +  1 / (R₂/2)  +  1 / (R₂/2)  =  1/10  +  1/5  +  1/5 = 5/10 = 1/2  =>  R_ολ = 2 Ω

             ΣF = F - F_LAPL =  F - B l i =  3  -  1 1 3  =  0  =>  ΣF = 0   =>  a = 0  η ράβδος κινείται με σταθερή ταχύτητα   6 m/s  

             οπότε    V_ΛΜ = B l v =  1 T  1 m  6 m/s  =  6 Volt    

                  i_ολ = B l v / R_ολ = 1 1 6 / 2 = 3 A    

  το φορτίο που διέρχεται από μια διατομή της ράβδου ΛΜ  συναρτήσει του χρόνου :   i = dq/dt  =>  3 A = di/dt  =>  di = 3 dt  =>  i = 3A (t - 3s)           i = 3 (t - 3)     

   τη στιγμή  t = 6s     i = 3A (6s - 3s) = 9 Coulomb