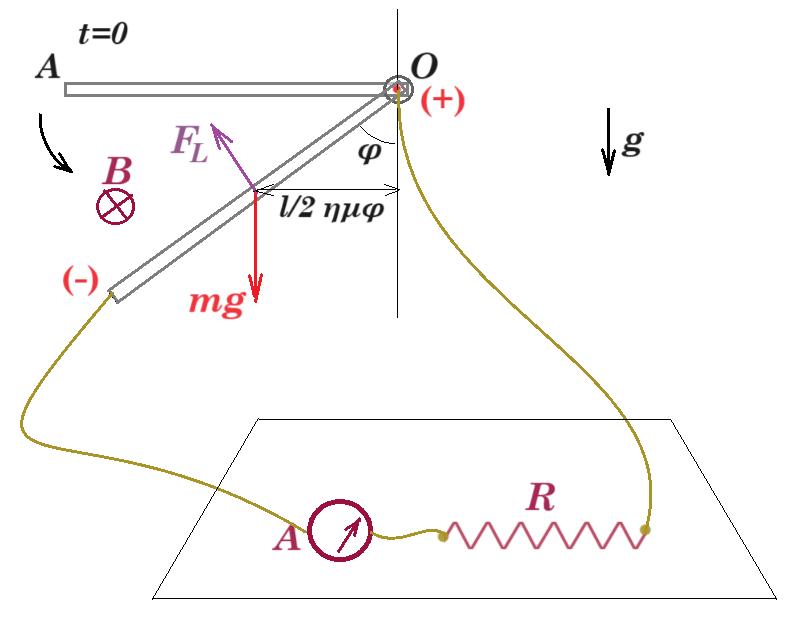
 τη στιγμή μηδέν αφήνεται η ράβδος μάζας m, μήκους l, ωμικής αντίστασης r, από την οριζόντια θέση, ελεύθερη να περιστραφεί
τη στιγμή μηδέν αφήνεται η ράβδος μάζας m, μήκους l, ωμικής αντίστασης r, από την οριζόντια θέση, ελεύθερη να περιστραφεί
k1 = m 4π2 f12 k2 = m 4π2 f22 k1 + k2 = m 4π2 f1,22 = m 4π2 f12 + m 4π2 f22
α = 0 => υ = υορ 14,4 = ½ 0,2 υορ2 => υορ = 12 m/s Εεπ = Β l v = 1 1 12 = 12 V i = 12 / 4 = 3 A FL = B l i = 1 1 3 = 3 N τριβή Τ = 5 Ν - 3 Ν = 2 Ν V = i R = 3A 3Ohm = 9 Volt P = V i = 9 3 = 27 Watt
v' = 6 m/s Ε'επ = Β l v' = 1 1 6 = 6 V i = 6 / 4 = 1,5 A FL = B l i = 1 1 1,5 = 1,5 N - 1,5 N - 2 N = 0,2 kg a' => a' = - 17,5 m/s2 dK/dt = m v' a' = 0,2 6 (- 17,5) = - 21 J/s
PR = - 1,52 4 = - 9 Watt - 2N 6m/s = - 12 J/s
 τη στιγμή μηδέν αφήνεται η ράβδος μάζας m, μήκους l, ωμικής αντίστασης r, από την οριζόντια θέση, ελεύθερη να περιστραφεί
τη στιγμή μηδέν αφήνεται η ράβδος μάζας m, μήκους l, ωμικής αντίστασης r, από την οριζόντια θέση, ελεύθερη να περιστραφεί
Εεπαγ = ΔΦ/Δt = B ΔΑ/Δt = Β π l2 / T = B π l2 / 2π/ω = ½ B ω l2 = i (R + r)
FL = B l i = B l B ω l2 / 2(R + r) = B2 l3 ω / 2(R + r)
Στ(Ο) = I(O) αγων => mg l/2 ημφ - FL l/2 = 1/3 m l2 αγων => mg l/2 ημφ - B2l3ω / 2(R + r) l/2 = 1/3 m l2 αγων =>
=> mg 1/2 ημφ - B2l3ω / 2(R + r) 1/2 = 1/3 m l αγων => mg ημφ - B2l3ω / 2(R + r) = 2/3 m l αγων =>
=> 3g/2l ημφ - 3B2l2ω / 4m(R + r) = αγων ω = dφ/dt αγων = dω/dt = d2φ/dt2
=> 3g/2l ημφ - 3B2l2/ 4m(R + r) dφ/dt = d2φ/dt2
ΟΕΦΕ 2024
ΘΕΜΑ Β
Β1. Διαθέτουμε δύο συσκευές μελέτης του φωτοηλεκτρικού φαινομένου. Η πρώτη έχει στην επιφάνεια της καθόδου της επίστρωση από αλκαλιμέταλλο Α και η δεύτερη αντίστοιχα επίστρωση από αλκαλιμέταλλο Β.
Δίνεται ότι fB = 2fA, όπου fA και fB οι συχνότητες κατωφλίου για τα αλκαλιμέταλλα Α και Β αντίστοιχα.
Φωτόνια ορμής μέτρου p προσπίπτουν στην κάθοδο του αλκαλιμετάλλου A οπότε η τάση αποκοπής είναι Vo.
Φωτόνια ορμής μέτρου 2p προσπίπτουν στην κάθοδο του αλκαλιμετάλλου Β οπότε η τάση αποκοπής είναι Vo'.
Η σχέση που συνδέει τις τάσεις αποκοπής Vo και Vo' είναι: α. Vo' = Vo β. Vo' = 2Vo γ. Vo' = Vo/2
hf = K + φ
h c/λ = p c = e V0 + h fΑ => e V0 = h fΑ - p c
h c/λ' = 2p c = e V0' + h fB => e V0' = h fB - 2p c = h 2fA - 2p c = 2 e V0 => V0' = 2V0
Β2. Δύο εγκάρσια αρμονικά κύματα ίδιου πλάτους και ίδιας συχνότητας διαδίδονται ταυτόχρονα με αντίθετες ταχύτητες κατά μήκος ενός γραμμικού ελαστικού μέσου που ταυτίζεται με τον άξονα x'Ox με αποτέλεσμα να δημιουργηθεί στάσιμο κύμα. Στο σημείο Ο του μέσου (x = 0) δημιουργείται κοιλία και το υλικό σημείο που βρίσκεται στο O, τη χρονική στιγμή t=0 διέρχεται από τη θέση ισορροπίας του κινούμενο κατά τη θετική φορά. Το χρονικό διάστημα μεταξύ δύο διαδοχικών μεγιστοποιήσεων της κινητικής ενέργειας του παραπάνω υλικού σημείου είναι ίσο με 0,1 s και τη χρονική στιγμή t = T/12, όπου Τ η περίοδος ταλάντωσής του, η απομάκρυνσή του είναι ίση με y = +0,1 m.
Η απόσταση μεταξύ δύο διαδοχικών δεσμών του παραπάνω στάσιμου κύματος είναι 0,2 m.
Η εξίσωση του στάσιμου κύματος είναι:
α. y = 0,1συν(5πx) ημ(10πt) (S.I.)
β. y = 0,2συν(10πx) ημ(20πt) (S.I.)
γ. y = 0,2συν(5πx) ημ(10πt) (S.I.)
Τ/2 = 0,1 s => T = 0,2 s ω = 2π/Τ = 2π / 0,2 = 10π rad/s
T/12 = 0,2/12 s = 0,1/6 s λ/2 = 0,2 m => λ = 0,4 m 2πx/λ = 2πx/0,4 = 5πx
εξίσωση στασίμου κύματος : y = 2Α συν(2πx/λ) ημ(ωt) => 0,1 = 2Α συν(5π 0) ημ(10π 0,1/6) =>
=> 0,1 = 2Α 1 ημ(π/6) => 0,1 = 2Α 1/2 => 2Α = 0,2 m
το σημείο Ο είναι κοιλία y = 2Α συν(2πx/λ) ημ(ωt) => y = 0,2 συν(5πx) ημ(10πt) (γ)
Β3. Διπλή τροχαλία (Τ) αποτελείται από 2 κολλημένους ομογενείς και ομοαξονικούς κυλίνδρους ακτίνων r και R όπου
R = 2r. Η τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από σταθερό οριζόντιο άξονα που συμπίπτει με τον άξονα συμμετρίας της και περνά από το Ο.
Ομογενής ισοπαχής δίσκος (Δ) μάζας Μ και ακτίνας R' ισορροπεί έχοντας στο άνω άκρο του στερεωμένο οριζόντιο, αβαρές και μη εκτατό νήμα (Α) του οποίου το άλλο άκρο είναι ακλόνητα στερεωμένο στο ψηλότερο σημείο του εσωτερικού κυλίνδρου της τροχαλίας. Ο δίσκος (Δ) έρχεται σε επαφή με το λείο κατακόρυφο τοίχωμα (1) και με το οριζόντιο δάπεδο (2). Ένα δεύτερο αβαρές, κατακόρυφο και μη εκτατό νήμα (Β) είναι περασμένο στην περιφέρεια του εξωτερικού κυλίνδρου της τροχαλίας και στο κάτω του άκρο είναι στερεωμένο σώμα (Σ) μάζας m και αμελητέων διαστάσεων. Όλα τα σώματα του σχήματος ισορροπούν.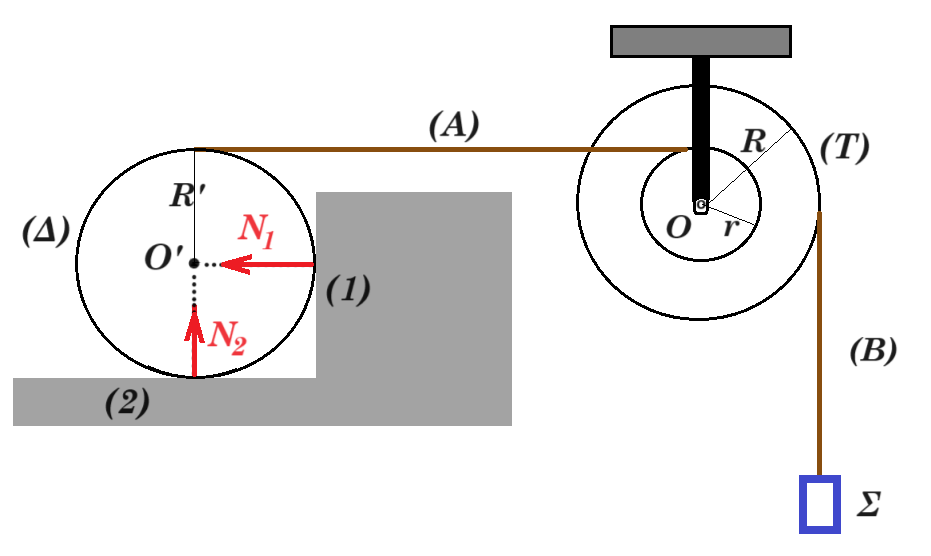
Η διεύθυνση της δύναμης επαφής Ν⃗ 1 που ασκεί το τοίχωμα (1) στον δίσκο (Δ) είναι κάθετη στο τοίχωμα και περνά από το κέντρο του Ο'. Ο λόγος Ν1 / Ν2 των μέτρων της δύναμης Ν⃗ 1 προς το μέτρο της κάθετης δύναμης Ν⃗ 2 που ασκεί το οριζόντιο δάπεδο στο σώμα είναι ίσος με:
α. 4m / M β. 2m / M γ. m / 4M
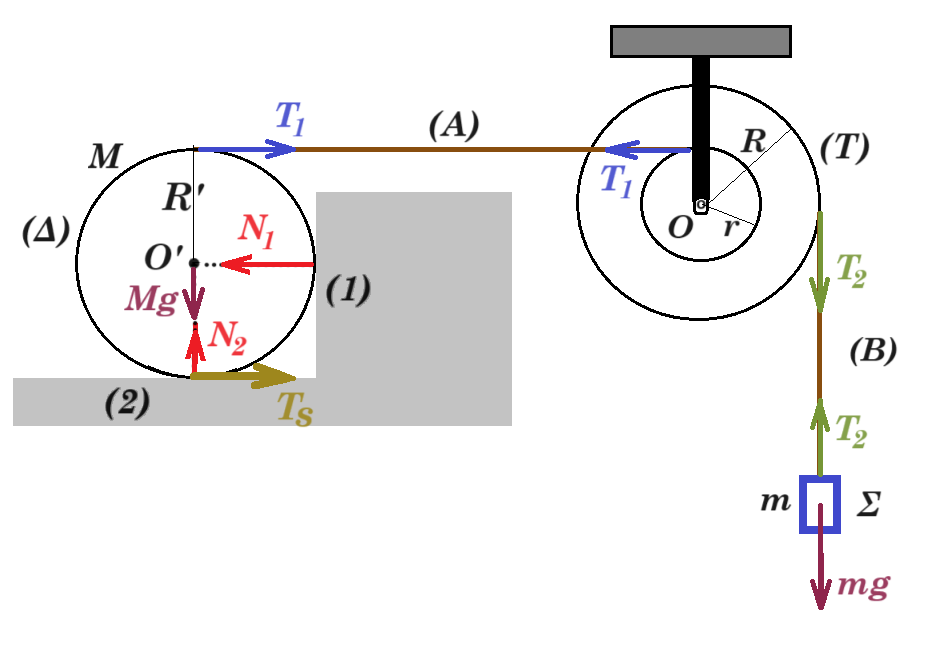
T2 = mg T2 R = T1 r => 2 T2 = T1 Τ1 R' = Ts R' => T1 = Ts
Ts + T1 = N1 => N1 = 2 T1 = 4 T2 = 4 mg Mg = N2
N1 = 4 mg N2 = Mg N1 / N2 = 4m / M
ΟΕΦΕ 2023
ΘΕΜΑ Γ
Οριζόντια ελαστική χορδή μήκους L=0,9m ταυτίζεται με τον άξονα Οx, έχει το ένα άκρο της ακλόνητα στερεωμένο σε σημείο Α (xΑ=+0,9m) ενώ το ελεύθερο άκρο της βρίσκεται στην αρχή Ο (x=0). Το σημείο Ο εκτελεί απλή αρμονική ταλάντωση οπότε δημιουργείται εγκάρσιο αρμονικό κύμα που διαδίδεται προς τη θετική κατεύθυνση του άξονα Οx. Το κύμα ανακλάται στο σημείο Α της χορδής οπότε δημιουργείται ένα δεύτερο εγκάρσιο κύμα που διαδίδεται προς
την αρνητική κατεύθυνση του άξονα Οx. Τα δύο κύματα έχουν ίδιο πλάτος και ίδιο μήκος κύματος, και όταν συμβάλλουν δημιουργείται στη χορδή στάσιμο κύμα με εξίσωση: y=0,4συν(5πx)ημ(4πt) (S.I).
Γ1. Να γράψετε τις εξισώσεις των δύο κυμάτων που δημιουργούν το στάσιμο κύμα. Μονάδες 4
Γ2. Να υπολογίσετε το πλήθος των κοιλιών και των δεσμών που σχηματίζονται στη χορδή. Μονάδες 6
Γ3. Να βρείτε την μέγιστη και την ελάχιστη απόσταση μεταξύ της τρίτης κοιλίας και του τέταρτου δεσμού. Μονάδες 7
Γ4. Τη χρονική στιγμή t1 που η δεύτερη κοιλία βρίσκεται στη θέση που η δυναμική της ενέργεια γίνεται μέγιστη για πρώτη φορά , να βρείτε την επιτάχυνση ταλάντωσης ενός σημείου Μ της χορδής με xΜ=0,25m. Μονάδες 8
Να θεωρήσετε ότι το σημείο Ο (x=0) είναι κοιλία και την t=0 βρίσκεται στη θέση ισορροπίας κινούμενο προς τα θετικά.
ΘΕΜΑ Γ
y=2Aσυν(2πx/λ)ημ(2πt/Τ) (S.I). y=0,4συν(5πx)ημ(4πt) (S.I). A = 0,2 m
2π/λ = 5π => λ = 0,4 m 2π/Τ = 4π => Τ = 0,5 s υ = λ/Τ = 0,4/0,5 = 0,8 m/s
y1 = A ημ(2πt/Τ - 2πx/λ) = 0,2 ημ(4πt - 5πx) y2 = A ημ(2πt/Τ + 2πx/λ) = 0,2 ημ(4πt + 5πx)
0 1 2 3 4 5 6 7 8 9
κ δ κ δ κ δ κ δ κ δ 5 κοιλίες 5 δεσμοί
η τρίτη κοιλία είναι στη θέση x3 = 0,4 m ο τέταρτος δεσμός στη θέση x4 = 0,7 m
ελάχιστη απόσταση = 0,7 - 0,4 = 0,3 m μέγιστη απόσταση = ( 0,32 + 0,42 )½ = 0,5 m
μέγιστη δυναμική ενέργεια συμαίνει ότι το σημείο της κοιλίας είναι σε απομάκρυνση 0,4 m για πρ΄τη φορά δηλαδή t = T/4 = 0,5s / 4 = 1/8 s
y = 0,4 συν(5πx) ημ(4πt) = 0,4 συν(5π 0,25) ημ(4π 1/8) = 0,4 (- √2/2) 1 = - 0,2 √2 m
υ = 1,6π συν(5πx) συν(4πt)
α = - 6,4π2 συν(5πx) ημ(4πt) = - 6,4π2 συν(5π 0,25) ημ(4π 1/8) = - 6,4π2 (- √2/2) 1 = 3,2π2 √2 m/s2
ΟΕΦΕ 2023
ΘΕΜΑ Δ
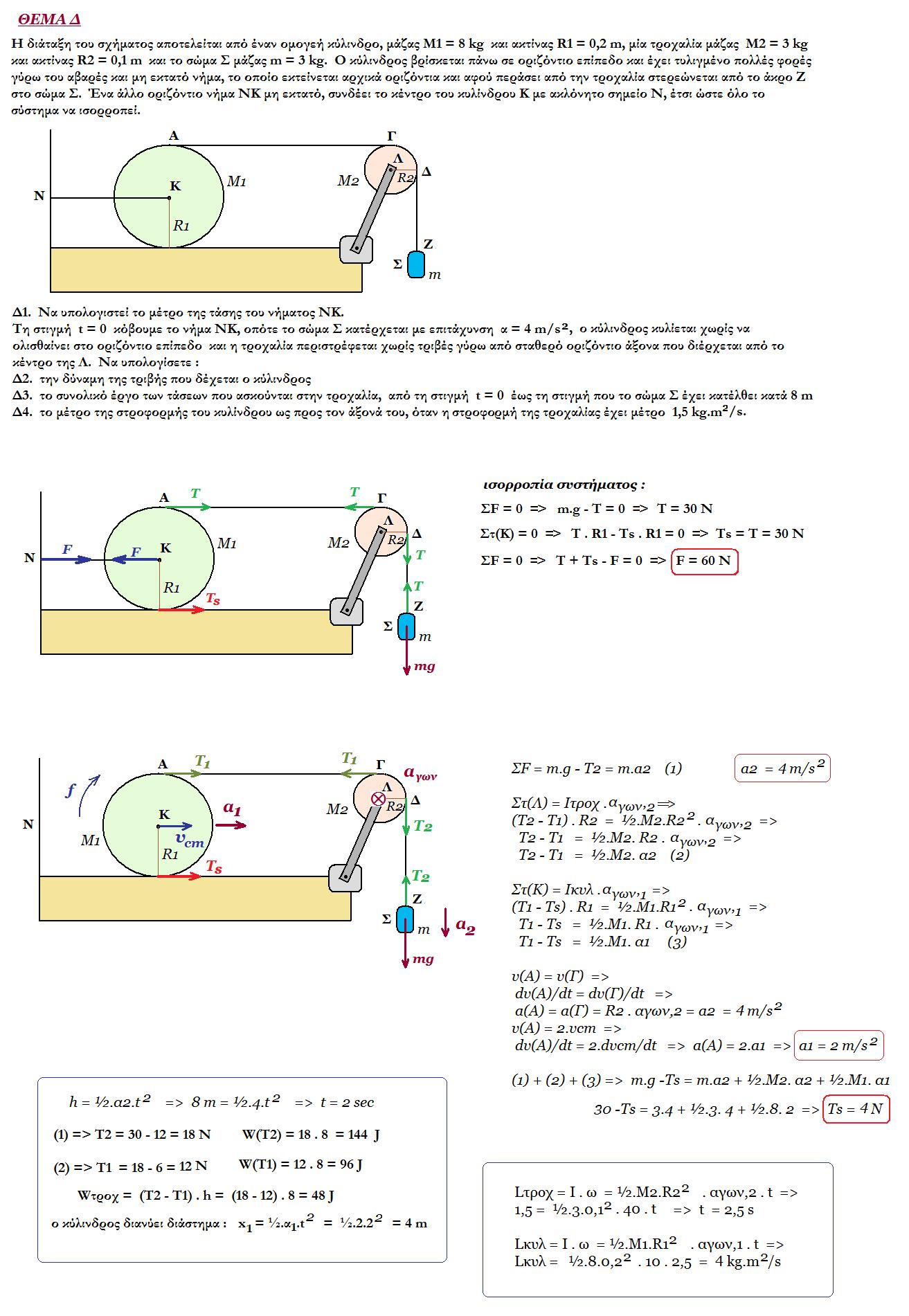
Δύο οριζόντιοι παράλληλοι αγωγοί Αx, Γy μεγάλου μήκους, αμελητέας αντίστασης , που απέχουν μεταξύ τους l = 0.4 m, συνδέονται στα άκρα τους Α και Γ με γεννήτρια Ε = 3 V r = 0,3 Ω. Ο κλάδος ΖΗ του κυκλώματος, παράλληλα συνδεδεμένος με τη γεννήτρια περιέχει ιδανικό πηνίο με n* = 103 σπείρες/m, συντελεστή αυτεπαγωγής L = 0.4 H καθώς και ωμικό αντιστάτη, αντίστασης R1 = 0,6 Ω. Ομογενής ισοπαχής μεταλλική ράβδος ΚΛ μήκους ΚΛ = 0.4 m, ωμικής αντίστασης RΚΛ = 0,3 Ω ηρεμεί οριζόντια, σε διεύθυνση κάθετη στους αγωγούς Αx και Γy έχοντας τα σημεία της Κ και Λ σε επαφή με αυτούς. Η ράβδος βρίσκεται σε χώρο όπου υπάρχει κατακόρυφο ομογενές μαγνητικό πεδίο έντασης Β = 0,1 Τ όπως φαίνεται στο σχήμα. 
Στερεώνουμε τα σημεία Κ και Λ της ράβδου στους αγωγούς Αx και Γy έτσι ώστε να μην μπορεί να κινηθεί και κλείνουμε τον διακόπτη δ.
Δ1. Ι) Υπολογίστε το μέτρο της δύναμης Laplace που ασκείται στην ράβδο αμέσως μετά το κλείσιμο του διακόπτη.
ΙΙ) Όταν το ρεύμα στον κλάδο ΖΗ σταθεροποιηθεί υπολογίστε την ένταση του μαγνητικού πεδίου στο κέντρο του πηνίου. Να κάνετε ένα ποιοτικό διάγραμμα της έντασης του ρεύματος που διαρρέει το πηνίο συναρτήσει του χρόνου από τη στιγμή που κλείνουμε τον διακόπτη και μετά.
Ανοίγουμε τον διακόπτη δ.
Δ2. Τη στιγμή που ο ρυθμός μεταβολής της έντασης του ρεύματος που διαρρέει το πηνίο έχει μέτρο 𝑑𝑖/𝑑𝑡 = 1,5 A/s , υπολογίστε το μέτρο της δύναμης Laplace FL που ασκείται στην ράβδο και σχεδιάστε την.
Δ3. Υπολογίστε το ποσό θερμότητας που θα παραχθεί στη ράβδο από την στιγμή που ανοίξαμε τον διακόπτη μέχρι τη στιγμή που το ρεύμα που διαρρέει το πηνίο θα μηδενιστεί. Να κάνετε ένα ποιοτικό διάγραμμα της έντασης του ρεύματος που διαρρέει το πηνίο συναρτήσει του χρόνου.
Δίνεται η μαγνητική διαπερατότητα του κενού μο = 4π∙10-7 Ν/Α2.
ΘΕΜΑ Δ
όταν κλείνουμε τον διακόπτη
Δ1. i) το πηνίο αντιδρά στην διέλευση ρεύματος οπότε το ρεύμα της πηγής διέρχεται από τη ράβδο ΚΛ η οποία δέχεται δύναμη Laplace i = E / (r + RΚΛ) = 3 V / 0,6 Ω = 5 Α
FL = B l i = 0,1 T 0,4 m 5 A = 0,2 N με κατεύθυνση οριζόντια προς τα δεξιά
ii) οταν σταθεροποιηθούν τα ρεύματα στη διάταξη η ράβδος συνδέεται παράλληλα με τον κλάδο ΖΗ
R1,ΚΛ = 0,6 0,3 / (0,6 + 0,3) = 0,2 Ω Ε = I (r + R1,ΚΛ ) => 3 = I (0,3 + 0,2) => I = 6 A
Vπολική = Ε - Ι r = VZH = VΚΛ => 3V - 6A 0,3Ω = Ιπ R1 = ΙΚΛ RΚΛ => 1,2 V = Ιπ 0,6 Ω = ΙΚΛ 0,3 Ω =>
=> Ιπ = 2 Α ΙΚΛ = 4 Α
από το πηνίο διέρχεται ρεύμα Iπ = 2 Α η ένταση του μαγνητικού πεδίου στο κέντρο του πηνίου είναι Βπ = 4π 10-7 Ν/Α2 2Α 103 σπείρες/m = 8π 10-4 Τ
ανοίγουμε τον διακόπτη
Δ2. η πηγή είναι εκτός κυκλώματος το πηνίο γίνεται πηγή οπότε έχουμε σε σειρά το πηνίο την αντίσταση R1 και τη ράβδο - L di/dt = i (R1 + RΚΛ) => - 0,4 H 1,5 A/s = i 0,9 Ω => i = - 2/3 A
FL = B l i = 0,1 T 0,4 m 2/3 A = 8/300 = 4/150 = 2/75 N με κατεύθυνση οριζόντια προς τα αριστερά
Δ3. στο πηνίο είχε αποθηκευθεί δυναμική ενέργεια UL = 0,5 L i2 = 0,5 0,4 22 = 0,8 J η οποία καταναλώνεται πάνω στις αντιστάσεις Qθερμ. = 0,8 J = QR1 + QΚΛ (1)
QR1 = i2 R1 t QΚΛ = i2 RΚΛ t QR1 / QΚΛ = R1 / RΚΛ = 0,6 Ω / 0,3 Ω = 2 (2)
(1) , (2) => 0,8 J = 2 QΚΛ + QΚΛ => QΚΛ = 0,8/3 = 8/30 = 4/15 J QR1 = 8/15 J
η ράβδος είναι ελεύθερη να κινηθεί κλείνουμε τον διακόπτη
i = iπ + iΚΛ (1) E - L diπ/dt = i r + iπ R1 (2) E - B l v = i r + iΚΛ RΚΛ (3)
FL = B l iΚΛ ΣF = m a => - B l iΚΛ = m dv/dt => iΚΛ = - m/B.l dv/dt (4)
(2) - (3) => - L diπ/dt + B l v = iπ R1 - iΚΛ RΚΛ => - L diπ/dt + B l v = iπ R1 + RΚΛ m/B.l dv/dt =>
=> L diπ/dt + iπ R1 = B l v - RΚΛ m/B.l dv/dt =>
η ράβδος είναι ελεύθερη να κινηθεί ανοίγουμε τον διακόπτη
FL = B l i ΣF = m a => - B l i = m dv/dt => i = - m/B.l dv/dt di/dt = - m/B.l d2v/dt2
- L di/dt + B l v = i (R1 + RΚΛ) => - L.m/B.l d2v/dt2 + B l v = - (R1 + RΚΛ).m/B.l dv/dt =>
=> L.m/B.l d2v/dt2 - (R1 + RΚΛ).m/B.l dv/dt - B l v = 0
Δ = ( (R1 + RΚΛ).m/B.l )2 + 4 L.m/B.l Β.l = ( (R1 + RΚΛ).m/B.l )2 + 4L.m > (R1 + RΚΛ).m/B.l )2
Δ > 0 άρα δύο πραγματικές ρίζες τριωνύμου επίσης √Δ > β
ρ1 = - β/2α + √Δ/2α = +(R1 + RΚΛ).m/B.l / 2L.m/B.l + √Δ/2L.m/B.l =
= + (R1 + RΚΛ)/2L + √Δ/2L.m/B.l > 0 ρ1 > 0
ρ2 = - β/2α - √Δ/2α = +(R1 + RΚΛ).m/B.l / 2L.m/B.l - √Δ/2L.m/B.l =
= + (R1 + RΚΛ)/2L - √Δ/2L.m/B.l < 0 ρ2 < 0
v(t) = V1 e ρ1t + V2 e ρ2t
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
ΟΕΦΕ 2021
Β3. Οι κατακόρυφοι μεταλλικοί αγωγοί Ay και Γy ' έχουν μεγάλο μήκος, αμελητέα ωμική αντίσταση, απέχουν μεταξύ τους σταθερή απόσταση L και η βάση στήριξης τους στο έδαφος είναι ηλεκτρικά μονωμένη. Η λεπτή ομογενής ράβδος ΚΛ μάζας m και μήκους l έχει τα άκρα της Κ και Λ σε ηλεκτρική επαφή με τους αγωγούς Αy, Γy ' και βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο με ένταση μέτρου Β κάθετο στο επίπεδο των αγωγών. Στο κέντρο της ράβδου έχει στερεωθεί το πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k, το άλλο άκρο του οποίου είναι ακλόνητο.
Στην κατάσταση ισορροπίας το ελατήριο είναι συσπειρωμένο κατά Δl.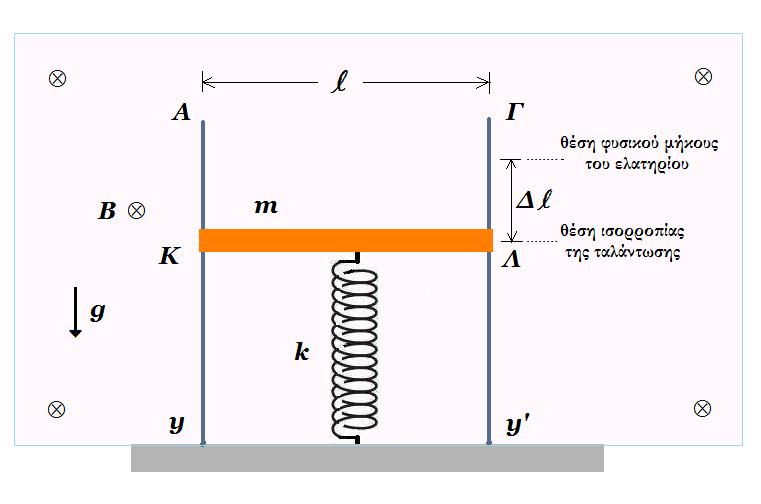
Εκτρέπουμε τη ράβδο από τη θέση ισορροπίας της μέχρι το ελατήριο να αποκτήσει το φυσικό του μήκος και κάποια χρονική στιγμή την αφήνουμε ελεύθερη να εκτελέσει απλή αρμονική
ταλάντωση με σταθερά επαναφοράς D = k. Όταν η απομάκρυνση της ράβδου από τη θέση ισορροπίας της ισούται με Δl∙√3/2, τότε η απόλυτη τιμή της ηλεκτρεγερτικής δύναμης από επαγωγή που αναπτύσσεται στα άκρα της είναι ίση με :
α) B∙g∙l/2 (3m/k)½ β) B∙g∙l/4 (m/k)½ γ) B∙g∙l/2 (m/k)½
ισορροπία ράβδου : mg = kΔl => Δl = mg/k
διατήρηση ενέργειας για την ΑΑΤ :
½ k Δl2 = ½ m v2 + ½ k ( Δl∙√3/2 )2 => k Δl2 = m v2 + k Δl2 ∙3/4 => v2 = kΔl2 /4m = k m2 g2 / 4mk2 => v2 = m g2 / 4k => v = g/2 (m/k)½
επαγωγική τάση : Εεπαγ = B l v = B l g/2 (m/k)½ (γ)
ΟΕΦΕ 2021

ΘΕΜΑ Γ
Τα άκρα Γ και Δ δύο παράλληλων οριζοντίων αγωγών Γx και Δx' αμελητέας αντίστασης, συνδέονται με αγωγό αντίστασης R1 = 0,4 Ω. Επάνω στους δύο αγωγούς είναι τοποθετημένος κάθετα προς τη διεύθυνσή τους ένας άλλος ευθύγραμμος αγωγός ΚΛ μήκους l =1m, o οποίος μπορεί να ολισθαίνει χωρίς τριβές. Η μάζα του αγωγού (ΚΛ) είναι m=0,5kg και η αντίσταση του R2 = 0,1 Ω. Η όλη διάταξη βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο με ένταση μέτρου Β=1Τ, το οποίο είναι κάθετο στο επίπεδο των αγωγών. Ο αγωγός ΚΛ κινείται με σταθερή ταχύτητα μέτρου υ0 = 2 m/ s με τον διακόπτη δ ανοικτό. Τη χρονική στιγμή t0 = 0 κλείνει ο διακόπτης δ χωρίς να δημιουργηθεί σπινθήρας και ασκείται στον αγωγό ΚΛ εξωτερική δύναμη F μεταβλητού μέτρου, της ίδιας κατεύθυνσης με την ταχύτητα του αγωγού, η οποία τον εξαναγκάζει να αποκτήσει σταθερή επιτάχυνση μέτρου α = 1 m/s2. 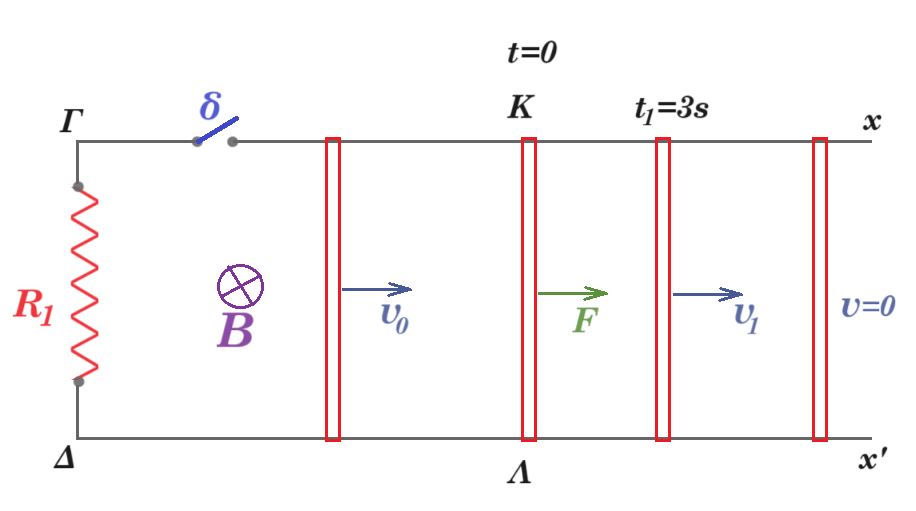
Γ1. Να γράψετε τη χρονική εξίσωση της δύναμης F. Μονάδες 7
Γ2. Να βρείτε το επαγωγικό φορτίο που διέρχεται από μια διατομή του αγωγού ΚΛ από τη χρονική στιγμή 1s έως τη στιγμή 3s. Μονάδες 7
Τη χρονική στιγμή t1 = 3s καταργείται η δύναμη F και ο αγωγός ΚΛ αρχίζει να επιβραδύνεται μέχρι να μηδενιστεί η ταχύτητά του.
Γ3. Να υπολογίσετε το ρυθμό μεταβολής της ορμής του αγωγού τη χρονική στιγμή που η ταχύτητά του ισούται με το μισό της μέγιστης τιμής της μετά την κατάργηση της F . Μονάδες 5
Γ4. Να βρείτε τη θερμότητα που απέβαλλε το κύκλωμα κατά τη διάρκεια της επιβραδυνόμενης κίνησης. Μονάδες 6
Να θεωρήσετε αμελητέες τις αντιστάσεις του αέρα.
Γ1. στα άκρα του αγωγού ΚΛ επάγεται τάση Εεπαγ = B l v0 = 1 1 2 = 2 Volt
τη στιγμή t = 0 που κλείνει ο διακόπτης η ράβδος ΚΛ στα άκρα της έχει τάση οπότε κλείνει κύκλωμα που διαρρέεται από ρεύμα Ι0 = B l v0 / (R1 + R2) = 2 V / 0,5 Ω = 4 Α έτσι δέχεται δύναμη Laplace FL = B l I0 = 1 4 1 = 4 N επειδή στη ράβδο ΚΛ ασκείται δύναμη F αυτή επιταχύνεται αλλάζει η ταχύτητα, ισχύουν : B l v = i (R1 + R2) v = v0 + a t = 2 + 1 t = 2 + t
ΣF = m a => F - FL = m a => F - B l i = m a => F - B2l2v/ (R1 + R2) = m a => F - 1212(2 + t)/ 0,5 = 0,5 1 => F - 2t - 4 = 0,5 => F(t) = 2t + 4,5 (S.I.)
Γ2. i = B l v / (R1 + R2) = 1 1 (2 + t) / 0,5 => i(t) = 4 + 2t i(1) = 6A i(3) = 10A
q = (6A + 10A)(3s - 1s) / 2 = 16 Coulomb
i = dq/dt => dq = i dt = (4 + 2t) dt => q(t) = 4t + t2 q(0) = 0
q(1) = 4 1 + 12 = 5 C q(3) = 4 3 + 32 = 12 + 9 = 21 Coulomb Δq = 21 - 5 = 16 C
Γ3. τη στιγμή t1 = 3s ο αγωγός ΚΛ έχει ταχύτητα v1 = v0 + a t = 2 + 1 3 = 5 m/s τότε καταργείται η F ΣF = m a => - FL = m a => - B l i = m a => - B2l2v/ (R1 + R2) = m a => - 1212v/ 0,5 = 0,5 a => a = - 4v
dv/dt = - 4 v => dv / v = - 4 dt => ln (v / v1 ) = - 4 t => v(t) = 5 e - 4 t a(t) = -20 e - 4 t
η μέγιστη ταχύτητα είναι 5 m/s το μισό 2,5 m/s ΣF = - FL = - B l i = - B2l2v/ (R1 + R2) = - 1212 2,5 / 0,5 = - 5 Ν
Γ4. η κινητική ενέργεια της ράβδου ΚΛ τη στιγμή t1 = 3s μετατρέπεται σε θερμότητα πάνω στις αντιστάσεις
Κ1 = ½ m v12 = ½ 0,5 52 = 25/4 J = Qθερμ
ΟΕΦΕ 2021 Β' φάση
Δύο ίδιες, λεπτές, ισοπαχείς και ομογενείς ράβδοι ΟΑ και ΟΓ, που έχουν μάζα Μ=3kg και μήκος l=1m η κάθε μία, συγκολλούνται στο ένα άκρο τους Ο, ώστε να σχηματίζουν ορθή γωνία. Το σύστημα των δύο ράβδων έχει στο άκρο Α της ράβδου ΟΑ άρθρωση και ισορροπεί με τη βοήθεια αβαρούς και μη εκτατού νήματος, το οποίο σχηματίζει γωνία φ (ημφ=0,8) με τη ράβδο ΟΓ που είναι οριζόντια. Στο άκρο Γ της ράβδου ΟΓ είναι στερεωμένο το ένα άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k=50Ν/m. Στο άλλο άκρο του ελατηρίου έχει δεθεί σώμα Σ μάζας m=0,5kg. Το ένα άκρο του νήματος είναι δεμένο στο σημείο Ζ, το οποίο απέχει οριζόντια απόσταση l/4 από το σημείο συγκόλλησης Ο και το άλλο άκρο του είναι στερεωμένο στην οροφή.
Δ1. Να υπολογίσετε το μέτρο της τάσης του νήματος και τη δύναμη που δέχεται η ράβδος ΟΑ από την άρθρωση Α.
Απομακρύνουμε το σώμα Σ κατά μήκος του άξονα του ελατηρίου προς τα πάνω μέχρι το ελατήριο να συσπειρωθεί κατά Δl=0,1m και τη χρονική στιγμή t=0 τo αφήνουμε ελεύθερο να κινηθεί.
Δ2. Να γράψετε τη χρονική εξίσωση της απομάκρυνσης του σώματος από τη θέση ισορροπίας της ταλάντωσης, της κινητικής ενέργειας του σώματος, της δυναμικής ενέργειας της ταλάντωσης, του ρυθμού μεταβολής της κινητικής ενέργειας, της τάσης του νήματος στο σημείο Ζ. Ποιά είναι η μικρότερη και μεγααλύτερη τιμή της τάσης του νήματος και πότε συμβαίνει αυτό;
Δ3. Να βρείτε για ποιες τιμές του πλάτους της ταλάντωσης του σώματος Σ το νήμα θα παραμείνει τεντωμένο.
Να θεωρήσετε : αμελητέες τις αντιστάσεις του αέρα, ως θετική αντίθετη της φοράς του βάρους.
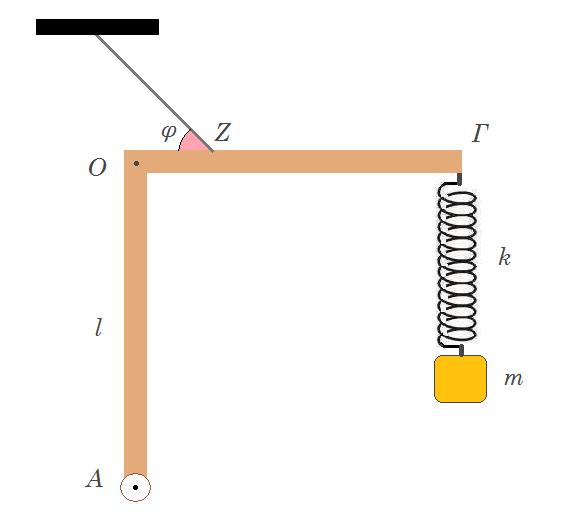
Δ1. θετική κατεύθυνση προς τα πάνω και δεξιά θετική ροπή προς τα έξω
ισορροπία Σ : Fελατ - mg = 0 => mg = Fελατ = k x0 => 0,5 10 = 50 x0 => x0 = 0,1 m επιμήκυνση
ροπές ως προς Ο : Στ(Ο) = 0 => - M g l/2 - Fελατ l + Ty l/4 + Fx,A l = 0 =>
=> - M g l/2 - m g l + Τ ημφ l/4 + Fx,A l = 0 =>
=> 3 10 /2 + 0,5 10 = T 0,8 /4 + Fx,A => T + 5 Fx,A = 100 (1)
ΣFx = 0 => - Tx + Fx,A = 0 => Τ συνφ = Fx,A => 0,6 Τ = Fx,A (2)
(1) , (2) => Τ + 5 0,6 Τ = 100 => 4 Τ = 100 => Τ = 25 Ν (3) άρα Fx,A = 0,6 25 = 15 Ν
ΣFy = 0 => - 2 M g - Fελατ + Ty + Fy,A = 0 => - 2 M g - m g + T 0,8 + Fy,A = 0 =>
=> 2 3 10 + 0,5 10 = 0,8 T + Fy,A => 0,8 T + Fy,A = 65 (4)
(4) (3) => 0,8 25 + Fy,A = 65 => Fy,A = 45 Ν οπότε Fx,A = 15 Ν
FA2 = 152 + 452 = 10 152 => FA = 15√10 Ν

Δ2. το σώμα ήταν στη Θ.Ι. του το ελατήριο επιμηκυμένο κατά 0,1 m και αρχίζει την ταλάντωσή του όταν τοα ελατήριο έχει συσπείρωση 0,1 m άρα το σώμα ξεκινά 0,2 m πάνω από τη Θ.Ι. του οπότε Α = 0,2 m x(0) = +A = +0,2m
ω2 = k / m = 50 / 0,5 = 100 => ω = 10 rad/s T = 2π/ω = π/5 s x(t) = 0,2 ημ(10t + π/2)
υ(t) = 2 συν(10t + π/2) α(t) = - 20 ημ(10t + π/2) ΣF(t) = m a(t) = - 10 ημ(10t + π/2)
K(t) = ½ m v(t)2 = ½ ½ 4 συν2(10t + π/2) = 1 συν2(10t + π/2) = 1 - ημ2(10t + π/2) => K(x) = 1 - 25x2 , -0,2m £ x £ +0,2m
U(t) = ½ k x(t)2 = ½ 50 0,04 ημ2(10t + π/2) = 1 ημ2(10t + π/2) => U(x) = 25x2 , -0,2m £ x £ +0,2m
dK/dt = m v(t) a(t) = 0,5 2 συν(10t + π/2) [ - 20 ημ(10t + π/2) ] =
= - 20 συν(10t + π/2) ημ(10t + π/2) = - 10 ημ(20t + π) = + 10 ημ(20t)
ΣF(t) = m a(t) => - m g + Fελατ = m a(t) => Fελατ(t) = + 5 - 10 ημ(10t + π/2) = 5 - 50 x(t) x(0) = +0,2m Fελατ(0) = 5 - 10 ημ(π/2) = 5 - 10 1 = - 5 Ν προς τα κάτω διότι το ελατήριο αρχικά είναι συσπειρωμένο Δl =0,1 m Fελατ(0) = k Δl = 50 N/m 0,1 m = 5 N προς τα κάτω
FΓ = - Fελατ = - 5 + 10 ημ(10t + π/2) = - 5 + 50 x(t)
ροπές ως προς Α : Στ(Α) = 0 => - M g l/2 + FΓ l + Ty l/4 + Τx l = 0 =>
=> - M g /2 - 5 + 10 ημ(10t + π/2) + T 0,8 /4 + 0,6 Τ = 0 =>
=> - 15 - 5 + 10 ημ(10t + π/2) + T 0,8 /4 + 0,6 Τ = 0 =>
=> 20 - 10 ημ(10t + π/2) = 0,8 Τ => Τ(t) = 25 - 12,5 ημ(10t + π/2) = 25 - 12,5 x / 0,2 = 25 - 62,5 x = T(x)
t = 0 T(0) = 25 - 12,5 ημ(π/2) = 25 - 12,5 = 12,5 Ν
t = T/4 = π/20 s T(π/20) = 25 - 12,5 ημ(10 π/20 + π/2) = 25 - 12,5 ημ(π/2 + π/2) = 25 N
ελάχιστη τιμή της τάσης του νήματος στο σημείο Ζ συμβαίνει όταν :
ημ(10t + π/2) = +1 => 10t + π/2 = 2Νπ + π/2 => t = Νπ/5 Ν = 0, 1, 2, 3, ...
1η φορά : Ν = 0 τότε t = 0 s τότε T(0) = 25 - 12,5 ημ(π/2) = 25 - 12,5 = 12,5 N
2η φορά : Ν = 1 τότε t = π/5 s τότε T(π/5) = 25 - 12,5 ημ(10 π/5 + π/2) = 25 - 12,5 ημ(2π + π/2) = 25 - 12,5 ημ(π/2) = 25 - 12,5 = 12,5 N
μέγιστη τιμή της τάσης του νήματος στο σημείο Ζ συμβαίνει όταν :
ημ(10t + π/2) = - 1 => 10t + π/2 = 2Νπ + 3π/2 => t = Νπ/5 + π/10 Ν = 0, 1, 2, ....
1η φορά μετά την t0 = 0 : Ν = 0 τότε t = π/10 s τότε T(π/10) = 25 - 12,5 ημ(10 π/10 + π/2) = 25 - 12,5 ημ(3π/2) = 25 - 12,5 ημ(3π/2) = 25 + 12,5 = 37,5 N
Δ3.
Τ(t) = 25 - 12,5 ημ(10t + π/2) = 25 - 12,5 x / 0,2 = 25 - 62,5 x = T(x)
- A £ x £ + A 25 - 62,5 A £ Τ £ 25 + 62,5 A
η μικρότερη τιμή της τάσης του νήματος είναι η Τελαχ = 25 - 62,5 Α η οποία συμβαίνει όταν το σώμα βρίσκεται στο άνω άκρο της ταλάντωσής του x = +A οπότε για να είναι το νήμα τεντωμένο πρέπει Τ > 0 => 25 - 62,5 Α > 0 => Α < 25/62,5 = 0,4 m εάν το πλάτος της ταλάντωσης του σώματος είναι μεγαλύτερο από 0,4 m το νήμα χαλαρώνει
FΓ = - Fελατ = - 5 + 50 x(t)
ροπές ως προς Α : Στ(Α) = 0 => - M g l/2 + FΓ l + Ty l/4 + Τx l = 0 =>
=> - 30 / 2 - 5 + 50 x(t) + T 0,8 /4 + 0,6 Τ = 0 => 15 + 5 - 50 x(t) = T 0,8 /4 + 0,6 Τ =>
=> 20 - 50 x(t) = 0,8 T => T = 25 - 62,5 x - A £ x £ + A 25 - 62,5 A £ Τ £ 25 + 62,5 A
ΘΕΜΑ 5.
Οι κατακόρυφοι μεταλλικοί αγωγοί Αy και Γy' έχουν μεγάλο μήκος αμελητέα ωμική αντίσταση και απέχουν απόσταση l = 1 m και η βάση στήριξης τους στο έδαφος είναι ηλεκτρικά μονωμένη. Ο αγωγός ΚΛ μήκους l = 1 m μάζας m = 200 g και ωμικής αντίστασης RΚΛ = 0,4 Ω έχει τα άκρα του Κ και Λ σε ηλεκτρική επαφή με τους αγωγούς Αy και Γy' και απέχει κατακόρυφη απόσταση Η= 6 m από το έδαφος. Η όλη διάταξη βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο έντασης Β = 0,5 Τ κάθετο στο επίπεδο των αγωγών. Τα άκρα Α και Γ συνδέονται με αντιστάτη ωμικής αντίστασης R = 0,1 Ω. Κάποια στιγμή εκτοξεύουμε τον αγωγό ΚΛ με κατακόρυφη ταχύτητ μέτρου υo = 1 m/s με φορά προς τα κάτω. Στην κίνηση του αγωγού αντιτίθεται συνολική δύναμη τριβής μέτρου Τ = 1 Ν λόγω της επαφής με τους κατακόρυφους αγωγούς. Ο αγωγός ΚΛ αφού διανύσει κατακόρυφη απόσταση d = 4 m εξέρχεται του μαγνητικό πεδίο έχοντας αποκτήσει οριακή ταχύτητα.
Δ1. Υπολογίστε την κινητική ενέργεια του αγωγού ΚΛ όταν εξέρχεται από το μαγνητικό πεδίο.
Δ2. Υπολογίστε τον ρυθμό μεταβολής της κινητικής ενέργειας του αγωγού ΚΛ όταν η τάση στα άκρα του είναι 0,15 V.
Δ3. Εκφράστε την επιτάχυνση του αγωγού συναρτήσει της ταχύτητάς του κατά τη διάρκεια της κίνησής του μέσα στο μαγνητικό πεδίο.
Δ4. Βρείτε τον λόγο QR / QT της συνολικής θερμότητας που εκλύεται λόγω φαινομένου Joule στους αντιστάτες προς τη συνολική θερμότητα που εκλύεται λόγω τριβής μέχρι να φθάσει ο αγωγός στο έδαφος.
Καθ'όλη τη διάρκεια της κίνησης ο αγωγός παραμένει οριζόντιος, οι αντιστάσεις του αέρα αμελητέες.
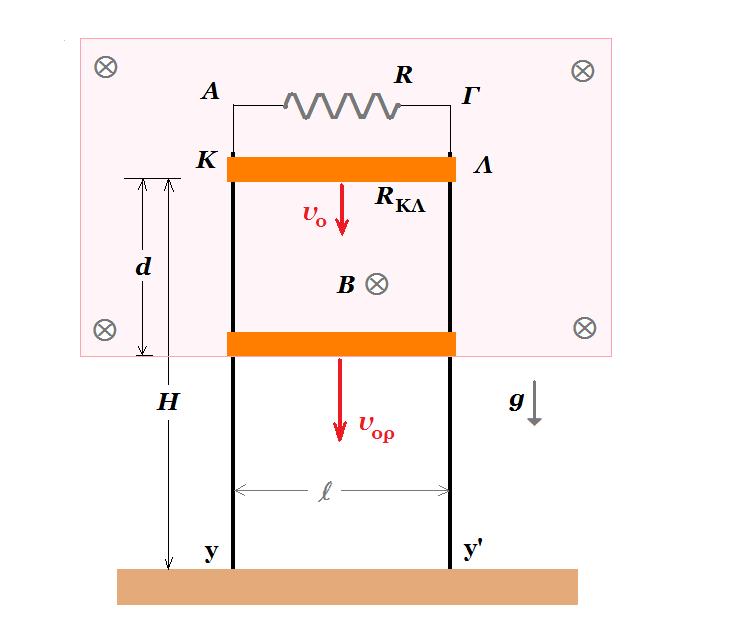
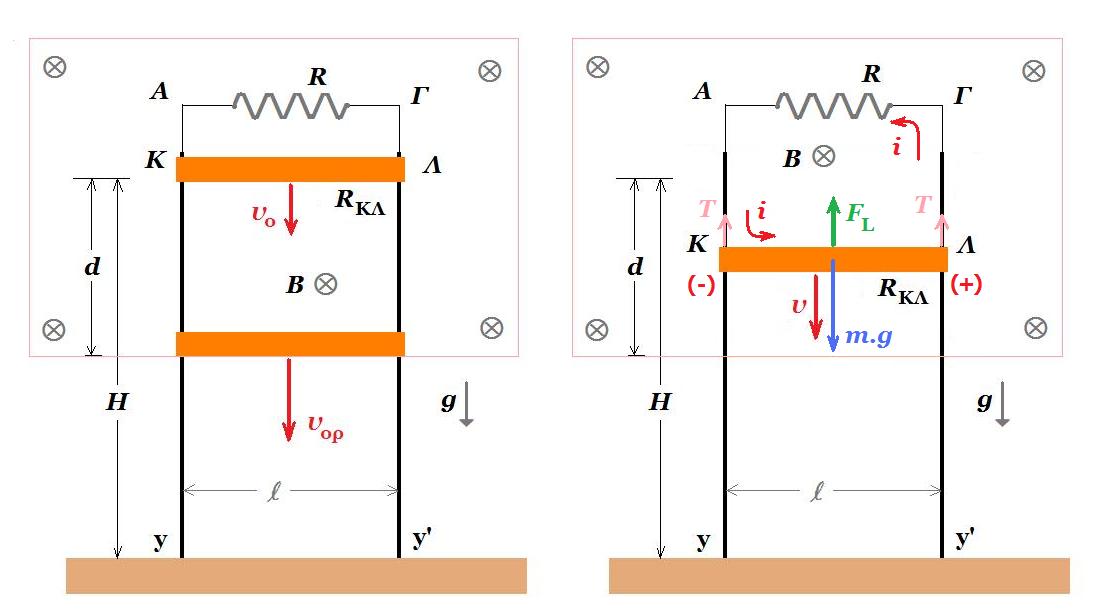
Δ1. Eεπαγ = Β . υ . l = i . ( R + RΚΛ ) => i = Β . υ . l / ( R + RΚΛ )
FL = B . i . l => FL = B2 . l2 . v / ( R + RΚΛ )
ΣF = m . a => m.g - T - FL = m.a => m.g - T - B2.l2. vορ / (R + RΚΛ) = 0 =>
=> vορ = (m.g - T).(R + RΚΛ) / B2.l2 => vορ = (0,2 . 10 - 1).0,5 / 0,52.12 => vορ = 2 m/s
Kεξόδου = ½ m voρ2 = ½ . 0,2 . 22 = 0,4 J
Καρχική = ½ m vo2 = ½ 0,2 1 = 0,1 J WT = T d = 1 4 = 4 J mg d = 2 4 = 8 J WFL = 0,1 + 8 - 4 - 0,4 = 3,7 J
Δ2. VΛΚ = i . R => 0,15 V = i . 0,1 Ω => i = 1,5 A FL = B . i . l = 0,5 . 1,5 . 1 = 3/4 N
m.g - T - FL = m.a => 2 - 1 - 0,75 = 0,2.a => 0,25 = 0,2.a => a = 1,25 m/s2
i = Β υ l / ( R + RΚΛ ) => 1,5 = 0,5 υ 1 / 0,5 => v = 1,5 m/s
dK / dt = m a v = 0,2 1,25 1,5 => dK/dt = 0,375 J/s
Δ3. ΣF = m . a => m.g - T - FL = ma => mg - T - B2l2 v / (R + RΚΛ) = m a =>
=> 2 - 1 - 0,25 v / 0,5 = 0,2 a => 5 - 2,5 v = a
Δ4. QT = T H = 1 N 6 m => QT = 6 J
QR = WFL = ½ m vo 2 + mg d - Τ d - ½ m voρ 2 =
= ½ . 0,2 .12 + 0,2.10.4 - 1.4 - ½ . 0,2 .22 = 0,1 + 8 - 4 - 0,4 => QR = WFL = 3,7 J
όταν η ράβδος βγει από το μαγνητικό πεδίο δεν κυκλοφορεί ρεύμα στο κύκλωμα

ΟΕΦΕ 2020.
Ισοπαχής οριζόντια ομογενής δοκός ΑΓ μήκους l = 1 m και μάζας Μ = 2 kg αρθρώνεται στο άκρο της Α σε κατακόρυφο τοίχο. Η δοκός ισορροπεί οριζόντια μέσω αβαρούς , μη εκτατού νήματος το οποίο συνδέεται με το μέσον της Δ ενώ η άλλη άκρη του καταλήγει στον κατακόρυφο τοίχο. Στο άλλο άκρο Γ της δοκού έχει στερεωθεί το επάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 50 N/m ενώ στο άλλο άκρο έχει δεθεί σφαίρα Σ1 μάζας m1 = 0,5 kg. Mέσω αβαρούς , μη εκτατού νήματος η σφαίρα Σ1 συνδέεται με το μέσο αγώγιμης ομογενούς ράβδου ΚΛ μάζας m2 = 1,5 kg μήκους l = 2 m και ωμικής αντίστασης RΚΛ = 3 Ω. Η ράβδος ΚΛ βρίσκεται σε επαφή με λεία κατακόρυφα σύρματα ΣΣ1 και Σ'Σ2 μεγάλου μήκους αμελητέας ωμικής αντίστασης τα οποία απέχουν σταθερή απόσταση l=2m. Τα κάτω άκρα Σ1 και Σ2 των δύο συρμάτων συνδέονται με αντίσταση R = 1 Ω. Ένα μέρος της διάταξης των συρμάτων ΣΣ1 και Σ'Σ2 βρίσκεται μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης Β = 2 Τ με δυναμικές γραμμές κάθετες στο επίπεδο κινήσεως της ράβδου.
Κάποια στιγμή κόβουμε το νήμα που συνδέει τη σφαίρα με τη ράβδο. Η σφαίρα εκτελεί απλή αρμονική ταλάντωση με σταθερά επαναφοράς D = k ενώ η ράβδος κινείται κατακόρυφα κατερχόμενη σε επαφή πάντα με τα σύρματα ΣΣ1 και Σ'Σ2 .
Δ1. Να βρεθεί η απόσταση μεταξύ των δύο θέσεων της ταλάντωσης της σφαίρας Σ1 για τις οποίες ισχύει ότι η κινητική ενέργεια είναι τριπλάσια της δυναμικής ενέργειας της ταλάντωσης.
Δ2. Εκφράστε την δύναμη από το ελατήριο συναρτήσει του χρόνου.
Δ3. Υπολογίστε την δύναμη που ασκεί η άρθρωση στη δοκό όταν η σφαίρας Σ1 βρεθεί στο ανώτερο σημείο της τροχιάς της.
Τη στιγμή που η ταχύτητα της σφαίρας Σ1 μηδενίζεται για δεύτερη φορά μετά το κόψιμο του νήματος, η ράβδος ΚΛ εισέρχεται στο χώρο του μαγνητικού πεδίου.
Δ4. Υπολογίστε την Εεπαγ που αναπτύσσεται στα άκρα της ΚΛ, την επιτάχυνση της ράβδου και τον ρυθμό μεταβολής της δύναμης Laplace.
Δ5. Υπολογίστε την οριακή ταχύτητα της ράβδου και βρείτε μαθηματική σχέση της επιτάχυνσης α σε σχέση με την ταχύτητα υ.
Θεωρούμε χρονική στιγμή t0 = 0 τη στιγμή που η ράβδος αποκτά οριακή ταχύτητα. Τότε απέχει από τη βάση Σ1Σ2 απόσταση h = 10 m.
Δ6. Μετά από χρονική διάρκεια Δt από την στιγμή t0 το ηλεκτρικό φορτίο που διέρχεται από μια διατομή της ράβδου ΚΛ έχει τιμή q = 7,5 C. Υπολογίστε πόσο απέχει η ράβδος από τη βάση Σ1Σ2 και να γράψετε την εξίσωση του μέτρου της μαγνητικής ροής που διέρχεται από το κλειστό κύκλωμα συναρτήσει του χρόνου για την παραπάνω χρονική διάρκεια.
Οι αντιστάσεις αέρα αμελητέες.
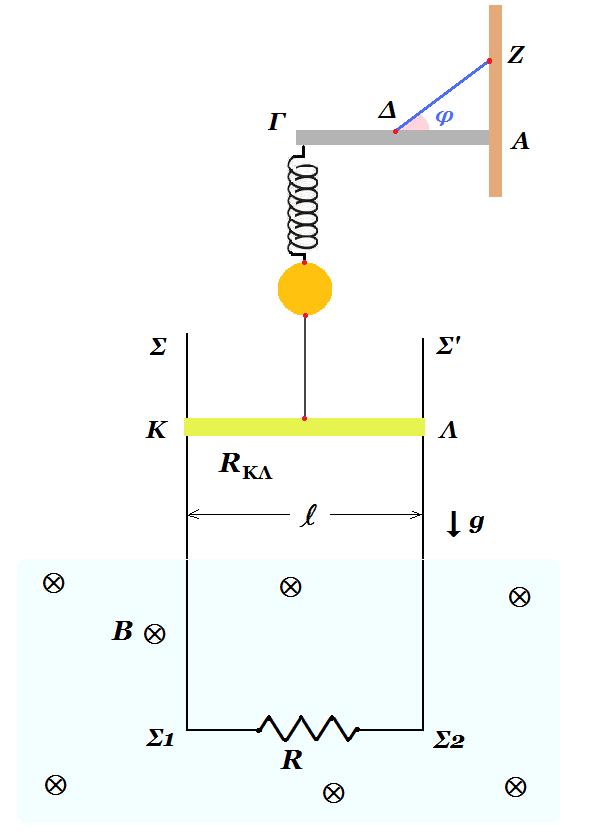
Δ1.
ισορροπία δοκού ΑΓ : ΣFx = TΔ(x) - FA(x) = 0 (1)
ΣFy = M.g + Fελατ - TΔ(y) + FA(y) = 0 (2)
ροπές ως προς Δ : Fελατ .(ΓΔ) - FA(y) .(ΔΑ) = 0 => Fελατ = FA(y) (3) (ΓΔ) = (ΔΑ) = (ΑΓ)/2
ροπές ως προς Α : Fελατ .(ΑΓ) + M.g .(ΔΑ) - TΔ(y) .(ΔΑ) = 0 => 2.Fελατ + M.g - TΔ(y) = 0 (4)
ισορροπία σφαίρας : m1.g - Fελατ + T = 0 (5)
ισορροπία ράβδου ΚΛ : m2.g - T = 0 => Τ = 15 Ν
(5) => Fελατ = 5 + 15 => Fελατ = 20 Ν k.Δl = Fελατ => Δl = 20/50 => Δl = 0,4 m
(4) => TΔ(y) = 2.20 + 20 => TΔ(y) = 60 Ν
(3) => FA(y) = 20 Ν
Δ2.
τη στιγμή που κόβουμε το νήμα το ελατήριο είναι επιμηκυμένο κατά Δl = 0,4 m
ισορροπία σφαίρας : m1.g = Fελατ = k.x1 => x1 = 5/50 = 0,1 m άρα A = Δl - x1 = 0,3 m
ω2 = k / m1 = 50 / 0,5 => ω = 10 rad/s Τ = 2π/ω = π/5 s
x(t) = 0,3 ημ(10.t + π/2) v(t) = 3 συν(10.t + π/2) α(t) = -30 ημ(10.t + π/2)
ΣF = m1 . a => m1.g + Fελατ = m1 . a => Fελατ = m1 .a - m1.g =>
=> Fελατ (t) = -15 ημ10.t - 5 = - k.x(t) - 5
Κ = 3.U => U = E/4 => x = ± A/2 = ± 0,15 m
η απόσταση της θέσης x = - 0,15 m από τη θέση x = + 0,15 m είναι 0,3 m
Δ3.
τη στιγμή που η σφαίρα είναι στο ανώτατο σημείο της τροχιάς της το ελατήριο είναι συσπειρωμένο κατά 0,2 m
x = - 0,3 m => Fελατ = - k.x - 5 = - 50 . (-3) - 5 = 15 - 5 = +10 N η δοκός δέχεται δύναμη από το ελατήριο - 10 Ν (προς τα πάνω)
(3) => FA(y) = Fελατ = 10 Ν (προς τα πάνω)
(4) => 2.Fελατ + M.g - TΔ(y) = 0 => 2.(-10) + 20 - TΔ(y) = 0 => TΔ(y) = Τ ημφ = 0 άρα Τ = 0
(1) => FA(x) = TΔ(x) = Τ συνφ = 0
συνεπώς η δοκός στην άρθρωση Α δέχεται δύναμη FA(y) = Fελατ = 10 Ν (προς τα πάνω)
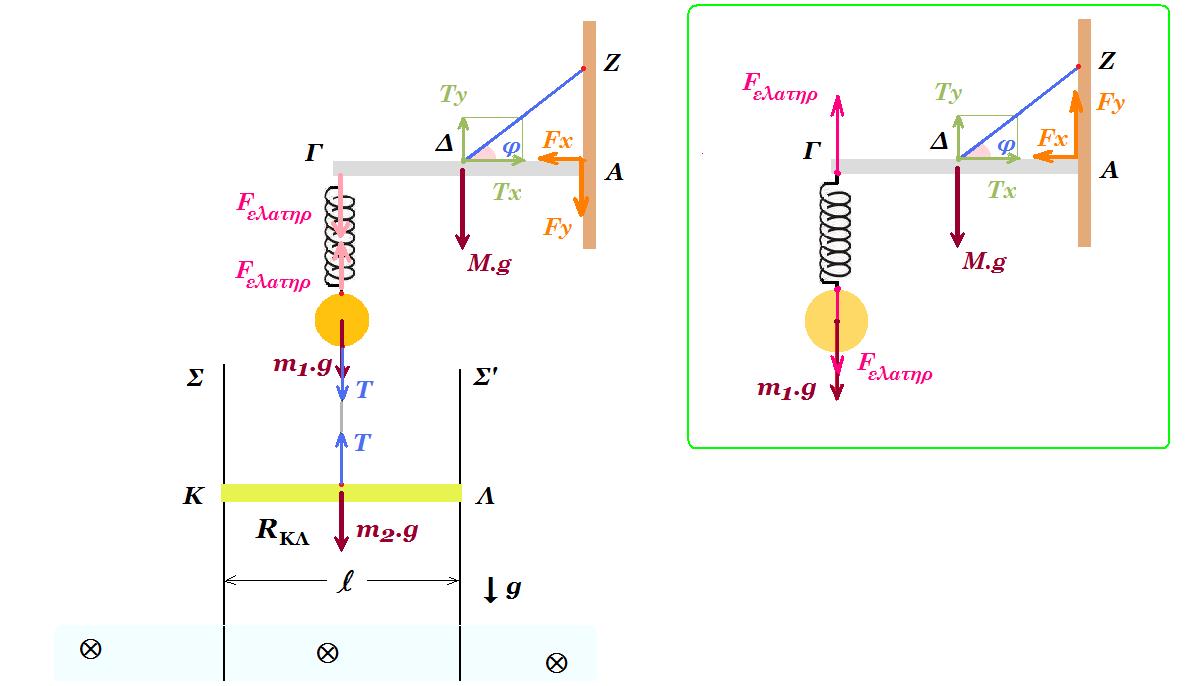
Δ4.
v(t) = 3 συν(10t + π/2) = 0 => συν(10t + π/2) = 0 = συν(π/2) => 10t + π/2 = Νπ + π/2 Ν=1,2,3,...
Ν = 1 : t = π/10 s , Ν = 2 : t = π/5 s = Τ , Ν = 3 : t = 3π/10 s , ...
η ράβδος κάνει ελεύθερη πτώση : υ = g . t, y = ½ . g . t2
υ = g . t = 10 . π/5 => v = 2π m/s Eεπαγ = Β . υ . l = 2 . 2π . 2 => Eεπαγ = 8π Volt
y = ½ . g . t2 = ½ . 10 . (π/5)2 = 5 . 10 / 25 => y = 2 m η ράβδος σε χρόνο π/5 s έχει διανύσει 2 m και έχει αποκτήσει ταχύτητα 2π m/s
Eεπαγ = Β . υ . l = i .( R + RΚΛ ) => i = 8π / (1 + 3) => i = 2π A
FL = B . i . l => FL = 2 . 2π . 2 => FL = 8π Ν
ΣF = m2 . a => m2 .g - FL = m2 .a => 15 - 8π = 1,5 . a => a = 10 - 16π/3 m/s2 < 0 επιβράδυνση
dFL / dt = FL . v . συνπ = 8π Ν . 2π m/s . (-1) = - 16π2 = - 160 => dFL / dt = - 160 J/s τα διανύσματα FL και v είναι αντίρροπα
Δ5.
Eεπαγ = Β . υ . l = i . ( R + RΚΛ ) => i = Β . υ . l / ( R + RΚΛ )
FL = B . i . l => FL = B2 . l2 . v / ( R + RΚΛ )
ΣF = m2 . a => m2 .g - FL = m2 .a => m2 .g - B2.l2. vορ / (R + RΚΛ) = 0 =>
=> vορ = m2 .g.(R + RΚΛ) / B2.l2 => vορ = 1,5 . 10 . 4 / 22.22 => vορ = 15/4 m/s επειδή αρχικά FL = 8π Ν > m.g = 15 Ν η ράβδος ΚΛ θα κινηθεί επιβραδυνόμενα μέχρι α = 0 επειδή συν τω χρόνω αυξάνεται η ταχύτητά της, οπότε θα αποκτήσει οριακή ταχύτητα
m2 .g - FL = m2 .a => m2 .g - B2.l2.v/(R + RΚΛ) = m2 .a => 15 - 22.22.v/(1 + 3) = 1,5 .a => a = 10 - 8/3.v
υ = 2π α = 10 - 16π/3 υ = 15/4 α = 10 - 8/3 . 15/4 = 10 - 10 = 0
Δ6.
η ράβδος κινείται με σταθερή ταχύτητα vορ = 15/4 m/s σε χρονικό διάστημα Δt διανύει Δx = vορ Δt το φορτίο που διέρχεται από το κλειστό κύκλωμα είναι 7,5 C = q = ΔΦ / ( R + RΚΛ ) => 7,5 C = ΔΦ / 4 Ω => ΔΦ = 30 Wb αλλά ΔΦ = Β A = B l Δx = B l vορ Δt => 30 Wb = 2 T 2 m 15/4 m/s Δt => Δt = 2 s οπότε η ράβδος έχει διανύσει Δx = vορ Δt = 15/4 m/s 2 s = 7,5 m άρα απέχει 2,5 m από την βάση Σ1Σ2
η μαγνητική ροή δίνεται από τη σχέση : Φ(t) = Β A = B l x = B l ( h - vορ t ) => 2 T 2 m ( 10 m - 15/4 m/s t ) = 40 - 15t
.............................................................................................................................................................................
μελέτη α(v) a(t) v(t) x(t)
a = 10 - 8/3.v => dv/dt = -8/3.(v - 30/8) => dv/dt = -8/3.(v - 15/4) => dv/(v-15/4) = -8/3.dt =>
=> ln { (v - 15/4) / (2π - 15/4) } = -8/3.t => (v - 15/4) / (2π - 15/4) = e-8/3.t =>
=> (v - 15/4) = (2π - 15/4).e-8/3.t => v(t) = 15/4 + (2π - 15/4).e-8/3.t
τ = 3/8 s 5τ = 15/8 s e0 = 1 e-8/3.15/8 = e-5 = 0,0067
v(0) = 15/4 + (2π - 15/4).e-8/3.0 = 15/4 + 2π - 15/4 = 2π m/s αρχική τιμή
v(15/8) = 15/4 + (2π - 15/4).e-5 = 15/4 + (2π - 15/4).0,0067 = 15/4 - 0,017 = 15/4 m/s = υορ
a(t) = dv(t) / dt = -8/3. (2π - 15/4).e-8/3.t
α(0) = -8/3.(2π - 15/4).e-8/3.0 = -8/3.(2π - 15/4) . 1 = -16π/3 + 10 m/s2 αρχική τιμή
α(15/8) = -8/3.(2π - 15/4).e-5 = -8/3.(2π - 15/4).0,0067 = -8/3 . 0,017 = 0,045 m/s2 = 0
dx = v . dt => dx = [ 15/4 + (2π - 15/4).e-8/3.t ] dt =>
=> x = 15/4.t - 3/8.(2π - 15/4). { e-8/3.t - e0 } =>
x(t) = 15/4.t - 3/8.(2π - 15/4). { e-8/3.t - 1 } x(0) = 0
x(15/8) = 15/4. 15/8 - 3/8.(2π - 15/4). { e-8/3.15/8 - 1 } = 7 - 3/8.(2π - 15/4). { 0,0067 - 1 } =
= 7 - 3/8 . 2,53 . (-1) = 7 + 0,95 = 8 m
η ράβδος εισέρχεται στο μαγνητικό πεδίο με ταχύτητα 2π m/s δέχεται δύναμη Laplace και επιβραδύνεται αρχικά με (10 -16π/3) m/s2 αργότερα αποκτά οριακή ταχύτητα 15/4 m/s = υορ έχοντας επιτάχυνση α = 0 ενώ διάνυσε κατακόρυφη απόσταση 8 m.
...............................................................................................................................
ΟΕΦΕ 2020

ΘΕΜΑ Γ
Δυο παράλληλοι, οριζόντιοι μεταλλικοί αγωγοί Αx1 και Γx2 μεγάλου μήκους, έχουν αμελητέα ωμική αντίσταση και απέχουν μεταξύ τους σταθερή απόσταση l = 2 m. Τα άκρα τους Α και Γ συνδέονται μέσω του κυκλώματος των αντιστατών R1, R2 με τιμές ωμικών αντιστάσεων 3 Ω και 6 Ω αντίστοιχα. Ευθύγραμμος αγωγός ΚΛ μήκους l = 2 m και ωμικής αντίστασης R = 1 Ω , μπορεί να ολισθαίνει χωρίς τριβές, με τα άκρα του συνεχώς σε επαφή με τους οριζόντιους αγωγούς Αx1 και Γx2 . Η όλη διάταξη βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο, κάθετο στο επίπεδο που ορίζουν οι οριζόντιοι αγωγοί Αx1 και Γx2 . Αρχικά ο αγωγός ΚΛ συγκρατείται ακίνητος (θέση (1) ) και ο διακόπτης δ είναι ανοιχτός. Τη χρονική στιγμή t0 = 0 ασκείται στον αγωγό ΚΛ σταθερή οριζόντια δύναμη F μέτρου 6 Ν , παράλληλη στα σύρματα Αx1 και Γx2 με φορά προς τα δεξιά όπως στο σχήμα, που φαίνεται η κάτοψη της διάταξης.
Μετά από κάποιο χρονικό διάστημα, η ένταση του ηλεκτρικού ρεύματος στο κύκλωμα αποκτά σταθερή τιμή i = 3 A, με φορά στον αγωγό ΚΛ, από το σημείο Λ προς το σημείο Κ (θέση (2)).
Γ1. Να προσδιορίσετε τη φορά και την τιμή της έντασης του ομογενούς μαγνητικού πεδίου.
Γ2. Να δικαιολογήσετε γιατί η ενέργεια που προσφέρει στη διάταξη η δύναμη F μέσω του έργου της, μεταξύ των θέσεων (1) και (2), έχει μεγαλύτερη τιμή, από την τιμή της κινητικής ενέργειας του αγωγού ΚΛ στη θέση(2).
Γ3. Όταν ο αγωγός ΚΛ κινείται με ταχύτητα μέτρου υ = 2 m/s να υπολογίσετε τη διαφορά δυναμικού VKΛ στα άκρα του αγωγού και το ρυθμό μεταβολής της κινητικής του ενέργειας τότε.
Κάποια στιγμή και αφού ο αγωγός ΚΛ έχει περάσει από τη θέση (2) κλείνουμε τον διακόπτη δ, χωρίς να σχηματισθεί σπινθήρας.
Γ4. Αμέσως μετά το κλείσιμο του διακόπτη δ, να μελετηθεί η κίνηση που θα εκτελέσει ο αγωγός και να υπολογίσετε τη μικρότερη τιμή της ηλεκτρικής ισχύος που καταναλώνεται στο σύστημα των αντιστατών R1 και R2 .
Γ1. F - B l i = m a => 6 - B 2 Bv/2 = m a FL = F => B l i = F => B 2m 3A = 6N => B = 1T η ένταση του ρεύματος είναι από το Λ προς το Κ η δύναμη Laplace είναι αντίρροπη της F η φορά του μαγνητικού πεδίου είναι προς τα μέσα B l v = i (R + R1) => 1 2 v = 3 4 => v = 6 m/s = vορ οριακή ταχύτητα
Γ2. ένα μέρος της ενέργειας που προσφέρει η δύναμη F μετατρέπεται σε θερμότητα πάνω στις αντιστάσεις
Γ3. v = 2 m/s E = B l v = 1 2 2 = 4 Volt B l v = i (R + R1) => 1 2 2 = i (1 + 3) => i = 1A
VΚΛ = Ε - i (R + R1) = 4 - 1 (1 + 3) = 0 Volt
F - B l i = m a => 6 - 1 2 1 = m a => m a = 4 N dK/dt = m v a = m a v = 4N 2m/s = 8 J/s
ΟΕΦΕ 2019 Β' φάση
ΘΕΜΑ Δ
Λεπτή ομογενής ράβδος ΑΓ μάζας m = 2 kg μήκους l = 1 m μπορεί να περιστρέφεται χωρίς τριβές γύρω από σταθερό οριζόντιο άξονα κάθετο στο επίπεδό της που διέρχεται από το άκρο της Α. Η ράβδος ισορροπεί οριζόντια με τη βοήθεια κατακόρυφου μη εκτατού νήματος που είναι δεμένο στο άκρο της Γ. Το νήμα είναι τυλιγμένο πολλές φορές στο αυλάκι διπλής τροχαλίας μάζας Μ = 2 kg που αποτελείται από δύο ομογενείς δίσκους με ακτίνες R και 2R. Οι δύο δίσκοι συνδέονται μεταξύ τους ώστε να περιστρέφονται ως ένα σώμα χωρίς τριβές γύρω από οριζόντιο ακλόνητο άξονα που διέρχεται από το κέντρο τους Κ και είναι κάθετος στο επίεδό τους. Στο αυλάκι του δίσκου ακτίνας R έχουμε τυλίξει αβαρές μη εκτατό νήμα μεγάλου μήκους στο ελεύθερο άκρο του οποίου έχουμε δέσει σώμα Σ1. Το σύστημα << ράβδος - διπλή τροχαλία - σώμα Σ1 >> ισορροπεί ακίνητο. Θεωρούμε θετική κατεύθυνση προς τα κάτω.
Δ1. Υπολογίστε τη μάζα του σώματος Σ1. Πόση δύναμη δέχεται η ράβδος από την άρθρωση στο άκρο της Α; Πόση δύναμη δέχεται η τροχαλία στο κέντρο της Κ;
Τη στιγμή t = 0 κόβεται το νήμα που συνδέει τη ράβδο με τη διπλή τροχαλία. Αμέσως μετά η τροχαλία και η ράβδος αρχίζουν να περιστρέφονται χωρίς το νήμα να γλιστράει στο αυλάκι του δίσκου ακτίνας R.
Τη χρονική στιγμή t1 όπου το σώμα Σ1 έχει διανύσει κατακόρυφη απόσταση h = 1 m ο ρυθμός μεταβολής της κινητικής του ενέργειας είναι dK/dt = 8 J/s, το νήμα κόβεται. Αμέσως μετά το σώμα Σ1 συγκρούεται κεντρικά - πλαστικά με σώμα Σ2 μάζας m2 = 2 kg που ταλαντώνεται με εξίσωση x(t) = 0,2 ημ(ωt) στο επάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 100 N/m. Στο άλλο άκρο του ελατηρίου είναι δεμένο σώμα Σ3 μάζας m3 = 5 kg που είναι ακίνητο στο οριζόντιο έδαφος. Τη στιγμή της κρούσης το Σ2 βρίσκεται στο χαμηλότερο σημείο της ταλάντωσής του. Αμέσως μετά την κρούση το συσσωμάτωμα αρχίζει να εκτελεί απλή αρμονική ταλάντωση με σταθερά D = k.
Δ2. Υπολογίστε το πλάτος της ταλάντωσης του συσσωματώματος.
Δ3. Εκφράστε την δύναμη Ν που δέχεται το σώμα Σ3 από το έδαφος συναρτήσει του χρόνου. Θεωρείστε t=0 όταν αρχίζει να ταλαντώνεται το συσσωμάτωμα

Δ1.
ισορροπία Σ1 : ΣFy = 0 => m1 g = T1 (1)
ισορροπία τροχαλίας : ΣFy = 0 => M g + Τ1 + T2 + F(K) = 0 (2)
ροπές ως προς Κ : Τ1 R = T2 2R => Τ1 = 2T2 (3)
ισορροπία ράβδου : ΣFy = 0 => mg - T2 + F(A) = 0 (4)
ροπές ως προς A : mg l/2 = T2 l => T2 = mg/2 = 2.10/2 => T2 = 10 N
οπότε από (3) => T1 = 20 N από (1) => m1 = 2 kg
(2) => 2 10 + 20 + 10 + F(K) = 0 => F(K) = -50 Ν κατακόρυφη προς τα πάνω
(4) => 2 10 - 10 + F(A) = 0 => F(Α) = -10 Ν κατεύθυνση κατακόρυφη προς τα πάνω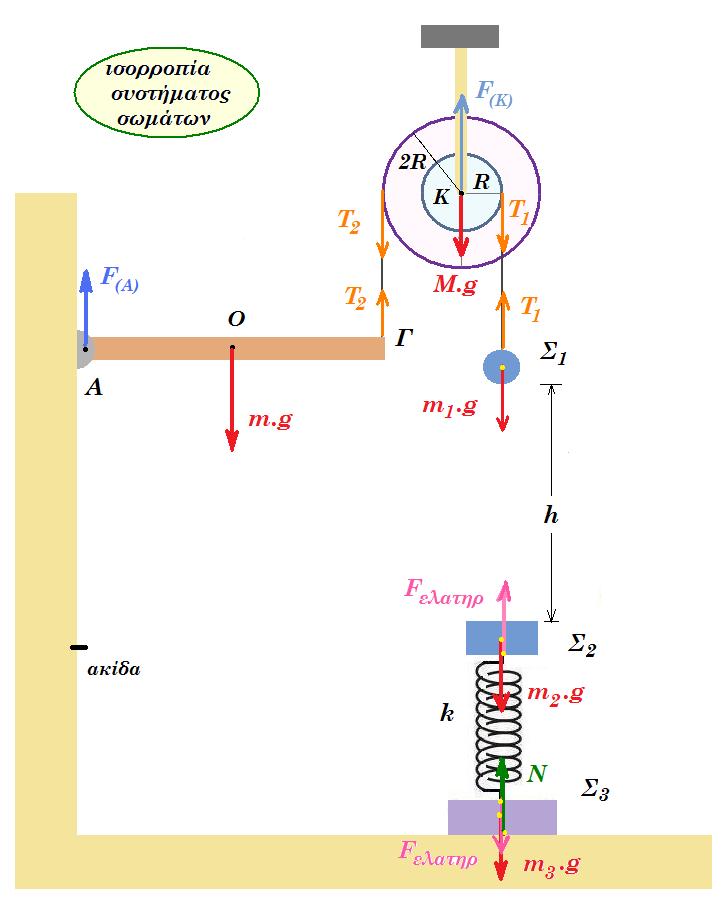
Δ2.
κατακόρυφη κίνηση Σ1 : ΣFy = m1 a1 => m1 g - T1 = m1 a1 (5)
περιστροφή τροχαλίας : aγων R = a1 (6)
dK/dt = m1 v1 a1 = m1 a1 t a1 => dK/dt = m1 a12 t (7)
h = ½ α1 t2 => h2 = 1/4 a12 t4 (8)
dK/dt / h2 = 4 m1 / t3 => 8 / 12 = 4 2 / t3 => t = 1 s
h = ½ α1 t2 => 1 = ½ α1 12 => a1 = 2 m/s2 v1 = a1 t = 2 m/s πριν την κρούση
το σώμα Σ2 ταλαντώνεται και τη στιγμή της κρούσης είναι στο κατώτερο σημείο της ταλάντωσής του άρα η ταχύτητά του είναι μηδέν
πλαστική κρούση διατήρηση ορμής : m1 v1 = ( m1 + m2 ) v1,2 => v1,2 = 1 m/s
ισορροπία m2 : m2 g = Fελατ = k x2 => x2 = 2 10 / 100 = 0,2 m συσπείρωση
ισορροπία ( m1 + m2 ) : (m1 + m2) g = Fελατ = k x1,2 => x1,2 = 4 10 / 100 = 0,4 m συσπείρωση
ω2 = k / ( m1 + m2 ) = 100 / 4 => ω = 5 rad/s
ω2 = k / m1 = 100 / 2 => ω = 5√2 rad/s Τ = 2π / 5√2 = 0,8886 s x = 0,2 ημ(5√2t)
το σώμα Σ2 ταλαντώνεται και τη στιγμή της κρούσης είναι στο κατώτερο σημείο της ταλάντωσής του άρα η ταχύτητά του είναι μηδέν και είναι στη Θ.Ι. του συσσωματώματος δηλαδή το ελατήριο έχει συσπείρωση 0,4 m
διατήρηση ενέργειας για την ταλάντωση : ½ k 02 + ½ ( m1 + m2 ) v1,2 2 = ½ k A2 =>
=> 4 1 = 100 A2 => Α2 = 0,04 => A = 0,2 m
Δ3.
όταν συγκρούονται τα Σ1 και Σ2 το συσσωμάτωμα έχει ταχύτητα v1,2 = 1 m/s προς τα κάτω και είναι στη Θ.Ι. του θεωρούμε t = 0 όταν αρχίζει να ταλαντώνεται το συσσωμάτωμα
x(t) = 0,2 ημ(5t) υ(t) = 1 συν(5t) α(t) = -5 ημ(5t)
ΣF(t) = m1,2 a = 4 ( -5 ημ(5t) ) = - 20 ημ(5t)
ΣF = m1,2 a => Fελατ + m1,2 g = m1,2 a => Fελατ = m1,2 a - m1,2 g =>
=> Fελατ(t) = - 20 ημ(5t) - 40 δέχεται το συσσωμάτωμα Fελατ(0) = - 40 Ν = - m1,2 g
το ελατήριο είναι συσπειρωμένο κατά 0,4 m
Fελατ(x) = - 100 (0,4 + x) - 0,2 m £ x £ + 0,2 m
F'ελατ(t) = + 20 ημ(5t) + 40 δέχεται το σώμα Σ3 F'ελατ(0) = + 40 Ν
F'ελατ(x) = + 100 (0,4 + x) - 0,2 m £ x £ + 0,2 m
ισορροπία m3 : m3 g + F'ελατ - Ν = 0 => 5 10 + 20 ημ(5t) + 40 - Ν = 0 =>
=> Ν(t) = 90 + 20 ημ(5t)
Ν(0) = 90 Ν = 50 + 40 = m3 g + F'ελατ(0)
ισορροπία m3 : m3 g + F'ελατ - Ν = 0 => 5 10 + 100 (0,4 + x) - Ν = 0 =>
=> Ν(x) = 90 + 100x - 0,2 m £ x £ + 0,2 m
N(-0,2) = 70 N το συσσωμάτωμα είναι στο άνω άκρο το ελατήριο είναι συσπειρωμένο 0,2 m
N(+0,2) = 110 N το συσσωμάτωμα είναι στο κάτω άκρο το ελατήριο είναι συσπειρωμένο 0,6 m

ΟΕΦΕ 2016
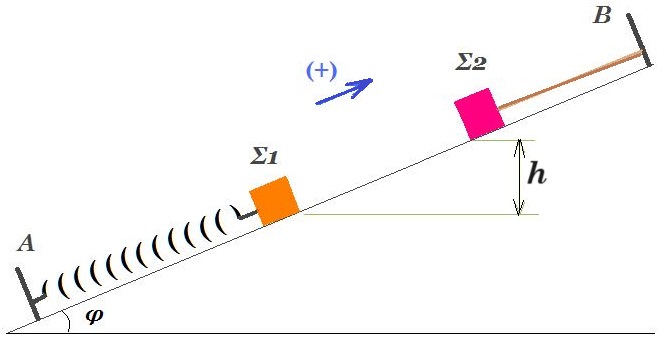
Το στερεό σώμα κυκλικής διατομής έχει εξωτερική ακτίνα R = 0,2 m & μάζα m = 4 kg. Στο σώμα υπάρχει εσωτερικό αυλάκι με ακτίνα r = 0,1 m. Το στερεό βρίσκεται πάνω σε κεκλιμένο επίπεδο γωνίας κλίσης φ = 30°. Λεπτό αβαρές νήμα είναι τυλιγμένο στο εσωτερικό αυλάκι και δεν ολισθαίνει σε όλη τη διάρκεια του φαινομένου που ακολουθεί. Στην άκρη του νήματος που παραμένει συνεχώς παράλληλο με το κεκλιμένο επίπεδο ασκείται σταθερή δύναμη παράλληλη με το κεκλιμένο επίπεδο μέσω της οποίας ελέγχουμε την κίνηση του σώματος. 
Δ1. Υπολογίστε το μέτρο της δύναμης F ώστε το στερεό να ισορροπεί ακίνητο πάνω στο κεκλιμένο επίπεδο.
Δ2. Αυξάνουμε το μέτρο της δύναμης F κατά 30% και το στερεό αρχίζει να κυλίεται χωρίς να ολισθαίνει. Έστω το μέτρο της επιτάχυνσης του κέντρου μάζας του στερεού ισούται με 1 m/s2 υπολογίστε την γωνιακή επιτάχυνση του στερεού καθώς και την συνολική ροπή που δέχεται το στερεό, ως προς το κέντρο του Ο.
Δ3. Τη στιγμή t1 όπου το στερεό έχει μετατοπιστεί κατά Δx = 2 m από την αρχική του θέση υπολογίστε το μέτρο της ταχύτητας του κέντρου μάζας του.
Δ4. Υπολογίστε το έργο που παράγεται από την δύναμη F από την αρχή της διαδικασίας έως την στιγμή t1.
Δ5. Πόση είναι η κινητική ενέργεια του στερεού τη στιγμή t1 ;
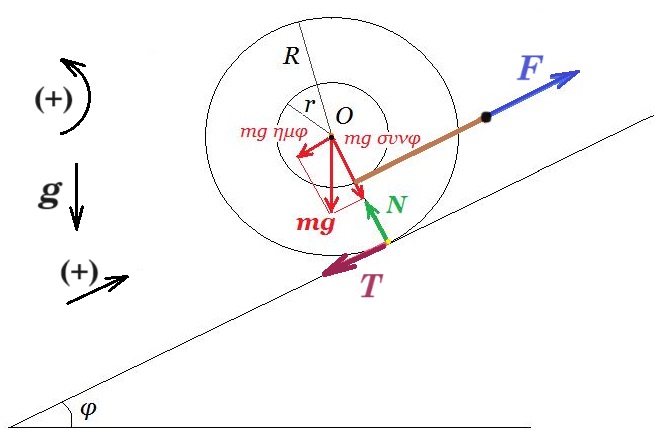
Δ1.
ΣF = 0 => F - T - m g ημφ = 0 (1) ημφ = ημ30° = 0,5
Στ(Ο) = 0 => F r = T R => T = F r / R => T = F 0,1 / 0,2 = F / 2 (2)
(1), (2) => F - F/2 = m g ημφ => F/2 = 4 10 0,5 => F = 40 N
Δ2.
aγων = a / R = 1 m/s2 / 0,2 m = 5 rad/s2
F1 = F + 30% F = 1,3 F = 1,3 40 N = 52 N
ΣF = m a => F1 - T - m g ημφ = m a (3) ημφ = ημ30° = 0,5
F1 - T - m g ημφ = m a => 52 - T - 4 10 0,5 = 4 1 => T = 52 - 20 - 4 => T = 28 N
Στ(Ο) = F r - T R = 52 N 0,1 m - 28 N 0,2 m = 5,2 Nm - 5,6 Nm = - 0,4 Nm
Δ3.
x = ½ a t2 => 2m = 0,5 1m/s2 t2 => t = 2 sec
vcm = a t = 1m/s2 2s = 2 m/s
ω = vcm / R = 2 / 0,2 = 10 rad/s
aγων = a / R = 1 / 0,2 = 5 rad/s2 θ = ½ αγων t2 = ½ 5 22 = 10 rad
l = θ r = 10 rad 0,1 m = 1 m
το σημείο εφαρμογής της F μετατοπίζεται κατά l = θ r = 10 rad 0,1 m = 1 m
το σημείο εφαρμογής της T μετατοπίζεται κατά l = θ R = 10 rad 0,2 m = 2 m
η F ξετυλίγει το νήμα ενώ η Τ τυλίγει το νήμα
Δ4.
το σημείο εφαρμογής της F μετατοπίζεται κατά l = θ r = 10 rad 0,1 m = 1 m
το έργο της F : WF = F θ r = 52 J 10 rad 0,1 m = 52 J
Kπεριστροφής = ½ I(O) ω2 = ½ ½ m R2 (aγων t) 2 = ½ ½ 4 0,22 (5 2)2 = 4 Joule
dK / dt = I(O) ω aγων = ½ m R2 ω aγων = ½ 4 0,22 10 5 = 4 J/s
Δ5.
Kμεταφοράς = ½ m v2 = ½ 4 22 = 8 J Kολική = 4 J + 8 J = 12 J
U = m g h = m g x ημ30° = 4 10 2 ½ = 40 J
WF = K + U => Κ = 52 J - 40 J = 12 J
ΟΕΦΕ 20011
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~`
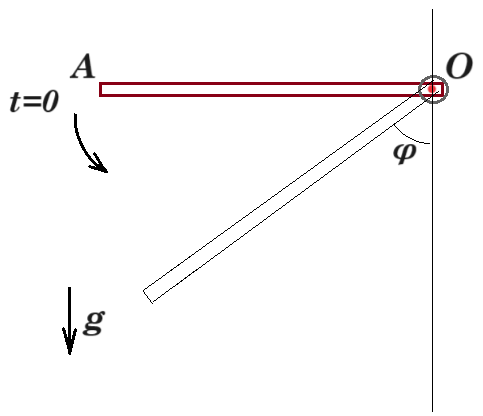
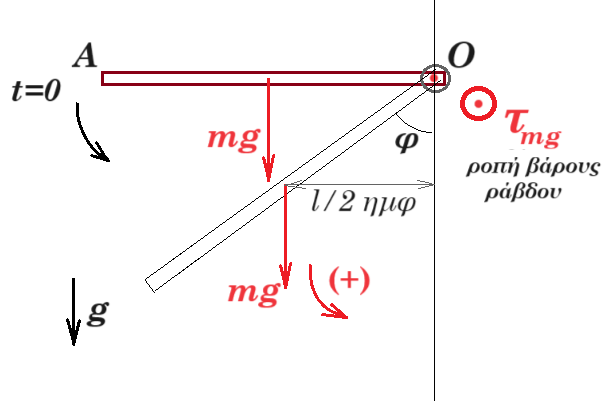
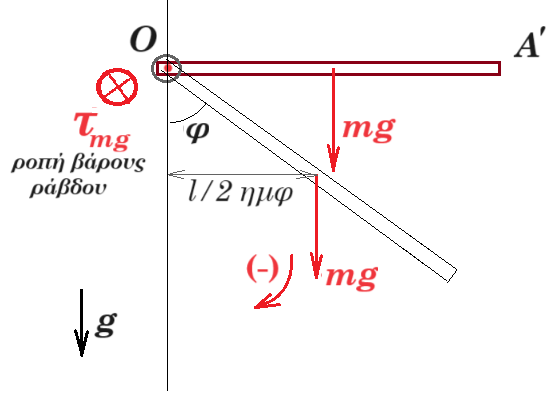
Θεωρούμε ράβδο ΟΑ μάζας M=0,4kg, μήκους l=0,5m, η οποία μπορεί να περιστρέφεται γύρω από οριζόντιο άξονα που διέρχεται από το άκρο της Ο. Φέρνουμε τη ράβδο σε οριζόντια θέση και τη στιγμή t=0 την αφήνουμε ελεύθερη να κινηθεί. Εκφράστε την ροπή που δέχεται η ράβδος ως προς το άκρο της Ο συναρτήσει της γωνίας φ που σχηματίζει η ράβδος με την κατακόρυφο.
 |
 |
 |
Στ(Ο) = Μ g l/2 ημφ = 0,4 10 0,25 ημφ = ημφ
αρχική θέση (ΟΑ) : φ = θ => ημφ = ημθ = 0,8 => Στ(Ο) = +0,8 kg m2/s2
η ράβδος σε κατακόρυφη θέση : φ = 0 => ημφ = 0 => Στ(Ο) = 0
τελική θέση (ΟΑ') : Στ(Ο) = - 0,8 kg m2/s2
όταν η ράβδος στρέφεται κατερχόμενη η ροπή είναι θετική ενώ όταν στρέφεται ανερχόμενη η ροπή είναι αρνητική
όταν η ράβδος διέρχεται από την κατακόρυφη θέση η γωνιακή της ταχύτητα είναι μέγιστη η γωνιακή της επιτάχινση ισούται με μηδέν
όταν κατέρχεται η αγων είναι ομόρροπη της ω αλλά το μέτρο της μειώνεται μέχρι να μηδενισθεί ενώ όταν ανέρχεται η αγων είναι αντίρροπη της ω και το μέτρο της αυξάνεται μέχρι να γίνει μέγιστο όταν η ράβδος έρθει σε οριζόντια θέση (ΟΑ') όπου σταματά στιγμιαία
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
ΟΕΦΕ 2010
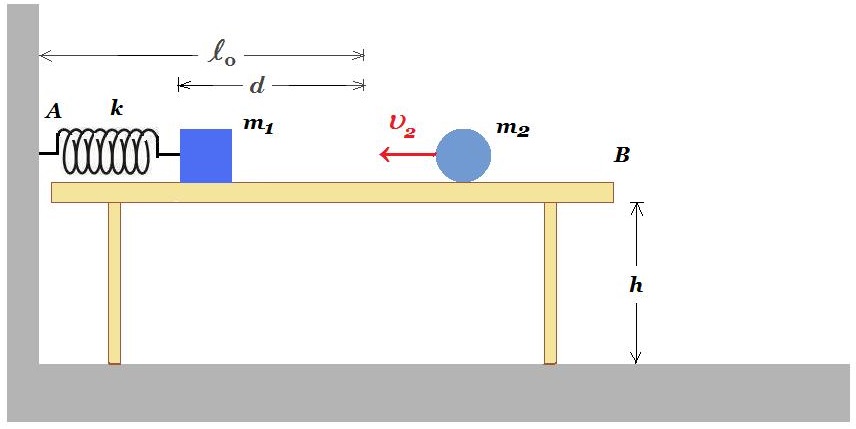
Σώμα Σ μικρών διαστάσεων με μάζα m=1kg ισορροπεί πάνω σε λείο οριζόντιο επίπεδο δεμένο στο άκρο οριζόντιου ελατηρίου σταθεράς k=100N/m και στο άκρο μη εκτατού νήματος αμελητέας μάζας. Το άλλο άκρο του οριζόντιου ελατηρίου είναι ακλόνητα στερεωμένο σε κατακόρυφο τοίχο. Ταυτόχρονα το νήμα είναι στερεωμένο στο άκρο Α ομογενούς και ισοπαχούς ράβδου ΟΑ μάζας M=0,4kg και μήκους l=0,5m. Η ράβδος μπορεί να περιστρέφεται χωρίς τριβές σε κατακόρυφο επίπεδο γύρω από σταθερό οριζόντιο άξονα που είναι κάθετος σε αυτήν και διέρχεται από το άκρο της Ο. Η ράβδος ισορροπεί σχηματίζοντας με την κατακόρυφο γωνία θ με ημθ=0,8 και συνθ=0,6 ενώ το ελατήριο στην παραπάνω θέση έχει δυναμική ενέργεια U=0,32J. 
Τη χρονική στιγμή t = 0 κόβουμε το νήμα και το σύστημα ελατήριο - σώμα Σ αρχίζει να εκτελεί απλή αρμονική ταλάντωση με σταθερά D = k ενώ η ράβδος αρχίζει να περιστρέφεται. Θεωρώντας ως δεδομένο ότι πριν κόψουμε το νήμα όλα τα σώματα της διάταξης βρίσκονται στο ίδιο κατακόρυφο επίπεδο και ότι το σώμα Σ διατηρεί συνεχώς επαφή με το οριζόντιο επίπεδο να :
(α) υπολογίσετε το μέτρο της τάσης του νήματος πριν κόψουμε το νήμα καθώς και τη δύναμη που ασκείται στη ράβδο ΟΑ στο σημείο Ο
(β) γράψετε τη σχέση απομάκρυνσης του σώματος Σ συναρτήσει του χρόνου θεωρώντας ως θετική φορά προς τα δεξιά
(γ) βρεθεί ο ρυθμός μεταβολής της ορμής του σώματος Σ τη στιγμή που η κινητική και η δυναμική ενέργεια της ταλάντωσης θα γίνουν ίσες για πρώτη φορά
(δ) υπολογίσετε την κινητική ενέργεια της ράβδου όταν διέρχεται από την κατακόρυφη θέση
(ε) βρείτε την συνολική ροπή ως προς το άκρο Ο που δέχεται η ράβδος καθώς περιστρέφεται
(A)
U = 0,32 J => U = ½ k Δl2 => ½ 100 Δl2 = 0,32 => Δl2 = 0,0064 => Δl = 0,08 m
ισορροπία σώματος : Τx,Σ - Fελατ = 0 => Τx,Σ - k Δl = 0 => Τx,Σ = 100 0,08 m =>Τx,Σ = 8 N κατεύθυνση οριζόντια προς τα δεξιά
ισορροπία νήματος : Τx,Σ = Τx,Α = 8 N Τx,Α = 8 N κατεύθυνση οριζόντια προς τα αριστερά
Τy,Σ = Τy,Α =>
ισορροπία ράβδου :
ροπές ως προς Ο : Στ(Ο) = 0 => M g l/2 ημθ - Τx,Α l συνθ + Τy,A l ημθ = 0 => 4 1/2 0,8 - 8 0,6 + Τy,A 0,8 = 0 => 1,6 - 4,8 + Τy,A 0,8 = 0 => - 3,2 + Τy,A 0,8 = 0 => Τy,A = 4 Ν κατεύθυνση κατακόρυφη προς τα κάτω
άρα Τy,Σ = 4 Ν κατεύθυνση κατακόρυφη προς τα πάνω
ΣFy = 0 => Μ g + Τy,A + Fy,O = 0 => 0,4 10 + 4 + Fy,O = 0
=> Fy,O = - 8 Ν κατεύθυνση κατακόρυφη προς τα πάνω
ΣFx = 0 => Τx,A + Fx,O = 0 => Fx,O = - 8 N κατεύθυνση οριζόντια προς τα δεξιά
ΤΣ 2 = Τx,Σ 2 + Τy,Σ 2 = 82 + 42 = 64 + 16 = 80 => ΤΣ = √80 Ν = 4 √5 Ν
FO 2 = Fx,O 2 + Fy,O 2 = 82 + 82 = 64 + 64 = 2 64 => FO = 8 √2 Ν

(Β) , (Γ)
U = 0,32 J => U = ½ k Δl2 => ½ 100 Δl2 = 0,32 => Δl2 = 0,0064 => Δl = 0,08 m
ω2 = k / m = 100 / 1 => ω = 10 rad/s f = 10/2π = 5/π Hz T = π/5 s
x(t) = 0,08 ημ(10t + π/2) υ(t) = 0,8 συν(10t + π/2) α(t) = - 8 ημ(10t + π/2) F(t) = m a(t) = - 8 ημ(10t + π/2)
Κ = U = E/2 => x = ± Α / √2 = ± 0,08 / √2 = 0,08 ημ(10 t + π/2) => ημ(10 t + π/2) = ± √2 / 2 για πρώτη φορά : ημ(10 t + π/2) = √2 / 2
dp/dt = F(t) = m a(t) = - 8 ημ(10 t + π/2) = - 8 √2 / 2 = - 4√2 N
(Δ)
h = l/2 - l/2 συνθ = 0,25 ( 1 - 0,6 ) = 0,1 m
M g h = Κτελ => Κτελ = 0,4 10 0,1 = 0,4 J
υΑ = ω l = 2 6½ 0,5 = 6½ m/s
όταν στρέφεται η ράβδος από την αρχική θέση ημθ = 0,8 , η γωνιακή της ταχύτητα αυξάνεται μέχρι να φθάσει σε κατακόρυφη θέση ημθ = ημ0 = 0 , μετά μειώνεται η γωνιακή ταχύτητα έως ότου η ράβδος σχηματίζει μέγιστη γωνία με την κατακόρυφη που εφ' όσον δεν υπάρχουν τριβές και η αντίσταση αέρα είναι αμελητέα, η μεγιστη γωνία είναι η θ : ημθ = 0,8 δηλαδή η ράβδος φθάνει σε συμμετρική θέση ως προς την αρχική της θέση
L = m v R v = ω R v = a t ω = αγων t a = R αγων mg - T = m a dK/dt = m a v
(Ε)
έστω φ η γωνία που σχηματίζει η ράβδος με την κατακόρυφη ενώ στρέφεται, το βάρος της κάνει ροπή ως προς το άκρο της Ο καμία άλλη δύναμη, Στ(Ο) = Μ g l/2 ημφ = 0,4 10 0,25 ημφ = ημφ
αρχική θέση : φ = θ => ημφ = ημθ = 0,8 => Στ(Ο) = +0,8 kg m2/s2
η ράβδος σε κατακόρυφη θέση : φ = 0 => ημφ = 0 => Στ(Ο) = 0
τελική θέση : Στ(Ο) = - 0,8 kg m2/s2
όταν η ράβδος στρέφεται κατερχόμενη η ροπή είναι θετική ενώ όταν στρέφεται ανερχόμενη η ροπή είναι αρνητική
ΟΕΦΕ 2009
Ο δίσκος τροχαλίας είναι ομογενής έχει μάζα Μ = 2 kg ακτίνα R = 0,2 m και ροπή αδράνειας ως προς τον άξονα περιστροφής που περνάει από το κέντρο του Κ και είναι κάθετος στο επίπεδό του Ι(Κ) = ½ Μ R2. Ο άξονας περιστροφής Κ είναι το άκρο αβαρούς ράβδου ΚΑ της οποίας το άλλο άκρο Α είναι στερεωμένο με αρθρωση στην οροφή. Το σύστημα ράβδος - τροχαλία μπορεί να στραφεί περί την άρθρωση Α στο ίδιο κατακόρυφο επίπεδο του δίσκου της τροχαλίας. Τριβές στον άξονα περιστροφής και στην άρθρωση δεν υπάρχουν.
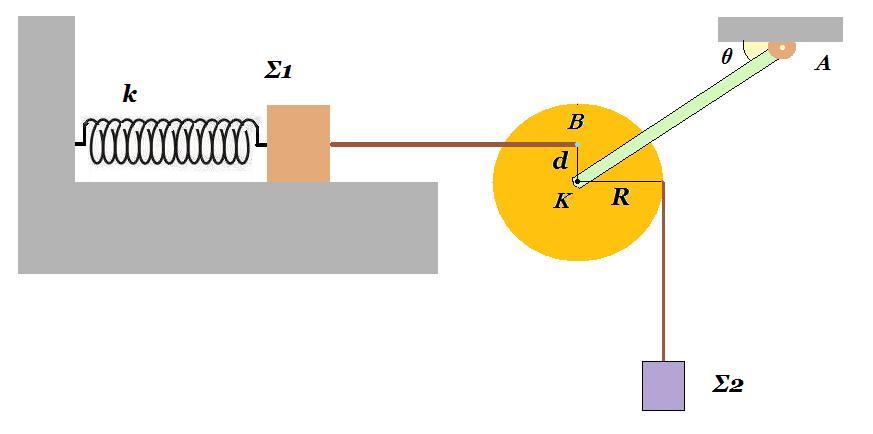
Σώμα Σ1 μάζας m1 = 4 kg είναι προσδεμένο στο ελεύθερο άκρο ιδανικού ελατηρίου σταθεράς k = 100 N/m το άλλο άκρο του οποίου είναι στερεωμένοσε ακλόνητο σημείο. Το σύστημα [ σώμα Σ1 - ελατήριο ] είναι πάνω σε λείο οριζόντιο επίπεδο και στο ίδιο κατακόρυφο επίπεδο που βρίσκεται ο δίσκος της τροχαλίας. Η διάταξη είναι σεισορροπία. Το νήμα που είναι δεμένο το σώμα Σ1 με τον δίσκο της τροχαλίας είναι οριζόντιο. Το σημείο πρόσδεσης Β στον δίσκο της τροχαλίας είναι στην ίδια κατακόρυφο με το Κ και σε απόσταση ΚΒ = d = 0,1 m ενώ η ράβδος ΑΚ σχηματίζει γωνία θ με την οριζόντια οροφή. Το σώμα Σ2 μάζας m2 = 2 kg είναι δεμένο σε νήμα το οποίο έχει τυλιχθεί αρκετές φορές στο αυλάκι του δίσκου της τροχαλίας. Τα νήματα θεωρούνται αβαρή λεπτά και μη εκτατά.
Α. Υπολογίστε το μέτρο της δύναμης που ασκεί η αβαρής ράβδος ΑΚ στον άξονα Κ της τροχαλίας.
Προσδιορίστε την γωνία θ.
Συγκολλούμε την άρθρωση Α ώστε η αβαρής ράβδος να παραμένει ακλόνητη στη θέση που προσδιορίστηκε προηγουμένως και τη στιγμή t = 0 κόβουμε το οριζόντιο νήμα. Τότε το σώμα Σ1 εκτελεί απλή αρμόνική ταλάντωση με D = k και θετική φορά προς τα δεξιά ενώ το σώμα Σ2 κινείται προς τα κάτω. Το κατακόρυφο νήμα στο οποίο είναι δεμένο ξετυλίγεται χωρίς να ολισθαίνει στο αυλάκι του δίσκου της τροχαλίας μένοντας κατακόρυφο.
B. Γράψτε την εξίσωση της απομάκρυνσης της ταλάντωσης του σώματος Σ1 υναρτήσει του χρόνου.
Γ. Τη στιγμή που το σώμα Σ1 περνά από τη θέση ισορροπίας του για δεύτερη φορά να υπολογίσετε τον ρυθμό μεταβολής της κινητικής ενέργειας του σώματος Σ2 και την στροφορμή του αν η γωνιακή επιτάχυνση της τραχαλίας είναι αγων = 100/3 rad/s2 . Πόση είναι η τάση του νήματος εκείνη τη στιγμή;
A.
ισορροπία Σ1 : Fελατ = Τ1 => k Δl = Τ1
ισορροπία Σ2 : m2 g = Τ2 => 2 10 = Τ2 = 20 N
ισορροπία τροχαλίας :
ροπές ως προς Κ : Στ(Κ) = 0 => Τ2 R = T1 d => Τ2 0,2 = T1 0,1 => 2 Τ2 = T1 => Τ1 = 40 N
τότε Δl = Τ1 / k = 40 / 100 => Δl = 0,4 m
ΣFx = 0 => T1 = Fx,K => Fx,K = 40 N
ΣFy = 0 => Μ g + T2 = Fy,K => Fy,K = 2 10 + 20 = 40 N
FK 2 = Fx,K 2 + Fy,K 2 = 40 2 + 40 2 => FK = 40√2 Ν
ισορροπία ράβδου ΑΚ :
ΣFx = 0 => Fx,K = Fx,A => Fx,A = 40 N
ΣFy = 0 => Fy,K = Fy,A => Fy,A = 40 N
FK 2 = Fx,K 2 + Fy,K 2 = 40 2 + 40 2 => FK = 40√2 Ν
εφθ = Fy,A / Fx,A = 40 / 40 =1 => θ = 45°
Β.
ω2 = k / m1 = 100 / 4 = 25 => ω = 5 rad/s T = 2π/ω = 2π/5 s
x(t) = 0,4 ημ(5 t + π/2) v(t) = 2 συν(5 t + π/2) α(t) = - 10 ημ(5 t + π/2)
F(t) = m1 a = - 40 ημ(5 t + π/2)
ΣF = m1 a => Fελατ (t) = - 40 ημ(5 t + π/2) Fελατ (0) = - 40 ημ(π/2) = - 40 N
Γ.
t = 3T/4 = 3/4 2π/5 = 3π/10 s a = αγων R = 100/3 rad/s2 0,2 m = 20/3 rm/s2
v = a t = 20/3 m/s2 0,3π s = 2π m/s
dK/dt = m2 a v = 2 20/3 2π = 80π/3 J/s
L = m2 v R = 2 2π 0,2 = 0,8π kg m2/s
m2 g - T = m2 a => 20 - T = 2 20/3 => T = 20 - 40/3 = 20/3 N
L = m v R v = ω R v = a t ω = αγων t a = R αγων mg - T = m a dK/dt = m a v
ΟΕΦΕ 2008
ΘΕΜΑ 4ο
O αρχικά ακίνητος τροχός του σχήματος που βρίσκεται στη βάση κεκλιμένου επιπέδου ( θέση Α ) γωνίας κλίσεως 30° αποτελείται από ένα λεπτό ομογενή δακτύλιο μάζας 6kg και ακτίνας 1m και δύο λεπτές ομογενής ράβδους μήκους 2m και μάζας 3kg η κάθε μία που είναι τοποθετημένες κάθετα μεταξύ τους.
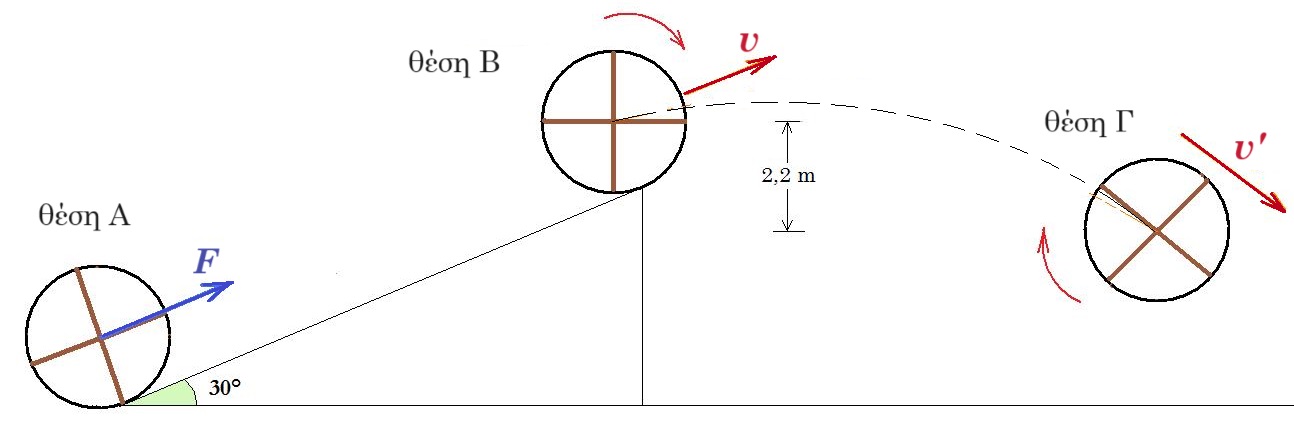 Τη στιγμή t =0 ασκούμε στο κέντρο μάζας Ο του τροχού σταθερή δύναμη F = 100 Ν παράλληλη στο κεκλιμένο επίπεδο και ο τροχός αρχίζει να κυλίεται χωρίς να ολισθαίνει ανερχόμενος στο κεκλιμένο επίπεδο. Όταν ο τροχός φθάσει στην κορυφή του κεκλιμένου επιπέδου ( θέση Β ) έχει εκτελέσει 25/2π περιστροφές. Στη θέση Β καταργούμε την δύναμη F και ο τροχός στη συνέχεια εγκαταλείπει το κεκλιμένο επίπεδο διαγράφοντας καμπύλη τροχιά. Να υπολογίσετε :
Τη στιγμή t =0 ασκούμε στο κέντρο μάζας Ο του τροχού σταθερή δύναμη F = 100 Ν παράλληλη στο κεκλιμένο επίπεδο και ο τροχός αρχίζει να κυλίεται χωρίς να ολισθαίνει ανερχόμενος στο κεκλιμένο επίπεδο. Όταν ο τροχός φθάσει στην κορυφή του κεκλιμένου επιπέδου ( θέση Β ) έχει εκτελέσει 25/2π περιστροφές. Στη θέση Β καταργούμε την δύναμη F και ο τροχός στη συνέχεια εγκαταλείπει το κεκλιμένο επίπεδο διαγράφοντας καμπύλη τροχιά. Να υπολογίσετε :
(α) Το μέτρο της στατικής τριβής που δέχεται που δέχεται ο τροχός από το κεκλιμένο επίπεδο αν ανεβαίνει με γωνιακή επιτάχυνση αγων = 2 rad/s2.
(β) Βρείτε την ταχύτητα του ανώτερου σημείου του τροχού τη στιγμή που αυτός φθάνει στην θέση Β
(γ) Την ταχύτητα του κέντρου μάζας του τροχού τη στιγμή που διέρχεται από τη θέση Γ αν η κατακόρυφη μετατόπιση του κέντρου μάζας του τροχού από τη θέση Β μέχρι τη θέση Γ είναι 2,2 m προς τα κάτω.
(α) R = L/2 = 1m acm = aγων R = 2 rad/s2 1m => acm = 2 m/s2 επιτάχυνση κέντρου μάζας τροχού
F - Mολική g ημ30° - Τ = Mολική αcm => 100 - 12 10 0,5 - Τ = 12 2 => 40 - Τ = 24 => Τ = 16 Ν
(β) θ = Ν 2π => θ = 25/2π 2π = 25 rad s = θ R = 25 m h = s ημ30° = 25 0,5 =12,5 m
s = ½ α t2 => 25 = ½ 2 t2 => t = 5 s vcm = acm t = 2 m/s2 5 s => vcm = 10 m/s
ω = vcm / R = 10 / 1 => ω = 10 rad/s
v2 = vcm2 + (ωR)2 + 2 vcm ωR συν30° = 102 + 102 + 2 10 10 √3/2 = 102 (2 + 2√3) =>
=> v = 10 √(2+2√3) m/s
(γ) το στερεό στον αέρα δεν δέχεται δύναμη που να δημιουργεί ροπή συνεπώς η γωνιακή ταχύτητά του είναι σταθερή ω = 10 rad/s
διατήρηση ενέργειας Mολική g h + ½ Mολική υ2 = ½ Mολική υ'2 => 10 2,2 + ½ 102 = ½ υ'2 =>
=> 22 + 50 = ½ υ'2 => v'2 = 144 => v' = 12 m/s
πλάγια βολή : υ0,x = v0 συν30° = 10 √3/2 = 5√3 m/s ,
υ0,y = v0 ημ30° = 10 0,5 = 5 m/s
x = υ0,x t = v0 συν30° t
y = h = v0 ημ30° t - ½ g t2 => - 2,2 = 10 ½ t - ½ 10 t2 => 5 t2 - 5 t - 2,2 = 0
Δ = 25 + 44 = 69 = 8,32 t = (5 ± 8,3) / 10 = 1,33 sec ή - 0,33 sec
vy = v0,y - g t = v0 ημ30° - g t = 10 ½ - 10 1,33 = 5 - 13,3 => vy = - 8,3 m/s
v2 = vx2 + vy2 = v0,x2 + vy2 = (5√3)2 + (- 8,3)2 = 75 + 69 = 144 => v = 12 m/s
ΟΕΦΕ 2007
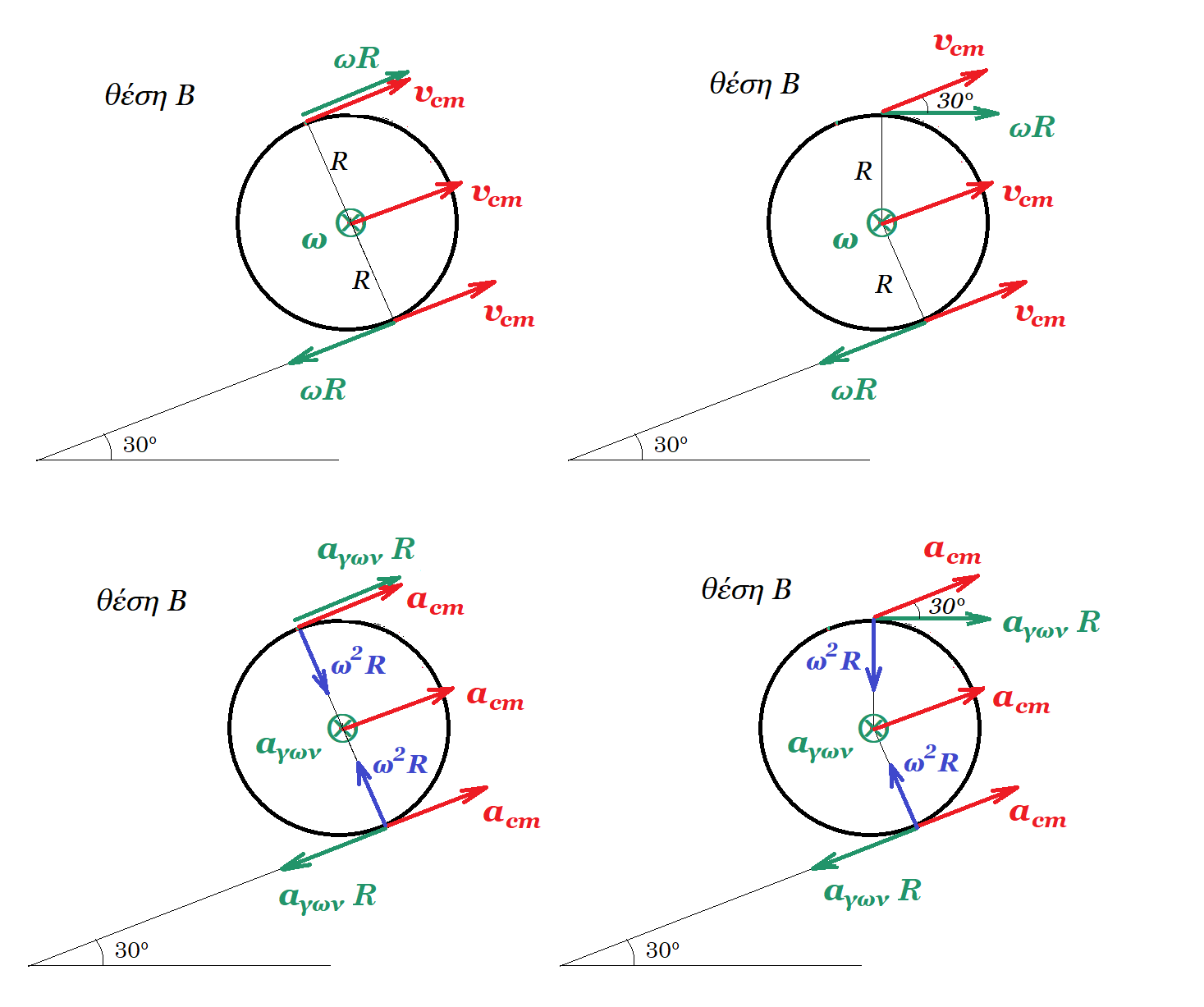
Σώμα Σ1 μάζας m1 = 2 kg μπορεί να κινείται κατακόρυφα προς τα κάτω έτσι ώστε μέσω της τροχαλίας μάζας m = 2 kg να ξετυλίγεται το σχοινί που είναι τυλιγμένο γύρω από τον κύλινδρο ακτίνας R = 0,2 m που μπορεί να περιστρέφεται με τον άξονα του κατακόρυφο. Κατακόρυφη αβαρής ράβδος αμελητέας ακτίνας διέρχεται από τον άξονα του κυλίνδρου και στο επάνω άκρο της στερεώνεται από το μέσο της δεύτερη οριζόντια αβαρής ράβδος μήκους l = 1 m. Δύο μικροί δακτύλιοι Σ2 και Σ3 με αμελητέες διαστάσεις και ίσες μάζες m2 = m3 = 0,025 kg βρίσκονται στα άκρα της οριζόντιας ράβδου και συνδέονται μεταξύ τους μέσω αβαρούς νήματος με όριο θραύσης Τθρ = 25 Ν. Το όλο σύστημα μπορεί να στρέφεται χωρίς τριβές σαν ενιαίο σώμα γύρω από άξονα που έχει τη διεύθυνση της κατακόρυφης ράβδου. Το νήμα που συνδέει τους δακτυλίους και το σχοινί που συνδέει το σώμα Σ1 με τον κύλινδρο παραμένουν διαρκώς τεντωμένα. Η τριβή ανάμεσα στη τροχαλία και το σχοινί είναι αρκετά μεγάλη ώστε να μην παρατηρείται ολίσθηση.
Να βρεθούν :
(α) η τάση του νήματος που ασκείται στο σώμα Σ1 αν η επιτάχυνση του είναι α = 4 m/s2
(β) η συχνότητα περιστροφής των δακτυλίων Σ2 και Σ3 μετά από χρονικό διάστημα 1,5π s από την έναρξή της περιστροφής τους
(γ) η ροπή αδράνειας του κυλίνδρου ως προς τον άξονα περιστροφής του συστήματος
(δ) η γωνία περιστροφής του κυλίνδρου από την έναρξη της περιστροφής του συστήματος μέχρι τη στιγμή που το νήμα που συνδέει τους δακτυλίους είναι έτοιμο να κοπεί.

m1 g - T1 = m1 a => 20 - T1 = 2 a (1) a = 4 m/s2 τότε T1 = 12 N
( T1 - T2 ) R1 = I(τροχ) aγων,1 => ( T1 - T2 ) R1 = ½ m R12 aγων,1 => T1 - T2 = ½ 2 R1 aγων,1
=> T1 - T2 = R1 aγων,1 = a (2) τότε Τ2 = Τ1 - α = 12 - 4 = 8 Ν
a = R1 aγων,1 = R aγων,2 => aγων,2 = α / R = 4 / 0,2 = 20 rad/s2 γωνιακή επιτάχυνση κυλίνδρου
τότε ωκυλίνδρου = aγων,2 t = 20 1,5 π => ωκυλίνδρου = 30 π rad/s f = ωκυλίνδρου / 2π = 15 Ηz
T2 R = I aγων,2 => T2 0,2 = [ m2 (L/2)2 + m3 (L/2)2 + Ι(Κ) ] aγων,2 =>
=> T2 0,2 = [ 2 0,025 0,52 + Ι(Κ) ] 20 => 8 = [ 0,0125 + Ι(Κ) ] 100 => 8 = 1,25 + Ι(Κ) 100 => Ι(Κ) = 0,0675 kg m2
Tθραύσεως = Fκεντρομόλος = m2 ω2 L/2 => 25 = 0,025 ω2 1/2 => ω2 = 2000 = ( 20 t )2 => t2 = 2000 / 400 = 5 => t = 5½ s τότε θ = ½ aγων,2 t2 = ½ 20 5 => θ = 50 rad
ΟΕΦΕ 2006
H ομογενής ράβδος ΟΑ του σχήματος έχει μήκος L = 1 m μάζα m = 3 kg και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο χωρίς τριβές γύρω από οριζόντιο ακλόνητο άξονα που περνά από το άκρο της Ο και είναι κάθετος σε αυτή.
Α. Η ράβδος ισορροπεί σε οριζόντια θέση με τη βοήθεια δύναμης F1 που ασκείται στο άκρο Α κάθετα στη ράβδο.
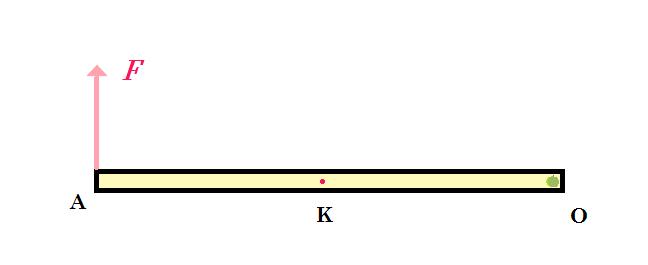
Να υπολογίσετε το μέτρο της F1 και το μέτρο της δύναμης που δέχεται η ράβδος από τον άξονα περιστροφής.
Β. Ασκώντας στο άκρο Α αντί της δύναμης F1 άλλη δύναμη F2 σταθερού μέτρου 60/π Ν διαρκώς κάθετη στη ράβδο, η ράβδος ανέρχεται και περνά από την ανώτερη θέση της με γωνιακή ταχύτητα ω0 = √30 rad/s. Τη στιγμή αυτή η F2 παύει να ασκείται στη ράβδο. Υπολογίστε την κινητική ενέργεια της ράβδου.
Γ. Τη στιγμή κατά την οποία η ράβδος διέρχεται από την οριζόντια θέση στη διάρκεια της καθόδου της να υπολογίσετε :
(α) το ρυθμό μεταβολής της στροφορμής της ράβδου ως προς τον άξονα περιστροφής της.
(β) το ρυθμό μεταβολής της κινητικής ενέργειας της ράβδου.
Δ. Σημειακή μάζα m1 = 0,1 kg κινούμενη οριζόντια με ταχύτητα μέτρου υ1 = 100 m/s συγκρούεται πλαστικά με την ράβδο τη στιγμή που διέρχεται από το κατώτερο σημείο της τροχιάς της. Πόσο πρέπει να απέχει το σημείο σύγκρουσης από τον άξονα περιστροφής της ράβδου ώστε αυτή να ακινητοποιηθεί μετά την σύγκρουση;
(Α) ροπές ως προς Ο : m g L/2 = F1 L => F1 = m g /2 = 3 10 / 2 = 15 N
ΣF = 0 => m g - F1 + F(O) = 0 => 30 - 15 + F(O) = 0 => F(O) = - 15 N
κατεύθυνση κατακόρυφη προς τα πάνω με μέτρο 15 Ν
(Β) έργο της F2 : WF2 = F2 π/2 L = 60/π π/2 1 = 30 J
U = m g L/2 = 3 10 0,5 = 15 J άρα η κινητική ενέργεια της ράβδου είναι Κ = WF2 - U = 15 J
(Γ) Στ(Ο) = Ι(Ο) αγων => m g L/2 = 1/3 m L2 αγων => 15 rad/s2 = αγων
½ I(Ο) ω0 2 + m g L/2 = ½ I(Ο) ω1 2 => ½ 1/3 m L2 ω0 2 + m g L/2 = ½ 1/3 m L2 ω1 2 => ω1 2 = ω0 2 + 3g/L = 30 + 30 = 60 => ω1 = 60½ rad/s
dK/dt = I(Ο) ω1 αγων = 1/3 m L2 ω1 αγων = 1/3 3 12 60½ 15 = 15 60½ J/s
(Δ) ½ I(Ο) ω1 2 + m g L/2 = ½ I(Ο) ω2 2 => ½ 1/3 m L2 ω1 2 + m g L/2 = ½ 1/3 m L2 ω2 2 => ω2 2 = ω1 2 + 3g/L = 60 + 30 = 90 => ω2 = 90½ rad/s
m1 v1 r - I(Ο) ω2 = 0 => 0,1 100 r - 1 90½ = 0 => r = 90½ /10 m
ΟΕΦΕ 2004
H τροχαλία του σχήματος είναι ομογενής μάζας Μ = 4 kg και ακτίνας R = 0,2 m. Τα σώματα Σ1 και Σ2 έχουν μάζες m1 = 4 kg και m2 = 2 kg και το σχοινί που τα συγκρατεί έχει αμελητέα μάζα. Το σώμα Σ2 είναι κολλημένο με άλλο σώμα Σ3 μάζας m3 = 1 kg. Το σώμα Σ3 είναι στερεωμένο στο άκρο κατακόρυφου ελατηρίου σταθεράς k = 100 N/m το άλλο άκρο του οποίου είναι στερεωμένο στο έδαφος. Το σύστημα αρχικά ισορροπεί ακίνητο. Τη στιγμή t = 0 τα σώματα Σ1 και Σ2 αποκολλούνται.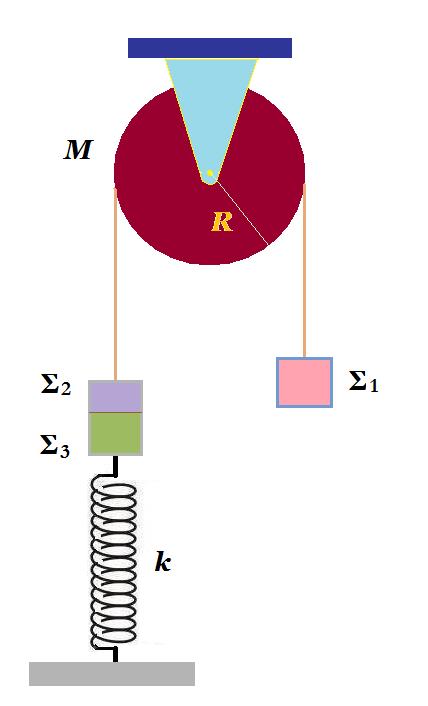
(α) Γράψτε την εξίσωση της απομάκρυσης της ταλάντωσης που θα εκτελέσει το σώμα Σ3 .
(β) Αν η γωνιακή ταχύτητα της τροχαλίας τη στιγμή που το σώμα Σ3 διέρχεται από τη θέση ισορροπίας του για πρώτη φορά είναι 5π/8 rad/s υπολογίστε την τάση του νήματος στα δύο άκρα του.
(γ) Υπολογίστε την συνολική στροφορμή των σωμάτων Σ1 και Σ2 τη στιγμή t = 2 s.
H τριβή ανάμεσα στην τροαλία και το σχοινί είναι αρκετά μεγάλη ώστε δεν παρατηρείται ολίσθηση. Τα σώματα Σ1 , Σ2 και Σ3 είναι μικρών διαστάσεων.
(α) ισορροπία Σ1 : m1 g = T => 4 10 = T => T = 40 N
ισορροπία Σ2,3 : ( m2 + m3 ) g + Fελατ = T => ( 2 + 1 ) 10 + Fελατ = 40 => Fελατ = 10 Ν => Fελατ = k Δl => Δl = 10 / 100 = 0,1 m επιμήκυνση
τα σώματα Σ2 και Σ3 αποκολλούνται :
ισορροπία Σ3 : m3 g = k x3 => x3 = m3 g / k = 1 10 / 100 => x3 = 0,1 m συσπείρωση
πλάτος ταλάντωσης Σ3 : Α = Δl + x3 = 0,1 m + 0,1 m = 0,2 m
ω2 = k / m3 = 100 / 1 => ω = 10 rad/s x(t) = 0,2 ημ(10t + π/2)
υ(t) = 2 συν(10t + π/2) α(t) = - 20 ημ(10t + π/2) ΣF(t) = m3 a(t) = - 20 ημ(10t + π/2)
(β) t = T/4 = 2π / 40 s = π/20 s επειδή m1 > m2 το Σ1 κατέρχεται το Σ2 ανέρχεται και η τροχαλία στρέφεται δεξιόστροφα
ω = aγων t => 5π/8 rad/s = αγων π/20 s => αγων = 12,5 rad/s2
α = aγων R = 12,5 / 0,2 => a = 2,5 m/s2
m1 g - T1 = m1 α => 4 10 - T1 = 4 2,5 => 40 - T1 = 10 => T1 = 30 N
T2 - m2 g = m2 α => T2 - 2 10 = 2 2,5 => T2 - 20 = 5 => T2 = 25 N
(γ) v = a t = 2,5 m/s2 2 s = 5 m/s
L1 = m1 v R = 4 kg 5 m/s 0,2 m = 4 kg m2 / s δεξιόστροφη
L2 = m2 v R = 2 kg 5 m/s 0,2 m = 2 kg m2 / s δεξιόστροφη
L1,2 = L1 + L2 = 6 kg m2 / s δεξιόστροφη