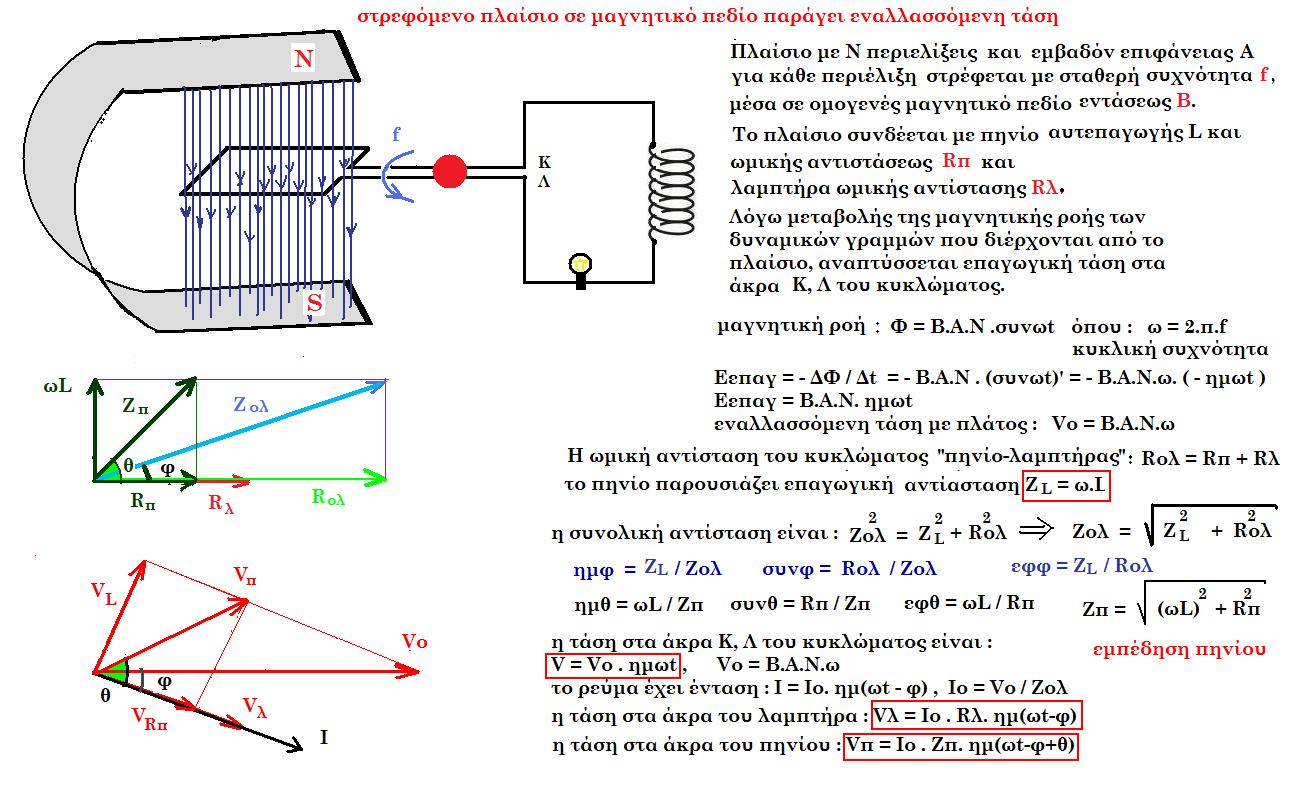
V = Vo . ημωt            V = i . (Rπ + Rλ)  + L.di/dt  = Vo . ημωt     (1)

i = Io . ημ(ωt + φ)     di/dt = ω.Ιο. συν(ωt + φ)         Rολ = Rπ  + Rλ  

(1) =>  Ιο . ημ(ωt + φ) . (Rπ + Rλ )  +  L . ω.Ιο. συν(ωt + φ)  = Vo . ημωt  =

= Io . (Rπ + Rλ) . (ημωt. συνφ + συνωt .ημφ) +  ω.L.Io . (συνωt .συνφ - ημωt. ημφ) 

εξισώνουμε  τους  συντελεστές ως προς  ημωt   και συνωt     

ημ :     Ιο. Rολ .συνφ  -  ω.L.Io . ημφ  =  Vo    (2)

συν :   Ιο. Rολ .ημφ  +  ω.L.Io .συνφ  =  0    =>    εφφ  =  - ω.L / Rολ  - 90° < φ < 0°   

                                       ημφ = - ω.L / Zολ     συνφ = Rολ / Ζολ            Ζολ2 =  (ω.L)2  +  ( Rπ + Rλ )2   

(2) =>    Ιο . Rολ . Rολ / Ζολ  -  ω.L. Io . ( - ω.L / Ζολ )  =  Vo    =>

     =>     Io . [ Rολ2  +  (ω.L)2 ]   =  Zολ . Vo    =>    Io . Zολ = Vo   

η τάση στα άκρα του λαμπτήρα είναι :    Vλ  = i . Rλ  =  Ι0 . Rλ . ημ(ωt + φ) 

η τάση στα άκρα του πηνίου είναι :     Vπ  =  L . di/dt  +  i . Rπ  =  L.ω. Ιο . συν(ωt + φ)  +  Ιο . ημ(ωt + φ) . Rπ   =  

                                                                          = A . ημ(ωt + φ + θ)   =   Α . ημ(ωt + φ) .συνθ  +  Α . συν(ωt +φ) . ημθ

     συνεπώς : Α . συνθ = Ιο . Rπ     και      Α . ημθ = Ιο . ωL     προκύπτει :  εφθ = ωL/Rπ   και

                      (Α.ημθ)2 + (Α.συνθ)2 = Ιο2 . [ (ωL)2 + Rπ2 ]   =>    Α2 = Ιο2 . [ (ωL)2  + Rπ2 ]   =   Ιο2 . Ζπ2

τελικά :    Vπ = Ι0 . Ζπ . ημ(ωt + φ + θ)       ημθ = ω.L / Zπ ,   συνθ = Rπ / Ζπ ,  εφθ = ω.L / Rπ  ,   Ζπ2 = (ω.L)2 + Rπ2    συνολική εμπέδηση πηνίου

 

το πλάτος της τάσης στα άκρα του λαμπτήρα είναι :  V0,λ =  Ι0 . Rλ  =  V0 / Zολ . Rλ  =  V0 . Rλ /  [ (ωL)2 + (Rπ + Rλ )2 ]½    

αν η συχνότητα  ω  είναι πολύ μικρή   ( ω --> 0 )   τότε  :   V0,λ = V0 . Rλ  /  (Rπ + Rλ)

αν η συχνότητα ω είναι πάρα πολύ μεγάλη  ( ω --> + οο )  τότε :  V0,λ =  0     διότι  ωL --> + οο. 

     η συνάρτηση   g(ω) = Rλ / [ (ωL)2 + (Rπ + Rλ)2 ]1/2    είναι  φθίνουσα  διότι   g' (ω) < 0 ,  ω > 0

                                                                           g' (ω) =  - Rλ.ω.L2 / [ (ωL)2 + (Rπ + Rλ)2 ]3/2   <  0

 

το πλάτος της τάσης στα άκρα του πηνίου είναι :   V0,π = Ι0 . Ζπ =  V0 / Zολ . Ζπ  =  V0 . [ (ωL)2 + Rπ2 ]½  /  [ (ωL)2 + (Rπ + Rλ)2 ]½  

αν η συχνότητα  ω  είναι πολύ μικρή  ( ω --> 0 )   τότε :    V0,π = V0 . Rπ / ( Rπ + Rλ )   

αν η συχνότητα  ω  είναι πολύ μεγάλη  ( ω --> + οο )  έχουμε :  Ζπ --> ωL  και  Ζολ  -->  ωL    οπότε :  V0,π  -->  V0 . ωL / ωL  =  V0    

     η συνάρτηση  ψ(ω) =  [ (ωL)2 + Rπ2 ]½ / [ (ωL)2 + (Rπ + Rλ)2 ]½   είναι  αύξουσα διότι  ψ' (ω) > 0 , ω > 0      

                          ψ' (ω) =  ω.L2 . [ (Rπ + Rλ)2 - Rπ2 ] . [ (ωL)2 + Rπ2 ]-1/2  . [ (ωL)2 + (Rπ + Rλ)2 ]-3/2    >  0