ΘΕΜΑ 4ο      τροποποίηση
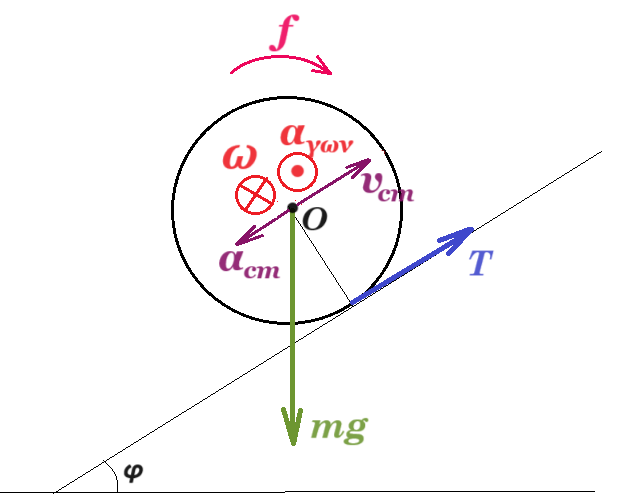
Συμπαγής και ομογενής σφαίρα μάζας m=10 kg και ακτίνας R=0,1 m κυλίεται ευθύγραμμα χωρίς ολίσθηση ανερχόμενη κατά μήκος κεκλιμένου επιπέδου γωνίας φ με ημφ=0,56. Τη χρονική στιγμή t=0 το κέντρο μάζας της σφαίρας έχει ταχύτητα με μέτρο υ₀=8m/s. Να υπολογίσετε για τη σφαίρα:

α.  το μέτρο της γωνιακής ταχύτητας περιστροφής της τη χρονική στιγμή t=0.        Μονάδες 6
β.  αν το μέτρο του ρυθμού μεταβολής της στροφορμής κατά τη διάρκεια της κίνησής της είναι 1,6 Ν⋅m,  δηλαδή η συνισταμένη ροπή ως προς το κέντρο μάζας Ο της σφαίρας, να υπολογίσετε την επιτάχυνση του κέντρου μάζας Ο της σφαίρας και την γωνιακή επιτάχυνσή της.             Μονάδες 10
γ.  το μέτρο της ταχύτητας του κέντρου μάζας της καθώς ανεβαίνει, τη στιγμή που έχει διαγράψει 30/π  περιστροφές.

Μονάδες 9

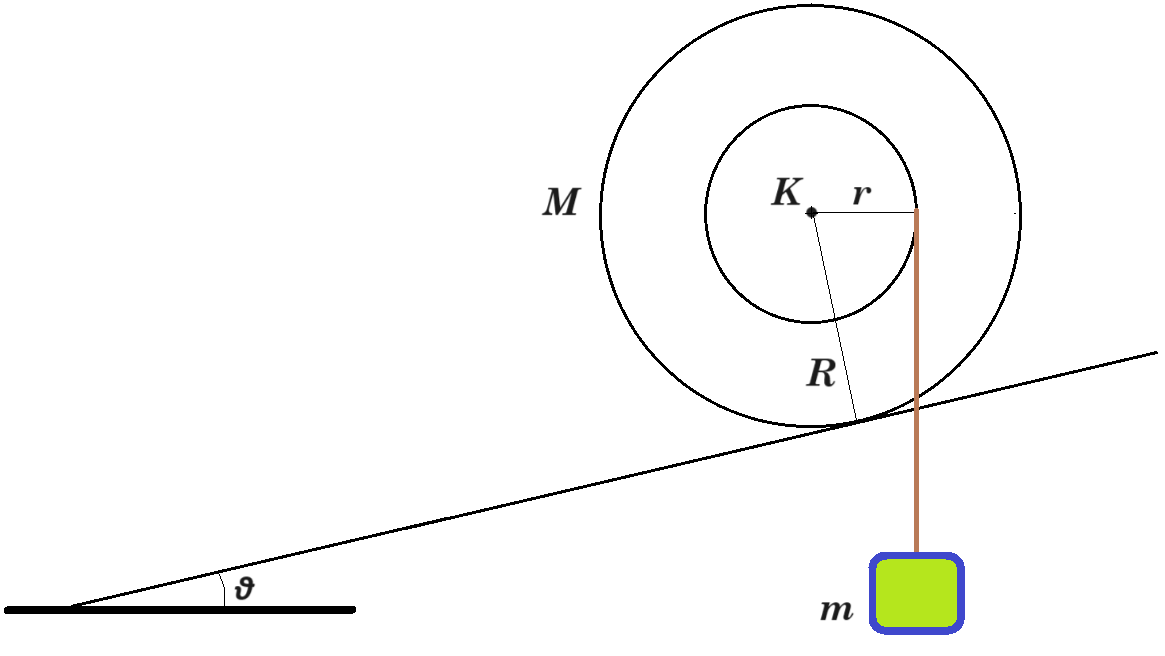
Ομογενής τροχαλία μάζας Μ και αμελητέου πάχους αποτελείται από δύο συγκολλημένους δίσκους με ακτίνες r και R, όπου R =2r. Ο μικρότερος δίσκος ακτίνας r φέρει ένα αυλάκι στην περιφέρειά του γύρω από το οποίο είναι τυλιγμένο πολλές φορές λεπτό, αβαρές και μη εκτατό νήμα, στο ελεύθερο άκρο του οποίου είναι δεμένο βαρύδι μάζας m. Η τροχαλία ακουμπά στην επιφάνεια κεκλιμένου επιπέδου γωνίας κλίσης θ, όπου ημθ=1/10.Αν όλη η διάταξη ισορροπεί στατικά και οριακά μέσα σε βαρυτικό πεδίο έντασης μέτρου g, στο οποίο η αντίσταση του αέρα είναι αμελητέα, τότε

1)  ο συντελεστής της μέγιστης στατικής (οριακής) τριβής  μ_σ  μεταξύ τροχαλίας και επιπέδου είναι ίσος με:

i)  σφθ          ii)  εφθ           iii)  συνθ

2)  ο λόγος των μαζών του βαρυδίου προς της τροχαλίας m/M ισούται με

i)  1/6           ii)  1/4            iii)  1/2

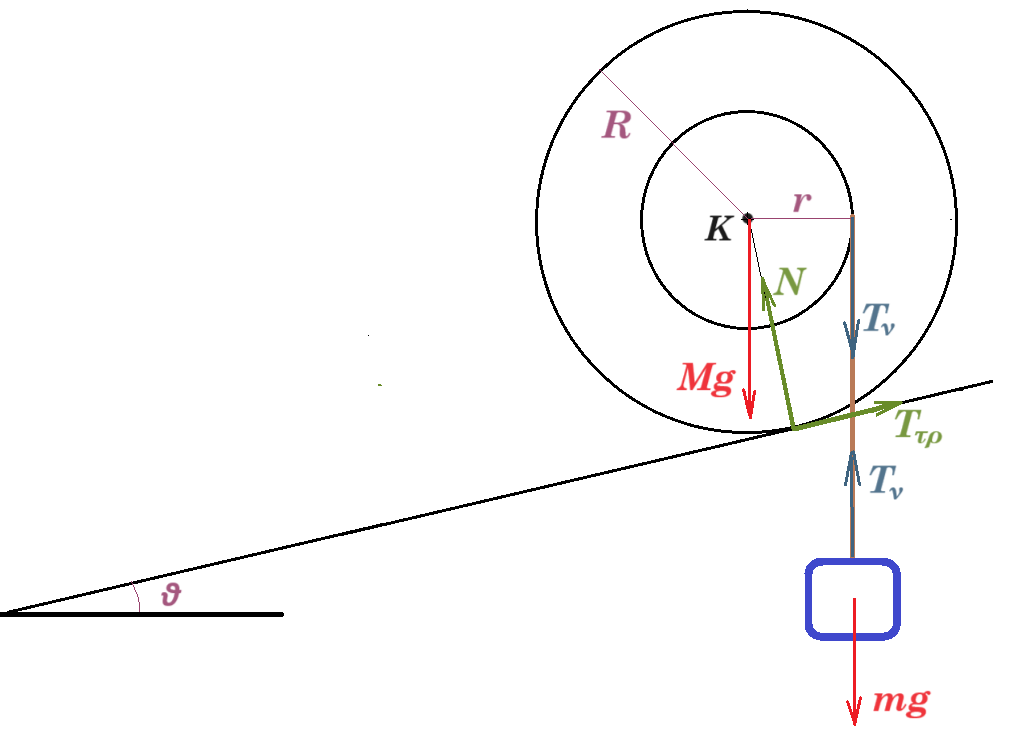       ισορροπία σώματος :   mg = T_ν       

  ισορροπία τροχού :  Στ_(Κ) = 0  =>  Τ_τρ R = Τ_ν r  =>  Τ_τρ R =  Τ_ν R/2  =>  Τ_τρ = Τ_ν / 2  = mg / 2       

ΣF_x = 0  =>  Τ_τρ  -  Mg ημθ  -  Τ_ν ημθ  =  0   =>  mg / 2  -  Mg  1/10  -  mg  1/10  =  0  =>  M = 4m

ΣF_y = 0  =>  N  -  Mg συνθ  -  Τ_ν συνθ  =  0  =>  N  -  4mg συνθ  -  mg συνθ  =  0 =>  N = 5mg συνθ

  μ_σ  =  Τ_τρ / Ν =   1/2 mg  /  5 mg συνθ  =  1 / 10συνθ  =  1/10 / συνθ  =  ημθ / συνθ  =>  μ_σ = εφθ

α)      v_cm  =  v₀ = ω₀⋅R  =>  8 m/s = ω₀ ⋅ 0,1 m  =>  ω₀ = 80 rad/s 

β)    dL/dt = Στ_(Ο) = Τ⋅R   =>  1,6 Ν⋅m =  Τ⋅ 0,1 m  =>  Τ = 16 Ν

   ΣF = m a_cm  =>   T  -  mg ημφ =  m a_cm  =>   16  -  10 10 0,56  =  10 a_cm  => 16 -  56  =  10 a_cm  =>  a_cm = - 4 m/s²  

         α_γων = a_cm / R = - 4 m/s² / 0,1 m => α_γων = - 40 rad/s²    

γ)      N = 30/π στροφές  =>  θ = Ν 2π = 30/π  2π = 60 rad     

  θ = ω₀ t +  ½ α_γων t²  =>  60 = 80 t -  ½ 40 t²  =>   t² - 4 t + 3 = 0   =>  (t - 3) (t - 1) = 0  =>    t = 1 s   ή   t = 3 s   

  t = 1 s     ω = ω₀ + α_γων t  =  80  -  40  =  40 rad/s     v_cm = ω⋅R =  40  0,1 = +4 m/s    η σφαίρα ανέρχεται στο κεκλιμένο

  t = 3 s     ω = ω₀ + α_γων t  =  80  -  40⋅3  =  - 40 rad/s     v_cm = ω⋅R = - 40  0,1 = - 4 m/s     η σφαίρα κατέρχεται στο κεκλιμένο