1ο ΘΕΜΑ
Στο bungee jumping ο αθλητής ή η αθλήτρια πραγματοποιούν άλμα από μία πλατφόρμα, αμελητέου πάχους, που έχει τοποθετηθεί πάνω από μία λίμνη, ένα ποτάμι ή την θάλασσα.
Στα πόδια τους προσδένεται η άκρη ελαστικού νήματος, η άλλη άκρη του οποίου στερεώνεται ακλόνητα στην πλατφόρμα. Η συμπεριφορά του νήματος περιγράφεται με καλή προσέγγιση από το Νόμο του Hooke, ενώ η μάζα του θεωρείται αμελητέα.
Φτάνοντας στην ελεύθερη επιφάνεια του νερού, ο άνθρωπος πρέπει να έχει μηδενική ταχύτητα και επιτάχυνση μέτρου 𝛼 = 2𝑔.
Ένας αθλητής μάζας 𝑚 = 70 𝑘𝑔 χρησιμοποιεί ελαστικό νήμα φυσικού μήκους 𝐿, το οποίο είναι πολύ μεγαλύτερο από το ύψος του και αφήνει το σώμα του να πέσει (δηλαδή έχει μηδενική αρχική ταχύτητα) από την πλατφόρμα, η οποία απέχει 90𝑚 από την ελεύθερη επιφάνεια του νερού. Θεωρώντας ότι ο αθλητής ξεκινά την στιγμή 𝑡𝑜 = 0, ότι στον τόπο όπου πραγματοποιείται το άλμα και για όλο το διανυόμενο ύψος, η επιτάχυνση της βαρύτητας έχει σταθερή τιμή 𝑔 = 10 𝑚/𝑠2 και ότι η αντίσταση του αέρα είναι αμελητέα, να:
Α.1. αποδείξετε ότι το νήμα που θα χρησιμοποιηθεί πρέπει να έχει φυσικό μήκος 𝐿 = 30𝑚
και σταθερά ελαστικότητας 𝑘 = 35 𝑁/𝑚,
Α.2. υπολογίσετε το μήκος 𝐿1 του νήματος στην θέση ισορροπίας του ανθρώπου,
Α.3. υπολογίσετε την μέγιστη ταχύτητα 𝜐𝑚𝑎𝑥 που αναπτύσσει ο άνθρωπος στην διάρκεια του άλματος.
Α.4. υπολογίσετε την χρονική στιγμή 𝑡1 που φθάνει στην επιφάνεια του νερού για πρώτη φορά, αν γνωρίζουμε ότι το χρονικό διάστημα για να πάει ένα σώμα που ταλαντώνεται, από τη θέση ισορροπίας του στη θέση x = ±A/2 είναι Τ/12.
2ο ΘΕΜΑ
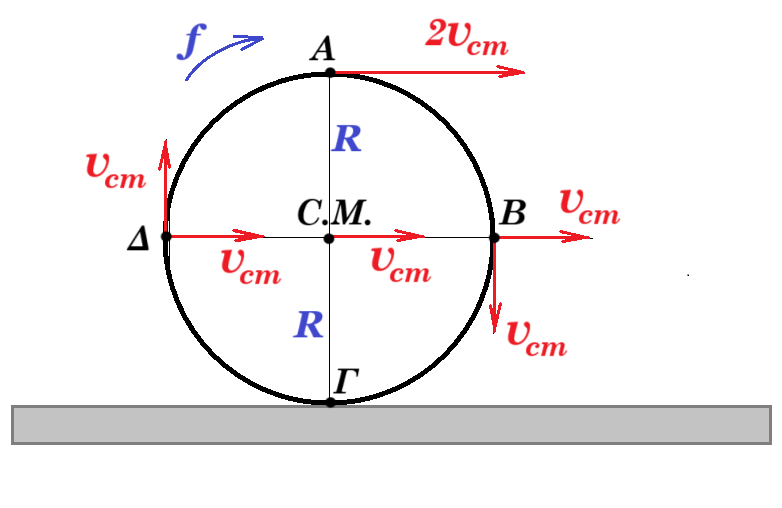
Τροχός ακτίνας 𝑅 = 1𝑚 κινείται σε οριζόντιο λασπωμένο έδαφος εκτελώντας κύλιση χωρίς ολίσθηση με σταθερή ταχύτητα 𝜐𝑐𝑚 = √10 𝑚/s. Κάποια χρονική στιγμή, έστω 𝑡0 = 0, αποκολλώνται από τα σημεία Α, Β και Δ της περιφέρειάς του τρία μικρά κομμάτια λάσπης.
Βρείτε τις ταχύτητες των κομματιών λάσπης όταν αυτά φθάνουν στο έδαφος και μετά για κάθε ένα βρείτε την μεταβολή της ορμής του.
Να συγκρίνεται τους χρόνους πτώσεως των κομματιών.
Θεωρώντας την αφετηρία του συστήματος αναφοράς στο σημείο Γ του σχήματος, βρείτε τις θέσεις 𝑥𝛢, 𝑥𝛣 και 𝑥𝛥 καθώς και την θέση 𝑥𝑐𝑚 την χρονική στιγμή 𝑡𝐴 όπου το κομμάτι από το σημείο Α φτάνει στο έδαφος.
1ο ΘΕΜΑ
a = 2g = ω2Α => 20 = k/m A => 20 = k/70 A => k A = 1400 (1)
ισορροπία σώματος : m g = k x0 = 700 (2)
διατήρηση ενέργειας : ½ k (x0 + A)2 = m g h => k (x0 + A)2 = 2 70 10 90 (3)
(1) / (2) => A = 2 x0 (4)
(3) , (4) => k (3x0)2 = 2 70 10 90 => k 9 x02 = 2 70 10 90 => k x02 = 14000 (5)
(5) / (2) => x0 = 20 m επιμήκυνση ελαστικού νήματος όταν ο αθλητής ισορροπεί
πλάτος ταλάντωσης : (4) => Α = 40 m
90 m = L + x0 + A = L + 20m + 40m = L + 60m => L = 30 m
L1 = x0 + L = 20m + 30m => L1 = 50 m
σταθερά ελαστικότητας : (2) => k 20 = 700 => k = 35 N/m
ω2 = k/m = 35 / 70 = 1/2 ω = 1/√2 rad/s T = 2π/ω = π.2√2 s
vmax = ω Α = 1/√2 40 => vmax = 20√2 m/s
κατ' αρχήν ελεύθερη πτώση : 30 m = 0,5 10 m/s2 t2 => t = √6 s
t1 = √6 s + T/12 + T/4 = √6 s + π.2√2/12 s + π.2√2/4 s = √6 s + π.√2/6 s + π.√2/2 s = √6 s + π.2√2/3 s
2ο ΘΕΜΑ
διατήρηση ενέργειας :
½ m vA2 + m g 2R = ½ m (vA')2 => (2vcm)2 + 4gR = (vA')2 => vA' = 2 ( vcm2 + gR )½
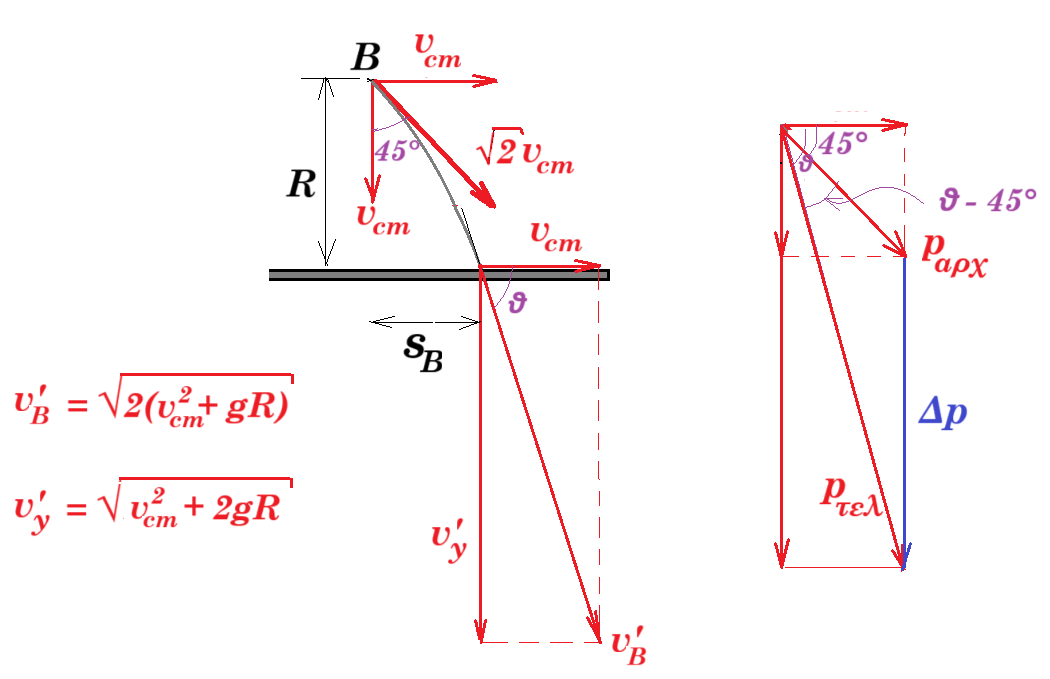
½ m vB2 + m g R = ½ m (vB')2 => (√2 vcm)2 + 2gR = (vB')2 => vB' = √2 ( vcm2 + gR )½
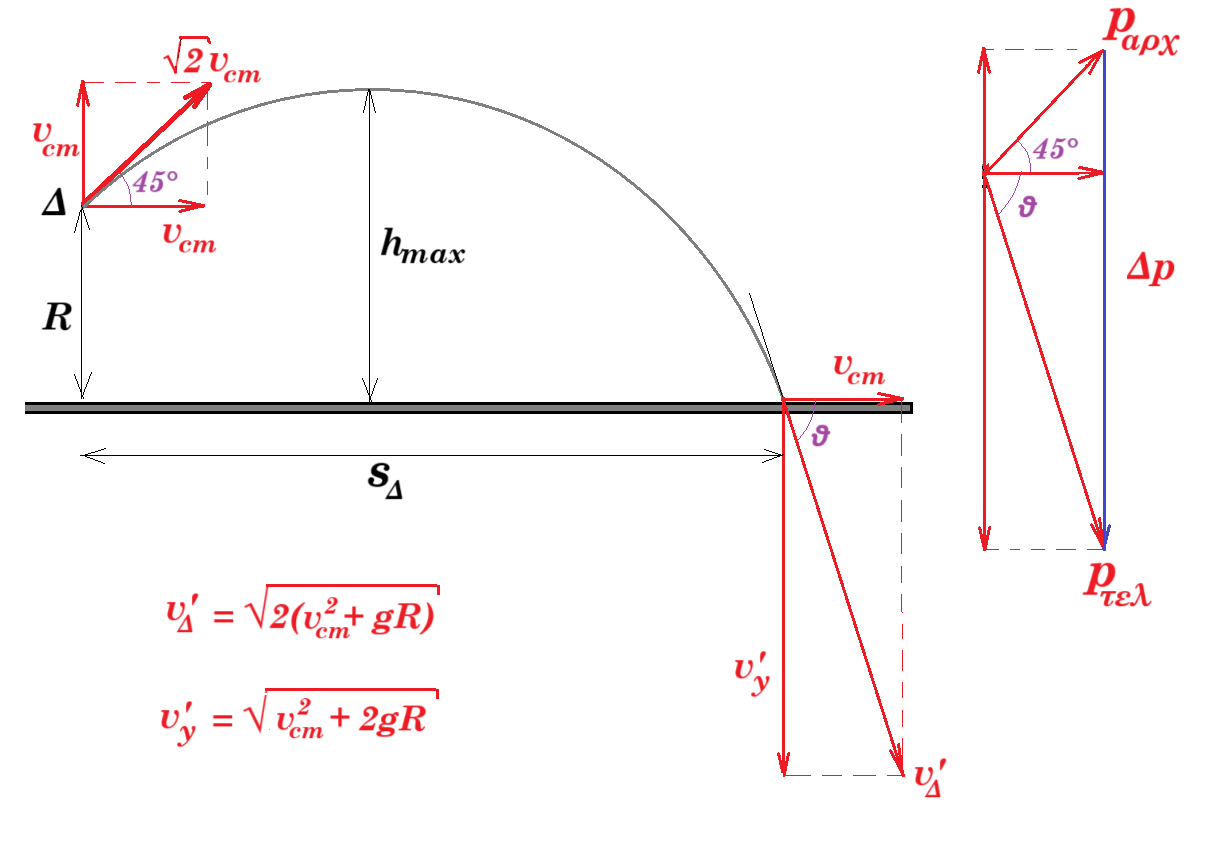
½ m vΔ2 + m g R = ½ m (vΔ')2 => (√2 vcm)2 + 2gR = (vB')2 => vΔ' = √2 ( vcm2 + gR )½
2R = h = ½ g tA2 => tA = 2√(R/g) = 2/√10
θετική προς τα πάνω - R = vcm tΔ - ½ g tΔ2 => g/2 tΔ2 - vcm tΔ - R = 0
Δ = vcm2 + 2gR tΔ = [ + vcm + (vcm2 + 2gR)½ ] / g
θετική προς τα κάτω R = vcm tΒ + ½ g tΒ2 => g/2 tB2 + vcm tB - R = 0
Δ = vcm2 + 2gR tΒ = [ - vcm + (vcm2 + 2gR)½ ] / g
tΒ < tΑ < tΔ
𝑥𝛢 = tA 2vcm = 2/√10 2 √10 = 4 m yΑ = 0,5 g tA2 = 0,5 10 4/10 = 2 m
έχει φθάσει στο έδαφος 4 μέτρα δεξιά
yB = vcm tA + 0,5 g tA2 = √10 2/√10 + 0,5 10 4/10 = 2 + 2 = 4 m είχε πέσει στο έδαφος προηγουμένως
𝑥B = R + tΔ vcm = 1 + [ - vcm + (vcm2 + 2gR)½ ] / g √10 = 1 + [ - √10 + (10 + 20)½ ] / g √10 = 1 + [ - √10 + √30 ] / √10 = 1 - 1 + √3 = √3 m
𝑥Δ = - R + tA vcm = - 1 + 2/√10 √10 = - 1 + 2 = 1 m
yΔ = vcm tA - 0,5 g tA2 = √10 2/√10 - 0,5 10 4/10 = 0 είναι στο ύψος του κέντρου μάζας του τροχού 1 μέτρα δεξιά
𝑥𝑐𝑚 = tA vcm = 2/√10 √10 = 2 m