1.   Μια ομογενής ράβδος μήκους ℓ = 2 m και μάζας Μ = 5 kg ισορροπεί σε οριζόντια θέση στηριγμένη σε δύο στηρίγματα που απέχουν d = 0,5 m από κάθε άκρο της ράβδου. Στο ένα άκρο της ράβδου κρέμεται μέσω ελατηρίου σταθεράς k = 80 N/m σώμα Σ μάζας m = 3,2 kg.
α)    Να βρείτε τη δύναμη που ασκεί κάθε στήριγμα στη ράβδο όταν το σώμα Σ ισορροπεί.
β )   Απομακρύνουμε το σώμα Σ προς τα κάτω κατά Α και το αφήνουμε ελεύθερο να κινηθεί τη χρονική στιγμή t = 0. Να βρείτε τη μέγιστη τιμή του Α για να μην ανατραπεί η ράβδος.
γ)    Για την τιμή του Α που βρήκατε στο (β) ερώτημα:
(i)   Να βρείτε τις εξισώσεις της απομάκρυνσης σαν συνάρτηση του χρόνου για το σώμα Σ, καθώς και της δύναμης του ελατηρίου που ασκείται στη ράβδο σαν συνάρτηση του χρόνου.
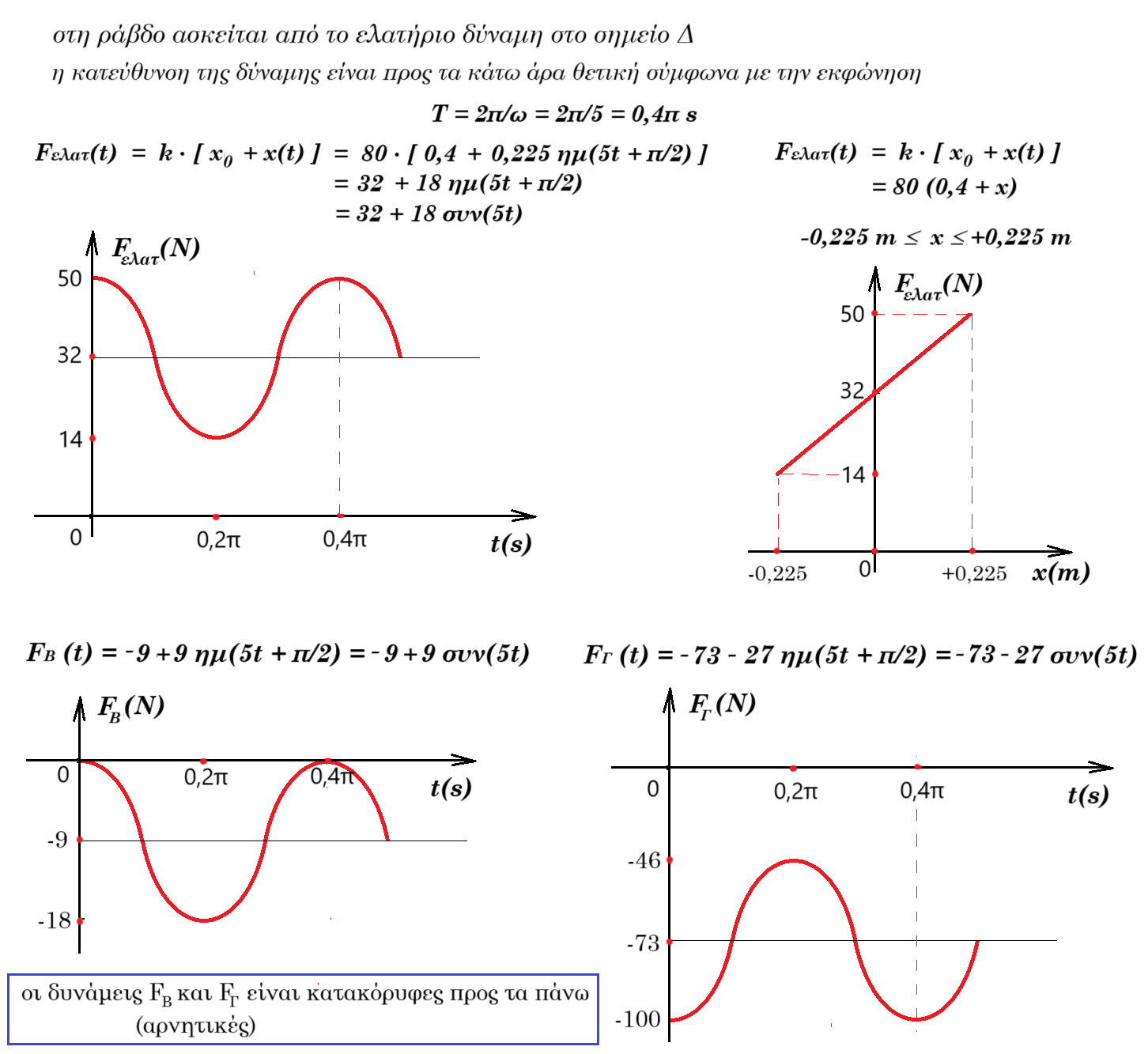
(ii)  Να βρείτε τις εξισώσεις της αντίδρασης κάθε στηρίγματος σαν συνάρτηση του χρόνου και να τις παραστήσετε γραφικά σε βαθμολογημένους άξονες.
 Να θεωρήσετε θετική φορά προς τα κάτω και g =10 m/s² .
[ α) 73 N, 9 N β) 0,225 m γ) (i) x=0,225ημ(5t+π/2), F =32+18ημ(5t+π/2) ΕΛ  (ii) F =73+27ημ(5t+π/2), F =9-9ημ(5t+π/2) ] 

(Α)     ισορροπία  Σ :    m g  =  k x₀  =>   32 = 80 x₀    =>    x₀  =  0,4 m

ροπές ως προς Β :   Mg (L/2 - d)  +  k x₀ (L - d)  =  F_Γ (L - 2d)  =>  5  10  (1 - 0,5)  +  32  (2 - 0,5)  =  F_Γ (2 - 1)   =>  25  +  48  =  F_Γ  =>  F_Γ  =  73 Ν    κατακόρυφη προς τα πάνω

ροπές ως προς Γ :   Mg  (L/2 - d)  =  k x₀ d  +  F_Β  (L - 2d)  =>  5  10  (1 - 0,5)  =  32  0,5  +  F_Β (2 - 1)   =>  25  =  16  +  F_Β   =>   F_Β  =  9 Ν    κατακόρυφη προς τα πάνω

(Β)   ανατροπή ράβδου θα συμβεί όταν  F_Β =  0   τότε το ελατήριο είναι επιμηκυμένο κατά  x₁    

ροπές ως προς Γ :   Mg  (L/2 - d)  =  k x₁ d  +  F_Β (L - 2d)  =>  Mg  (L/2 - d)  =  k x₁ d  =>  50  0,5  = 80  x₁  0,5   =>  x₁ = 0,625 m       συνεπώς απομακρύναμε το σώμα Σ  προς τα κάτω κατά   Α  = x₁ - x₀  =  0,625 - 0,4  =  0,225 m

το σώμα Σ  ταλαντώνεται με πλάτος  Α = 0,225 m  και  κυκλική συχνότητα  ω :    k  =  m ω²  =>  80  =  3,2  ω²  =>   ω²  =  25  =>   ω  =  5 rad/s   

    x(t)  =   0,225 συν5t   =  0,225 ημ(5t + π/2)           υ(t)  =  1,125 συν(5t + π/2)    

    α(t)  =  - 5,625 ημ(5t + π/2)                 F(t)  =  m a(t)  =  3,2  [ - 5,625 ημ(5t + π/2) ]  =  - 18 ημ(5t + π/2)  

  για τη δύναμη ελατηρίου μετράμε από το φυσικό μήκος του ελατηρίου :   F_ελατ(t)  = - k [ x₀ + x(t) ] = - 80 [ 0,4 + 0,225 ημ(5t + π/2) ] = - 32 - 18 ημ(5t + π/2)   

 ενώ  για τη ράβδο στο άκρο της Δ :   F'_ελατ(t) = 32 + 18 ημ(5t + π/2)

(Γ)   ροπές ως προς Β :   Mg (L/2 - d) +  F_ελατ (L - d)  =  F_Γ  (L - 2d)  =>  50  0,5  +  { 32 + 18 ημ(5t + π/2) } 1,5  =  F_Γ 1   =>  F_Γ (t)  =  73 + 27 ημ(5t + π/2)  

 ροπές ως προς Γ :   Mg (L/2 - d)  =  F_ελατ d  +  F_Β (L - 2d)   =>  50  0,5  =  { 32 + 18 ημ(5t + π/2) } 0,5  +  F_Β  1  =>   F_Β (t)  =  9 - 9 ημ(5t + π/2)