6.

Η ράβδος OΔ του σχήματος είναι ομογενής, έχει μάζα 6m, μήκος L και συνδέεται με άρθρωση στο σημείο Ο με κατακόρυφο τοίχο. Η ράβδος μπορεί να περιστρέφεται χωρίς τριβές σε κατακόρυφο επίπεδο, γύρω από τον οριζόντιο άξονα που διέρχεται από το άκρο Ο.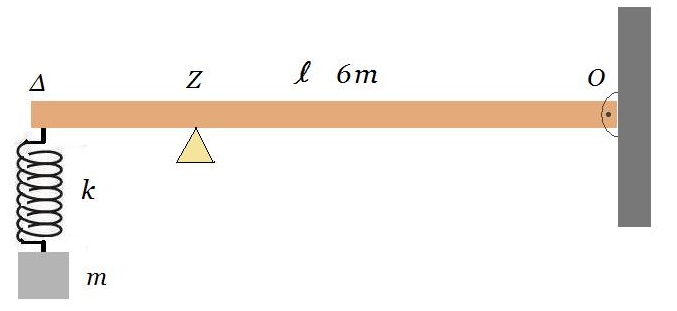
Η ράβδος ισορροπεί οριζόντια με τη βοήθεια του στηρίγματος στο σημείο Ζ, ενώ στο άκρο της Δ είναι συνδεδεμένο ιδανικό ελατήριο με σταθερά Κ. Στο κάτω άκρο του ελατηρίου είναι δεμένο σώμα με μάζα m, το οποίο εκτελεί κατακόρυφη απλή αρμονική ταλάντωση. Ποια είναι η μέγιστη ταχύτητα του σώματος m, ώστε κατά τη διάρκεια της ταλάντωσής του η ράβδος ΟΔ να μην ανατρέπεται;

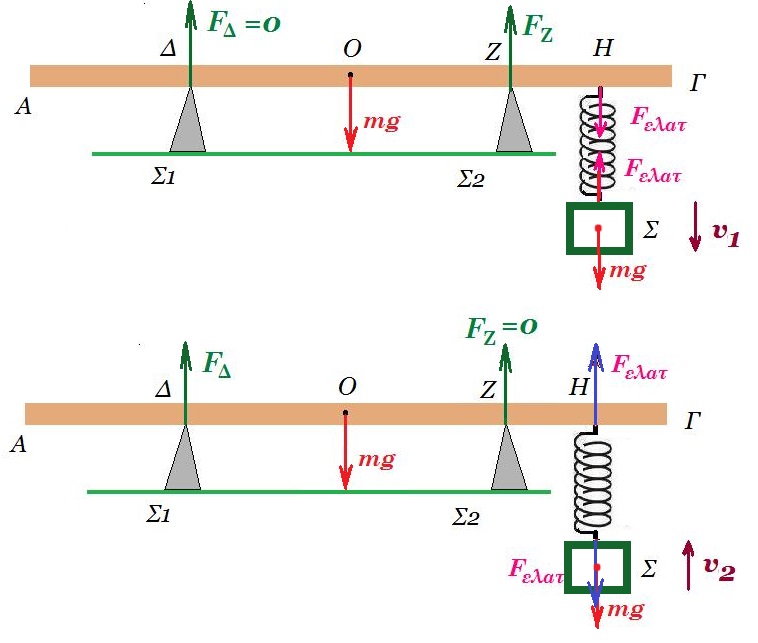
7.    Ομογενής δοκός ΑΓ μικρού πάχους,  μάζας m  και  μήκους (ΑΓ) = l  ισορροπεί οριζόντια.   Η δοκός ακουμπά σε δύο μυτερά στηρίγματα (Σ1) και (Σ2) στα σημεία Δ και Ζ αντίστοιχα, τα οποία απέχουν από τα άκρα της δοκού αποστάσεις (ΑΔ) = l /4  και (ΖΓ) = l /4.  Από τα στηρίγματα η δοκός δέχεται κατακόρυφες δυνάμεις. Από σημείο Η της δοκού που απέχει από το άκρο Γ απόσταση (ΓΗ) = l /8,  κρέμεται κατακόρυφο ιδανικό ελατήριο σταθεράς K, στο κάτω άκρο του οποίου είναι στερεωμένο και ισορροπεί μικρό σώμα (Σ)  ίδιας μάζας m με τη δοκό. Το σύστημα βρίσκεται στην επιφάνεια της γης, όπου το μέτρο της επιτάχυνσης της βαρύτητας ισούται με g.
Δίνουμε στο σώμα (Σ) κατακόρυφη ταχύτητα μέτρου υ₁  προς τα κάτω, οπότε  καθώς  κατέρχεται εκτελώντας απλή αρμονική ταλάντωση σταθεράς  D=K, η δοκός οριακά δεν εκτρέπεται από την οριζόντια θέση.
Στη συνέχεια, φέρνουμε ξανά το σώμα (Σ) στη θέση ισορροπίας του, όπου ισορροπεί.  Δίνουμε στο σώμα κατακόρυφη ταχύτητα μέτρου  υ₂  προς τα πάνω, οπότε καθώς  ανέρχεται εκτελώντας απλή αρμονική ταλάντωση σταθεράς D=K, η δοκός οριακά δεν εκτρέπεται από την οριζόντια θέση.   Ο λόγος   υ₁ /υ₂   ισούται με: 

α.  4/7           β.  5/7           γ.  6/7            δ.  7/5

6.

  ισορροπία σώματος :   m g = k x₀  =>  x₀ = mg/k  επιμήκυνση ελατηρίου   x₀ προς τα κάτω       

  ανατροπή έχουμε όταν το σώμα κινείται προς τα πάνω και το ελατήριο είναι συσπειρωμένο έστω x₁

  ροπές ως προς Ο :   F_ελατ l  =  6m g l/2  =>  F_ελατ = 3mg  =>  k x₁ = 3mg =>  x₁ = 3mg/k  

      η μέγιστη συσπείρωση του ελατηρίου για να μην ανατραπεί η ράβδος  x₁ προς τα πάνω    

 το μέγιστο πλάτος ασφαλούς ταλάντωσης :  Α_max =  x₀  + x₁ = mg/k + 3mg/k = 4mg/k  

   x = A ημωt        v = Aω συνωt       υ_max = A_max ω = 4mg/k (k/m)^½  = 4 g(m/κ)^½   

7.

    ισορροπία Σ :       m g = k Δl  (1)  όπου  Δl = επιμήκυνση ελατηρίυ

  ½ k A₁²  =  ½ m v₁²              v₁ = ω Α₁               F_ελατ = k (Δl + A₁) =  mg + k A₁  για το σώμα προς τα πάνω  ενώ  για τη δοκό προς τα κάτω    

ροπές ως προς Ζ :   m g l/4  -  F_Δ l/2  -  F_ελατ l/8  =  0  => ^F_Δ=0   mg l/4  = ( mg + k A₁ ) l/8  =>

            =>  2 mg = mg + k A₁  =>   mg  =  k A₁  =  k/ω v₁    (2)    

    ½ k A₂ ²  =  ½ m v₂²              v₂ = ω Α₂               F_ελατ = k ( - Δl + A₂) =  - mg + k A₂  

ροπές ως προς Δ : 

- mg l/4  +  F_Ζ l/2  +  F_ελατ (l/2+l/8) = 0  =>^F_Z=0 - mg l/4  + (- mg + k A₂ ) 5l/8  =  0 =>

  => - mg l/4  - mg 5l/8 + k A₂ 5l/8  =  0  =>

  =>  mg 7/8 l  = k A₂ 5/8 l  =>  7/5 mg  =  k A₂ =  k/ω v₂   (3)      

            (2) / (3)  =>   υ₁ / υ₂ = 5/7                             

από (1), (2) =>  Α₁ = Δl       από (1), (3) =>  Α₂ = 7/5 Δl