ΘΕΜΑ Δ

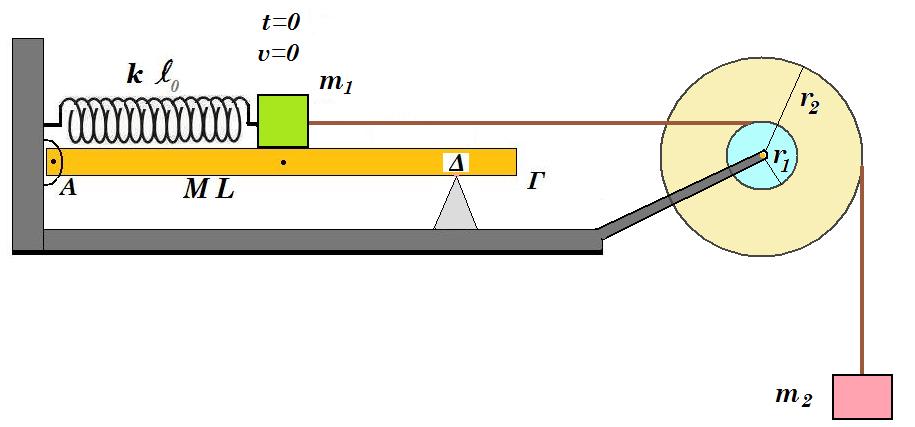
Λεία οριζόντια σανίδα ΑΓ μήκους L = (ΑΓ) = 2 m και μάζας Μ = 3 Kg αρθρώνεται στο άκρο της Α σε κατακόρυφο τοίχο. Σε απόσταση d = 0,4 m από το άκρο Γ, η σανίδα στηρίζεται στο σημείο Δ  ώστε να διατηρείται οριζόντια. Ιδανικό αβαρές ελατήριο σταθεράς k = 500 Ν/m συνδέεται με το ένα άκρο του στον τοίχο και το άλλο σε σώμα Σ₁ μάζας m₁ = 1 Kg. Το ελατήριο βρίσκεται στο φυσικό του μήκος, ο άξονάς του είναι οριζόντιος και διέρχεται από το κέντρο μάζας του σώματος Σ₁. Το κέντρο μάζας του σώματος Σ₁ βρίσκεται σε απόσταση L/2 από τον τοίχο, το Σ₁ συνδέεται με το ένα άκρο αβαρούς μη εκτατού νήματος το οποίο έχει τυλιχθεί πολλές φορές σε διπλή τροχαλία όπως στο σχήμα. Άλλο σώμα Σ₂  μάζας m₂ = 1 Kg  συνδέεται με το ένα άκρο αβαρούς μη εκτατού νήματος το οποίο έχει τυλιχθεί πολλές φορές στην τροχαλία όπως στο σχήμα.  Η τροχαλία θεωρείται αμελητέας μάζας που μπορεί να στρέφεται χωρίς τριβές περί άξονα κάθετο στο επίπεδό της που διέρχεται από το κέντρο της, ισχύει δε  r₁ = 0,1 m  και  r₂ = 0,2 m.  
Συγκρατούμε τα σώματα σε ακινησία, το ελατήριο βρίσκεται στο φυσικό του μήκος, η τροχαλία είναι ακίνητη  και  την στιγμή t₀=0  αφήνουμε το σύστημα να κινηθεί.  Να μελετηθεί η κίνηση των σωμάτων.

Α)  Το σώμα (2) κατεβαίνει με επιτάχυνση  α₂  και το σώμα (1) κινείται προς τα δεξιά με επιτάχυνση  α₁  ενώ η τροχαλία στρέφεται με γωνιακή επιτάχυνση  α_γων.  Δείξτε ότι  α₂ = 2 α₁.  

B)  Δείξτε ότι η μέγιστη επιμήκυνση του ελατηρίου κατά την κίνηση των σωμάτων είναι :  0,08 m.

Γ)  Όταν η επιμήκυνση του ελατηρίου είναι  0,04 m   υπολογίστε τις ταχύτητες των σωμάτων.

Δ)  Δείξτε ότι το σώμα (1)  εκτελεί  Α.Α.Τ.  με εξίσωση :  x(t) = 0,04 ημ(10.t + θ)    Πόση είναι η αρχική φάση θ ;

Ε)  Εκφράστε την δύναμη ελατηρίου που δέχεται το σώμα συναρτήσει της απομάκρυνσης και σχεδιάστε το διάγραμμα.

ΣΤ) Εκφράστε την δύναμη που δέχεται η σανίδα στο στήριγμα Δ  συναρτήσει της απομάκρυνσης και σχεδιάστε το διάγραμμα.

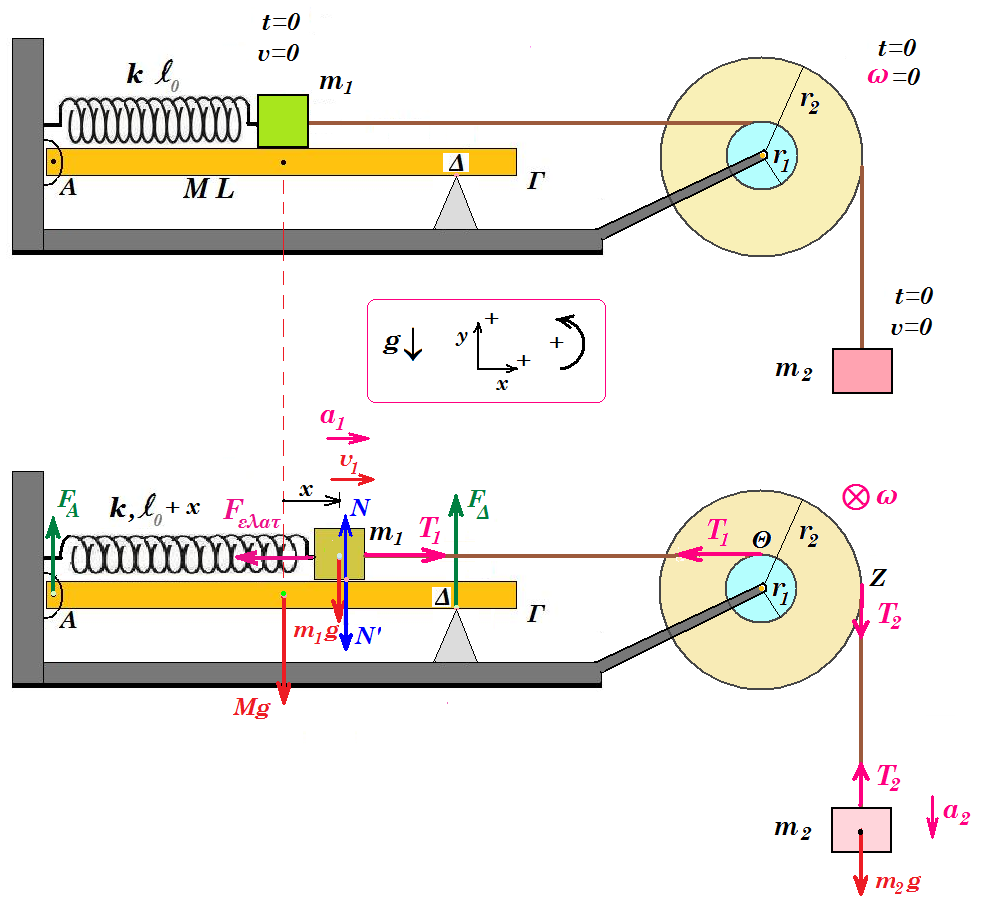
κίνηση σώματος Σ₂ :  m₂ g  -  T₂ = m₂ a₂  => 10 - T₂ = 1 a₂   (1)

η τροχαλία περισρτρέφεται με σταθερή συχνότητα  διότι η ροπή αδράνειας της είναι μηδενική

περιστροφή τροχαλίας :  T₁ r₁ = T₂ r₂  =>  T₁  0,1m = T₂  0,2m  =>  T₁ = 2.T₂   (2)

κίνηση σώματος Σ₁ : T₁ - F_ελατ = m₁ a₁ => T₁ - k.x = m₁ a₁ => T₁ - 500.x = 1 a₁  (3)

 v₂  =  v_Z  =  ω r₂  =  ω 2r₁  =  2 v_Θ  =  2 v₁  =>  a₂ = 2 a₁   (4)

2*(1) + (3) =>  20  -  2.T₂  + T₁ - 500.x  = 2 a₂ + 1 a₁  =>   

                 =>  20 - 500.x = 2 a₂ + 1 a₁  =>⁽⁴⁾  20 - 500.x = 4.a₁ + a₁ => 

                 =>  20 - 500.x = 5.a₁  =>  4 - 100.x = a₁ = x''(t)   (5)          - ω² x = a 

το σώμα Σ₁  εκτελεί Α.Α.Τ.  με  ω² = 100 =>  ω = 10 rad/s

η (5)  λέει ότι η επιτάχυνση του Σ₁  μειώνεται όσο η αποάκρυνση x  αυξάνεται  έτσι κάποια στιγμή  α₁ = 0   =>  x = 0,04 m

το Σ₂ αρχίζει να κατεβαίνει επιταχυνόμενο  η τροχαλία περιστρέφεται με σταθερή συχνότητα διότι η μάζα της είναι αμελητέα  το Σ₁  αρχίζει να επιταχύνεται προς τα δεξιά   

επειδή   α₂ = 2.α₁  το Σ₂  διανύει διπλάσιο διάστημα από το Σ₁ στο ίδιο χρόνο  

 x₂ = ½ a₂ t² = ½ 2.a₁ t² = 2.x₁   

m₂ g h = ½ k x² => m₂ g 2.x = ½ k x² => 10 2.x = ½ 500 x² => x = 0  ή x = 20/250 = 0,08m  μέγιστη επιμήκυνση ελατηρίου

 διατήρηση ενέργειας από την στιγμή μηδέν μέχρις ότου  το ελατήριο επιμηκυνθεί κατα  x = 0,04 m

 m₂ g h  =  ½ m₁ v₁²  +  ½ m₂ v₂²  +  ½ k x²  =>  m₂ g 2.x  =  ½ 1 v₁²  +  ½ 1 4.v₁²  +  ½ k x²  =>

=>  10 2.0,04  =  ½ 1 v₁²  +  ½ 1 4.v₁²  +  ½  500  0,04²  =>

=>  0,8  =  0,5 v₁²  + 2.v₁²  + 0,4  =>  2,5 v₁²  =  0,4  =>  v₁² = 4/25  =>  v₁ = 0,4 m/s  

   v₂ = 0,8 m/s 

η δυναμική ενέργεια βαρύτητας του Σ₂  μετατρέπεται σε κινητική ενέργεια των σωμάτων  και της τροχαλίας  και  δυναμική ενέργεια στο ελατήριο 

κάποια στιγμή  ΣF₍₁₎ = 0  => T₁ - F_ελατ = 0  =>  T₁ = 500.x  

τότε  ΣF₍₂₎ = 0  => m₂ g  - T₂ = 0  =>  T₂ = 10 Ν   οπότε  Τ₁ = 20 Ν   άρα  x = 20/500 m = 0,04 m  

εκείνη τη στιγμή  το ελατήριο έχει αποθηκεύσει ενέργεια  U_ελατ = ½ k x² = ½ 500 0,04² = 0,4 J

το Σ₂ έχει διανύσει διπλάσια απόσταση δηλαδή 0,08 m  άρα χάσει βαρυτική δυναμική ενέργεια : m₂ g h = 10  0,08 = 0,8 J

K₁ + K₂ = ½ m₁ v₁² + ½ m₂ v₂² = ½ 1 v₁² + ½ 1 4.v₁² = 2,5 v₁² = 0,8 J - 0,4 J  =>

    =>  v₁² = 0,4/2,5 = 0,16  =>  v₁ = 0,4 m/s     άρα    v₂ = 0,8 m/s 

λόγω ταχύτητας το Σ₁  συνεχίζει την κίνησή του προς τα δεξιά  όταν x = 0,05 m  το ελατήριο θα του ασήσει δύναμη F_ελατ =  k x =  500  0,05  =  25 Ν (προς αριστερά)  >  20 Ν = Τ₁   άρα  επιβραδύνεται

από την  (5) =>  4 - 100.x = a₁ =>  4 - 100.0,05 = a₁  =>  α₁ = - 1 m/s²  επιβράδυνση

x(t) = A ημ(10.t + φ)  =>  x(t) = 0,04 ημ(10.t + 3π/2)      το Σ1  ξεκινά από τη θέση   x = -Α = -0,04m

      v(t) = 0,4 συν(10.t + 3π/2)              α(t) = - 4 ημ(10.t + 3π/2)

ΣF = m₁ a₁  =>  T₁  +  F_ελατ  =  m₁ a₁     (3)            T₁ = 2.T₂             a₂ = 2 a₁   

ΣF = m₂ a₂  =>   m₂ g - T₂ = m₂ a₂  =>  2 m₂ g  -  2T₂  =  2m₂ 2 a₁     (4)    

   (3) + (4) =>  T₁  +  F_ελατ  +  2 m₂ g -  2T₂  =  m₁ a₁  +  4 m₂ a₁    =>

         =>   F_ελατ  +  2 m₂ g  =  m₁ a₁  +  4 m₂ a₁   =>   F_ελατ  +  20  =  5 a₁  =>  

        =>  F_ελατ  =  - 20  - 20 ημ(10.t + 3π/2) 

   F_ελατ  =  - 20  - 20 x / 0,04  = - 20 - 500 x  = - 500 ( 0,04 + x )   - 0,04 m  £  x £  +0,04m   

                                                                                                                 0  ³  F_ελατ  ³  - 40 Ν

 ροπές ως προς Α :  Στ_(Α) = 0  =>  F_Δ (ΑΔ)  -  Ν' (l/2 + x)  -  Mg l/2  =  0  =>

 =>  F_Δ  1,6  -  10  (1 + x)  -  30  1  =  0  =>  F_Δ = (40 + 10 x) / 1,6  =>  F_Δ(x) = 25 + 6,25 x