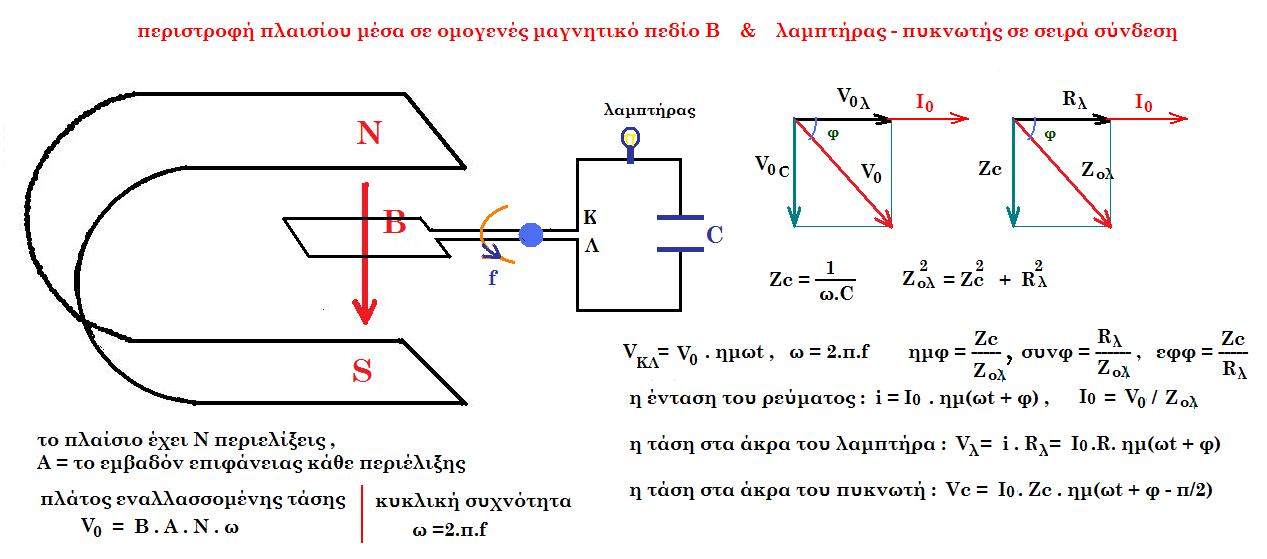
V = VR + VC     =>    V0 . ημωt = i . R + q / C      =>       V0 . ημωt = R . dq/dt +  q / C      =>     dq/dt +  q / R.C = V0/R . ημωt    (1)  

i = I0 . ημ(ωt + φ)  ,    q = - Q . συν(ωt + φ)    =>   i = dq/dt = Q.ω. ημ(ωt + φ)  

 (1) =>   Q.ω. ημ(ωt + φ) + [ - Q / R.C . συν(ωt + φ) ]  = V0/R . ημωt  =>   Q.ω. ημ(ωt + φ)  - Q / R.C . συν(ωt + φ) = V0/R . ημωt  =>

      =>    Q.ω. ( ημωt . συνφ  + συνωt . ημφ )  - Q / R.C. ( συνωt . συνφ - ημωt . ημφ ) = V0/R . ημωt        εξισώνουμε τους  συντελεστές ως προς   συνωt   και ημωt  :

συνωt :  Q.ω.  ημφ  - Q / R.C.  συνφ  =  0    =>  ω.  ημφ   = 1 / R.C.  συνφ   =>   εφφ  =  1 / ω.C.R  = ZC / R 

ημωt  :    Q.ω.   συνφ   +   Q / R.C.  ημφ    =   V0/R       =>        Q.ω. R / Z   +  ( Q / R.C ) . (1/ωC) / Z    =   V0/R    =>     Q.ω. R2  +  Q.ω. (1/ωC)2  = V0 . Ζ =>    Q.ω.[ R2  + (1/ωC)2 ] = V0 . Ζ

      =>    Q.ω. Ζ2 = V0 . Ζ   =>    Q.ω  = V0 / Ζ  =  Ι0   μέγιστη τιμή ( πλάτος ) ρεύματος  

από τις σχέσεις     εφφ = ημφ / συνφ     και     ημ2 φ + συν2 φ = 1    έχουμε :       εφ2 φ + 1 = 1 / συν2 φ   (4)   και     1/εφ2 φ + 1 = 1 / ημ2 φ   (5)

η (4) => 1 / συν2 φ = ( 1 / ωRC )2 + 1 =>   συν2 φ = (ωRC)2 / [ 1 + (ωRC)2 ]     =>   συν2 φ = R2 / [ (1/ωC)2 + R2 ]    =>   συνφ = R / [ (1/ωC)2 + R2 ]½    =>   συνφ = R / Z

η (5) => 1 / ημ2 φ = ( ωRC )2 + 1   =>    ημφ = 1 / [ (ωRC)2 + 1 ]½  =  (1/ωC) / [ (1/ωC)2 + R2 ]½   =    ZC / Z   =>   ημφ = ZC / Z        

η τάση στα άκρα του λαμπτήρα είναι : VR = i . R = V0 . R / Z . ημ(ωt+φ) ,    το πλάτος της τάσης είναι :  V0,R =  Ι0 . R  =  V0 / Z . R  =  V0 . R /  [ (1/ωC)2 + R2 ]½    

αν η συχνότητα  ω  είναι πολύ μικρή  ( χαμηλές συχνότητες )  ( ω ---> 0 )   τότε  :   V0,R  ---->  0     διότι  1 /  ωC  ----> + οο   και   Ζ ----> 0

αν η συχνότητα ω είναι πάρα πολύ μεγάλη  ( ω ---> + οο )  τότε :  V0,R =  V0     διότι  1 / ωC ----> 0   και   Ζ   ----> R

     η συνάρτηση   g(ω) = R / [ (1/ωC)2 + R2 ]1/2    είναι  αύξουσα  διότι   g' (ω) > 0 ,  ω > 0

                                                                           g' (ω) =   R / (ω3. C2) . [ (1/ωC)2 + R2 ]-3/2   >  0

 

το πλάτος της τάσης στα άκρα του πυκνωτή  είναι :   V0,C = Ι0 . Ζc =  V0 / Z . Ζc  =  V0 .(1 / ωC)  /  [ (1/ωC)2 + R2 ]½  

αν η συχνότητα  ω  είναι πολύ μικρή  ( ω --> 0 )   τότε :    V0,C = V0   

αν η συχνότητα  ω  είναι πολύ μεγάλη  ( ω --> + οο )  έχουμε :  ΖC = 1/ωC --> 0  και  Ζ  -->  R    οπότε :  V0,C  -->  0     

       θεωρούμε τη συνάρτηση : ψ(ω)  =  ZC / Z  =  (1 / ωC) . [ (1/ωC)2 + R2 ]1/2      =>      ψ(ω) = [ 1 + (ωCR)2 ]-1/2    
        η 1η παράγωγος : ψ'(ω) = -½ . [ 1 + (ωCR)2 ]-3/2 . { 1 + (ωCR)2 }' =  = - ½ . [ 1 + (ωCR)2 ]-3/2 . 2.ω. (CR)2 = - [ 1 + (ωCR)2 ]-3/2 . ω. (CR)2

                               επειδή ω > 0   και η υπόριζος ποσότητα θετική   =>   ψ'(ω) < 0    άρα    ψ(ω)   φθίνουσα