φυσική    Γ' ΛΥΚΕΙΟΥ

ΘEΜΑ Δ. 

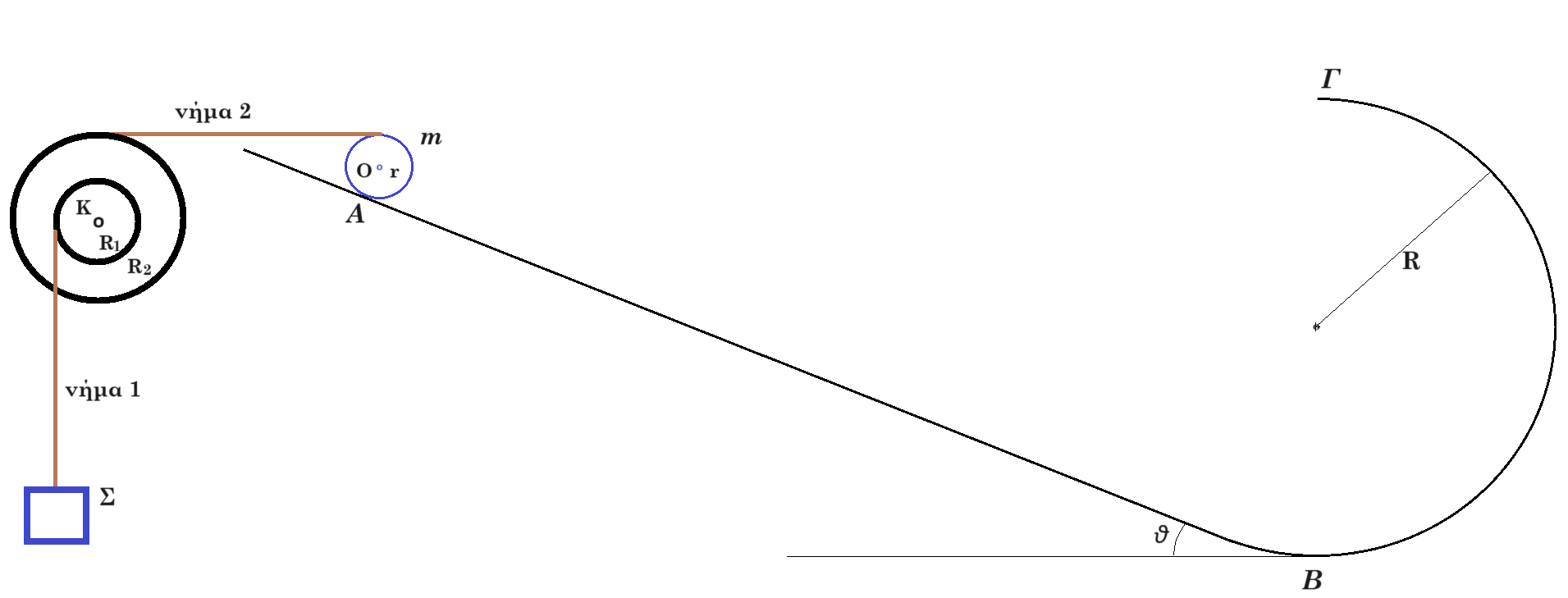
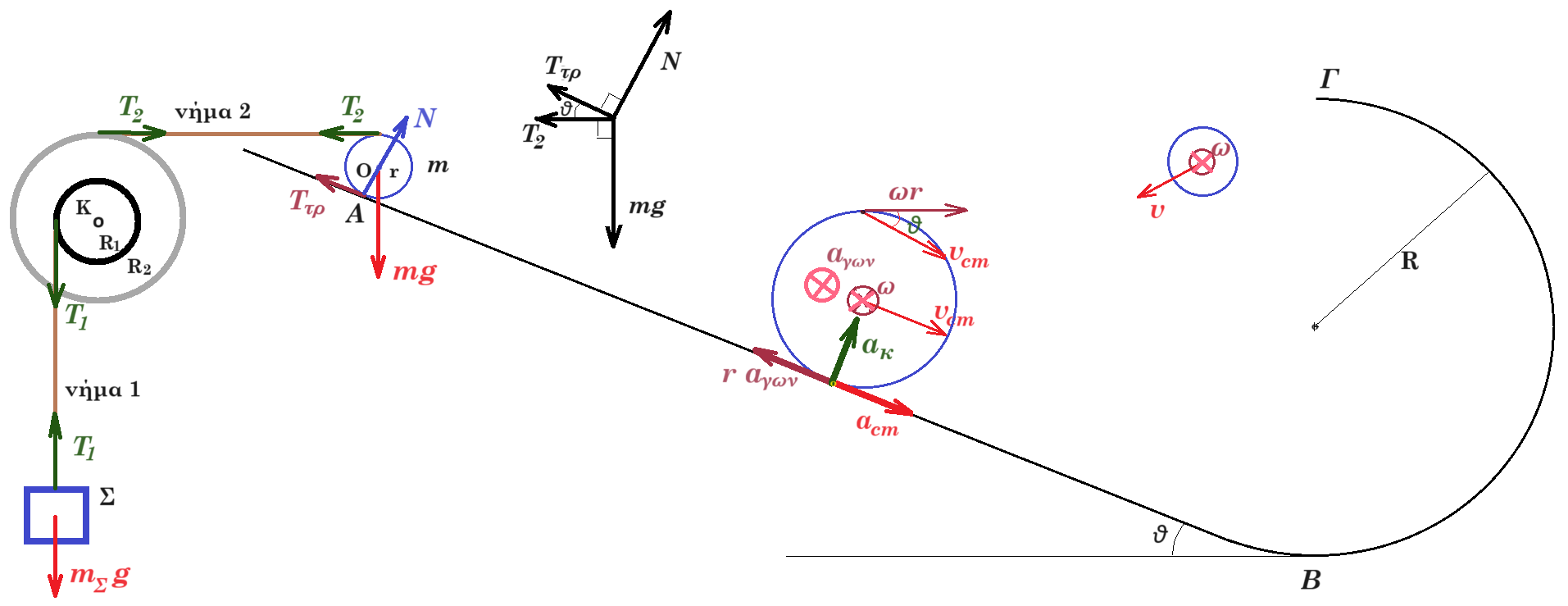
Θεωρούμε την διάταξη του σχήματος, σε κατάσταση ισορροπίας, σε κατακόρυφο επίπεδο.  Στη θέση Α του κεκλιμένου επιπέδου ισορροπεί κυκλική στεφάνη μάζας m = 3kg ακτίνας r = 0,1m.  Το κεκλιμένο επίπεδο γωνίας κλίσεως θ, ( ημθ = 0,6  συνθ = 0,8 ) στην βάση του συνδέεται με κατακόρυφο ημικύκλιο ακτίνας R = 1m.  Η στεφάνη στο άνω της άκρο συνδέεται με οριζόντιο αβαρές μη εκτατό νήμα 2 (σταθερού μήκους) με τροχαλία μάζας Μ=5kg   εσωτερικής ακτίνας R₁ = 0,2m   εξωτερικής ακτίνας R₂ = 0,5m.  Η τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από άξονα που διέρχεται από το κέντρο της Κ ( σταθερό ακίνητο σημείο )  και είναι κάθετος στο επίπεδο της. Γύρω από την τροχαλία έχουμε τυλίξει αρκετές φορές αβαρές μη εκτατό νήμα 1  το οποίο συνδέεται με σώμα Σ.  

Δ1.   Βρείτε την μάζα του σώματος Σ.                                μονάδες 12

Κάποια στιγμή ( t₀=0 ) αφαιρούμε το νήμα 2,  οπότε η στεφάνη κατέρχεται επί του κεκλιμένου επιπέδου κυλιόμενη ( δεν ολισθαίνει )  ενώ το σώμα Σ  κινείται κατακόρυφα προς τα κάτω  και η τροχαλία περιστρέφεται γύρω από τον άξονά της χωρίς τριβές έχοντας γωνιακή επιτάχυνση  α_γων = 10/3 m/s².  

Δ2.  Εάν η μάζα του σώματος Σ είναι m_Σ = 2,5 kg  εκφράστε την στροφορμή του συναρτήσει του χρόνου.           μονάδες 8

Δ3.  Τη χρονική στιγμή t₀ = 0  η στεφάνη αρχίζει να κατέρχεται κυλιόμενη επάνω στο κεκλιμένο επιπέδο  ενώ το κέντρο της έχει επιτάχυνση  α_cm = 3 m/s².  Τη χρονική στιγμή t₁=1s  βρείτε την ταχύτητα του ανώτερου σημείου της στεφάνης   καθώς  και την επιτάχυνση του σημείου επαφής της στεφάνης με το κεκλιμένο επίπεδο.                 μονάδες 10    

Δ4.  Η στεφάνη κυλίεται (δεν ολισθαίνει) κινούμενη στο κεκλιμένο επίπεδο,  ανέρχεται κυλιόμενη στο ημικύκλιο  και διέρχεται από την ανώτατη θέση Γ του ημικυκλίου έχοντας ταχύτητα μέτρου  3m/s.   Βρείτε την δύναμη που δέχεται από το ημικύκλιο στο σημείο Γ  και  την γωνιακή ταχύτητάς της ( διεύθυνση, φορά, μέτρο )  μετά από  0,2 sec  αφού περάσει το σημείο Γ.          μονάδες 10    

   επιτάχυνση βαρύτητας  g = 10 m/s²     

ΘEΜΑ Γ.

Τα σώματα Σ1 και Σ2 του σχήματος με μάζες  m₁ = 0,6 kg  και  m₂ = 0,2 kg αντίστοιχα, ισορροπούν στο ίδιο οριζόντιο επίπεδο, δεμένα με αβαρή νήματα που έχουμε τυλίξει πολλές φορές σε διπλή τροχαλία αμελητέας μάζας.  Τη στιγμή t₀=0  προσδένουμε βαρίδι στο γάντζο που υπάρχει κάτω από το Σ1 με συνέπεια να χαλάει η ισορροπία.   Το σύστημα Σ1-βαράκι κατέρχεται επιταχυνόμενο, η τροχαλία στρέφεται με γωνιακή επιτάχυνση και το Σ2 ανέρχεται επιταχυνόμενο.  Πόση είναι η μάζα του βαριδίου εάν τη στιγμή  t₁ = 2s  τα κέντρα βάρους των Σ1 και Σ2 απέχουν απόσταση 3,2m;   

  ισορροπία συστήματος :  Στ_(Κ) = 0  =>  m₁ g r₁  -  m₂ g r₂  =  0  =>  m₁ r₁  =  m₂ r₂  =>

                                                         =>  0,6 r₁  = 0,2 r₂  =>  r₂ = 3 r₁      (1)    

  a₂ =  a_γων r₂  = a_γων 3 r₁  = 3 a₁  =>  a₂ = 3 a₁            v₂ = 3 v₁         y₂ = 3 y₁    

  y₂ + y₁ = 3,2 m  =>  4 y₁ = 3,2 m  =>  y₁ = 0,8 m              y₂ = 2,4 m    

  y₁ = 0,5 a₁ t²  =>  0,8  =  0,5 a₁  4  =>  a₁ = 0,4 m/s²         a₂ = 1,2 m/s²    

 (m₁ + m) g  -  T₁  = (m₁ + m) a₁       (2) 

  T₁ r₁ = T₂ r₂  =>  T₁ r₁ = T₂ 3 r₁  =>  T₁ = 3 T₂      (3)

 T₂ - m₂ g = m₂ a₂  = m₂ 3 a₁   =>   3 T₂  -  3 m₂ g  =  9 m₂ a₁     (4) 

  (2) + (4) =>   (m₁ + m) g  -  T₁  +  3 T₂  -  3 m₂ g  =  (m₁ + m) a₁  + 9 m₂ a₁   

                =>   (m₁ + m) g  -  3 m₂ g  =  (m₁ + m) a₁  + 9 m₂ a₁   

                =>   (m₁ + m - 3 m₂) g  =  (m₁ + m + 9 m₂) a₁   

                =>   (0,6 + m - 0,6) 10  =  (0,6 + m + 1,8) a₁   

                =>   m 10  =  (m + 2,4) 0,4   =>   m = 0,1 kg   μάζα βαριδίου

                     ΛΥΣΗ

Δ1.   ισορροπία  Σ :  Τ₁  =  m_Σ g     (1)  

 ισορροπία τροχαλίας :   Στ_(Κ)  =  0  =>  Τ₂ R₂  -  T₁ R₁  =  0  =>  T₂  0,5  =  T₁  0,2  => 

                                                       =>   T₂  =  0,4 T₁   =  0,4 m_Σ g  =>  Τ₂ = 4 m_Σ     (2)              

ισορροπία στεφάνης :   Στ_(Ο)  =  0  =>  Τ₂ r  -  Τ_τρ r  =  0  =>  Τ₂ = Τ_τρ    (3)    

ΣF_x = 0  =>   N ημθ  -  Τ₂  -  Τ_τρ συνθ  =  0  =>⁽³⁾  N ημθ  -  Τ₂  -  Τ₂ συνθ  =  0  =>  

              =>  N 0,6  -  Τ₂  -  Τ₂ 0,8  =  0  =>  Ν  =  3 Τ₂     (4)   

ΣF_y = 0  =>  N συνθ  -  m g  +  Τ_τρ ημθ  =  0  =>  3Τ₂  0,8  -  3 10  +  Τ₂  0,6  =  0   =>  Τ₂ = 10 Ν

                     άρα  η (2) =>  Τ₂ = 4 m_Σ  =>  10  = 4 m_Σ  =>  m_Σ = 2,5 kg 

Δ2.   επιτάχυνση σώματος Σ :  a_Σ = α_γων R₁  =  10/3 rad/s²  0,2 m  =  2/3 m/s²   

  ταχύτητα σώματος Σ :   v_Σ  =  a_Σ t  =  2/3 t       

στροφορμή του σώματος Σ  ως προς το σημείο Κ :   L  =  m_Σ  v_Σ R₂  =  2,5   2/3 t  0,5  =>   L(t)  =  5/6 t    

Δ3.   a_cm = α_γων r  =>  3 m/s²  = α_γων  0,1 m  =>  a_γων = 30 rad/s²       ω = α_γων t = 30 rad/s² 1 s = 30 rad/s    

           υ_cm = = ω r = 30 rad/s  0,1 m = 3 m/s  

  υ²  =  υ_cm²  +  (ω r)²  +  2 υ_cm  ω r  συνθ  =  2 υ_cm² ( 1 + συνθ ) = 2 3²  (1 + √3/2 ) =  18 (1 + √3/2 ) =  9 (2 + √3)  =>  υ  = 3 √(2 + √3) m/s    

α_γων = M.g.ημθ / (Ι/R² + Μ).R  =>  α_γων = M.g.ημθ / ( Μ + Μ).R   =>  α_γων = M.g.ημθ / 2Μ.R   => 

       =>   α_γων =  g.ημθ / 2R   =>  α_γων = 10 0,6 / 2 0,1  =>  α_γων =  30 rad/s²

στο σημείο Ε  η στεφάνη  έχει  τρεις επιταχύνσεις  την επιτάχυνση του κέντρου μάζας ,  την γωνιακή  και  την  κεντρομόλο    αλλά  η επιτάχυνση του κέντρου μάζας  και η γωνιακή είναι αντίθετες και έχουν συνισταμένη μηδέν  ενώ   η κεντρομόλος ισούται με  α_κ  =  υ² / r  =  ω² r  =  30²  0,1  =  90 m/s²    

Δ4.  όταν η στεφάνη διέρχεται από την ανώτερη θέση Γ υ_Γ = 3 m/s :  ΣF_y = F_κ  =>  mg  + Ν = m v_Δ²/(R - r)  =>   30  + Ν =  3  3² / (1 - 0,1)  =>  Ν  =  27/0,9 - 30 = 0    άρα  μόλις διέρχεται από την ανώτερη θέση Γ του ημικυκλίου  διότι ισχύει Ν = 0  

η στεφάνη στον αέρα δεν δέχεται δύναμη που να δημιουργεί ροπή  συνεπώς  η γωνιακή ταχύτητά της είναι σταθερή  ω = υ_Γ / r = 3 m/s  /  0,1 m  = 30 rad/s