επαναληπτικές  ΣΕΠ 2019

ΘΕΜΑ Γ
Γραμμικό ομογενές ελαστικό μέσο μεγάλου μήκους εκτείνεται κατά μήκος του θετικού ημιάξονα Οx. Στο σημείο Ο (στη θέση x=0) είναι τοποθετημένη σημειακή πηγή που εκτελεί αρμονική ταλάντωση με εξίσωση απομάκρυνσης της μορφής y=Α∙ημωt, με αποτέλεσμα να δημιουργείται ένα εγκάρσιο αρμονικό κύμα, το οποίο διαδίδεται χωρίς απώλειες ενέργειας προς τη θετική κατεύθυνση του άξονα Ox. Η γραφική παράσταση της φάσης φ σε συνάρτηση με το χρόνο t, για ένα σημείο Ρ του ελαστικού μέσου, το οποίο βρίσκεται στη θέση x_P=1m, δίνεται από το σχήμα.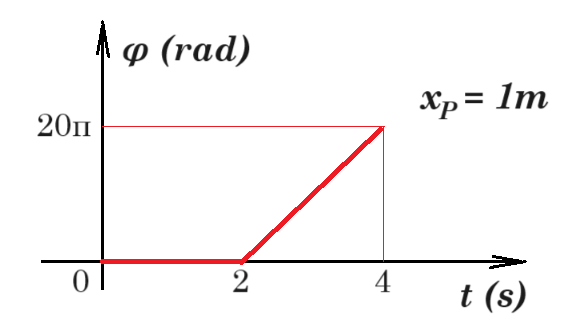

Η ενέργεια ταλάντωσης μιας στοιχειώδους μάζας Δm=2∙10^-6 kg του ελαστικού μέσου είναι ίση με 16π²∙10^-8 J.

Γ1.  Να υπολογίσετε τo πλάτος ταλάντωσης Α της πηγής του κύματος .    Μονάδες 6
Γ2.  Να γράψετε την εξίσωση του αρμονικού κύματος στο διεθνές σύστημα μονάδων (SI).    Μονάδες 6

Ένα σημείο Σ του ελαστικού μέσου βρίσκεται στη θέση x_Σ=1,15m.
Γ3.  Να υπολογίσετε το μέτρο της ταχύτητας του σημείου Σ (μονάδες 6) και την κατεύθυνσή της (μονάδα 1) τη χρονική στιγμή που το σημείο Ρ διέρχεται από τη θέση ισορροπίας του με θετική ταχύτητα.           Μονάδες 7
Γ4.  Να γράψετε την εξίσωση της απομάκρυνσης του σημείου Σ με το χρόνο, από τη χρονική στιγμή t=0 μέχρι τη χρονική στιγμή t₁=2,7s (μονάδες 3) και να την σχεδιάσετε σε βαθμολογημένους άξονες (μονάδες 3).    Μονάδες 6

 Να μη γίνει αριθμητική αντικατάσταση του αριθμού π.

Γ1.      φ  =  10π (t - 2)  =  10πt  -  20π   

  φ = ωt - 2πx/λ  =>  10πt  -  20π  = ωt - 2π 1/λ    =>    ω = 10π rad/s        λ = 2π / 20π = 0,1 m

 Ε = ½ Δm v_max²  =>  16π²∙10^-8 = ½  2∙10^-6  v_max² =>  v_max = 0,4π m/s  = ω Α = 10π Α =>  Α = 0,04 m

Γ2.         y  =  0,04 ημ(10πt  -  20πx)      ω = 10π rad/s     T = 2π / ω = 0,2 s  

Γ3.       x_Σ  =  1,15 m

    y_Σ  =  0,04 ημ(10πt  -  20π 1,15)  =  0,04 ημ(10πt  -  23π)  =  0,04 ημ(10πt  -  π)  = - 0,04 ημ(10πt)          v_Σ  =  - 0,4π συν(10πt)       

   x_Ρ  =  1 m

    y_Ρ  =  0,04 ημ(10πt  -  20π 1)  =  0,04 ημ(10πt  -  20π)  =  0,04 ημ(10πt)          v_Ρ  =  0,4π συν(10πt)      y_Ρ  = 0  =>  ημ(10πt)  =  0  =>  συν(10πt)  =  1  =>  v_Ρ  =  0,4π m/s 

    y_Σ  =  - 0,04 ημ(10πt)  =  0    =>   v_Σ = - 0,4π συν(10πt)  =  - 0,4π m/s

Γ4.       x_Σ  =  1,15 m        y_Σ  =  0,04 ημ(10πt  -  23π)            t > 2,3 s  

     2,7 s  =  2,3 s  +  0,4 s  =   2,3 s  +  2 T