ΘΕΜΑ Γ
Στην επιφάνεια ενός υγρού που ηρεμεί βρίσκονται δύο σύγχρονες και όμοιες σημειακές πηγές Π1 και Π2 που απέχουν μεταξύ τους απόσταση d. Οι πηγές αρχίζουν να ταλαντώνονται τη χρονική στιγμή t = 0 και εκτελούν ταλαντώσεις της
μορφής  y = A ∙ ημωt  δημιουργώντας στην επιφάνεια του υγρού εγκάρσια κύματα.
Ένα υλικό σημείο Σ της επιφάνειας του υγρού που απέχει αποστάσεις r₁ = 1,4 m και r₂ (r₂ > r₁) αντίστοιχα από τις πηγές Π1 και Π2 ταλαντώνεται και η απομάκρυνσή του από τη θέση ισορροπίας του σε συνάρτηση με τον χρόνο περιγράφεται από τη γραφική παράσταση του σχήματος. 

Γ1.  Να υπολογίσετε την ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού (μονάδες 3) και την απόσταση r₂ του σημείου Σ από την πηγή Π2.                   (μονάδες 3)                Μονάδες 6  

Γ2.  Να υπολογίσετε τη συχνότητα ταλάντωσης των πηγών Π1 και Π2 (μονάδες 3) και το μήκος κύματος λ των εγκαρσίων κυμάτων που διαδίδονται στην επιφάνεια του υγρού. (μονάδες 3)                      Μονάδες 6
Γ3.  Να υπολογίσετε την απομάκρυνση του σημείου Σ από τη θέση ισορροπίας τη χρονική στιγμή  t = 5/8 s.                   Μονάδες 6
Γ4.  Μεταβάλλουμε ταυτόχρονα, με τον ίδιο τρόπο, τη συχνότητα ταλάντωσης των δύο πηγών Π1 και Π2. Να υπολογίσετε την ελάχιστη συχνότητα ταλάντωσης των δύο πηγών Π1 και Π2 ώστε το σημείο Σ να παραμένει συνεχώς ακίνητο, μετά τη συμβολή των κυμάτων στο σημείο αυτό.          Μονάδες 7

Γ1.  v = r₁ / t₁ = 1,4m / 0,35s = 4 m/s    r₂ = v t₂ = 4m/s 0,55s = 2,2 m    

Γ2.    T = (0,55s - 0,35s) / 2 = 0,1 s   f = 1/T = 10 Hz         λ = v / f = 0,4 m       ω = 2πf = 20π ad/s 

Γ3.   y₁ = 0,05 ημ(2πf t - 2πr₁ /λ) = 0,05 ημ(20πt - 2π 1,4 / 0,4) = 0,05 ημ(20πt - 7π)

 y₂ = 0,05 ημ(2πf t - 2πr₂ /λ) = 0,05 ημ(20πt - 2π 2,2 / 0,4) = 0,05 ημ(20πt - 11π)

    5/8 s = 0,625 s > 0,55 s   έχουν φθάσει και τα δύο κύματα στο σημείο Σ  

  y = 0,1 συν(11π - 7π)/2  ημ( 20πt - 18π/2 ) =  0,1 συν(2π)  ημ(20πt - 9π) =  0,1 ημ(20πt - 9π)  =  y(t)

y(5/8) = 0,1 ημ(20π 5/8 - 9π)  =  0,1 ημ(12π + π/2 - 9π)  = 0,1 ημ(π/2 + 3π)  = 0,1 ημ(3π/2) = - 0,1 m

  y(t)  =  0,1 ημ(20πt - 9π)  =>   v(t)  = 2π συν(20πt - 9π)  

  v(5/8)  = 2π συν(20π 5/8 - 9π)  =  2π  συν(12π + π/2 - 9π)  =  2π συν(3π/2) = 0

Γ4.   

 το σημείο Σ είναι ακίνητο   r₂ - r₁ = Νλ' + λ'/2  =>^Ν=0    2,2 - 1,4 =  λ'/2  =>  λ' = 1,6 m  

  f ' = v / λ' = 4m/s / 1,6m = 2,5 Hz    

επαναληπτικές  ΣΕΠ 2016

Β2.  Εγκάρσιο αρμονικό κύμα διαδίδεται χωρίς απώλειες ενέργειας σε γραμμικό ελαστικό μέσο που ταυτίζεται με τον
άξονα x ́Οx προς τη θετική κατεύθυνση.
Η πηγή του κύματος βρίσκεται στην αρχή Ο του άξονα x ́Οx και εκτελεί απλή αρμονική ταλάντωση με εξίσωση
y = Αημωt.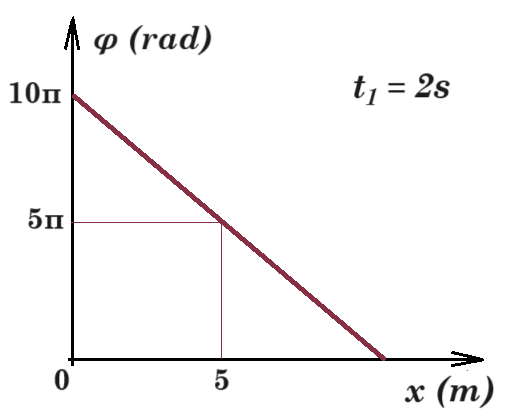 

Στο διάγραμμα του σχήματος  παριστάνεται η φάση των σημείων του ελαστικού μέσου σε συνάρτηση με την απόστασή τους x από την πηγή, τη χρονική στιγμή t₁ = 2s. Η ταχύτητα διάδοσης του κύματος είναι ίση με:
i.  υ = 0,8 m/s                 ii.  υ = 5 m/s                iii.  υ = 12,5 m/s

  φ  =  ωt  -  2πx / λ           φ = 10π - πx    [0 , 10m]              

   10π rad  =  ω 2s  =>  ω = 5π rad/s        T = 2π/ω = 2π / 5π = 0,4 s        

   2π / λ = π  =>   λ = 2 m           v =  λ / T =  2m /0,4s  = 5 m/s      (ii)