ΘΕΜΑ Γ   22

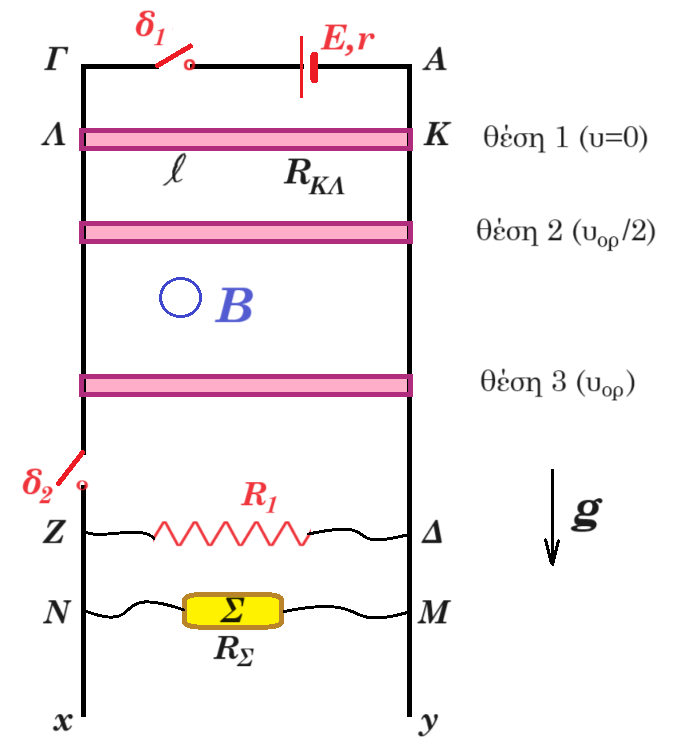
Οι μεγάλου μήκους, κατακόρυφοι, μεταλλικοί αγωγοί Αx και Γy απέχουν μεταξύ τους σταθερή απόσταση l = 1 m και έχουν αμελητέα ωμική αντίσταση.  Στα άκρα Α, Γ συνδέεται πηγή ηλεκτρεγερτικής δύναμης Ε = 9 V και εσωτερικής αντίστασης r = 1 Ω.  
Αγωγός ΚΛ μήκους l = 1 m, μάζας m = 0,3 kg και ωμικής αντίστασης R_ΚΛ = 2 Ω έχει τα άκρα του Κ, Λ πάνω στους κατακόρυφους αγωγούς Αx και Γy, είναι κάθετος σε αυτούς και είναι δυνατόν να ολισθαίνει κατά μήκος των αγωγών χωρίς τριβές. 
Η όλη διάταξη βρίσκεται σε περιοχή που υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης B, του οποίου οι δυναμικές γραμμές είναι κάθετες στο επίπεδο του σχήματος.

Αρχικά ο διακόπτης δ₁ είναι κλειστός, ο διακόπτης δ₂ είναι ανοικτός και ο αγωγός ΚΛ είναι ακίνητος στη θέση 1.
Γ1.  Να υπολογίσετε το μέτρο Β της έντασης του μαγνητικού πεδίου (μονάδες 3) και να προσδιορίσετε την κατεύθυνσή της. (μονάδα 1)            Μονάδες 4

Στο κάτω μέρος της διάταξης, μεταξύ των σημείων Ζ και Δ, είναι συνδεδεμένος αντιστάτης με ωμική αντίσταση R₁ = 3 Ω και στα σημεία Μ, Ν είναι συνδεδεμένη θερμική συσκευή Σ ωμικής αντίστασης R_Σ, η οποία όταν στα άκρα της Μ, Ν έχει τάση ίση με 6 V λειτουργεί κανονικά αποδίδοντας θερμική ισχύ 6 W.
Ανοίγουμε τον διακόπτη δ₁, κλείνοντας ταυτόχρονα τον διακόπτη δ₂ και ο αγωγός ΚΛ αρχίζει να κατέρχεται παραμένοντας συνεχώς οριζόντιος χωρίς τα άκρα του Κ, Λ να χάνουν την επαφή με τους αγωγούς Αx και Γy.
Γ2.  Έστω ότι ο αγωγός ΚΛ έχει αποκτήσει οριακή ταχύτητα u_ορ στη θέση 3.
Να δικαιολογήσετε το είδος της κίνησης που εκτελεί ο αγωγός ΚΛ από τη θέση 1 έως τη θέση 3 (μονάδες 3) και να υπολογίσετε τη σταθερή οριακή ταχύτητα u_ορ. (μονάδες 6)          Μονάδες 9
Γ3.  Να υπολογίσετε τον ρυθμό μεταβολής της ορμής του αγωγού στη θέση 2, στην οποία η ταχύτητά του είναι ίση με  u_ορ/2.        Μονάδες 6
Γ4.  Όταν ο αγωγός έχει αποκτήσει την οριακή του ταχύτητα, να εξετάσετε αν η θερμική συσκευή Σ λειτουργεί κανονικά.      Μονάδες 6       

   Δίνεται η επιτάχυνση της βαρύτητας: g = 10 m/s²     Η αντίσταση του αέρα θεωρείται αμελητέα.

  ΣΕΠ 2023

 ΘΕΜΑ Γ
Η μεταλλική ράβδος ΟΑ περιστρέφεται κατά τη φορά περιστροφής των δεικτών του ρολογιού με σταθερή γωνιακή ταχύτητα ω μέτρου ω = 2 rad/s σε οριζόντιο επίπεδο γύρω από κατακόρυφο άξονα που διέρχεται από το άκρο της Ο. Κατά τη διάρκεια της περιστροφής ο αγωγός εφάπτεται σε κυκλικούς αγώγιμους οδηγούς ακτίνων (ΟΑ) = ℓ1 = 0,4 m και (ΟΓ) = ℓ2 = 0,2 m. Οι κυκλικοί οδηγοί, τα σύρματα σύνδεσης και ο αγωγός ΟΑ έχουν αμελητέα ωμική αντίσταση.
Ο διακόπτης (δ) αρχικά είναι ανοιχτός. Το μέτρο της έντασης του ομογενούς μαγνητικού πεδίου είναι ίσο με Β = 1 Τ και η φορά της από τον αναγνώστη προς τη σελίδα.

Γ1.  Να αποδείξετε ότι η τάση VΑΓ μεταξύ των σημείων επαφής Α, Γ του περιστρεφόμενου  αγωγού με τους κυκλικούς οδηγούς είναι ίση με VΑΓ = 0,12 V.        Μονάδες 6
Μεταξύ των άκρων Ζ και Η των κυκλικών οδηγών, παρεμβάλλεται το κύκλωμα του παραπάνω σχήματος, το οποίο βρίσκεται έξω από το ομογενές μαγνητικό πεδίο.
Το κύκλωμα περιλαμβάνει πηνίο που έχει συντελεστή αυτεπαγωγής L = 0,2 Η και ωμική αντίσταση R1 = 1,2 Ω. Ο αντιστάτης R2 έχει ωμική αντίσταση R2 = 0,6 Ω.
Γ2.  Κάποια στιγμή κλείνουμε τον διακόπτη (δ). Να σχεδιάσετε και να αιτιολογήσετε την πολικότητα της ΗΕΔ από αυτεπαγωγή στο πηνίο.  (μονάδες 2)     Να υπολογίσετε το ρυθμό μεταβολής της έντασης του ρεύματος στο πηνίο αμέσως μετά το κλείσιμο του διακόπτη (δ). (μονάδες 4)      Μονάδες 6
Γ3.  Μετά από λίγο και ενώ ο αγωγός ΟΑ συνεχίζει να περιστρέφεται τα ρεύματα στο κύκλωμα σταθεροποιούνται. Υπολογίστε τις σταθεροποιημένες τιμές των εντάσεων των ρευμάτων.  Μονάδες 6
Γ4.  Κάποια στιγμή ανοίγουμε τον διακόπτη (δ). Να σχεδιάσετε και να αιτιολογήσετε την πολικότητα της ΗΕΔ από αυτεπαγωγή στο πηνίο.  (μονάδες 2)     Να υπολογίσετε το ρυθμό μεταβολής της έντασης του ρεύματος στο πηνίο αμέσως μετά το άνοιγμα του διακόπτη (δ); (μονάδες 2)   Να υπολογίσετε το ποσό της θερμότητας που μεταφέρεται στο περιβάλλον λόγω φαινομένου Joule στους αντιστάτες, από τη στιγμή που ανοίγει ο διακόπτης (δ) και μέχρι το ρεύμα να μηδενιστεί. (μονάδες 3)      Μονάδες 7
Θεωρείστε ότι κατά τη διάρκεια της περιστροφικής κίνησης, ο αγωγός ΟΑ βρίσκεται διαρκώς μέσα στο ομογενές μαγνητικό πεδίο και για όσο χρονικό διάστημα μελετάμε το φαινόμενο δεν φτάνει στην περιοχή του κυκλώματος.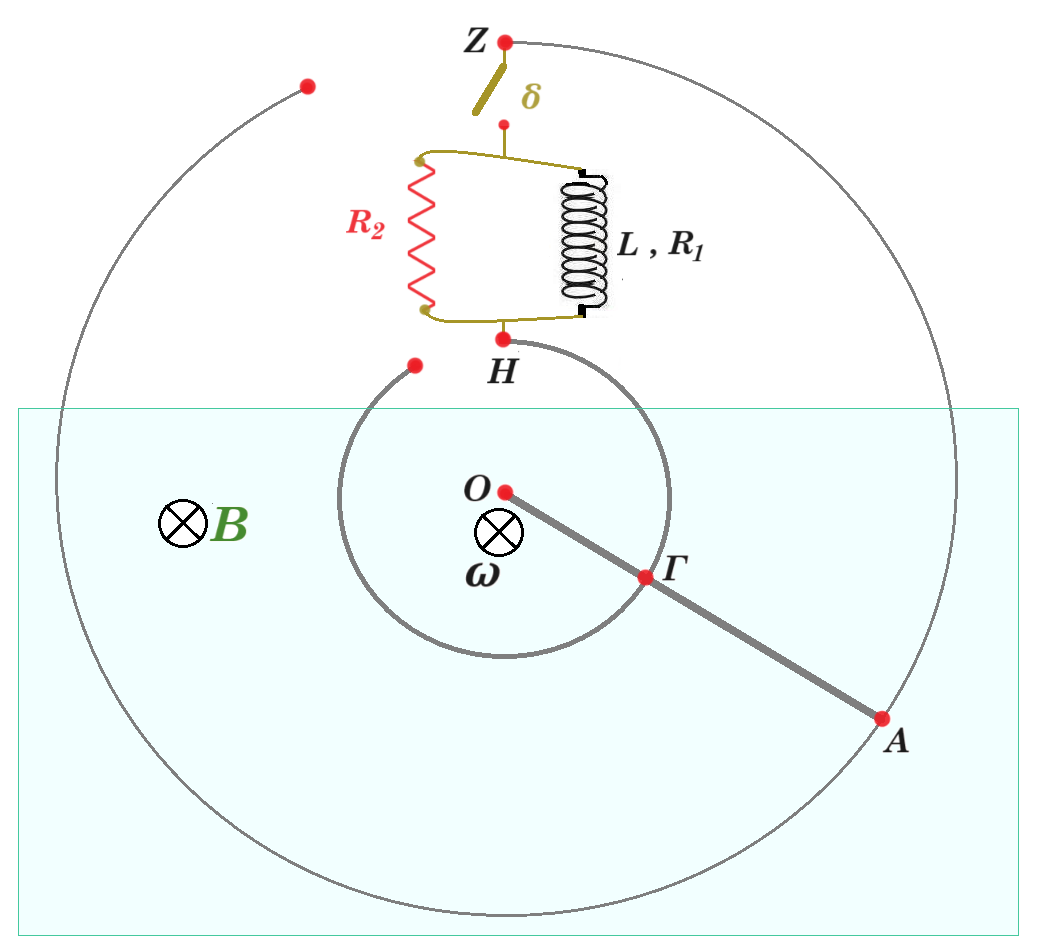

επαναληπτικές  ΣΕΠ 2023

   V_ΑΓ  =  Ε_επαγ  =  Β [ π (ΟΑ)² -  π (ΟΓ)² ] / Τ  =  Β [ π (ΟΑ)² -  π (ΟΓ)² ] / (2π/ω)  =  [ (ΟΑ)² - (ΟΓ)² ] Β ω / 2  =  ( 0,4² - 0,2² ) 1 2 / 2  =  0,16 - 0,04 = 0,12 V

  V_ZH = V_ΑΓ  =  i₂ R₂  =  L di₁/dt + i₁ R₁  =>  0,12  =  i₂  0,6  =  0,2  di₁/dt  +  i₁ 1,2   =>  i₂ = 0,12 / 0,6 = 0,2 A       σταθερό

μόλις κλείσουμε τον διακόπτη  i₁ = 0   οπότε  di₁/dt =  0,12 / 0,2 =  0,6 A/s

μετά από πολύ χρόνο :    i₂ = 0,12 / 0,6 = 0,2 A           0,12  =  - 0,2  di₁/dt  +  i₁  1,2   =>   0,12  =  i₁  1,2   =>  i₁ = 0,1 A         U_L = 0,5 L i₁²  =  0,5  0,2  0,1² = 0,001 J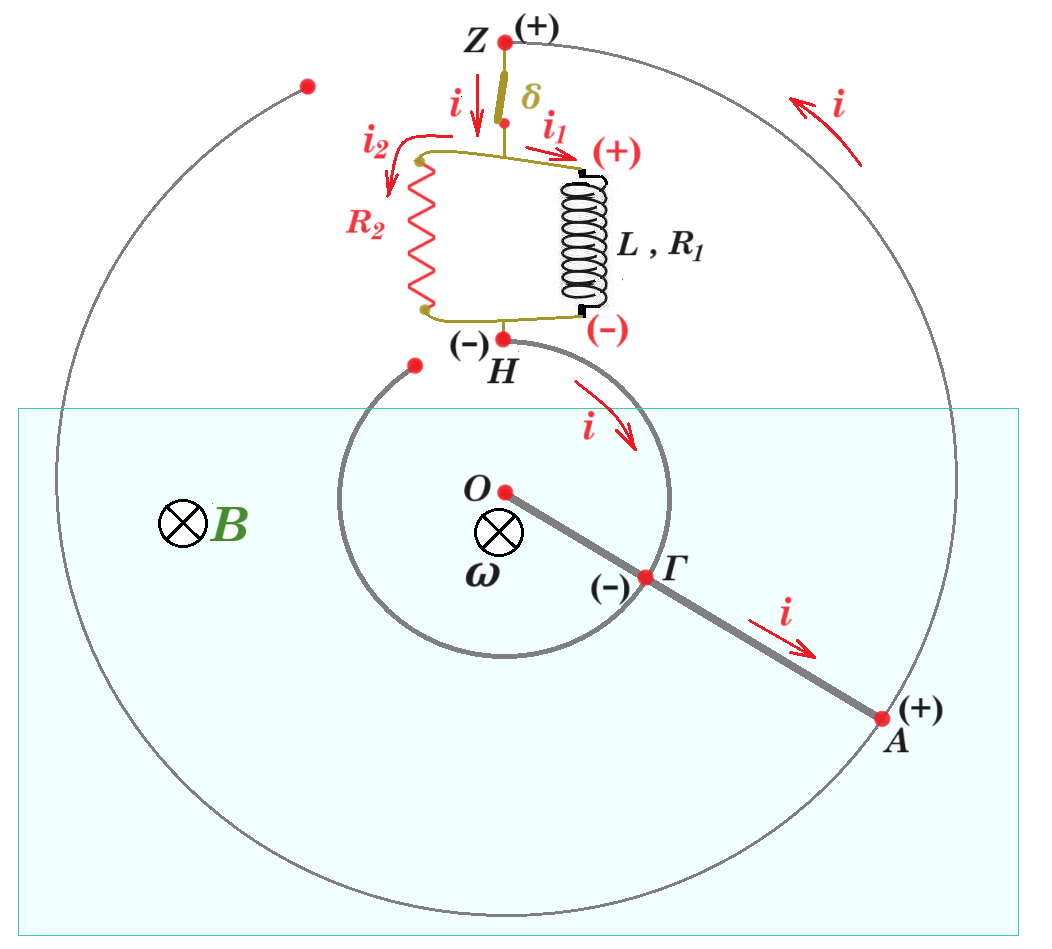 

μόλις ανοίξουμε τον διακόπτη το πηνίο διαρρέεται από i = 0,1 A  :   - L di/dt = i (R₁ + R₂)  =>  - 0,2  di/dt =  0,1  (1,2 + 0,6)  =>  di/dt = - 1,8 / 2 = - 0,9 A/s  

ΘΕΜΑ Γ   2022

Γ1.    ο δ₂  ανοικτός   ο  δ₁  κλειστός  ο αγωγός ΚΛ διαρέεται από ρεύμα  από το Λ προς το Κ  (δεξιά)   i =  E / (r + R_ΚΛ)  = 9 / (1 + 2) = 3 Α  

ο αγωγός δέχεται δύναμη Laplace  F_L = B l i 

ο αγωγός είναι ακίνητος   ΣF = 0  =>  mg - F_L = 0 =>  mg = B l i =>  B = mg / il = 3 / 3 = 1 Tesla      

η δύναμη Laplace  είναι αντίθετη του βάρους του αγωγού (προς τα πάνω)   η ένταση Β  είναι προς τα μέσα

    ωμική αντίσταση συσκευής :  R_Σ = V² / P = 6² / 6 = 6 Ω      

Γ2.    ο δ₁  ανοίγει   ο  δ₂  κλείνει    

η συσκευή συνδέεται παράλληλα με την R₁   R_1,Σ =  6 3 / (6 + 3) = 2 Ω   

ο αγωγός κατέρχεται μέσα στο μαγνητικό πεδίο  τα ηλακτρ'ονια του δέχονται δύναμη Lorentz  και κινούνται προς το άκρο Λ  που φορτίζεται αρνητικά  και το Κ  φορτίζεται θετικά    αναπτύσσεται επαγωγική τάση

  κλειστό κύκλωμα  Ε_επαγ = i ( R_ΚΛ + R_1,Σ ) =>  B l v = i ( R_ΚΛ + R_1,Σ ) =>  1 1 v = i ( 2 + 2 ) =>  v = 4i     i = v/4      

ΣF = m a  =>  mg  -  B l i  = m a  =>  3  -  v/4  = 0,3 a   (1)    καθώς η ράβδος κατέρχεται η ταχύτητά της αυξάνεται  οπότε το μέτρο της επιτάχυνσης μειώνεται   και  κάποια στιγμή μηδενίζεται  οπότε  η (1) =>  v = 12 m/s    οριακή ταχύτητα  αμέσως μετά  ( α = 0 ) η ράβδος ΚΛ κατέρχεται με σταθερή ταχύτητα  v_ορ = 12 m/s

Γ3.    θέση 2 :    v_ορ/2 = 6 m/s        i = v/4  =  6/4 = 1,5 A

   ΣF = m a  =>    ΣF =  mg  -  B l i  = m a  =>  ΣF =  3  -  1 1 1,5  = 0,3 a  =>  ΣF = dp/dt = 1,5 N  

     a = 1,5 / 0,3 = 5 m/s²

Γ4.    θέση 3  και μετά ........        i = v/4  =  12/4 = 3 A    

   V_ΚΛ = Ε_επαγ - i R_ΚΛ =  B l v_or - i R_ΚΛ =  1 1 12  -  3 2  = 6 Volt  

στα άκρα της συσκευής επικρατεί τάση  6 Volt    άρα λειτουργεί κανονικά 

η συσκευή διαρρέεται από  i_Σ = V_ΚΛ / R_Σ =  6 / 6 = 1 Α   άρα λειτουργεί κανονικά 

η αντίσταση R₁   διαρρέεται από  i₁ = V_ΚΛ / R₁ =  6 / 3 = 2 Α