

Ο αγωγός ΟΑΓ του σχήματος αποτελείται από δύο ράβδους ΟΑ και ΑΓ κάθετες μεταξύ τους με μήκη (ΟΑ) = 0,6 m και (ΑΓ) = 0,8 m. O αγωγός στρέφεται στο επίπεδο της σελίδας γύρω από το άκρο του Ο με σταθερή γωνιακή ταχύτητα μέτρου ω = 10 rad/s κάθετα στις γραμμές ομογενούς μαγνητικού πεδίου μέτρου έντασης Β = 1Τ. Η απόλυτη Η.Ε.Δ. από επαγωγή στα άκρα του αγωγού ΑΓ είναι ίση με:
α. μηδέν β. 3,2 V γ. 5 V
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
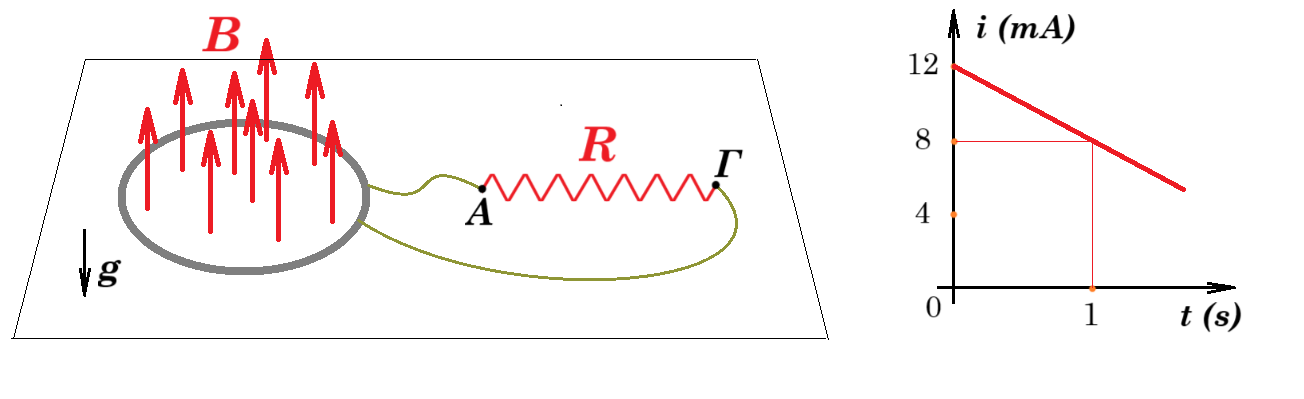
Συρμάτινο κυκλικό πλαίσιο, το οποίο αποτελείται από 10 σπείρες, με εμβαδόν κάθε σπείρας Α=0,01m2, βρίσκεται μέσα σε ομογενές μαγνητικό πεδίο με το επίπεδό του σε οριζόντιο επίπεδο, κάθετο στις δυναμικές γραμμές ενός κατακόρυφου ομογενούς μαγνητικού πεδίου έντασης Β0=1Τ. Κάποια στιγμή το μαγνητικό πεδίο αρχίζει να αυξάνεται με σταθερό ρυθμό και γίνεται Β1=2Τ σε χρόνο Δt=2s. Το πλαίσιο παρουσιάζει αντίσταση r=2Ω, ενώ τα δυο άκρα του σύρματος συνδέονται με μια αντίσταση R=3Ω.
i) Να υπολογίσετε την ένταση του ρεύματος που διαρρέει το κύκλωμα. Ποια είναι η φορά της έντασης;
ii) Να υπολογισθεί η ενέργεια του μαγνητικού πεδίου που μετατρέπεται σε ηλεκτρική ενέργεια στο κύκλωμα, στο παραπάνω χρονικό διάστημα.
iii) Να υπολογιστεί το φορτίο που πέρασε από τον αντιστάτη R, στο παραπάνω χρονικό διάστημα.
iv) Σε μια επανάληψη του πειράματος, μεταβάλλουμε κατάλληλα το μαγνητικό πεδίο, ξεκινώντας ξανά από την τιμή Β0, οπότε ο αντιστάτης R διαρρέεται από ρεύμα, με φορά από το Α στο Γ, με μεταβλητή ένταση όπως στο διάγραμμα.
α) Να υπολογιστεί ο ρυθμός μεταβολής της έντασης του μαγνητικού πεδίου τις χρονικές στιγμές t0+ και t2=1s.
β) Ποια η ένταση του μαγνητικού πεδίου τη στιγμή t2;
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Σφαίρα (Σ) μάζας m1=1kg συγκρατείται σε ύψος h=1,4m, πάνω από μια πλάκα (Π), μάζας m2=2kg, η οποία ηρεμεί στο πάνω άκρο κατακόρυφου ελατηρίου σταθεράς k=50Ν/m, όπως στο σχήμα. Θέτουμε την πλάκα σε κατακόρυφη ταλάντωση πλάτους Α και στη συνέχεια, κάποια στιγμή (tο=0) αφήνουμε ελεύθερη την σφαίρα να πέσει κατακόρυφα και να συγκρουσθεί την στιγμή t1=0,6s, με την πλάκα. Αν η κρούση μεταξύ των δύο σωμάτων είναι κεντρική και ελαστική και η σφαίρα, μετά την κρούση, αποκτά ταχύτητα προς τα πάνω μέτρου 4m/s, να βρεθούν:
α) η δυναμική ενέργεια του ελατηρίου την στιγμή της κρούσης.
β) το πλάτος Α της ταλάντωσης, πριν την κρούση.
γ) το νέο πλάτος Α' της ταλάντωσης της πλάκας, μετά την κρούση.
Δίνεται g=10m/s2.
τα ηλεκτρόνια της ράβδου ΟΑ δέχονται δύναμη Lorentz οπότε κινούνται προς το άκρο Α που φορτίζεται αρνητικά ενώ το άκρο Ο φορτίζεται θετικά
τα ηλεκτρόνια της ράβδου ΑΓ δέχονται δύναμη Lorentz οπότε κινούνται προς το άκρο Γ που φορτίζεται αρνητικά ενώ το άκρο Α φορτίζεται θετικά
VΟΓ = VOA + VΑΓ => B π(ΟΓ)2 / Τ = Β π(ΟΑ)2 / Τ + VΑΓ => Β ω/2 (ΟΓ)2 = Β ω/2 (ΟΑ)2 + VΑΓ =>
=> VΑΓ = 1Τ 10 rad/s / 2 1m2 - 1T 10 rad/s / 2 0,36m2 = 3,2 V
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
B(t) = 0,5.t + 1 (Tesla)
Εεπαγ = - ΔΦ/Δt = - A ΔΒ/Δt N = - 0,01m2 (2T - 1T)/2s 10 σπείρες = - 0,05 V = i (r + R) = i (2 + 3) => i = - 0,01 A όπως κινούνται οι δείκτες του ρολογιού Βεπαγ κατακόρυφο προς τα κάτω
Qθερμ = i2 (r + R) t = 0,012 5 2 = 0,001 J q = i t = 0,01 A 2 s = 0,02 Coulomb
i(t) = (12 - 4t) mA Εεπαγ = i (r + R) = (12 - 4t) 5 = (60 - 20t) mV
Εεπαγ = - ΔΦ/Δt = - A ΔΒ/Δt N => (60 - 20t) mV = - A ΔΒ/Δt N => (60 - 20t) mV = - 0,01 ΔΒ/Δt 10 => (60 - 20t) mV = - 0,1 ΔΒ/Δt => - (600 - 200t) mT = ΔΒ/Δt => ΔΒ/Δt = 0,2t - 0,6 (T)
t = 0+ ΔΒ/Δt = - 0,6 T/s t = 1s ΔΒ/Δt = 0,2 - 0,6 = - 0,4 T/s
t = 1s
dB/dt = 0,2t - 0,6 => dB = (0,2t - 0,6)dt => B - B0 = 0,5 0,2 t2 - 0,6 t => B = 1 + 0,1 - 0,6 = 0,5 Tesla
από το εμβαδόν του τραπεζίου θα βρούμε το φορτίο που διέρχεται από το κύκλωμα σε 1s
q = (12 + 8)mA / 2 1s = 10 mC = 0,01 Coulomb
q = Ν |ΔΦ|/(r + R) = Ν Α |ΔΒ|/(r + R) = Ν Α |Β - Β0|/(r + R) =>
=> 0,01 = 10 0,01 |Β - 1|/5 => Β = 0,5 Τ διότι μειώνεται η ένταση του μαγνητικού πεδίου επειδή για τη στιγμή t = 1s είναι ΔΒ/Δt = 0,2 - 0,6 = - 0,4 T/s
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
ισορροπία Σ2 : m2 g = k y0 => 20 = 50 y0 => y0 = 0,4 m συσπείρωση ελατηρίου
στην Θ.Ι. το ελατήριο είναι συσπειρωμένο κατά y0 = 0,4 m
α) h = 0,5 g t2 = 0,5 10 0,62 = 1,8 m v1 = g t = 10 0,6 = +6 m/s θετική προς τα κάτω
τη στιγμή t = 0,6 s η απομάκρυνση του Σ2 είναι y = 1,8 m - 1,4 m = + 0,4 m θετική προς τα κάτω
άρα το ελατήριο είναι συσπειρωμένο κατά 0,4 m + y0 = 0,8 m οπότε έχει δυναμική ενέργεια :
Uελατ = 0,5 50 N/m (0,8 m)2 => Uελατ = 16 J
β) ελαστική κρούση :
v1' = v1 (m1 - m2) / (m1 + m2) + 2 m2 v2 / (m1 + m2) =>
=> - 4 = 6 (1 - 2) / 3 + 2 2 v2 / 3 => - 4 = - 2 + 4 v2 / 3 => - 2 = + 4 v2 / 3 => v2 = - 3/2 m/s
ταλάντωση του Σ2 : ω2 = k/m2 = 50 / 2 => ω = 5 rad/s
y(t) = A ημ(5t + θ) v(t) = 5A συν(5t + θ) α(t) = - 25A ημ(5t + θ)
y(0) = A ημθ v(0) = 5A συνθ
y(0,6) = A ημ(5 0,6 + θ) = A ημ(3 + θ) = 0,4 m => Α ημ(3 + θ) = 0,4 (1)
v(0,6) = 5A συνθ = 5A συν(5 0,6 + θ) = 5A συν(3 + θ)
v2 = v(0,6) => 5A συν(3 + θ) = - 3/2 => Α συν(3 + θ) = - 0,3 (2)
(1)2 + (2)2 => Α2 = 0,42 + 0,32 = 0,52 => Α = 0,5 m
επειδή ημ3 @ ημπ = 0 και συν3 @ συνπ = - 1
έχουμε : ημ(3 + θ) = 0,4 / 0,5 = 0,8 => ημ3 συνθ + συν3 ημθ = 0,8 => ημθ = - 0,8
και συν(3 + θ) = - 0,3 / 0,5 = - 0,6 => συν3 συνθ - ημ3 ημθ = - 0,6 => συνθ = 0,6
γ) v2' = v2 (m2 - m1) / (m1 + m2) + 2 m1 v1 / (m1 + m2) =>
=> v2' = - 3/2 (2 - 1) / 3 + 2 1 6 / 3 => v2' = - 1/2 + 4 => v2' = 3,5 m/s το Σ2 μετά την κρούση κινείται προς τα κάτω με ταχύτητα 3,5 m/s και είναι σε απομάκρυνση 0,4 m από τη Θ.Ι. του οπότε
διατήρηση ενέργειας για την νέα ταλάντωση : ½ m2 (v2')2 + ½ k y2 = ½ k (A')2 =>
=> 2 3,52 + 50 0,42 = 50 (A')2 => 24,5 + 8 = 50 (A')2 => A' = √0,65 m
άλλος τρόπος :
y(t) = A' ημ(5t + φ) v(t) = 5A' συν(5t + φθ) α(t) = - 25A' ημ(5t + φ)
y(0) = A' ημφ = 0,4 (3) v(0) = 5A' συνφ = 3,5 => A' συνφ = 0.7 (4)
από (3)2 + (4)2 => (Α')2 = 0,44 + 0,72 = 0,16 + 0,49 = 0,65 => A' = √0,65 m
από (3) / (4) => εφφ = 4/7

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~