ΘΕΜΑ Γ
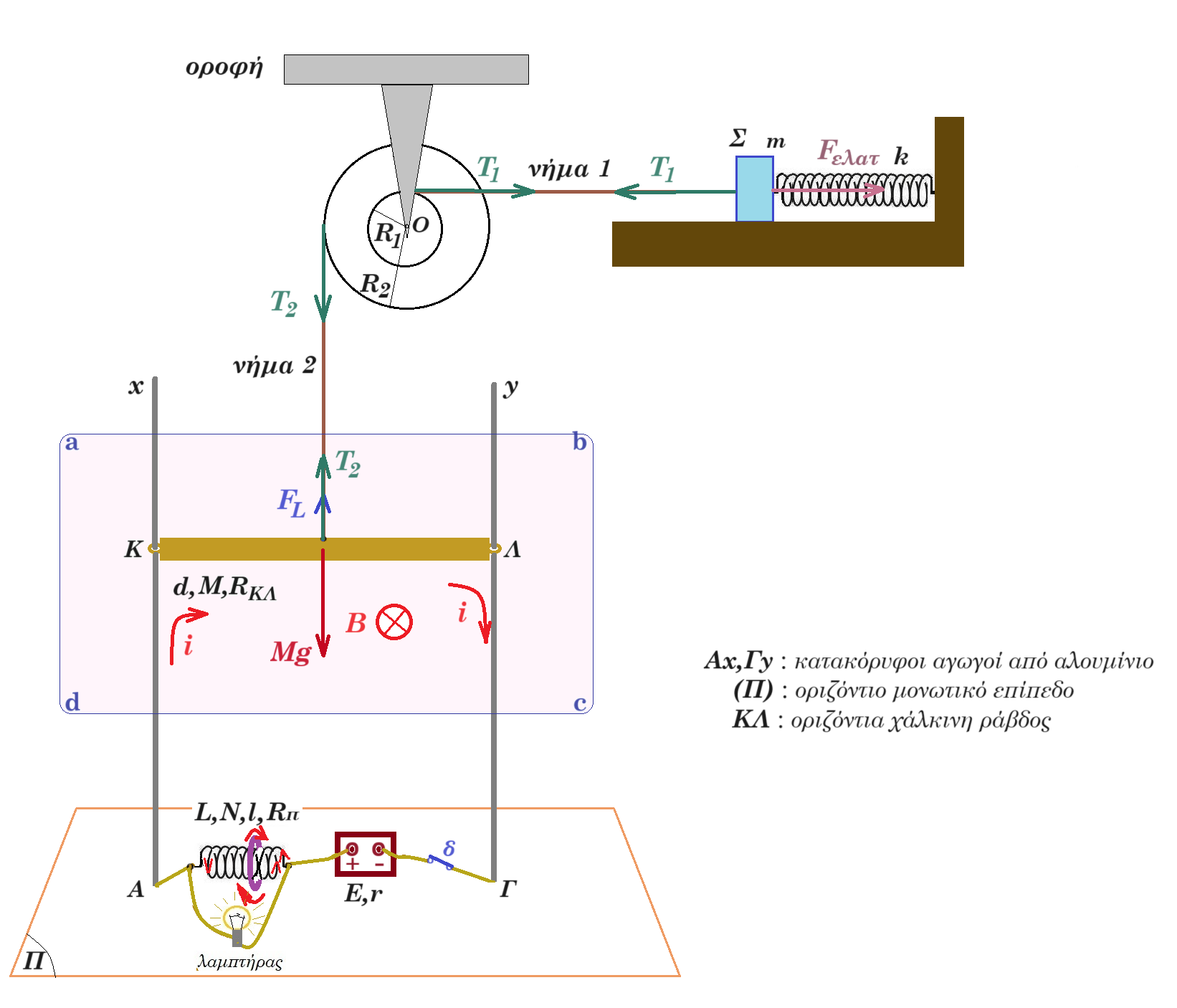
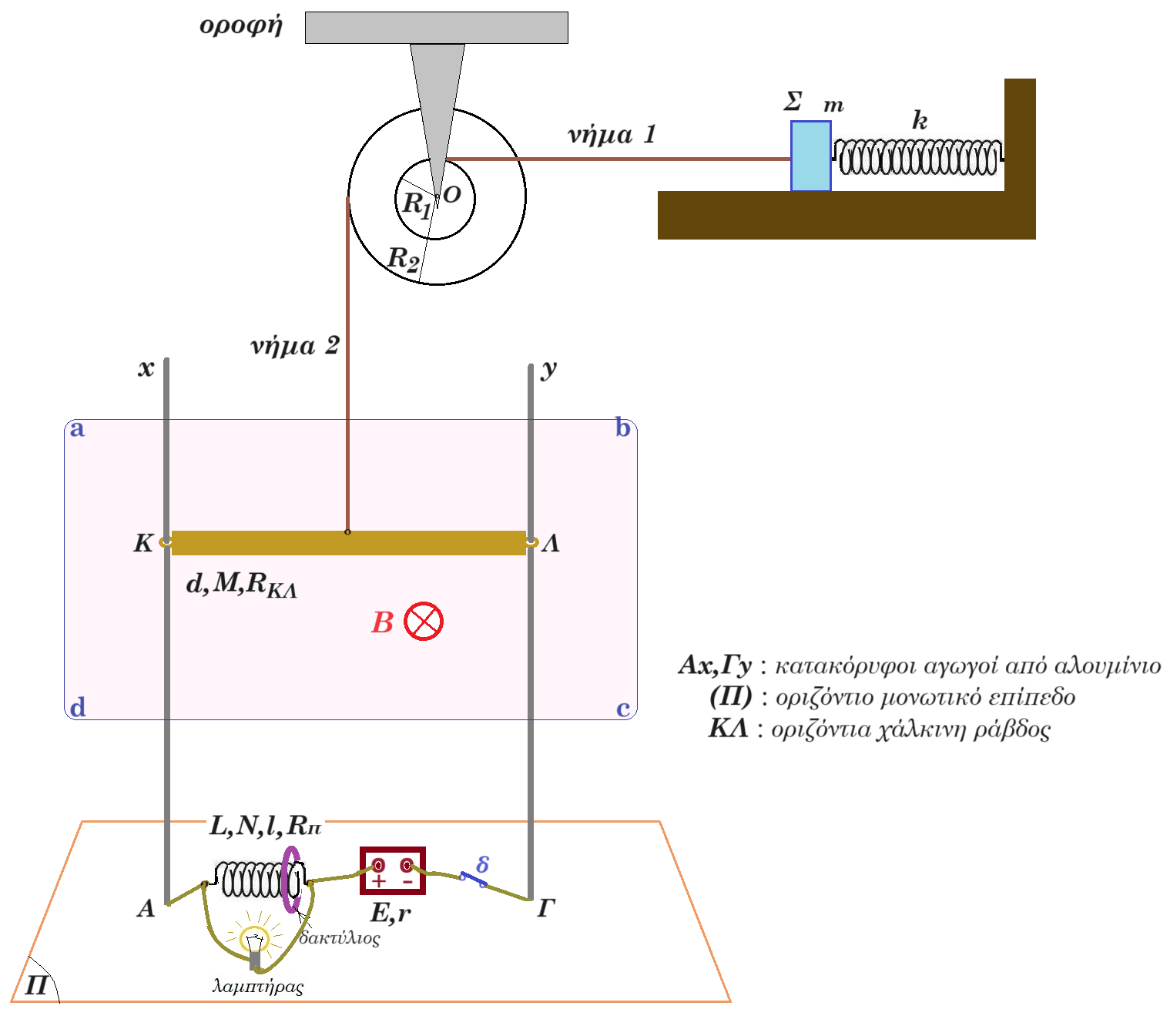
Στην κατακόρυφη διάταξη του σχήματος ο διακόπτης δ είναι κλειστός, τα σώματα βρίσκονται σε ισορροπία (ακίνητα). Το σώμα Σ έχει μάζα m = 0,6kg το ιδανικό ελατήριο έχει σταθερά k = 60 N/m η διπλή τροχαλία έχει ακτίνες R2 = 0,6m R1 = 0,2m είναι στερεωμένη στην οροφή η ράβδος ΚΛ έχει μάζα M = 0,5 kg μήκος d = 1m ωμική αντίσταση RΚΛ = 3Ω η ηλεκτρική πηγή συνεχούς ρεύματος έχει ηλεκτρεγερτική δύναμη E = 12 V εσωτερική αντίσταση r = 1 Ω το οριζόντιο ομογενές μαγνητικό πεδίο έχει ένταση B = 2/3 Tesla ο λαμπτήρας έχει ωμική αντίσταση Rλ = 12 Ω το πηνίο φέρει Ν = 100 σπείρες με εμβαδόν Απ = π.10-4 m2 για κάθε σπείρα, έχει μήκος l = 0,1 m ωμική αντίσταση Rπ = 6 Ω συντελεστή αυτεπαγωγής L = 0,18 Henry.

Γ.1. Μετακινούμε λεπτό κλειστό κυκλικό δακτύλιο που έχει ωμική αντίσταση Rδ = 1Ω και εμβαδόν επιφάνειας Αδ = 3,2.10-4 m2 από το άκρο του πηνίου έως το μέσον αυτού σε χρονικό διάστημα Δt = 1 ms. Εξηγείστε γιατί ο δακτύλιος διαρρέεται από ηλεκτρικό ρεύμα, βρείτε την ένταση του και σχεδιάστε την φορά του. μονάδες 5
Τη στιγμή t = 0 ανοίγουμε τον διακόπτη δ και αφαιρούμε το νήμα 1.
Γ.2. Εκφράστε τον ρυθμό μεταβολής της κινητικής ενέργειας του σώματος Σ συναρτήσει του χρόνου.
Σχεδιάστε τη γραφική παράσταση U(x) της δυναμικής ενέργειας του ελατηρίου συναρτήσει της απομάκρυνσης του σώματος Σ από τη θέση ισορροπίας του σε βαθμολογημένους άξονες. μονάδες 5
Εάν κατά τη διάρκεια της κίνησης του σώματος Σ ενεργεί πάνω του δύναμη F με μέτρο ανάλογο της ταχύτητάς του αλλά αντίθετης κατεύθυνσης τότε το πλάτος ταλάντωσης μειώνεται κατά 20% της αρχικής του τιμής κατά τη διάρκεια της περιόδου.
Γ.3. στο τέλος της 1ης περιόδου η δύναμη επαναφοράς έχει μέτρο ίσο με :
Α. 10 Ν Β. 6 Ν Γ. 9,6 Ν Δ. 12 Ν
στη χρονική διάρκεια της 2ης περιόδου η απώλεια ενέργειας είναι : - 0,276 J (Σ) (Λ)
Επιλέξτε και δικαιολογήστε την επιλογή σας. μονάδες 5
Γ.4. Η τροχαλία στρέφεται με γωνιακή επιτάχυνση αγων = 20/3 rad/s2 ενώ η ράβδος κατέρχεται κατακόρυφα, τα άκρα της Κ, Λ είναι παντοτε σε επαφή με τους αγωγούς Αx και Γy. Εξηγείστε γιατί φορτίζεται η ράβδος και εκφράστε την τάση VΚΛ συναρτήσει του χρόνου. μονάδες 5
Γ.5. Τη στιγμή t = 0 που ανοίγουμε τον διακόπτη δ o λαμπτήρας θα φωτοβολήσει εντονότερα; Εξηγείστε. Βρείτε τον ρυθμό μεταβολής της εντάσεως του ηλεκτρικού ρεύματος τη στιγμή t = 0. μονάδες 5
ΘΕΜΑ Γ
Ν = 100 σπείρες l = 0,1 m Rπ = 6Ω L = 0,18 Henry Rλ = 12Ω d = 1m M = 0,5kg RΚΛ = 3Ω
B = 1Tesla r = 1Ω E = 12V m = 0,6 kg k = 60 N/m R2 = 0,6 m R1 = 0,2 m
ο διακόπτης δ κλειστός
Rπ,λ = Rπ Rλ / (Rπ + Rλ) = 6Ω 12Ω / ( 6Ω + 12Ω ) = 4Ω
Ε = i ( r + Rπ,λ + RΚΛ ) => 12 = i ( 1 + 4 + 3 ) => i = 1,5A iπ = 1A iλ = 0,5A
Bπ = μ0 iπ Ν/l = 4π 10-7 Ν/Α2 1Α 100 / 0,1m = 4π 10-4 Τ στο κέντρο του πηνίου
Βπ' = 2π 10-4 Τ στο άκρο του πηνίου
μαγνητική ροή Φαρχική = Βπ' Αδ = 2π 10-4 Τ 3,2 10-4 m2 = 6,4.π 10-8 Weber
Φτελική = Βπ Απ = 4π 10-4 Τ 3,2 10-4 m2 = 12,8.π 10-8 Weber
μεταβολή μαγνητικής ροής ΔΦ = 12,8.π 10-8 Wb - 6,4.π 10-8 Wb = 6,4.π 10-8 Wb
επαγωγική τάση Εεπαγ = - ΔΦ / Δt = - 6,4.π 10-8 Wb / 10-3 s = - 6,4.π 10-5 Volt
επαγωγικό ρεύμα iεπαγ = Εεπαγ / Rδ = - 6,4.π 10-5 V / 1 Ω = - 6,4.π 10-5 Α
λόγω της φοράς του ηλεκτρικού ρεύματος που διαρρέει το πηνίο η φορά του μαγνητικού πεδίου του πηνίου έχει κατεύθυνση οριζόντια προς τα δεξιά
από το άκρον του πηνίου έως το μέσον του η ένταση Βπ αυξάνεται οπότε ο δακτύλιος αντιδρά και διαρρέεται από επαγωγικό ρεύμα τέτοιας φοράς που το μαγνητικό πεδίο Βεπαγ που δημιουργεί τείνει να αναιρέσει την αύξηση του Βπ η κατεύθυνση του Βεπαγ είναι οριζόντια προς τα αριστερά
FL = B i d = 2/3T 1,5A 1m = 1 N δύναμη Laplace κατακόρυφη προς τα πάνω
βάρος ράβδου M g = 0,5 kg 10 m/s2 = 5 N κατακόρυφη προς τα κάτω
τάση νήματος Τ2 = 4 Ν κατακόρυφη προς τα πάνω
ισορροπία τροχαλίας Στ(Ο) = 0 => Τ2 R2 - T1 R1 = 0 => 4 0,6 - T1 0,2 = 0 => T1 = 12 N
ισορροπία Σ Τ1 = Fελατ = k Δl => 12 N = 60 N/m Δl => Δl = 0,2 m επιμήκυνση ελατηριου
ανοίγουμε τον διακόπτης δ και αφαιρούμε το νήμα 1 τη στιγμή t = 0
k = m ω2 => ω2 = k / m = 60 N/m / 0,6 kg => ω = 10 rad/s T = 2π/ω = 2π/10 = π/5 s
x(t) = 0,2 ημ(10.t + π/2) v(t) = 2 συν(10.t + π/2) a(t) = - 20 ημ(10.t + π/2)
dK/dt = m v a = 0,6 2 συν(10.t + π/2) [ - 20 ημ(10.t + π/2) ] =
= - 24 ημ(10.t + π/2) συν(10.t + π/2) = - 12 ημ(20.t + π) = + 12 ημ(20.t)
Uελατ = ½ k x2 = 0,5 60 x2 = 30 x2 - 0,2 m £ x £ + 0,2 m
= ½ 60 0,04 ημ2(10.t + π/2) = 1,2 [ 1 - συν(20.t + π) ] / 2 = 0,6 συν(20.t)
T1 = 2π/20 = π/10 s
α. στο τέλος της 1ης περιόδου η δύναμη επαναφοράς έχει μέτρο ίσο με :
Α. 10 Ν Β. 6 Ν Γ. 9,6 Ν Δ. 12 Ν
Fεπαν = - k A1 = - k 80% A0 = - 60 N/m 0,8 0,2 m = - 9,6 N
β. στη χρονική διάρκεια της 2ης περιόδου η απώλεια ενέργειας είναι :
A0 = 0,2 m A1 = 0,8 0,2 m = 0,16 m A2 = 0,8 0,16 m = 0,128 m A3 = 0,8 0,128 m = 0,1024 m
E0 = 0,5 k A02 = 0,5 60 0,22 = 1,2 J E1 = 0,5 60 0,162 = 0,768 J E2 = 0,5 60 0,1282 = 0,49152 J
ΔΕ = Ε1 - Ε0 = - 0,432 J E2 - E1 = 0,49152 J - 0,768 J = - 0,27648 J
γ. στο τέλος της 3ης περιόδου η δύναμη του ελατηρίου έχει μέτρο ίσο με :
F = 60 N/m 0,1024 m = 6,144 N
η τροχαλία στρέφεται με γωνιακή επιτάχυνση αγων = 20/3 rad/s2 και η ράβδος κατέρχεται με επιτάχυνση α = αγων R2 = 20/3 rad/s2 0,6 m = 4 m/s2 v = a t = 4.t
Eεπαγ = Β v d = 2/3T 4.t 1m = 8/3.t = VΛΚ(t) VΚΛ(t) = - 8/3.t
όταν ο διακόπτης ήταν κλειστός ο λαμπτήρας διαρρεόταν από ρεύμα iλ = 0,5 A και το πηνίο από ρεύμα iπ = 1 A , ενώ τη στιγμή που ανοίγουμε τον διακόπτη το πηνίο διαρρέεται από ρεύμα iπ = 1 A άρα ο λαμπτήρας διαρρέεται από ρεύμα i = 1 A συνεπώς φωτοβολεί εντονότερα στιγμιαία και μετά αμυδρότερα και σβήνει
- L di/dt = i (Rπ + Rλ) => di/i = - L/(Rπ + Rλ) dt => i(t) = I0 e- L/(Rπ + Rλ).t = 1 e- 0,18/18.t = e-t/100
- L di/dt = i (Rπ + Rλ) => - 0,18 di/dt = 1 (6 + 12) => di/dt = 18 / (- 0,18) => di/dt = - 100 A/s