ΠΡΟΣΟΜΟΙΩΣΗ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ

ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΨΥΧΙΚΟΥ

ΤΑΞΗ :  Γ' ΛΥΚΕΙΟΥ
ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ :   ΦΥΣΙΚΗ

ΗΜΕΡΟΜΗΝΙΑ :     /   / 2025                  Ονοματεπώνυμο : 

                                                                  ΘΈΜΑΤΑ

ΘΈΜΑ Α.

Α1.   Σώμα εκτελεί ΑΑΤ, δίνεται το διάγραμμα υ(t) της ταχύτητας συναρτήσει του χρόνου.

Η εξίσωση της απομάκρυνσης  συναρτήσει του χρόνου είναι :
  (α)  x(t) = 10 ημ(π/4 t + π/2)             (β)  x(t) = 40 ημ(π/4 t + π/2)  
  (γ)  x(t) = 40 ημ(π/4 t + 3π/2)           (δ)  τίποτα από αυτά              
                                                                                                                 μονάδες 5
Α2.  
α)  στο κέντρο Ο του κυκλικού βρόχου η ένταση του μαγνητικού πεδίου έχει μέτρο ανάλογο της γωνίας φ  και για το ευθύγραμμο σύρμα, στο εσωτερικό του το πεδίο είναι αντιστρόφως ανάλογο της απόστασης r.   
β)  στο κέντρο Ο του κυκλικού βρόχου η ένταση του μαγνητικού πεδίου είναι κάθετη στο επίπεδο της σελίδας με φορά προς την σελίδα και για το ευθύγραμμο σύρμα, στο εξωτερικό του το πεδίο είναι ανάλογο της απόστασης r. 
γ)  στο εσωτερικό του ευθυγράμμου σύρματος  η ένταση του μαγνητικού πεδίου έχει μέτρο αντιστρόφως ανάλογο της απόστασης r  και  στο εξωτερικό του το πεδίο είναι  ανάλογο της απόστασης r.   
δ)  στο κέντρο Ο του κυκλικού βρόχου η ένταση του μαγνητικού πεδίου έχει μέτρο ανάλογο της γωνίας φ, για το ευθύγραμμο σύρμα στο εσωτερικό του το πεδίο είναι ανάλογο της απόστασης r.              
                                                                                                                 μονάδες 5
Α3. 
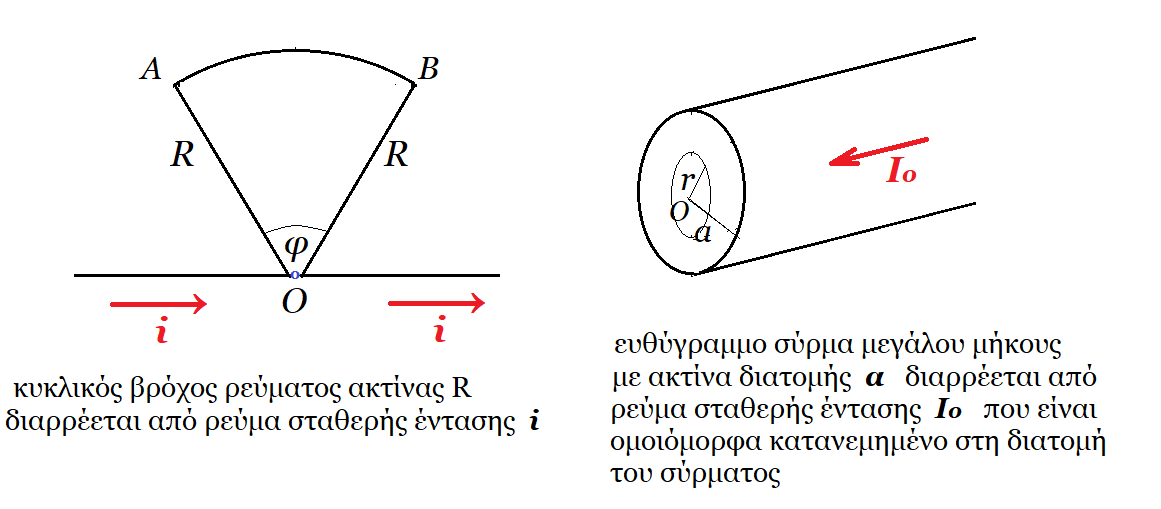
Στο κύκλωμα του σχήματος  μια ηλεκτρική πηγή συνεχούς ρεύματος συνδέεται με μεταβλητή αντίσταση (ροοστάτης)  και δύο κλάδους παράλληλους.  Ο ένας κλάδος περιλαμβάνει λαμπτήρα με ωμική αντίσταση RΛ και ο άλλος πηνίο με ωμική αντίσταση Rπ  ( RΛ > Rπ ).  Ο διακόπτης  δ  είναι κλειστός. 

α)   Μετακινούμε τον δρομέα από το άκρο Α  του ροοστάτη προς το άκρο Γ  σε χρονικό διάστημα Δt  το πηνίο  "αντιδρά"  και το άκρο του  Λ  γίνεται βόρειος πόλος        (Σ)  ή  (Λ) 

β)   Τοποθετούμε τον δρομέα σε ορισμένη θέση έτσι ώστε ο λαμπτήρας να φωτοβολεί ελάχιστα και ανοίγουμε τον διακόπτη 

    i)    ο λαμπτήρας σβήνει αμέσως

    ii)   ο λαμπτήρας φωτοβολεί αμυδρά για μικρό χρονικό διάστημα και μετά σβήνει

    iii)  ο λαμπτήρας αρχικά φωτοβολεί πιο έντονα  και μετά σβήνει

    iv)  τίποτα από τα ανωτέρω.

                                                                                                                 μονάδες  2 + 3

Α4.   Οι διπλοί αστέρες, είναι αστέρες  οι οποίοι λόγω της βαρύτητάς τους, περιστρέφονται γύρω από ένα κοινό κέντρο μάζας.  Ο μεγαλύτερος αστέρας ονομάζεται πρωτεύοντας ή κύριος ενώ ο άλλος, συνήθως μικρότερος, ονομάζεται συνοδός ή δευτερεύων αστέρας.  Έστω ο αστέρας Α  έχει μάζα Μ1  ενώ ο αστέρας Β έχει μάζα Μ2 = ½ Μ1  και περιστρέφονται γύρω από το κοινό κέντρο μάζας τους Ο.  Τα κέντρα μάζας τους απέχουν από το Ο αποστάσεις r1 , r2  αντίστοιχα.  Θεωρούμε ότι περιστρέφονται με σταθερή συχνότητα f  γύρω από το Ο  και  τα μέτρα των στροφορμών τους είναι αντίστοιχα  L1 , L2.  Κάθε σώμα ανάλογα την θερμοκρασία που έχει εκπέμπει "θερμική ακτινοβολία".  Ένας αστέρας φαίνεται ερυθρός διότι εκπέμπει στο ερυθρό του ορατού φάσματος της ακτινοβολίας. Ένας αστέρας φαίνεται κυανούς διότι εκπέμπει στο κυανού του ορατού φάσματος της ακτινοβολίας. Έστω ότι ο αστέρας Α φαίνεται ερυθρός  και  ο αστέρας Β  φαίνεται κυανούς.
 
(α)  Ο αστέρας Α έχει υψηλότερη θερμοκρασία στην επιφάνειά του απ' ότι ο αστέρας Β και ισχύει L1 = L2. 
(β)  Ο αστέρας Β έχει την ίδια θερμοκρασία στην επιφάνειά του όπως ο αστέρας Α και ισχύει  2 L1 = L2.
(γ)  Ο αστέρας Α έχει υψηλότερη θερμοκρασία στην επιφάνειά του απ' ότι ο αστέρας Β και ισχύει  L1 = 2 L2.
(δ)  Ο αστέρας Β έχει υψηλότερη θερμοκρασία στην επιφάνειά του απ' ότι ο αστέρας Α και ισχύει  2 L1 = L2.
                                                                                                                 μονάδες 5

Α5.   Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα την λέξη Σωστό, για την σωστή πρόταση, και την λέξη Λάθος, για την λανθασμένη.

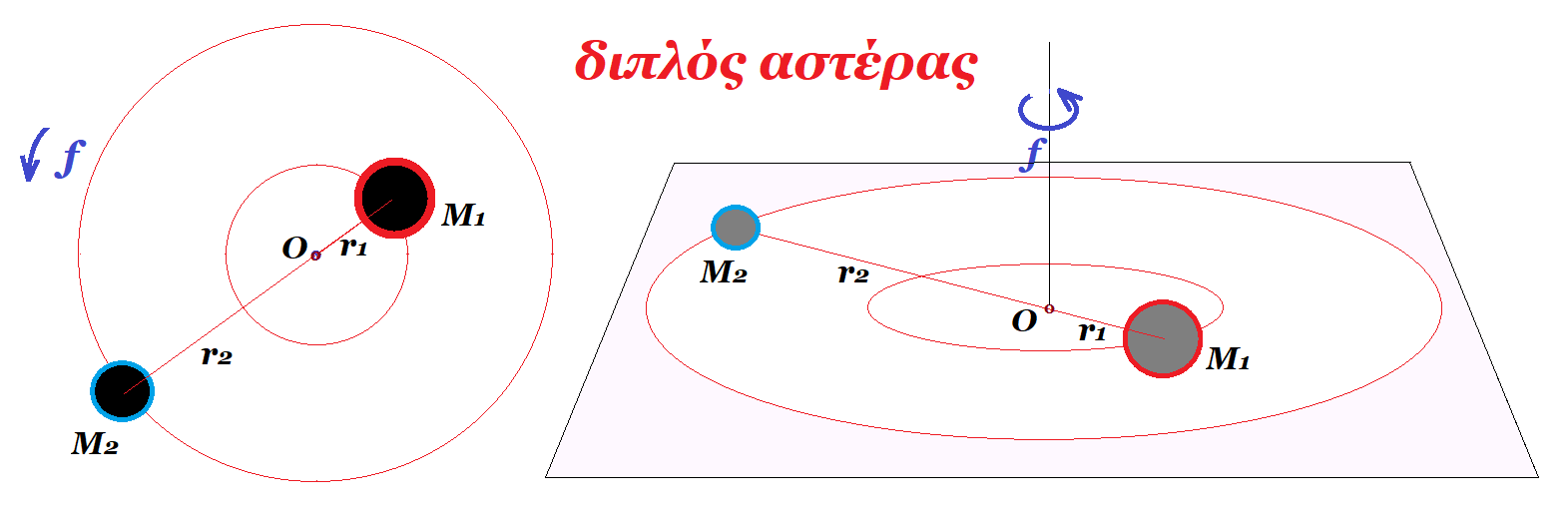
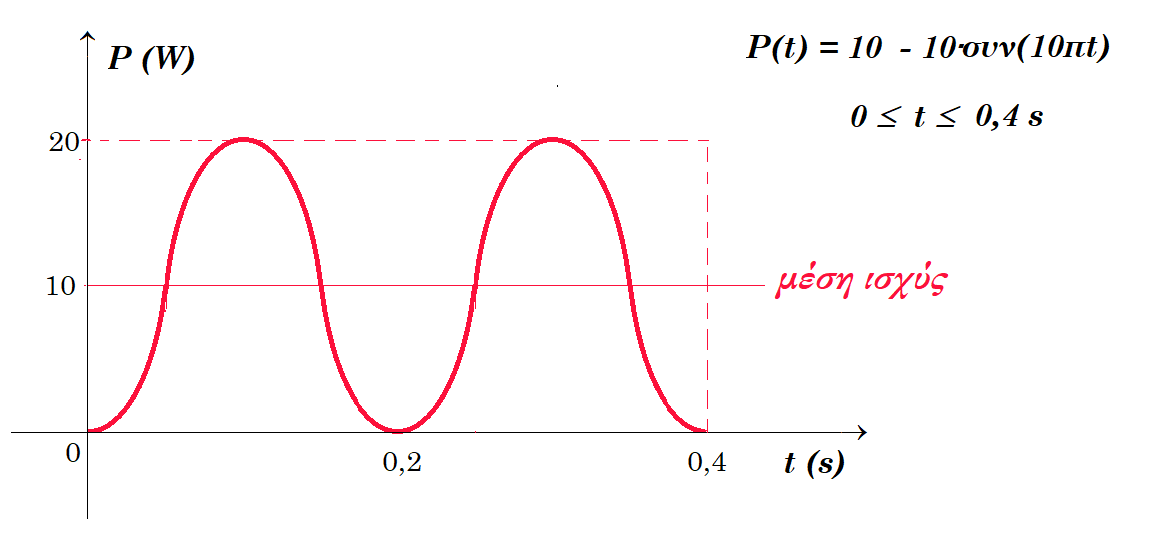
α.  Στα άκρα αντίστασης 10 Ω εφαρμόζεται εναλλασσόμενη τάση.  Η ισχύς που καταναλώνεται στην αντίσταση φαίνεται στο διάγραμμα P(t).  H ένταση του ρεύματος συναρτήσει του χρόνου είναι :  i(t) = 2∙ημ(5πt).

β.  Μεταλλική σφαίρα αμελητέας ακτίνας φέρει ηλεκτρικό φορτίο  - 17∙10-19 C.

γ.  Ο νόμος του Ampere ισχύει όταν τα ηλεκτρικά ρεύματα είναι εναλλασσόμενα.
δ.  Σε χαμηλές θερμοκρασίες 300 Κ το μέλαν σώμα εκπέμπει στο υπέρυθρο.

ε.  Ένα ηλεκτρόνιο περιστρέφεται γύρω από συνεχώς ακίνητο πρωτόνιο με σταθερή συχνότητα περιστροφής f σε ακτίνα r.  Το διάνυσμα της στροφορμής L του ηλεκτρονίου και το διάνυσμα της έντασης Β του μαγνητικού πεδίου που δημιουργεί, είναι ομόρροπα.

                                                                                                                 μονάδες 5

 

 

ΘΈΜΑ Β.

 Β1.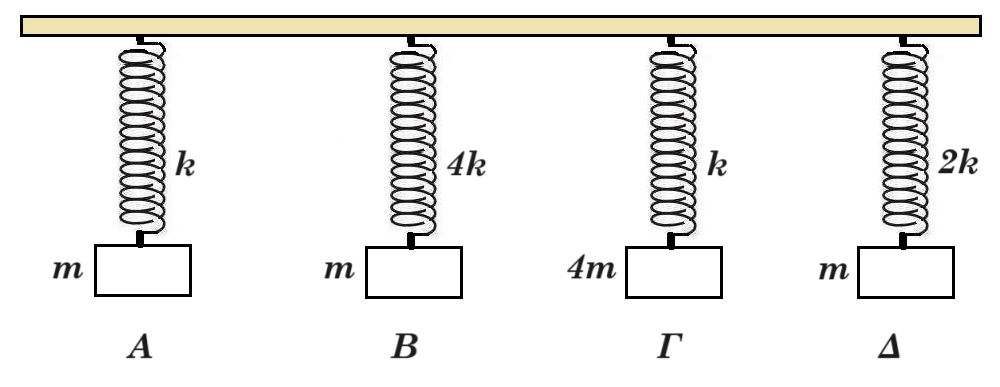

 Σε ομογενή σανίδα συνδέονται οι ταλαντωτές του σχήματος.  Διεγείρουμε την σανίδα ωστε να κάνει Α.Α.Τ. με συχνότητα  f1  Παρατηρούμε ότι τα σώματα  Α  και Γ ταλαντώνονται με το ίδιο πλάτος.

Α)  Η συχνότητα  f1  ισούται με :     α)  1/π √(k/m)      β)  1/2π √(k/2m)      γ)  1/2π √(2k/m)                  

Επιλέξτε την σωστή απάντηση.     μονάδες  1        Δικαιολογήστε την επιλογή σας.    μονάδες  4           
Β)  Ο ταλαντωτής Β  ταλαντώνεται με :   μεγαλύτερο,    μικρότερο,  ίσο    πλάτος με τον ταλαντωτή Α. 
Επιλέξτε την σωστή απάντηση.     μονάδες  1        Δικαιολογήστε την επιλογή σας.    μονάδες  4 

Β2. 

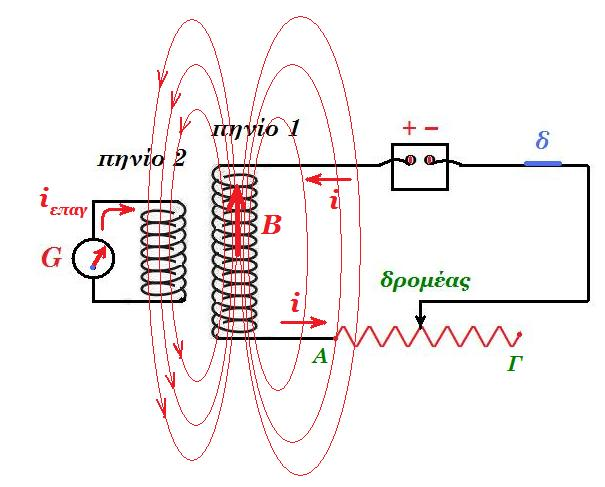Στο σχήμα ο δρομέας της μεταβλητής αντίστασης μετακινείται από το άκρο Α στο άκρο Γ. Το πηνίο 2 διαρρέεται από επαγωγικό ρεύμα όπως έχει σημειωθεί στο σχήμα.  Σωστό  ή  Λάθος.  Δικαιολογήστε την επιλογή σας.  μονάδες  1 + 6

 Β3. 

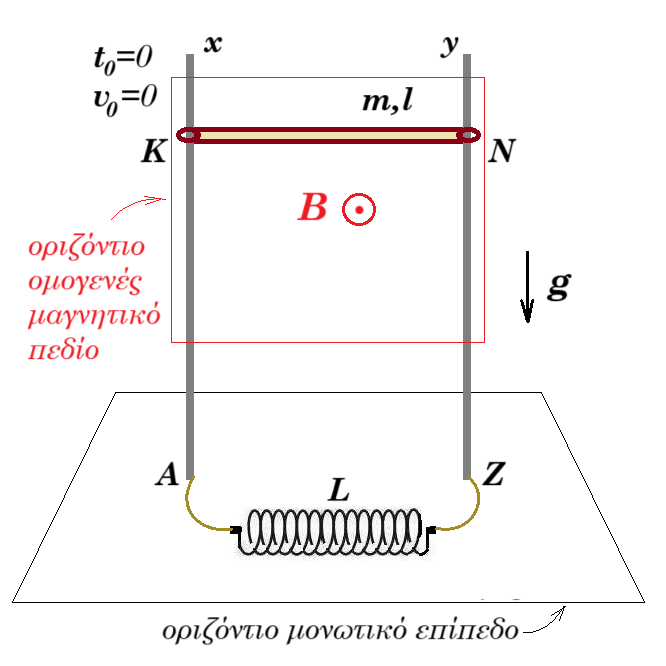Στο σχήμα η διάταξη είναι σε κατακόρυφο επίπεδο, οι αγωγοί Αx // Zy έχουν μηδενική ωμική αντίσταση, οι δυναμικές γραμμές του ομογενούς μαγνητικού πεδίου εντάσεως Β είναι οριζόντιες, το ιδανικό πηνίο με συωτελεστή αυτεπαγωγής L βρίσκεται στο οριζόντιο μονωτικό επίπεδο έξω από το πεδίο Β, συνδέεται στα άκρα Α, Ζ των αγωγών Αx και Zy,  η χάλκινη ράβδος ΚΝ, αρχικά ακίνητη, μάζας m, μήκους l, έχει μηδενική ωμική αντίσταση. Τη στιγμή t0=0 αφήνουμε την ράβδο ΚΝ ελευθερη να κινηθεί μέσα στο μαγνητικό πεδίο Β. Σε όλη την διάρκεια της κίνησής της είναι σε επαφή με του αγωγούς Αx και Zy.

 α)  η ράβδος εκτελεί επιταχυνόμενη κίνηση έως ότου αποκτήσει οριακή ταχύτητα 

 β)  η ράβδος εκτελεί απλή αρμονική ταλάντωση με συχνότητα  ω = Βl / √(mL) 

 γ)  η ράβδος εκτελεί αρχικά ομαλά επιταχυνόμενη κίνηση και μετά ομαλά επιβραδυνόμενη κίνηση μέχρι να σταματήσει    

 δ)  τίποτα από τα παραπάνω

Επιλέξτε την σωστή απάντηση.     μονάδες  1         Δικαιολογήστε την επιλογή σας.     μονάδες  7     

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ΘΈΜΑ Γ.

Η διάταξη του σχήματος βρίσκεται σε ισορροπία  (όλα είναι ακίνητα). Το σώμα Σ συνδέεται με το μέσον της ράβδου ΚΛ με νήμα αμελητέας μάζας, μη εκτατό.  Μετακινούμε το σώμα Σ σε θέση που το ελατήριο έχει το φυσικό του μήκος και αφήνουμε ελεύθερο το σύστημα να κινηθεί. 

k = 400 N/m    m=0,1kg    M=0,4kg    l=0,2m    R=2Ω    B=0,01T    r=0,2m   η μάζα της τροχαλίας είναι αμελητέα,  το βολτόμετρο είναι ιδανικό έχει άπειρη ωμική αντίσταση   

Γ1.  Μελετήστε την κίνηση των σωμάτων  και  εκφράστε την στροφορμή, ως προς το Ο, του σώματος Σ  καθώς και την ένδειξη του βολτομέτρου      Μονάδες 6              

 

Η διπλή τροχαλία μάζας Μ»0 με ακτίνες  r1 και r2 = 2r1 του σχήματος, μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από το κέντρο της Ο.  Τα νήματα (1) και (2) είναι αβαρή - μή εκτατά,  η αγώγιμη ράβδος ΚΛ (σώμα Σ1) μάζας m1=4kg,  ωμικής αντίστασης R=2Ω,  μήκους l=1m,  το σώμα Σ2 μάζας m2=1kg  είναι κολλημένο με ράβδο ΑΓ (σώμα Σ3) μάζας m3=1kg, μήκους l=1m, το οποίο συγκρατείται από κατακόρυφο ελατήριο σταθεράς k=100Ν/m. Το  σύστημα αρχικά ισορροπεί  όπως φαίνεται στο σχήμα.  Στα άκρα της η οριζόντια ράβδος ΑΓ που φέρει μικρές ακίδες απέχει από την οριζόντια επιφάνεια υγρού απόσταση  h=0,2m.

Κάποια χρονική στιγμή, την οποία θεωρούμε ως χρονική στιγμή μηδέν (t0 = 0), τα σώματα Σ2 και Σ3 αποκολλώνται και το Σ3 εκτελεί απλή αρμονική ταλάντωση κατά τη διεύθυνση της κατακορύφου.
Γ2.  Να σχεδιάσετε την γραφική παράσταση της δυναμικής ενέργειας του ελατηρίου  συναρτήσει της απομάκρυνσης από τη θέση ισορροπίας του Σ3, σε βαθμολογημένους άξονες.  Μονάδες 5

Καθώς η ράβδος ΑΓ ταλαντώνεται ακουμπούν οι ακίδες στην επιφάνεια του υγρού στα σημεία Α', Γ' οπότε δημιουργούνται εγκάρσια κύματα πλάτους Α0 που έχουν ταχύτητα διαδόσεως υδ = 2/π m/s.  Θεωρούμε σημείο Ρ της επιφάνειας του υγρού το οποίο απέχει 0,9m  και 1,1m  αντίστοιχα από τα σημεία Α' και Γ'  που είναι οι προβολές των Α και Γ.
Γ3.   α)  Να γραφεί η εξίσωση της απομάκρυνσης του σημείου Ρ σε συνάρτηση με το χρόνο.    Μονάδες 4

        β)  Βρείτε τα σημεία του ευθυγράμμου τμήματος Α'Γ' που ταλαντώνονται με μέγιστο πλάτος.   Μονάδες 4
Γ4.  Αν η τροχαλία στρέφεται με γωνιακή επιτάχυνση μετά την αποκόλληση των σωμάτων Σ2 και Σ3,  μελετήστε την κίνηση της ράβδου ΚΛ μέσα στο οριζόντιο ομογενές μαγνητικό πεδίο εντάσεως Β = 0,01 Τ.  Ποία η ένδειξη του βολτομέτρου;    Μονάδες 6
Η τριβή ανάμεσα στην τροχαλία και στα νήματα είναι αρκετά μεγάλη, ώστε να μην παρατηρείται ολίσθηση,  g=10m/s2, η ωμική αντίσταση του βολτομέτρου : RV = 99998 Ω.  

ΘΈΜΑ Δ.

H εξίσωση που περιγράφει την ένταση του ηλεκτρικού πεδίου σε ένα ηλεκτρομαγνητικό κύμα το οποίο διαδίδεται στο κενό  ή  στην ατμόσφαιρα της Γης  είναι :   Ε(x,t) = 300.ημ(2π·1018t - 2π·x/λ) (SI).
Δ1.  Να γραφεί η εξίσωση που περιγράφει την ένταση του μαγνητικού πεδίου  και  να εξεταστεί αν το κύμα αυτό ανήκει στην ορατή περιοχή του φάσματος.   μονάδες 4
Δ2.  Να σχεδιαστεί το στιγμιότυπο της έντασης του ηλεκτρικού πεδίου του κύματος τη στιγμή t=2·10-18s.   μονάδες 4

Δ3.  Το  Η/Μ κύμα προσπίπτει κάθετα σε κατακόρυφα τοποθετημένη μεταλλική επιφάνεια  στο σημείο Ο  και ανακλάται χωρίς απώλεια ενέργειας. Το ανακλώμενο κύμα δημιουργεί με το προσπίπτον, στάσιμο κύμα. Στο σημείο Ο δημιουργείται δεσμός. Πόση είναι η απόσταση μεταξύ του 2ου δεσμού και της 5ης κοιλίας του στασίμου Η/Μ κύματος.   μονάδες 3

Δ4.  Ένα φωτόνιο της ηλεκτρομαγνητικής ακτινοβολίας συχνότητας f = 1020 Hz σκεδάζεται από ακίνητο ηλεκτρόνιο. Το σκεδαζόμενο φωτόνιο κινείται κάθετα ως προς τη διεύθυνση του προσπίπτοντος φωτονίου.  Στο χώρο υπάρχει ομογενές μαγνητικό πεδίο εντάσεως Β=0,01Τ.  Να υπολογίσετε την εφαπτομένη της γωνίας που σχηματίζει η ταχύτητα του ηλεκτρονίου αμέσως μετά την σκέδαση, με τη διεύθυνση της κίνησης του αρχικού φωτονίου.  Μελετήστε την κίνηση του σκεδαζόμενου ηλεκτρονίου μέσα στο μαγνητικό πεδίο εάν η ταχύτητά του αμέσως μετά την σκέδαση σχηματίζει με τις δυναμικές γραμμές του πεδίου γωνία 45°.     μονάδες 3+3

Δ5.  Φωτίζουμε την κάθοδο στο φωτοηλεκτρικό φαινόμενο που είναι η επιφάνεια ενός μετάλλου, με "πράσινο φως"  λ = 500 nm,  ενώ υπάρχει διαφορά δυναμικού V = +1 V.  (α)  Υπολογίστε την κινητική ενέργεια ενός ηλεκτρονίου που εξέρχεται από την επιφάνεια του μετάλλου όταν φθάνει στην άνοδο.  Το έργο εξαγωγής του μετάλλου είναι 2,4 eV.   (β)  Πόση είναι η τάση αποκοπής των ηλεκτρονίων της καθόδου;   (γ)  Αν το έργο εξαγωγής του μετάλλου είναι  6,25 eV (λευκόχρυσος) πόση είναι η μέγιστη τάση μεταξύ ανόδου και καθόδου ώστε τα ηλεκτρόνια να φθάσουν με μέγιστη ταχύτητα στην άνοδο;    μονάδες 3+3+2

 h = 6,6 10-34 J.s        h / mc = 2,4 pm       c = 3 108 m/s       1 eV = 1,6 10-19 J       λ' - λ  =  h / mc (1 - συνφ) 

                             Κ α λ ή   ε π ι τ υ χ ί α !!!

 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~   

 

A2. (δ)    Βκυκλ. = 10-7 2π i/R          Biot - Savart       dB = 10-7 i dl/R2 ∙ ημ90° 
               B(O) = ΣdB = 10-7 i Σdl/R2 ∙ ημ90° = 10-7 i R φ /R2 = 10-7 i φ/R        
Α1. (δ)  Τ=8s   ω = 2π/8 = π/4 rad/s     υ(t) = - 10π συν(π/4 . t)    x(t) = - 40 ημ(π/4 . t) = 40 ημ(π/4 . t + π)
Α3. (α) (Λ)   (β) (iii)   
Α4.  (δ)
G M1 M2 / (r1 + r2)2  =  M1 v12 / r1  =  M2 v22 r2  =>  M1  ω2 r1  =  M2  ω2 r2  =>  M1  r1  =  M2  r2  =>    M1  r1  =  ½ M1  r2  =>  r1  =  ½  r2  =>   2 r1 =  r2                                
     ο κυανούς Β  εκπέμπει ακτινοβολία μεγαλύτερης συχνότητας από τον αστέρα Α   άρα μικρού μήκους κύματος  συνεπώς  έχει  υψηλότερη θερμοκρασία στην επιφάνειά του  σε σχέση με τον ερυθρό αστέρα Α    
                      διότι   λ . Τ = σταθερά       
  L1 = M1 v1 r1  =  M1 ω r12                       L2 = M2 v2 r2  =  M2 ω r22  =  ½ M1 ω  4 r12 =  2 L1        
       Μ1 >  Μ2     =>    r1 < r2    =>   L1 < L2  

 

Α5.  (β) Λ  Ν = 17∙10-19 C / 1,6∙10-19 C = 10,625 ηλεκτρόνια  ΟΧΙ ΑΚΕΡΑΙΟΣ ΑΡΙΘΜΟΣ ,   (γ) Λ,   (δ) Σ,  (ε) Λ  (α) Λ  Pμέση = iεν2 R => 10 Watt = iεν2 10 Ω  => iεν2 = 1 => iεν = 1 Α =>  i0  = √2 Α  =>  i(t) = √2 ∙ ημ(5πt)

 

      Β2.       Λ Υ Σ Η    (Σ)

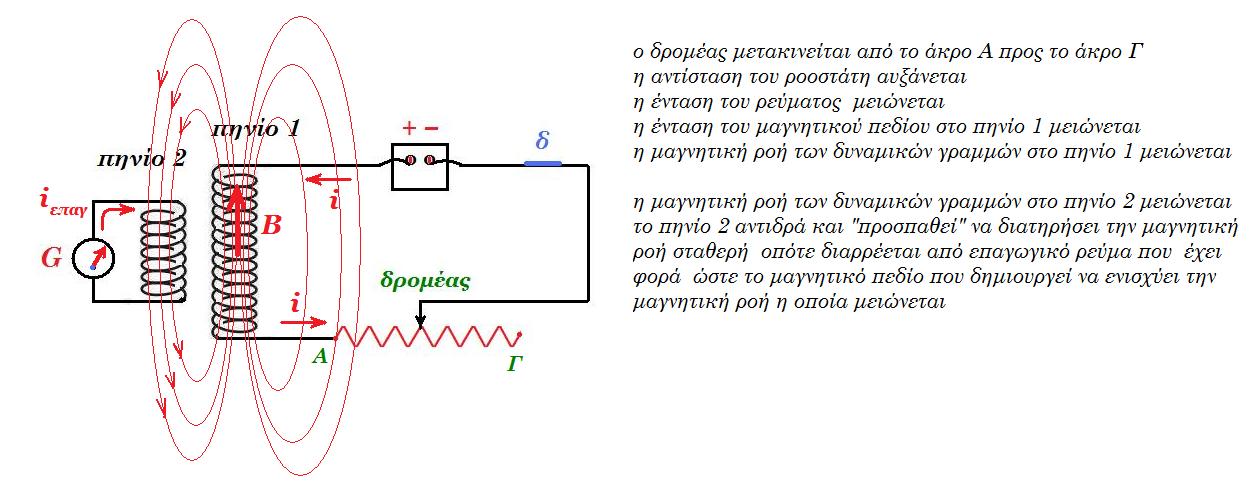     Β1.         Λ Υ Σ Η

  ωΑ2 = k/m = 4π2 fA2 k/m            ωΒ2 = 4k/m            ωΓ2 = k/4m              ωΔ2 = 2k/m    

    fA = 1/2π √(k/m)                                          fΒ = 1/2π √(4k/m)  = 1/π √(k/m)    

   fΓ = 1/2π √(k/4m)  =  1/4π √(k/m)                         fΔ = 1/2π √(2k/m)    

     fΓ = 1/2π √(k/4m)  =  1/4π √(k/m)   <   f1 = 1/2π √(k/2m)    <    fA = 1/2π √(k/m)     (β)

 

      Β3.       Λ Υ Σ Η     (β)

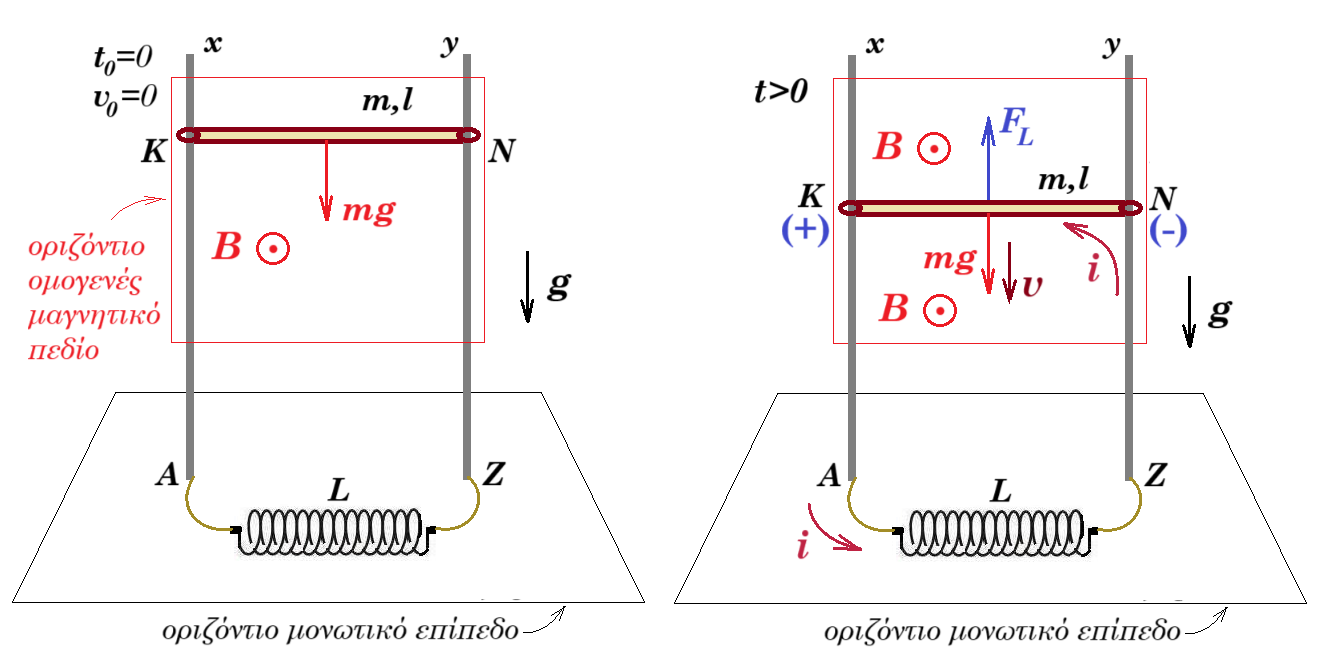
B l v  -  L di/dt  =  0    ( R = 0 )   B l  dx/dt  =  L di/dt  =>  B l x = L i  =>  i = Bl/L x   το ρεύμα ανάλογο της μετατόπισης

ΣF = m a  =>  mg -  FL  =  m a  =>  mg -  B l i  =  m a   =>  mg -  ( B2l2/ L ) ⋅ x  =  m a   =>  g - ( B2l2/ mL ) ⋅ x =  a 

  αρχικά  x = 0   =>  a = g      μετα  η  x  αυξάνεται  διότι η ράβδος κινείται προς τα κάτω   οπότε  η  α  μειώνεται  έως ότου  α = 0  =>    g = ( B2l2/ mL ) ⋅ x    =>   x = g ⋅ mL / B2l2  =  A  πλάτος ταλάντωσης της ράβδου ΚΝ   

   η ποσότητα   B2l2/ mL   είναι η  ω2  της ράβδου   ω  =  Βl / √(mL) 

 

εάν  η ράβδος κατέβει κατά   x  =  mgL / B2l2  =  A   τότε   i =  Bl/L x  =  Bl/L mgL / B2l2  =>  i  =  mg / Bl   όταν FL = mg  =>   α = 0  

διατήρηση ενέργειας   mg x  =  ½  m v2  +  ½  L i2  =>  mg   mgL / B2l2   =  ½  m v2  +  ½  L ( mg / Bl )2  => 

  =>  m2g2L / B2l2   =  ½  m v2  +  ½  L ( mg / Bl )2  =>   ½  L ( mg / Bl )2   =  ½  m v2   =>   v2  =  mL ( g / Bl )2  => 

  =>   v  = √(mL) ⋅ ( g / Bl )  =   Βl / √(mL) ⋅  g ⋅ mL / B2l2  =  ω ⋅ Α  =  vmax  μέγιστη ταχύτητα ταλάντωσης της ράβδου ΚΝ 

 

εάν  η ράβδος κατέβει κατά   2x  =  2mgL / B2l2  =  2A   τότε  i =  Bl/L ⋅ 2x  =  Bl/L ⋅ 2mgL / B2l2  =>  i  =  2mg / Bl   όταν  FL = 2mg

διατήρηση ενέργειας   mg 2x  =  ½  m v2  +  ½  L i2  =>  mg   2mgL / B2l2   =  ½  m v2  +  ½  L ( 2mg / Bl )2  => 

  =>   2m2g2L / B2l2   =  ½  m v2  +  ½  L  4 ( mg / Bl )2  =>  v = 0   η ράβδος φθάνει στο άλλο άκρο της ταλάντωσής της

....................................................................................................................................................

                           ΘΕΜΑ Γ

Γ1.   ισορροπία ράβδου ΚΛ :  Mg = T1    (1)       Τ1 = 4 Ν

 ισορροπία τροχαλίας :  Στ(Ο) = 0  =>  T2 r  -  Τ1 r  =  0  =>  T2 = T1 = Mg   (2)      Τ2 = 4 Ν 

 ισορροπία σώματος Σ :   T2  =  Fελατ =  k Δl  =>  Mg =  k Δl  =>  Δl = Mg / k  επιμήκυνση ελατηρίου         

                                     Δl =  0,4 10 / 400 =  0,01 m  = 1 cm

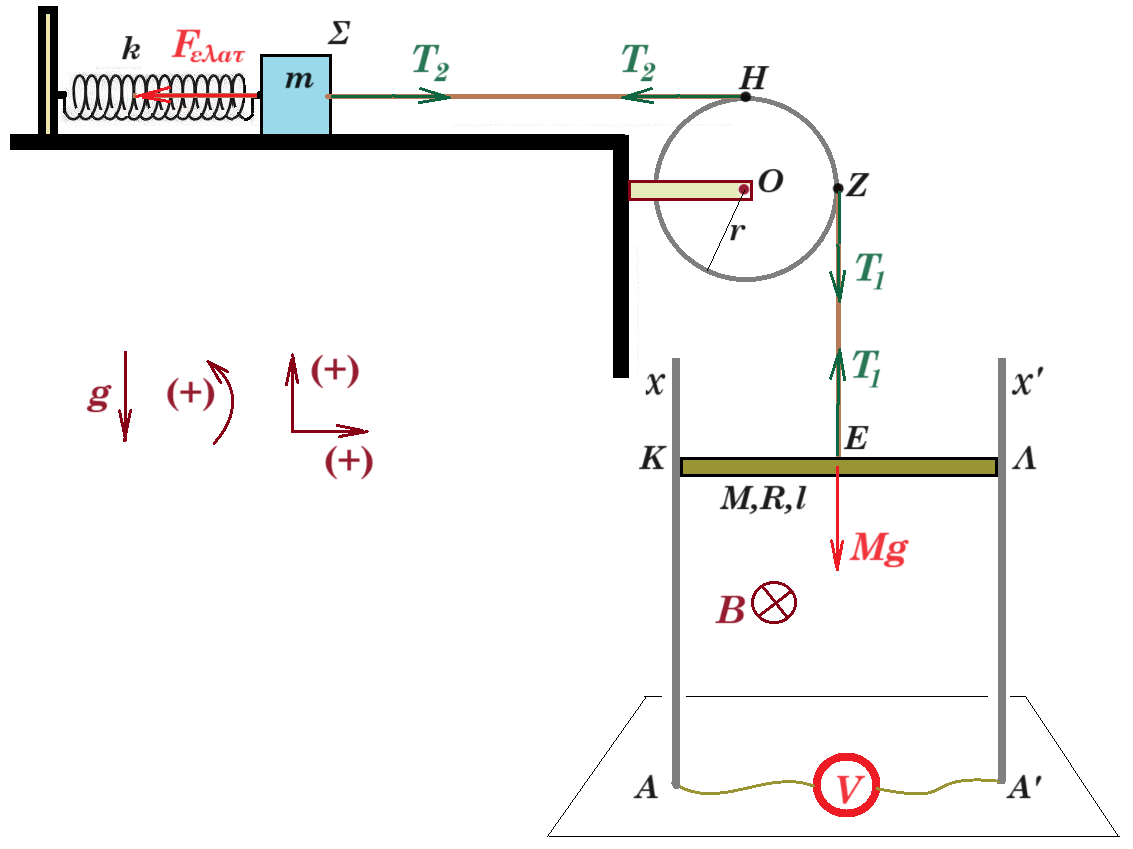
  όταν αφήσουμε το σύστημα ελεύθερο να κινηθεί,  η ράβδος ΚΛ  κινείται λόγω του βάρους της Mg,  δέχεται δύναμη Τ1  από το νήμα  οπότε το σώμα Σ  δέχεται τάση νήματος Τ2  άρα αρχίζει να κινείται  με συνέπεια να επιμηκύνεται το ελατήριο και να αποθηκεύεται σ'αυτό ενέργεια  

όσο κατεβαίνει η ράβδος ΚΛ  το έργο του βάρους της   μετατρέπεται  σε κινητική ενέργεια των σωμάτων  και  δυναμική ενέργεια ελατηρίου 

η ράβδος ΚΛ κατέρχεται με επιτάχυνση  α  η τροχαλία στρέφεται με γωνιακή επιτάχυνση  αγων = α / r  το σώμα Σ κινείται προς τα δεξιά με επιτάχυνση  α  διότι  vE = vZ = vH = vΣ     το ελατήριο επιμηκύνεται    

 

κάποια στιγμή η ράβδος ΚΛ έχει κατέβει κατά  ψ < Δl   έχοντας ταχύτητα  υ    η τροχαλία έχει στραφεί κατά γωνία θ ( ψ = θ r )  το σώμα Σ έχει μετατοπιστεί δεξιά κατά  χ = ψ < Δl   έχοντας ταχύτητα  υ    το ελατήριο έχει επιμηκυνθεί κατά χ < Δl    τη στιγμή αυτή για τη ράβδος  ισχύει :  Mg  -  Τ1  =  Μ α          για την τροχαλία : Τ1 = Τ2           για το σώμα Σ ισχύει :  Τ2  -  k χ  =  m a                   προσθέτω κατά μέλη :

Mg - T1 + T1 + T2 - k χ = M a + T2 + m a  =>  Mg - k χ = (M+m) a  =>  a > 0   διότι  Mg = k Δl > k χ   επιταχύνονται τα σώματα

 

κάποια στιγμή η ράβδος ΚΛ έχει κατέβει κατά  ψ = Δl   έχοντας ταχύτητα  υ    η τροχαλία έχει στραφεί κατά γωνία θ ( ψ = θ r )  το σώμα Σ έχει μετατοπιστεί δεξιά κατά  χ = ψ = Δl   έχοντας ταχύτητα  υ    το ελατήριο έχει επιμηκυνθεί κατά χ = Δl    

τότε   διατήρηση ενέργειας :  Mg ψ  =  ½ k ψ2  +   ½ m v2  +   ½ M v2  => 

  =>  Mg Δl  =  ½ k Δl2  +  ½ (m+Μ) v2  =>  k Δl  Δl  =  ½ k Δl2  +   ½ (m+Μ) v2  => 

  =>  ½ k Δl2  =  ½ (m+Μ) v2  =>  v2 =  Δl2  k/(m+Μ)  = Δl2 ω2  =>   v = Δl ω 

τη στιγμή αυτή για τη ράβδο ισχύει :  Mg  -  Τ1  =  Μ α              για το σώμα Σ ισχύει :  Τ2  -  k Δl  =  m a        για την τροχαλία : Τ1 = Τ2            προσθέτω κατά μέλη :

Mg - T1 + T1 + T2 - k Δl  =  M a + T2 + m a  =>  Mg - k Δl = (M+m) a  =>  a = 0   διότι  Mg = k Δl

 

αμέσως μετά η ράβδος λόγω ταχύτητας κινείται προς τα κάτω με συνέπεια το ελατήριο επιμηκύνεται περισσότερο από  Δl    άρα η δύναμη ελατηρίου είναι μεγαλύτερη από το βάρος της ράβδου  οπότε αυτή επιβραδύνεται 

κάποια στιγμή η ράβδος ΚΛ έχει κατέβει κατά  ψ > Δl   έχοντας ταχύτητα  υ    η τροχαλία έχει στραφεί κατά γωνία θ ( ψ = θ r )  το σώμα Σ έχει μετατοπιστεί δεξιά κατά  χ = ψ > Δl   έχοντας ταχύτητα  υ    το ελατήριο έχει επιμηκυνθεί κατά χ > Δl                 τη στιγμή αυτή για τη ράβδος  ισχύει :  Mg  -  Τ1  =  Μ α              για την τροχαλία : Τ1 = Τ2             για το σώμα Σ ισχύει :  Τ2  -  k χ  =  m a                 προσθέτω κατά μέλη :

Mg - T1 + T1 + T2 - k χ = M a + T2 + m a  =>  Mg - k χ = (M+m) a  =>  a < 0   διότι  Mg = k Δl < k χ   επιβραδύνονται τα σώματα

 

κάποια άλλη στιγμή το σώμα Σ και η ράβδος σταματούν να κινούνται  η ράβδος έχει κατέβει κατά  y  το Σ έχει μετατοπιστεί κατά x = y  και το ελατήριο έχει επιμήκυνση  x = y  

  τότε   διατήρηση ενέργειας :  Mg y  =  ½ k y2  =>  2 Mg / k =  y  =>  y = 2 Δl  

 

το σύστημα εκτελεί A.A.T.   με κυκλική συχνότητα  ω2 =  k/(m+Μ) =  400 / (0,1 + 0,4) = 800 =>  ω = 20√2 rad/s       και  πλάτος  Δl = 0,01 m

για το σώμα Σ :

   x = 0,01 ημ(20√2.t + 3π/2)         v = 0,2√2 συν(20√2.t + 3π/2)        α = - 8 ημ(20√2.t + 3π/2) 

για την ράβδο :

   y = 0,01 ημ(20√2.t + π/2)         v = 0,2√2 συν(20√2.t + π/2)            α = - 8 ημ(20√2.t + π/2) 

καθώς η ράβδος κινείται μέσα στο μαγνητικό πεδίο αναπτύσσεται τάση εξ' επαγωγής στα άκρα της :

   Εεπαγ = B l v =  0,01  0,2  0,2√2 συν(20√2.t + π/2)  =  0,0004√2 συν(20√2.t + π/2)          Vmax = 0,0004√2 V     

επειδή το βολτόμετρο έχει πολύ μεγάλη ωμική αντίσταση μετρά την Εεπαγ  η ένταση του ρεύματος είναι σχεδόν μηδενική  άρα  η δύναμη Laplace  είναι μηδενική  για αυτό το λόγο η ταλάντωση είναι αμείωτη

  VV = VΚΛ = 0,0004√2 συν(20√2.t + π/2)            Vmax = 0,0004√2 V    Vεν = 0,0004 V = 0,4 mV    το βολτόμετρο μετρά την ενεργό τάση

 

για την τροχαλία :  αγων = α / r  =  - 8 ημ(20√2.t + π/2)  /  0,2  = - 40 ημ(20√2.t + π/2) 

        αγων, max =  40 rad/s2    

 

L = m r v =  0,1  0,2  0,2√2 συν(20√2.t + 3π/2) =  0,004√2 συν(20√2.t + 3π/2)        Lmax = 0,004√2 kg.m2/s 

 

dK/dt  =  m v a =  0,1   0,2√2 συν(20√2.t + 3π/2)     {- 8 ημ(20√2.t + 3π/2) }  => 

          dK/dt  = - 0,16√2  συν(20√2.t + 3π/2)  ημ(20√2.t + 3π/2)  =  - 0,08√2 ημ(40√2.t + 3π) 

 

dL/dt  =  Στ(Ο)  =  ΣF  r  =  M a r  =  0,4   {- 8 ημ(20√2.t + 3π/2) }    0,2  =>  dL/dt  =  - 0,64 ημ(20√2.t + 3π/2)  

           =  -  64  0,01 ημ(20√2.t + π/2)   =>  dL/dt  =  - 64 y        [ - 0,01 m , + 0,01 m ]

 

 ...........................................................................................................................................

Γ2.   ισορροπία Σ1 :  Τ1 = m1 g = 40 N               Στ(Ο) = 0  =>  T1 r1 = T2 r2  =>  40  r1  =  Τ2  2r1  =>  T2 = 20 N

ισορροπία Σ2,3 :  Τ2 = m2,3 g +  Fελατ  =>  Τ2 = m2,3 g +  k Δl2,3 =>  20  = 20  + 100 Δl  =>  Δl2,3 = 0     το ελατήριο έχει το φυσικό του μήκος              

ισορροπία Σ3 όταν είναι μόνο του :   m3 g  =  k Δl3 =>  10  =  100 Δl3 =>  Δl3 = 0,1 m    συσπείρωση ελατηρίου   

το πλάτος ταλάντωσης του Σ3 θα είναι :  Α = Δl3 = 0,1 m   διότι αρχικά είναι ακίνητο  0,1 m υψηλότερα από τη Θ.Ι. του

κυκλική συχνότητα ταλάντωσης Σ3 :  ω2 = k / m3 = 100 / 1  => ω = 10 rad/s      f = ω / 2π = 10 / 2π = 5/π Hz  

  x(t) = 0,1 ημ(10t + π/2)        v(t) = 1 συν(10t + π/2)           a(t) = - 10 ημ(10t + π/2)  

Κ = ½ m3 v2  =  ½  1  1 συν2(10t + π/2)  =  0,5 συν2(10t + π/2)  =  0,5 { 1 + συν(20t + π) } / 2  =  0,25 +  0,25 συν(20t + π) =  0,25 - 0,25 συν(20t)

dK/dt =  m3 v a =  1  1 συν(10t + π/2)   { - 10 ημ(10t + π/2) }  = - 10 ημ(10t + π/2) συν(10t + π/2) = - 5 ημ(20t + π)  =   +5ημ(20t)      

ΣF = m3 a  =>  Fελατ  - m3 g = m3 a  =>  Fελατ - 10 = 1 { - 10 ημ(10t + π/2) }  =>  Fελατ(t) = 10  - 10 ημ(10t + π/2) 

Fελατ(x) = 10 - 100⋅x = - 100 (x - 0,1)    - 0,1 m £  x £  + 0,1 m     Fελατ(- 0,1) = 20 Ν     Fελατ(0) = 10 Ν      Fελατ(+0,1) = 0

Uελατ(x) =  0,5 100 (x - 0,1)2 =  50 (x - 0,1)2     - 0,1 m £  x £  + 0,1 m   Uελατ(- 0,1) = 2 J    Uελατ(0) = 0,5 J    Uελατ(+0,1) = 0

  

Γ2.    εγκάρσιο κύμα στην επιφάνεια του υγρού :   υδ = λ f  =>  λ = υδ / f =  (2/π) / (5/π) = 0,4 m

  x2 - x1  =  1,1 m  -  0,9 m =  0,2 m  = 0,4 m / 2  =  λ/2   το Ρ είναι ακίνητο σημείο

  y1 = A0 ημ(10t - 2πx1/λ) =  A0 ημ(10t - 2π 0,9/0,4) =  A0 ημ(10t - 4,5π)

  y2 = A0 ημ(10t - 2πx2/λ) =  A0 ημ(10t - 2π 1,1/0,4) =  A0 ημ(10t - 5,5π)

  yP = 2A0  συν(10t - 4,5π - 10t + 5,5π)/2  ημ(10t - 4,5π + 10t - 5,5π)/2  = 2A0  συν(π/2)  ημ(20t - 10π)/2 =

        =  2A0  0  ημ(10t - 5π)  =>   yP(t)  =  0            ακίνητο σημείο το Ρ

 

t1 = x1 / υδ  =  0,9 / 2/π =  9π/20 s       t2 = x2 / υδ  =  1,1 / 2/π =  11π/20 s    

[ 0 , 9π/20 s )                   yP = 0

[ 9π/20 s , 11π/20 s )     yP = A0 ημ(10t - 2πx1/λ) =  A0 ημ(10t - 2π 0,9/0,4) =  A0 ημ(10t - 4,5π)

 t  ³  11π/20 s                  yP = 0

 

Γ3.  μέγιστο πλάτος :  x1 - x2 = Nλ      x1 + x2 = 1m     2x1 = Nλ  + 1m  =>  x1 = Nλ / 2 + 0,5m  = N 0,2m + 0,5m

0 < x1 < 1m  =>  0 < N 0,2m + 0,5m  < 1m  =>  - 0,5m < N 0,2m < 0,5m  =>  - 5/2 < N < 5/2  =>  N = -2,-1,0,1,2 

  N = -2   x1 = (-2) 0,2m + 0,5m = 0,1m          x2 = 1m - 0,1m = 0,9m

  N = -1   x1 = (-1) 0,2m + 0,5m = 0,3m          x2 = 1m - 0,3m = 0,7m

  N = 0   x1 = 0,5m                                           x2 = 1m - 0,5m = 0,5m 

  N = +1  x1 = +1 0,2m + 0,5m  = 0,7m          x2 = 1m - 0,7m = 0,3m

  N = +2  x1 = +2 0,2m + 0,5m  = 0,9m          x2 = 1m - 0,9m = 0,1m

 

Γ4.   η τροχαλία στρέφεται με γωνιακή επιτάχυνση  αγων  

     a1 = αγων r1 = αγων r2/2 = a2 / 2         a2 = 2a1             

 η ράβδος κατέρχεται  με επιτάχυνση  α1   μέσα στο μαγνητικό πεδίο  τα ηλεκτρόνιά της δέχονται δύναμη Lorentz  και οδεύουν προς το άκρο Κ  το οποίο φορτίζεται αρνητικά  ενώ το άκρο Λ φορτίζεται θετικά,  έτσι αναπτύσσεται επαγωγική τάση στα άκρα Κ, Λ  Εεπαγ = Βlv, το κύκλωμα διαρρέεται από ρεύμα  i = Blv / (R+RV)    η ράβδος δέχεται δύναμη Laplace  FL = Bli = B2l2v/(R+RV)  κατακόρυφη προς τα πάνω  οπότε  ΣF = m1 a1 =>  m1 g - T1 - FL = m1 a1  =>  m1 g - T1 - B2l2v/(R+RV) = m1 a1    (1)

  Στ(Ο) = Ι(Ο) αγων   =>   T1 r1 - T2 r2 = 0   =>    T1 r1  -  T2 2r1  =  0  =>  T1 - 2T2 = 0    (2) 

 το Σ2 ανέρχεται :   Τ2 - m2 g  = m2 α2  =  m2 αγων r2   (3)

(1) + (2) + 2*(3)  =>  m1 g - T1  - B2l2v/(R+RV) + T1 - 2T2  + 2Τ2 - 2m2 g  = m1 a1 + 2m2 α2  => 

      =>   m1 g  -  B2l2v/(R+RV)  -  2m2 g  =  m1 a1  + 2m2 α2  =>    a2 = 2a1  

      =>   m1 g  -  B2l2v/(R+RV)  -  2m2 g  =  m1 a1  + 2m2 2α1  =>

      =>   (m1 - 2m2) g  -  B2l2v/(R+RV)  =  (m1 + 4m2) α1  =>

      =>   40  -  20  -  0,0001v/100000  =  8 α1  =>   20  -  v 10-9  =  8 a1     20  =  8 a1  =>  a1 = 2,5 m/s2  

     η ράβδος ΚΛ  κατέρχεται με επιτάχυνση 2,5 m/s2        ταχύτητα  v = a t = 2,5 t   

  επαγωγική τάση  Εεπαγ = B l v  =  0,01   1  2,5 t  =  0,025 t      

  επαγωγικό ρεύμα   i = Blv / (R+RV) =  0,025 t / 100000 = 2,5 . 10-7 t

ένδειξη βολτομέτρου :   V = i RV  =  2,5 . 10-7 t   (Α)   100000 Ω  =  0,025 t   

    V =  Εεπαγ -  i R  = 0,025 t  -  2  2,5 . 10-7 t  =  0,025 t  -  5 . 10-7 t  = 0,025 t   

 

ΘΕΜΑ  Δ

Δ1.  εξίσωση έντασης του ηλεκτρικού πεδίου  Ε(x,t) = E0 ημ 2π(ft - x/λ) = 300· ημ 2π(1018 t - x/λ )  (S.I.) 

 f  = 1018 Hz     c = λ f  =>  λ = c / f  = 3·108m/s / 1018 Hz =>  λ = 3·10-10m = 0,3 nm < 400 nm (ιώδες)  aκτίνες Χ  ή  υπεριώδες

        B0  =  Ε0 / c  =>   Β0  =  300 V/m  /  3·108 m/s  =  10-6 Τ   

 εξίσωση της έντασης του μαγνητικού πεδίου   Β(x,t) = B0 ημ 2π( ft - x/λ ) = 10-6· ημ 2π(1018 t - 1010 x/3 )   (S.I.) 

 

Δ2.  t=2·10-18s     Ε(x) =  300·ημ 2π(1018·2·10-18 - 1010 x/3 ) =  300·ημ (4π - 2π·1010·x/3) =>

                           Ε(x) = - 300·ημ (2π·1010·x/3)  

 

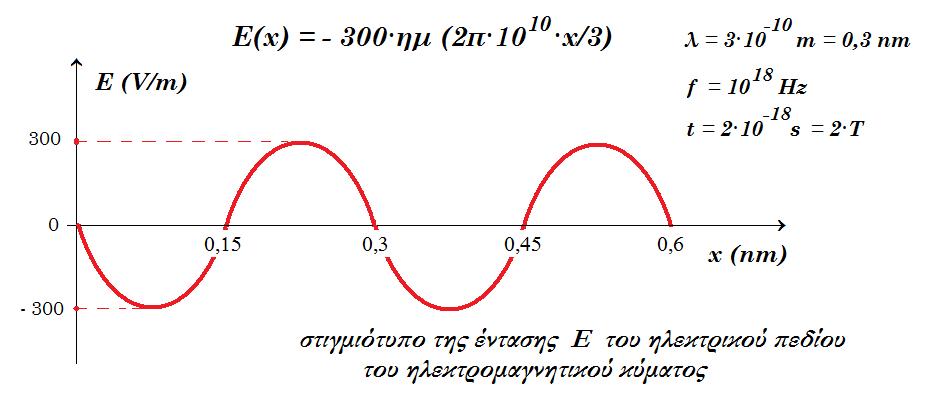
Δ3.  προσπίπτον Η/Μ κύμα :  Β(x,t) = B0  ημ 2π( ft - x/λ ) = 10-6·ημ 2π(1018 t - 1010 x/3 )  (S.I.) 

      ανακλώμενο Η/Μ κύμα : Β'(x,t) = B0 ημ (2πft + 2πx/λ + π) = 10-6·ημ (2π 1018 t + 2π 1010 x/3 + π)  (S.I.) 

      στάσιμο Η/Μ κύμα :  Β"(x,t) = 2 B0 συν (2πx/λ + π/2) ημ (2πft + π/2) = - 2B0 ημ(2πx/λ) συν(2πft) 

                                                = - 2 .10-6· ημ(2π .1010 x/3) συν(2π .1018 t)   (S.I.)      

                                    λ/4 + 3λ/2 = 7λ/4 = 21/4·10-10m

                       κ      δ      κ      δ      κ      δ      κ      δ      κ      δ  Ο μεταλλική επιφάνεια         

 

απόδειξη :                

Β(x,t)  + Β'(x,t)  =  B0  ημ (2πft  -  2πx/λ)  +   B0 ημ (2πft + 2πx/λ + π)  = 

  =  2B0  ημ ( 2πft - 2πx/λ +  2πft + 2πx/λ + π ) / 2    συν ( 2πft - 2πx/λ -  2πft - 2πx/λ - π ) / 2  =

  =  2B0  ημ ( 4πft + π ) / 2   συν ( - 4πx/λ - π ) / 2  =  2B0  ημ ( 2πft + π/2 )  συν ( - 2πx/λ - π/2 )  =   

  =  2B0  συν ( 2πx/λ + π/2 )  ημ ( 2πft + π/2 )  =

  = 2B0  [ συν(2πx/λ) συν(π/2) - ημ(2πx/λ) ημ(π/2) ]  [ ημ(2πft) συν(π/2)+ συν(2πft)  ημ(π/2) ] =  

  = 2B0 [ - ημ (2πx/λ) ] [ + συν (2πft) ] = - 2B0 ημ(2πx/λ)  συν(2πft)      

ημα + ημβ = 2 ημ(α + β)/2  συν(α - β)/2

 

Δ4.      E = h f   =  6,6 10-34 J.s  1020 Hz  =  6,6 10-14 J     ενέργεια προσπίπτοντος φωτονίου     

     λ = c / f  = 3·108m/s / 1020 Hz =>  λ = 3·10-12m  =  3 pm 

    φαινόμενο Compton :   λ' - λ  =  h / mc ( 1 - συν90° ) =>

=> λ' - 3 10-12 m = 6,6 10-34 / ( 9 10-31  3 108 ) ( 1 - 0 ) = 0,24 10-11 m  => λ' - 3 10-12 m = 2,4 10-12 m  =>

=>  λ'  =  5,4 10-12 m  = 5,4 pm        

    f ' = c / λ'  =  3 108 / 5,4 10-12  =  0,55 1020 Hz    συχνότητα σκεδαζομένου φωτονίου 

  ενέργεια σκεδαζομένου φωτονίου :  E' = h f '  = 6,6 10-34 J.s   0,55 1020 Hz = 3,63 10-14 J  = 2,27 .103  eV  

διατήρηση ορμής :  pe,x = E/c =>  pe  συνθ = h / λ   (1)         pe,y = E'/c =>  pe  ημθ = h / λ'   (2)  

          (2) / (1) =>  εφθ  =  λ / λ' =  3 pm / 5,4 pm  =>  εφθ  = 0,55     

 

Δ5.       h f  +  eV  =  Ke  + φ  =>   6,6 10-34  6 1014   +  1,6 10-19  1  =  Ke  +  2,4 . 1,6 10-19  =>

               =>  39,6 10-20  + 1,6 10-19 =  Ke  +  3,84 10-19  =>  0,12 10-19  +  1,6 10-19  =  Ke  = 1,72 .10-19 J   

 h f  +  eV  =  Ke  + φ  =>  h f  +  e V0  =   φ  =>   6,6 10-34  6 1014   +  1,6 10-19  V0   = 2,4 1,6 10-19  => 

              =>  3,96 10-19 + 1,6 10-19  V0  =  3,84 10-19  =>  - 0,12 10-19  /  1,6 10-19  = V0 = - 0,12 / 1,6 V = - 0,075 V

f  = c / λ =  3 108 / 5 10-7 =  0,6 1015 Hz  =  6 1014 Hz                   V  =   φ/e  -  h/e  f           f0 = φ/e   

 h f  +  eV  =  Ke  + φ  =>   6,6 10-34  6 1014   +   eV   =   Ke  +   6,25 . 1,6 10-19  =>

               =>  39,6 10-20   + eV   =  Ke  +  10 10-19  =>   40 10-20   + eV   =  Ke  +  10 10-19  =>   4 10-19   +  eV   =  Ke  +  10 10-19  =>   - 6 10-19   +  eV   =  Ke    όση τάση και να βάλουμε τα ηλεκτρόνια δεν βγαίνουν από την επιφάνεια του λευκοχρύσου διότι η ακτινοβολία έχει μικρή συχνότητα    για να βγουν ηλεκτρόνια από την επιφάνεια του λευκοχρύσου  πρέπει η συχνότητα να είναι :   h f0  =  φ  =>  f0  =  φ / h = 6,25 1,6 10-19 / 6,6 10-34  =>  f0 =  1,5 1015 Hz     λ0 = c / f0 =  3 108 / 1,5 1015 = 2 10-7  m  = 200 10-9 m  = 200 nm  <  400 nm  (ιώδες)          πρέπει η ακτινοβολία να είναι υπεριώδης