ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΣΧΟΛΙΚΟ ΕΤΟΣ 2024-2025
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΗΜΕΡΟΜΗΝΙΑ : 20 / 5 / 2025
ΠΕΡΙΦΕΡΕΙΑΚΗ ΔΙΕΥΘΥΝΣΗ Π/ΘΜΙΑΣ & ΤΑΞΗ : Γ' ΛΥΚΕΙΟΥ
Δ/ΘΜΙΑΣ ΕΚΠΑΙΔΕΥΣΗΣ ΑΤΤΙΚΗΣ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ προσανατολισμού
ΔΙΕΥΘΥΝΣΗ Δ/ΘΜΙΑΣ ΕΚΠ/ΣΗΣ Β' ΑΘΗΝΑΣ Ονοματεπώνυμο :
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΨΥΧΙΚΟΥ ΕΙΣΗΓΗΤΗΣ : Ανδρούτσος Θεόδωρος
ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2025
ΘΕΜΑΤΑ
ΘΕΜΑ Α
Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση.
Α.1. Το κύκλωμα του σχήματος περιλαμβάνει δυο λείους οριζόντιους αγωγούς x′x και y′y, χωρίς ωμική αντίσταση απέχουν απόσταση ℓ. Στο αριστερό τους άκρο συνδέονται στα σημεία Α και Γ με ιδανικό πηνίο συντελεστή αυτεπαγωγής L. Τρίτος αρχικά ακίνητος αγωγός ΚΝ μάζας m, χωρίς ωμική αντίσταση και μήκους ℓ μπορεί να κινείται μένοντας διαρκώς οριζόντιος με τα άκρα του σε συνεχή επαφή με τους αγωγούς x′x και y′y. Το επίπεδο του κυκλώματος είναι εντός ενός κατακόρυφου ομογενούς μαγνητικού πεδίου έντασης μέτρου Β και του ομόρροπου γήινου ομογενούς βαρυτικού πεδίου έντασης μέτρου g. Τη χρονική στιγμή t0 = 0, δίνουμε στον αγωγό ΚΝ οριζόντια ταχύτητα υ0 παράλληλη στους αγωγούς x′x και y′y.

α. Το ρεύμα που διαρρέει τον αγωγό ΚΝ είναι εναλλασσόμενο με μέγιστη ένταση : I0 = √(m/L) ∙ v0
β. Ο αγωγός ΚΝ θα εκτελέσει αρμονική ταλάντωση διότι η συνισταμένη δύναμη ΣF που δέχεται είναι ανάλογη με την απομάκρυνση x σύμφωνα με την σχέση : ΣF = - Bl/L ∙ x
γ. Τίποτα από τα ανωτέρω.
Επιλέξτε την σωστή απάντηση. μονάδες 5
Α.2. Ας θεωρήσουμε το πρότυπο του Bohr για το άτομο του υδρογόνου. Στη θεμελιώδη κατάσταση, το άτομο έχει ενέργεια 𝚬𝟏, ενώ το ηλεκτρόνιό του περιφέρεται σε κυκλική τροχιά, ακτίνας 𝐫𝟏, με κέντρο τον πυρήνα του. Στο κέντρο αυτής της κυκλικής τροχιάς, σύμφωνα με τον Bohr, το γινόμενο |𝚿𝟐|𝐝𝐕, όπου 𝚿 η κυματοσυνάρτηση του ηλεκτρονίου και 𝐝𝐕 ένας στοιχειώδης όγκος γύρω από το σημείο αυτό, θα είχε τιμή:
α) |𝚿𝟐|𝐝𝐕 = 𝟎, β) |𝚿𝟐|𝐝𝐕 = 𝟏, γ) 𝟎 < |𝚿𝟐|𝐝𝐕 < 𝟏, δ) τίποτα από αυτά.
Επιλέξτε την σωστή απάντηση. μονάδες 5
Α.3. Στο κύκλωμα του σχήματος μια ηλεκτρική πηγή συνεχούς ρεύματος συνδέεται με μεταβλητή αντίσταση (ροοστάτης) και δύο κλάδους παράλληλους. Ο ένας κλάδος περιλαμβάνει λαμπτήρα με ωμική αντίσταση RΛ και ο άλλος πηνίο με ωμική αντίσταση Rπ ( RΛ > Rπ ). Ο διακόπτης δ είναι κλειστός. Τοποθετούμε τον δρομέα σε ορισμένη θέση έτσι ώστε ο λαμπτήρας να φωτοβολεί ελάχιστα και ανοίγουμε τον διακόπτη. 

α) Ο λαμπτήρας σβήνει αμέσως.
β) Ο λαμπτήρας φωτοβολεί αμυδρά για κάποιο χρονικό διάστημα και μετά σβήνει.
γ) Ο λαπτήρας αρχικά φωτοβολεί πιο έντονα και σβήνει μετά από κάποιο χρονικό διάστημα.
δ) Τίποτα από τα παραπάνω.
Επιλέξτε την σωστή απάντηση. μονάδες 5
Α.4. Σωμάτιο α (πυρήνας ηλίου) κινούμενο προς ένα ακίνητο πυρήνα χρυσού διαγράφει την τροχιά του σχήματος.
 Η περίπτωση αυτή
Η περίπτωση αυτή
α) δεν θεωρείται κρούση. β) μπορεί να θεωρηθεί έκκεντρη κρούση.
γ) μπορεί να θεωρηθεί κεντρική κρούση. δ) μπορεί να θεωρηθεί πλαστική κρούση.
Επιλέξτε την σωστή απάντηση. μονάδες 5
Α.5. μονάδες 5
Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα την λέξη Σωστό, για την σωστή πρόταση, και την λέξη Λάθος, για την λανθασμένη.
α. Μεταλλική σφαίρα αμελητέας ακτίνας φέρει ηλεκτρικό φορτίο -17∙10-19 C.
β. Στο φάσμα της ηλεκτρομαγνητικής ακτινοβολίας το πορτοκαλί φως έχει μικρότερο μήκος κύματος από τις ακτίνες Χ και μεγαλύτερη συχνότητα από το υπεριώδες.
γ. Σε χαμηλές θερμοκρασίες (310°K) το μέλαν σώμα εκπέμπει στο υπέρυθρο.
δ. Hλεκτρόνιο περιστρέφεται γύρω από συνεχώς ακίνητο πρωτόνιο με σταθερή συχνότητα περιστροφής f σε ακτίνα r. Το διάνυσμα της στροφορμής L του ηλεκτρονίου και το διάνυσμα της έντασης Β του μαγνητικού πεδίου που δημιουργεί, είναι ομόρροπα.
ε. Στα άκρα αντίστασης 5 Ω εφαρμόζεται εναλλασσόμενη τάση. Η ισχύς που καταναλώνεται στην αντίσταση δίνεται από τη σχέση : P(t) = 10 - 10 συν(10π∙t). H εξίσωση του ρεύματος που διαρρέει την αντίσταση συναρτήσει του χρόνου είναι : i(t) = 2∙ημ(10πt).
ΘΕΜΑ Γ
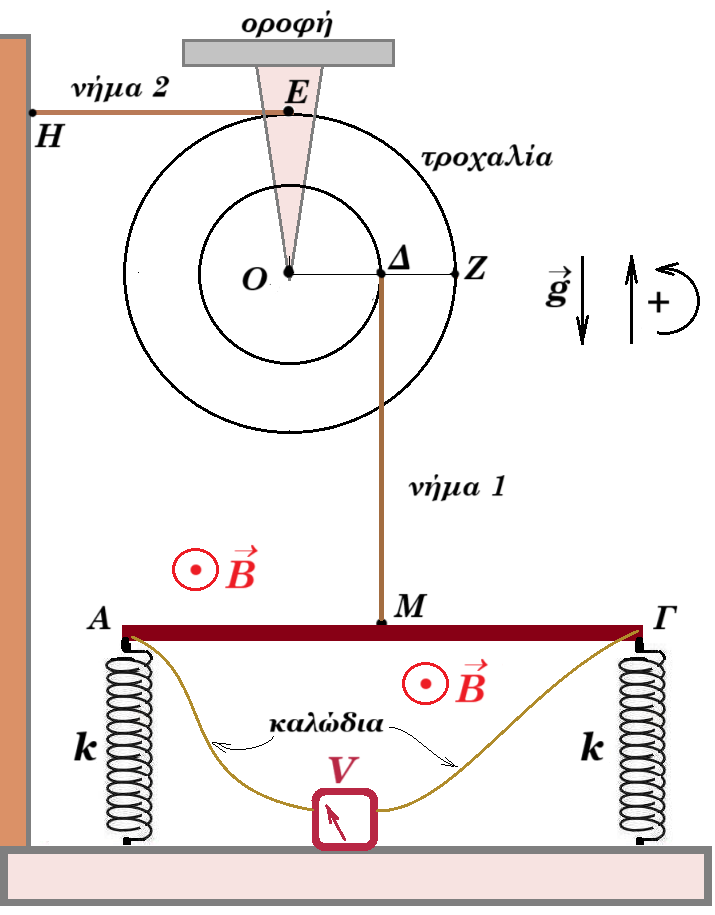 |
Γ1. Η διάταξη του σχήματος ισορροπεί, η αγώγιμη ράβδος ΑΓ είναι ακίνητη, έχει μάζα m = 0,5 kg μήκος l = 0,5 m ωμική αντίσταση RΑΓ = 1 Ω. Τα ιδανικά ελατήρια είναι όμοια, έχουν σταθερά k = 1250 N/m. Τα νήματα είναι αβαρή μη εκτατά, το νήμα 1 είναι τυλιγμένο γύρω από τον μικρό δακτύλιο ακτίνας (0Δ) = 0,2 m της αβαρούς τροχαλίας, ενώ το νήμα 2 είναι τυλιγμένο γύρω από τον μεγάλο δακτύλιο ακτίνας (0Ζ) = 0,5 m. Στο σημείο Η η τάση του νήματος είναι ΤΗ = 10 Ν. Η ένταση του ομογενούς μαγνητικού πεδίου είναι Β = 0,1 Τ. Τη στιγμή t0 = 0 με απαλή φλόγα κεριού κόβουμε το νήμα 1. Μελετήστε την κίνηση της ράβδου ΑΓ και βρείτε την ένδειξη του ιδανικού βολτομέτρου. μονάδες 7
|
Γ2. Λεπτή δέσμη ηλεκτρομαγνητικής ακτινοβολίας συχνότητας f=6∙1014Hz που διαδίδεται στον αέρα προσπίπτει κάθετα σε επίπεδη μεταλλική επιφάνεια έστω στο σημείο Ο και ανακλάται χωρίς απώλεια ενέργειας. Η μέγιστη ένταση του ηλεκτρικού πεδίου είναι 300 V/m.
α) Σχεδιάστε την ένταση B(x) του μαγνητικού πεδίου του προσπίπτοντος κύματος στο χρονικό διάστημα [0 , 10-14s] ενώ μετρώντας από την επιφάνεια (σημείο Ο) πόσα σημεία είναι σκοτεινά και πόσα έχουν μέγιστη φωτεινότητα σε μήκος 0,506 mm; μονάδες 4
β) Εξηγήστε γιατί τα κάρβουνα φαίνονται μαύρα στους 27°C ενώ αν ανέβει η θερμοκρασία φαίνονται κόκκινα και στον λαμπτήρα πυρακτώσεως το σύρμα βολφραμίου εκπέμπει λευκό φως (ή ελαφρώς κίτρινο) όταν ο λαμπτήρας φωτοβολεί. μονάδες 3
Γ3. Φωτόνιο της ηλεκτρομαγνητικής ακτινοβολίας συχνότητας f = 1020 Hz σκεδάζεται από ακίνητο ηλεκτρόνιο. Το σκεδαζόμενο φωτόνιο κινείται κάθετα ως προς τη διεύθυνση του προσπίπτοντος φωτονίου.
α) Βρείτε την εφαπτομένη της γωνίας που σχηματίζει η ταχύτητα του ηλεκτρονίου αμέσως μετά την σκέδαση, με τη διεύθυνση της κίνησης του αρχικού φωτονίου. h = 20/3∙10-34J∙s h/mc = 2,4pm μονάδες 3
β) Το ηλεκτρόνιο εισέρχεται στο εσωτερικό του σωληνοειδούς με μήκος L=12,5 m, 2180 σπείρες, από τη μία άκρη, έτσι ώστε η ταχύτητά του σχηματίζει με τον άξονα του σωληνοειδούς γωνία φ=60° και εξέρχεται από την άλλη άκρη, Υπολογίστε το μήκος της τροχιάς που διαγράφει το ηλεκτρόνιο μέσα στο σωληνοειδές. μονάδες 3
γ) Στο σχήμα φαίνεται η διάταξη για την εξαγωγή ηλεκτρονίων από μια μεταλλική επιφάνεια όταν προσπέσει σ'αυτή Η/Μ ακτινοβολία. Δίνονται: E = 12 V r = 1 Ω RΚΛ = 10 Ω (ΚΛ) = 0,5 m
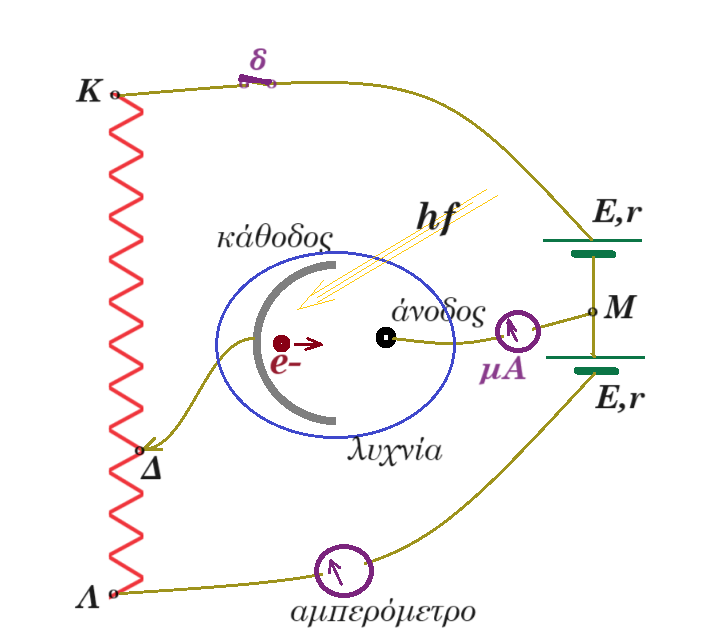 |
Μετακινώντας τον δρομέα Δ από το άκρο Κ έως το άκρο Λ της αντίστασης λαμβάνουμε τάση VMΔ θετική, αρνητική ή μηδενική. Έστω ότι ο δρομέας είναι στη θέση όπου (ΚΔ) = 0,3m. Εάν στην κάθοδο προσπέσει ακτινοβολία συχνότητας f=6∙1014Hz υπολογίστε την κινητική ενέργεια ενός ηλεκτρονίου που εξέρχεται από την επιφάνεια του μετάλλου, όταν φθάνει στην άνοδο. Έργο εξαγωγής μετάλλου φ = 2eV. μονάδες 5
|
ΘΕΜΑ Δ
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Απαντήστε σε όλα τα θέματα, 25 μονάδες το κάθε ένα. ΚΑΛΗ ΕΠΙΤΥΧΙΑ
Ο ΔΙΕΥΘΥΝΤΗΣ Ο ΕΙΣΗΓΗΤΗΣ
Καΐρης Αλέξανδρος Ανδρούτσος Θεόδωρος
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Γ1) 10 Ν 0,5 m = TΜ 0,2 m => ΤΜ = 25 Ν προς τα πάνω
ΤΜ = mg + Fελ => 25 = 5 + Fελ => Fελ = 20 N = 2k Δl => Δl = 20 / 2500 = 0,008 m = 8 mm επιμήκυνση
2k = m ω2 => 2500 = 0,5 ω2 => ω2 = 2 2500 => ω = 50∙√2 rad/s
mg = 2k x0 => 5 = 2500 x0 => x0 = 0,002 m = 2 mm συσπείρωση Α = 8 mm + 2 mm = 10 mm = 0,01 m
η ράβδος εκτελεί Α.Α.Τ. με πλάτος Α = 0,01 m και κυκλική συχνότητα ω = 50∙√2 rad/s
x(t) = 0,01 ∙ ημ(50∙√2∙t + π/2) υ(t) = 0,5∙√2 ∙ ημ(50√2∙t + π/2)
στα άκρα της ράβδου επάγεται τάση : Εεπ(t) = Β l υ(t) = 0,1 ∙ 0,5 ∙ 0,5√2 ημ(50∙√2∙t + π/2) = 0,025√2 ημ(50∙√2∙t + π/2)
ένδειξη βολτομέτρου : V = 0,025 Volt = 25 mV ενεργός τάση
Γ2. εξίσωση έντασης του ηλεκτρικού πεδίου Ε(x,t) = E0 ημ 2π(ft - x/λ) = 300· ημ 2π(6·1014 t - x/λ ) (S.I.)
f = 6·1014 Hz Τ = 1/6·10-14 s c = λ f => λ = c / f = 3·108m/s / 6·1014 Hz => λ = 0,5·10-6m = 500 nm πράσινο
B0 = Ε0 / c => Β0 = 300 V/m / 3·108 m/s = 10-6 Τ 10-14s = 6 T έξι περίοδοι
εξίσωση έντασης μαγνητικού πεδίου Β(x,t) = B0 ημ 2π( f∙t - x/λ ) = 10-6· ημ 2π(6·1014 t - 2·106 x ) (S.I.)
Εάν προσπέσει ακτινοβολία με συχνότητα : f = 6 ∙1014 Hz δηλαδή μήκος κύματος : λ = c / f = 3∙108 m/s / 6∙1014 Hz = 0,5∙10-6 m = 5∙10-7 m = 500 nm πράσινο N = 0,506 ∙10-3 m / 0,5∙10-6 m = 1012 μήκη κύματος = 2024 κοιλίες (μέγιστη φωτεινότητα) 2025 δεσμοί (σκοτεινά σημεία)
Γ3.
α) λ = c / f = 3·108m/s / 1020 Hz => λ = 3·10-12m = 3 pm
φαινόμενο Compton : λ' - λ = h / mc (1 - συν90°) => λ' - 3 10-12 m = 2,4 10-12 m
=> λ' - 3 10-12 m = 2,4 10-12 m => λ' = 5,4 10-12 m = 5,4 pm
διατήρηση ορμής : pe,x = E/c => pe συνθ = h / λ (1) pe,y = E'/c => pe ημθ = h / λ' (2)
(2) / (1) => εφθ = λ / λ' = 3 pm / 5,4 pm => εφθ = 5/9
β) vy = v ημ60° vx = v συν60° = v/2 t = L/(v/2) = 2L/v
s = v t = 2L = L/συν60° = 2 12,5 m = 25 m
γ)
Ισχύει η διατήρηση της ενέργειας : h.f + e.VMΔ = Ke + φ
όπου φ είναι το έργο εξαγωγής του μετάλλου δηλαδή η ενέργεια που πρέπει να προσλάβει το ηλεκτρόνιο του ατόμου της μεταλλικής επιφάνειας για να εξέλθει του ατόμου, το άτομο γίνεται ιόν
Έστω ότι ο δρομέας είναι στη θέση όπου (ΚΔ) = 0,3 m τότε RΚΔ / RΚΛ = (ΚΔ) / (ΚΛ) => RΚΔ / 10 Ω = 0,3 m / 0,5 m => RΚΔ = 6 Ω και RΔΛ = 4 Ω
εφαρμόζουμε τον νόμο του Ohm στον μεγάλο βρόχο οπότε έχουμε : 2.Ε = i ( 2.r + RΚΛ ) =>
=> 2 . 12 V = i ( 2 . 1 Ω + 10 Ω ) => i = 24 / 12 Ω => i = 2 A η ένδειξη του αμπερομέτρου είναι 2 Α
στον βρόχο ΜΔΛΜ έχουμε : Ε = VMΔ + i ( r + RΔΛ ) => 12 V = VMΔ + 2 A ( 1 Ω + 4 Ω ) => 12 V - 10 V = VMΔ => VMΔ = 2 V η άνοδος έχει υψηλότερο δυναμικό από την κάθοδο
στον βρόχο ΜΚΔΜ έχουμε : Ε = i ( r + RΚΔ ) + VΔM => 12 V = 2 A ( 1 Ω + 6 Ω ) + VΔM => 12 V - 14 V = VΔM => VΔM = - 2 V => VMΔ = 2 V η άνοδος έχει υψηλότερο δυναμικό από την κάθοδο
Εάν προσπέσει ακτινοβολία με συχνότητα : f = 6 ∙1014 Hz δηλαδή μήκος κύματος : λ = c / f = 3.108 m/s / 6.1014 Hz = 0,5.10-6 m = 5.10-7 m = 500 nm πράσινο κάθε φωτόνιο έχει ενέργεια : Ε = h.f = 20/3 .10-34 J.s 6.1014 Hz = 40 ∙10-20 J = 4.10-19 J / 1,6.10-19 C/e = 2,5 eV > 2 eV = φ οπότε h.f + e.VMΔ = Ke + φ => 2,5 eV + e. 2V = Ke + 2 eV => Ke = 2,5 eV = 2,5 1,6.10-19 J = 4 .10-19 J κινητική ενέργεια των εξερχομένων από το μέταλλο ηλεκτρονίων όταν φθάνουν στην άνοδο
4.10-19 J = 0,5 9.10-31 kg u2 => u = 0,94.106 m/s ταχύτητα των ηλεκτρονίων όταν φθάνουν στην άνοδο
h.f + e.V = K + φ => 2,5 eV + e.V0 = 0 + 2 eV => V0 = - 0,5 V τάση αποκοπής
ένα φωτόνιο ενέργειας Ε = hf = 4.10-19 J / 1,6.10-19 C/e = 2,5 eV προσπίπτει σε ένα ηλεκτρόνιο ενός ατόμου της μεταλλικής επιφάνειας και του "δίνει" όλη την ενέργειά του 2,5 eV επειδή το έργο εξαγωγής του μετάλλου δηλαδή το ποσό της ενέργειας για να εξέλθει το ηλεκτρόνιο από το άτομο είναι φ = 2 eV η διαφορά 0,5 eV είναι η κινητική ενέργεια του ηλεκτρονίου μόλις βγει από το άτομο αλλά επειδή υπάρχει διαφορά δυναμικού VMΔ = 2V μεταξύ ανόδου και καθόδου το ηλεκτρόνιο οδεύει προς την άνοδο κερδίζοντας ενέργεια από το ηλεκτρικό πεδίο e.VMΔ = e. 2V = 2 eV οπότε το ηλεκτρόνιο φθάνει στην άνοδο έχοντας ενέργεια 0,5 eV + 2 e V = 2,5 e V = Ke
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Α.1. (a) Α.2. (α) στον πυρήνα του ατόμου δεν βρίσκεται το e- σύμφωνα με το πρότυπο Borh
Α5. (α) Λ Ν = 17∙10-19 C / 1,6∙10-19 C = 10,625 ηλεκτρόνια ΟΧΙ ΑΚΕΡΑΙΟΣ ΑΡΙΘΜΟΣ ,
(β) Λ, (γ) Σ , (δ) Λ (ε) Λ i(t) = 2∙ημ(5πt)
πλήρης επίλυση του Α1
Εεπαγ + ΕΑΥΤ = i R = 0 => B v l - L di/dt = 0 => B l dx/dt = L di/dt =>
=> B l Δx/Δt = L Δi/Δt => B l (x - 0) = L (i - 0) => Β l x = L i =>
=> i = Bl/L x = 0,2T 0,5m / 0,0025H x => i = 40.x
ΣF = - FL = - B l i = - 0,2 0,5 40.x => ΣF = - 4.x
ΣF = - B2l2/L x = m a => a = - B2l2/mL x = - ω2 x => ω2 = B2l2/mL v0 = ω Α
I = √(m/L) v0 = √(m/L) ω Α = √(m/L) Bl/√(mL) Α = Bl/L Α
ΣF = m a => m a = - B l i => 0,04 a = - 0,2 0,5 40.x => a = - 100 x
ω2 = 100 => ω = 10 rad/s T = 2π/10 = π/5 s
η αρχική κινητική ενέργεια του αγωγού μετατρέπεται σε δυναμική ενέργεια στο μαγνητικό πεδίο του πηνίου
έστω η αρχική ταχύτητα v0 = 2 m/s m = 0,04 kg L = 0,0025 H
Kmax = UL,max => 0,5 m v02 = 0,5 L I2 => I = √(m/L) ∙ v0 = √(0,04/0,0025) 2 = 4 2 => Ι = 8 A μέγιστη ένταση ρεύματος που διαρρέει την ράβδο και το πηνίο
Ι = 40 xmax => 8 = 40 xmax => xmax = 0,2 m μέγιστη απομάκρυνση της ράβδου από τη θέση ισορροπίας της ( πλάτος ταλάντωσης της ράβδου )
η ράβδος εκτελεί Α.Α.Τ. με πλάτος 0,2 m και περίοδο π/5 s
οπότε x = 0,2 ημ(10π.t) αρχικά βρίσκεται στη θέση ισορροπίας της
τότε το ρεύμα i = 40.x = 40 0,2 ημ(10π.t) => i(t) = 8 ημ(10π.t)
Kmax = UL,max = K + UL => K + UL = 0,5 m v02 = 0,5 0,04 22 => K + UL = 0,08 J => K = 0,08J - UL
x = 0,2 ημ(10π.t) v = 2 συν(10π.t) a = - 20 ημ(10π.t)
|αmax| = 20 m/s2 |a| = 10 m/s2 = 20 ημ(10π.t) => ημ(10π.t) = 0,5
x = 0,2 ημ(10π.t) = 0,2 0,5 = 0,1 m

![]()

 Η περίπτωση αυτή
Η περίπτωση αυτή
