ΘΕΜΑ Γ Η ομογενής δοκός ΑΓ του διπλανού σχήματος μάζας Μ και μήκους l=2m έχει το άκρο της Α στερεωμένο σε άρθρωση σε κατακόρυφο τοίχο. Στο άλλο άκρο Γ είναι δεμένο αβαρές μη ελαστικό νήμα ν1 το οποίο σχηματίζει με τη δοκό γωνία φ ενώ το άλλο άκρο του στερεώνεται στο σημείο Δ κατακόρυφου τοίχου, όπως φαίνεται στο σχήμα. Αν το νήμα ν1 ήταν ελαστικό και στερεώνονταν ακλόνητα τα άκρα του, από τη συμβολή δύο τρεχόντων κυμάτων μήκους κύματος λ=l  θα δημιουργούνταν κατά μήκος του στάσιμο κύμα στο οποίο θα υπήρχαν συνολικά 5 ακίνητα σημεία. Στο άκρο Γ δένεται ένα δεύτερο κατακόρυφο αβαρές μη ελαστικό νήμα ν2, στο άλλο άκρο του οποίου κρέμεται σώμα Σ1 μάζας m1=1Kg. Στην κατάσταση ισορροπίας του συστήματος δοκός – σώμα Σ1 το μέτρο της τάσης του νήματος ν1 είναι Tν1=Μg√3 Ν.

Γ1. Να αποδείξετε ότι η μάζα Μ της δοκού είναι ίση με τη μάζα m1 του σώματος Σ1. (Μονάδες 7)
Γ2. Αν το όριο θραύσης του νήματος ν1 είναι Tθρ=20 √3 Ν, να βρείτε τη μεγαλύτερη απόσταση από το άκρο Α που  μπορεί να τοποθετηθεί πάνω στη δοκό ένα σώμα Σ μάζας m=2Kg χωρίς το νήμα ν1 να κοπεί. (Μονάδες 5)
Κάτω από το αρχικό σύστημα δοκός – σώμα Σ1, στερεώνουμε το σώμα Σ2  μάζας m2=1Kg στο πάνω άκρο ενός κατακόρυφου ιδανικού ελατηρίου σταθεράς k=100N/m, το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο στο οριζόντιο δάπεδο.
Ο άξονας του ελατηρίου βρίσκεται στη διεύθυνση του νήματος ν2.
Μετακινούμε το σώμα Σ2 προς τα πάνω μέχρι να φθάσει στη θέση φυσικού μήκους του ελατηρίου και το εκτοξεύουμε προς τα κάτω με ταχύτητα μέτρου υ0=√3 m/s.  Το σύστημα ελατήριο – σώμα Σ2 εκτελεί απλή αρμονική ταλάντωση με σταθερά ταλάντωσης D=k.
Γ3. Να υπολογίσετε το μέτρο της μέγιστης ταχύτητας ταλάντωσης του συστήματος ελατήριο – σώμα Σ2. (Μονάδες 5)
Γ4. Κάποια χρονική στιγμή καθώς το σύστημα ελατήριο – Σ2 εκτελεί απλή αρμονική ταλάντωση, κόβουμε το νήμα ν2 οπότε το σώμα Σ1 πέφτει από ύψος h=0,2m και συγκρούεται με το σώμα Σ2 κεντρικά και πλαστικά.  Οι ταχύτητες των σωμάτων είναι αντίθετες την στιγμή της κρούσης.
Tο συσσωμάτωμα που δημιουργείται εκτελεί απλή αρμονική ταλάντωση με σταθερά ταλάντωσης D=k. Να προσδιορίσετε τη θέση της κρούσης των σωμάτων. Αν θεωρήσουμε ως χρονική στιγμή t=0 τη χρονική στιγμή που το συσσωμάτωμα αρχίζει να ταλαντώνεται και θετική φορά για την απομάκρυνση προς τα πάνω, να γράψετε την εξίσωση της απομάκρυνσης για την απλή αρμονική ταλάντωση του συσσωματώματος y=f(t).
Δίνεται η επιτάχυνση της βαρύτητας g=10m/s². (Μονάδες 8)

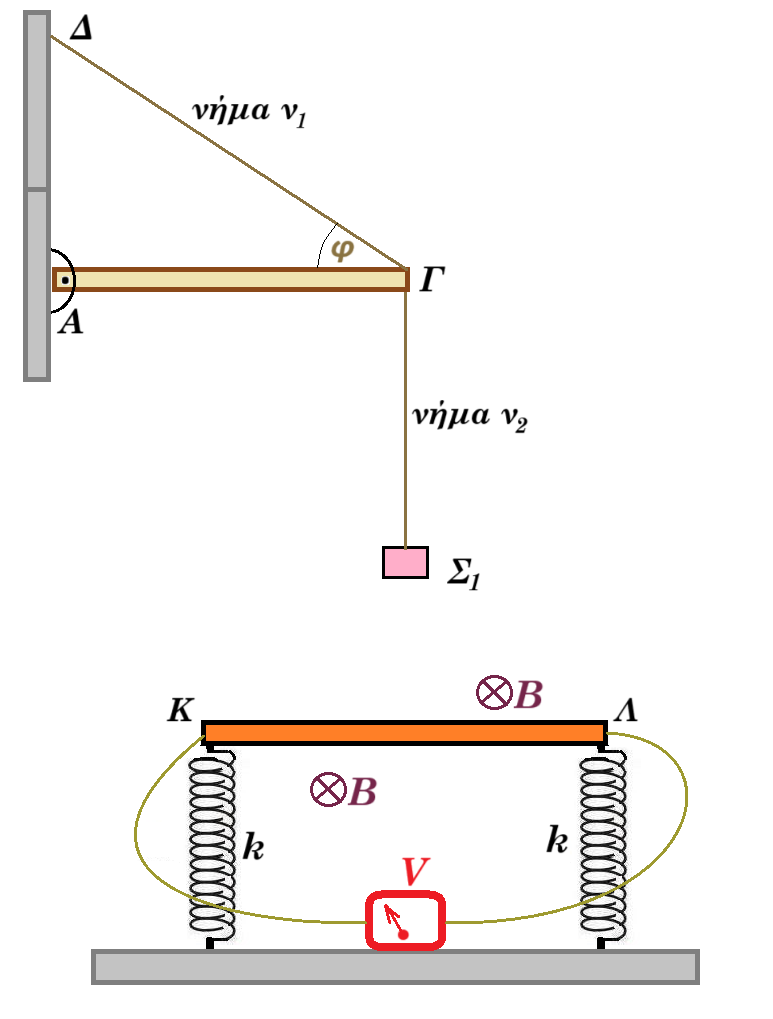
ΘΕΜΑ Γ Η ομογενής δοκός ΑΓ του διπλανού σχήματος μάζας Μ και μήκους l=2m έχει το άκρο της Α στερεωμένο σε άρθρωση σε κατακόρυφο τοίχο. Στο άλλο άκρο Γ είναι δεμένο αβαρές μη ελαστικό νήμα ν1 το οποίο σχηματίζει με τη δοκό γωνία φ ενώ το άλλο άκρο του στερεώνεται στο σημείο Δ κατακόρυφου τοίχου, όπως φαίνεται στο σχήμα. Αν το νήμα ν1 ήταν ελαστικό και στερεώνονταν ακλόνητα τα άκρα του, από τη συμβολή δύο τρεχόντων κυμάτων μήκους κύματος λ=l  θα δημιουργούνταν κατά μήκος του στάσιμο κύμα στο οποίο θα υπήρχαν συνολικά 5 ακίνητα σημεία. Στο άκρο Γ δένεται ένα δεύτερο κατακόρυφο αβαρές μη ελαστικό νήμα ν2, στο άλλο άκρο του οποίου κρέμεται σώμα Σ1 μάζας m1=1Kg πολύ μικρών διαστάσεων από πλαστελίνη. Στην κατάσταση ισορροπίας του συστήματος δοκός – σώμα Σ1 το μέτρο της τάσης του νήματος ν1 είναι Tν1=Μg√3 Ν.

Γ1. Να αποδείξετε ότι η μάζα Μ της δοκού είναι ίση με τη μάζα m1 του σώματος Σ1. (Μονάδες 5)
Γ2. Αν το όριο θραύσης του νήματος ν1 είναι Tθρ=20 √3 Ν, να βρείτε τη μεγαλύτερη απόσταση από το άκρο Α που  μπορεί να τοποθετηθεί πάνω στη δοκό ένα σώμα Σ μάζας m=2Kg χωρίς το νήμα ν1 να κοπεί. (Μονάδες 5)
Κάτω από το αρχικό σύστημα δοκός – σώμα Σ1, στερεώνουμε την ράβδο ΚΛ,  μάζας m2=1Kg,  ωμικής αντίστασης R=2Ω στο πάνω άκρο δύο όμοιων κατακόρυφων ιδανικών ελατηρίων σταθεράς k=500N/m, το άλλο άκρο των οποίων είναι ακλόνητα στερεωμένα στο οριζόντιο μονωτικό δάπεδο.  Η διεύθυνση του νήματος ν₂  διέρχεται από το μέσον της ράβδου ΚΛ.  Στον χώρο υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο εντάσεως Β=0,01Τ.  Τα άκρα της ράβδου συνδέονται με ιδανικό βολτόμετρο.
Τη χρονική στιγμή t₀=0 μετακινούμε την ράβδο προς τα πάνω μέχρι να φθάσει στη θέση φυσικού μήκους των ελατηρίων, την εκτοξεύουμε προς τα κάτω με ταχύτητα μέτρου υ0=√3/π m/s  και κόβουμε το νήμα ν2  οπότε το σώμα Σ1 πέφτει από ύψος h=1,25m και συγκρούεται με την ράβδο κεντρικά και πλαστικά.. 
Γ3. Να υπολογίσετε το μέτρο της μέγιστης ταχύτητας ταλάντωσης του συστήματος ελατήρια – ράβδος ΚΛ πριν την κρούση. (Μονάδες 5)
Γ4. Tο συσσωμάτωμα που δημιουργείται εκτελεί απλή αρμονική ταλάντωση. Να προσδιορίσετε τη θέση της κρούσης των σωμάτων.  Θεωρούμε θετική φορά για την απομάκρυνση προς τα πάνω. Μελετήστε την κίνηση του συσσωματώματος.  Βρείτε την ένδειξη του βολτομέτρου.
Δίνεται η επιτάχυνση της βαρύτητας g=10m/s². (Μονάδες 10)

ΘΕΜΑ Δ Το κύκλωμα του σχήματος βρίσκεται σε κατακόρυφο επίπεδο και στηρίζεται σε δύο στηρίγματα από μονωτικό υλικό. Η πηγή εναλλασσόμενης τάσης παρέχει ημιτονοειδή τάση της μορφής v=Vημ100πt (S.I) και η συσκευή Σ έχει ενδείξεις κανονικής λειτουργίας <<16W, 8V>>. Ο αγωγός ΚΛ μήκους =1m, μάζας m=0,05kg και ωμικής αντίστασης R=4Ω που έχει τα άκρα του Κ και Λ σε επαφή με δύο κατακόρυφα σύρματα ΑΗ και ΓΘ μεγάλου μήκους και αμελητέας ωμικής αντίστασης με τα οποία δεν παρουσιάζει τριβές, συγκρατείται ακίνητος σε οριζόντια θέση με τη βοήθεια κατακόρυφης εξωτερικής δύναμης μέτρου F που ασκείται στο μέσο του και βρίσκεται μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης Β=0,5Τ κάθετο στο επίπεδο του σχήματος που έχει φορά από τον αναγνώστη προς τη διάταξη και περιορίζεται στην περιγεγραμμένη περιοχή του σχήματος. Αρχικά οι διακόπτες δ1 και δ2 είναι ανοικτοί και την χρονική στιγμή t0=0 κλείνουν ταυτόχρονα. Το ρεύμα στο χρονικό διάστημα (0 - Τ/2) όπου Τ= η περίοδος της εναλλασσόμενης τάσης έχει φορά από το Α προς το Μ  (Α Μ).

Δ1. Αν η συσκευή Σ λειτουργεί κανονικά, να υπολογίσετε το πλάτος V της εναλλασσόμενης τάσης.(Μονάδες 5)
Δ2. Να υπολογίσετε τη μέση ισχύ που καταναλώνει το κύκλωμα. (Μονάδες 4)
Δ3. Τη χρονική στιγμή t1=0,1325 s να προσδιορίσετε την κατεύθυνση της εξωτερικής δύναμης F (Μονάδες 4)
και να υπολογίσετε το μέτρο της. (Μονάδες 6)
Κάποια χρονική στιγμή ανοίγουμε το διακόπτη δ1 και ταυτόχρονα καταργούμε την εξωτερική δύναμη F και αφήνουμε τον αγωγό ΚΛ ελεύθερο να κινηθεί. Αυτός καθώς κινείται παραμένει διαρκώς οριζόντιος και πριν να εξέλθει από το ομογενές μαγνητικό πεδίο αποκτά ταχύτητα σταθερού μέτρου.
Δ4. Να ελέγξετε, αν τότε, η συσκευή λειτουργεί κανονικά. (Μονάδες 5)
Δ5. Τη χρονική στιγμή που ο αγωγός ΚΛ κινείται με ταχύτητα μέτρου ίσου με το μισό του μέτρου της σταθερής ταχύτητας που αποκτά, να υπολογίσετε το ρυθμό μεταβολής της μηχανικής ενέργειάς του.
(Μονάδες 5)
Δίνεται g=10m/s².
Με τις καλλίτερες ευχές για εκπλήρωση κάθε υψηλού και ωραίου στις Πανελλήνιες εξετάσεις

ΘΕΜΑ Γ

Γ1.   επειδή δημιουργούνται  5  ακίνητα σημεία  (τα 2 είναι τα άκρα Δ και Γ)  έχουμε  2 ατράκτους  δηλαδή  2 μήκη κύματος  (ΔΓ) = 2 λ = 2 l = 4 m               συνφ = (ΑΓ) / (ΔΓ) = 2m / 4m  =  0,5  =>  φ = 60°

  ισορροπία Σ₁    m₁ g = T_ν2 =  10 Ν 

  ισορροπία δοκού  ροπές ως προς Α : 

  - Τ_ν2 (ΑΓ)  -  Mg  (ΑΓ)/2  +  Τ_ν1 ημφ  =  0   =>  - 10Ν  2m  -  Mg  1m  +  Μg√3  √3/2  2m  =  0   =>

    =>  - 20  -  Mg  +  Μg 3  =  0  =>  Mg = 10  =>  M = 1 kg   μάζα δοκού ΑΓ

Γ2.    ισορροπία δοκού  ροπές ως προς Α : 

  - Τ_ν2 (ΑΓ)  -  Mg  (ΑΓ)/2   -   mg x  +  Τ_ν1 ημφ  =  0   =>   - 10N  2m  -  10N  1m   -   20 x  +   20√3  √3/2  2m  =  0   =>

   =>   - 20  -  10   -   20 x  +   60  =  0   =>  x = 1,5 m      

Γ3.     ισορροπία Σ₂    m₂ g  =  k Δl  =>  10  =  100  Δl  =>  Δl = 0,1 m    συσπείρωση ελατηρίου    

  k = m₂ ω² =>  100 = 1  ω²  =>  ω = 10 rad/s        f = 10/2π = 5/π Hz     T = π/5 s

διατήρηση ενέργειας  για την ταλάντωση   ½ k  Δl ²  +  ½ m v₀²  =  ½ k  A²  =  ½  m v_max²  => 

   =>  100  0,1 ²  +   1  (√3)²  =  1000  A²  =  1 v_max²  =>  1  +  3  = 100  A²  =  v_max²  =>

   =>  1  +  3  =  100  A²  =  v_max²  =>  A² =  4/100 = 0,04  =>  A = 0,2 m     

   v_max = √4 m/s  =  2 m/s   v_max = 2 m/s  

 x(t) = 0,2 ημ(10.t + π/2)        v(t) = 2 συν(10.t + π/2)        α(t) = - 20 ημ(10.t + π/2)  

Γ4.     το Σ₁  κατεβαίνει με επιτάχυνση g   διανύοντας απόσταση  y    και   το Σ₂ είναι σε απομάκρυνση x   

   h =  ½ g t²   =>  ½  10  t²  =  0,2  =>  t²  =  0,04  =>  t = 0,2 s    

    v₁ = g t = 10  0,2  m/s =  2 m/s    προς τα κάτω  

επειδή οι ταχύτητες των σωμάτων είναι αντίθετες  συμπεραίνουμε ότι  το Σ₁  κατέρχεται με 2m/s  ενώ το Σ₁  ανέρχεται με 2m/s     

  κεντρική πλαστική κρούση :   m₁ v₁  +  m₂ v₂  =  (m₁ + m₂) u  =>  1 kg  2 m/s  + 1 kg  (- 2 m/s)  =  2 kg  u  =>  u = 0  

  θέση ισορροπίας συσσωματώματος :  (m₁ + m₂) g  =  k  x₀  =>  2 kg  10 m/s²  = 100 N/m  x₀  => x₀ = 0,2 m 

  (m₁ + m₂) ω²  =  k  =>  2  ω²  =  100  =>  ω = √50 rad/s  =  5√2 rad/s 

  η κρούση γίνεται στη θέση ισορροπίας του Σ₂  ( 0,1m υψηλότερα από τη θέση ισορροπίας του συσσωματώματος )  όταν αυτό ανέρχεται,   

  μετά την κρούση το συσσωμάτωμα ακινητοποιείται στιγμιαία  0,1m υψηλότερα από τη θέση ισορροπίας του

    x =  0,1 ημ(5√2.t + π/2)         v =  0,5√2 συν(5√2.t + π)       α = - 5 ημ(10√5.t + π) 

ΘΕΜΑ Γ

Γ1.   επειδή δημιουργούνται  5  ακίνητα σημεία  (τα 2 είναι τα άκρα Δ και Γ)  έχουμε  2 ατράκτους  δηλαδή  2 μήκη κύματος  (ΔΓ) = 2 λ = 2 l = 4 m               συνφ = (ΑΓ) / (ΔΓ) = 2m / 4m  =  0,5  =>  φ = 60°

  ισορροπία Σ₁    m₁ g = T_ν2 =  10 Ν 

  ισορροπία δοκού  ροπές ως προς Α : 

  - Τ_ν2 (ΑΓ)  -  Mg  (ΑΓ)/2  +  Τ_ν1 ημφ  =  0   =>  - 10Ν  2m  -  Mg  1m  +  Μg√3  √3/2  2m  =  0   =>

    =>  - 20  -  Mg  +  Μg 3  =  0  =>  Mg = 10  =>  M = 1 kg   μάζα δοκού ΑΓ

Γ2.    ισορροπία δοκού  ροπές ως προς Α : 

  - Τ_ν2 (ΑΓ)  -  Mg  (ΑΓ)/2   -   mg x  +  Τ_ν1 ημφ  =  0   =>   - 10N  2m  -  10N  1m   -   20 x  +   20√3  √3/2  2m  =  0   =>

   =>   - 20  -  10   -   20 x  +   60  =  0   =>  x = 1,5 m      

Γ3.     ισορροπία Σ₂    m₂ g  =  k Δl  =>  10  =  1000  Δl  =>  Δl = 0,01 m = 1 cm   συσπείρωση ελατηρίου    

  k = m₂ ω² =>  1000 = 1  ω²  =>  ω = 10√10 rad/s = 10π rad/s        f = 10π/2π = 5 Hz     T = 1/5 s = 0,2 s

διατήρηση ενέργειας  για την ταλάντωση   ½ k  Δl ²  +  ½ m v₀²  =  ½ k  A²  =  ½  m v_max²  => 

   =>  1000  0,01 ²  +   1  (√3/π)²  =  1000  A²  =  1 v_max²  =>   0,1  +  3/π²  = 1000  A²  =  v_max²  =>

   =>  0,1  +  3/10  =  1000  A²  =  v_max²  =>  A² =  0,4/1000 = 0,0004  =>  A = 0,02 m     

   v_max = √0,4 m/s  = √(4/10) m/s  =  2/√10 m/s  = 2/π m/s =  2π/π² m/s =  2π/10 m/s => v_max = 0,2π m/s  

 x(t) = 0,02 ημ(10π.t + π/2)        v(t) = 0,2π συν(10π.t + π/2)        α(t) = - 20 ημ(10π.t + π/2)  

Γ4.     το Σ₁  κατεβαίνει με επιτάχυνση g   διανύοντας απόσταση  y    και   το Σ₂ είναι σε απομάκρυνση x   

   h =  ½ g t²   =>  ½  10  t²  =  5/4  =>  t²  = 1/4  =>  t = 0,5 s    

    v₁ = g t = 10  0,5  m/s = 5 m/s    προς τα κάτω 

  x( 0,5 )  =  0,02 ημ(10π. 0,5 + π/2)  =  0,02 ημ(5π + π/2)  =  0,02  (-1)  = - 0,02 m    κάτω ακραία θέση ταλάντωσης Σ₂ 

  v( 0,5 )  =  0,2π συν(10π. 0,5  + π/2)  =  0,2π συν(5π + π/2)  =  0  

  κεντρική πλαστική κρούση :   m₁ v₁  +  m₂  0  =  (m₁ + m₂)  u  =>  1 kg  5 m/s  =  2 kg  u  =>  u = 2,5 m/s   προς τα κάτω

  θέση ισορροπίας συσσωματώματος :  (m₁ + m₂) g  =  k  x₀  =>  2 kg  10 m/s²  =  1000 N/m  x₀  =>  x₀  =  0,02 m 

  (m₁ + m₂) ω²  =  k  =>  2  ω²  =  1000  =>  ω = √500 rad/s  =  10√5 rad/s 

  η θέση ισορροπίας του συσσωματώματος  συμπίπτει με την κάτω ακραία θέση της ταλάντωσης του Σ₂  εκεί όπου έγινε η πλαστική κρούση   συνεπώς το συσσωμάτωμα θα αρχίσει να ταλαντώνεται από τη θέση ισορροπίας του  με αρχική ταχύτητα 2,5 m/s  προς τα κάτω   επειδή η θετική φορά είναι προς τα πάνω 

   v =  2,5  συν(10√5.t + π)         x =  2,5/10√5  ημ(10√5t + π) =  √5/20  ημ(10√5.t + π)    

    α = - 25√5  ημ(10√5.t + π) 

η ράβδος κινείται μέσα στο μαγνητικό πεδίο  οπότε στα άκρα της αναπτύσσεται επαγωγική τάση :

  Ε_επ = B l v = 0,01 T  1 m  √5/20  ημ(10√5.t + π)  =  √5/2000  ημ(10√5.t + π)  (Volt)  

 το επαγωγικό ρεύμα :  i = B l v / (R + R_V)   επειδή το βολτόμετρο είναι ιδανικό η ένταση του ρεύματος θα είναι αμελητέα  οπότε η τάση στα άκρα του βολτομέτρου θα είναι ίση με την επαγωγική τάση 

η ένδειξη του βολτομέτρου ισούται με την ενεργό ταση :  V_V =  √5/2000 / √2  =  √10/4000  Volt

ΘΕΜΑ Δ

 αντίσταση συσκευής :  R_Σ =  8² / 16 = 4 Ω     ρεύμα κανονικής λειτουργίας :  i_Σ = 8 / 4 = 2 Α 

  κλείνουν οι διακόπτες  η συσκευή διαρρέεται από  2 Α  καθώς και η ράβδος από  2 Α  διότι είναι σε παρράληλη σύνδεση και έχουν ίσες αντιστάσεις   το συνολικό ρεύμα είναι  4 Α  ενεργός τιμή  το πλάτος του είναι  4√2 Α    η συνολική αντίσταση είναι R_ολ = 4 4 / (4+4) = 2 Ω     το πλάτος της τάσης είναι  V = 4√2 A  2 Ω  =  8√2 Volt   

       μέση ισχύς  Ρ_Μ =  i_εν² R_ολ  =  4²  2  =  32 Watt  

   V(t) = 8√2 ημ(100π.t)     i(t) = 4√2 ημ(100π.t)      P(t) = V(t)  i(t)  =  64 ημ²(100π.t)  

  η ράβδος διαρρέεται από ρεύμα  i(t) = 2√2 ημ(100π.t)   και η συσκευή από  i(t) = 2√2 ημ(100π.t) 

  i(0,1325)  =  2√2 ημ(100π.0,1325)  =  2√2 ημ(13,25 π)  =  2√2 (- √2/2) = - 2 A    αντίθετη κατεύθυνση    F =  mg  +  F_L =  mg  +   B l i =  0,05  10   +  0,5   1   2  =>  F = 1,5 N    η F_L κατακόρυφη προς τα κάτω  ομόρροπη του βάρους      ενώ  η F κατακόρυφη προς τα πάνω 

  ανοίγουμε τον δ₁   καταργείται η F    η ράβδος  κινείται στο μαγνητικό πεδίο  εμφανίζεται επαγωγική τάση  Ε_επ = B l v  =  i (R_Σ + R) =>  0,5  1  v  =  i  8  =>  i =  v/16            

  mg  -  B l i  =  m a  =>  0,05  10  -  0,5  1  v/16  =  0,05  a  =>  a  =  10  -  5v/8         

  a = 0  =>  v_ορ = 16 m/s      i =  1 A    η συσκευή  υπολειτουργεί 

 v = 8 m/s    a = 10  -  5  =  5 m/s²          i = v/16 = 8/16 = 0,5 A       F_L = B l i =  0,5 T  1 m  0,5 A = 0,25 N

   P_FL =  F_L  v συν180°  =  - 0,25 N  8 m/s  =  - 2 J/s 

   dK/dt = m v a =  0,05 kg  8 m/s  5 m/s²  =  2 J/s       

  dU/dt  =  - mg v  =  - 0,05 kg  10 m/s²   8 m/s  =  - 4 J/s           dW_w/dt  mg v  =  4 J/s

  dE/dt  =  dK/dt  +  dU/dt  =  2 J/s  +  (- 4 J/s)  =  - 2 J/s   ρυθμός μεταβολής της μηχανικής ενέργειας