παγκύπριες εξετάσεις

2025

Ερώτηση 1
Η Γραφική Παράσταση δείχνει τη μετατόπιση ενός αρμονικού ταλαντωτή από τη θέση ισορροπίας του ως συνάρτηση του χρόνου, 𝑦 = 𝑓(𝑡).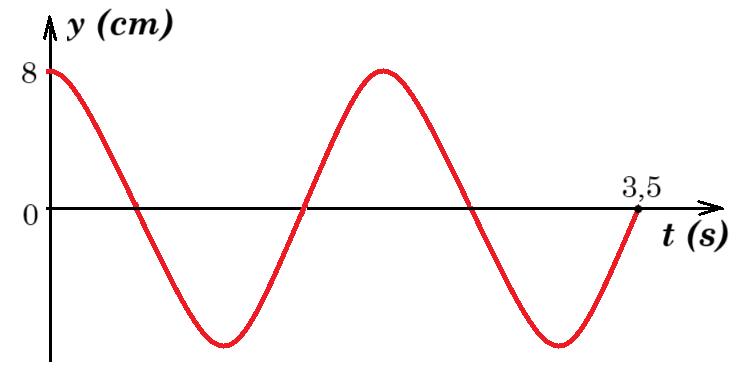

(α) Να χρησιμοποιήσετε τη Γραφική Παράσταση για να γράψετε την εξίσωση της μετατόπισης σε σχέση με τον χρόνο. (3 μονάδες)
(β) Η μάζα 𝑚 του αρμονικού ταλαντωτή είναι 20 g. Να υπολογίσετε το μέτρο της μέγιστης συνισταμένης δύναμης που ασκείται στη μάζα. (2 μονάδες)

Ερώτηση 4
Η κεραία της τηλεόρασης λαμβάνει ραδιοκύματα και η συσκευή της τηλεόρασης λαμβάνει υπέρυθρα κύματα από το τηλεχειριστήριο, κάθε φορά που ο χρήστης επιχειρεί κάποια αλλαγή στη λειτουργία της. Επίσης, η τηλεόραση εκπέμπει ορατό φως από την οθόνη και ηχητικά κύματα από τα ηχεία της. Τα κύματα διακρίνονται σε Μηχανικά και Ηλεκτρομαγνητικά Κύματα.
(α) Να αναφέρετε ποια από τα κύματα που αναφέρονται παραπάνω είναι μηχανικά.
(1 μονάδα)
(β) Από τα προαναφερθέντα Ηλεκτρομαγνητικά Κύματα, να αναφέρετε:
i. ποιος τύπος κύματος έχει τη μεγαλύτερη συχνότητα, (1 μονάδα)
ii. ποιος τύπος κύματος έχει το μεγαλύτερο μήκος κύματος, (1 μονάδα)
iii. ποιος τύπος κύματος παρουσιάζει εντονότερο φαινόμενο περίθλασης από ένα ψηλό κτήριο. (1 μονάδα)
(γ) Να γράψετε δύο από τα προαναφερθέντα κύματα που γίνονται αντιληπτά από τις αισθήσεις των ανθρώπων. (1 μονάδα)

Ερώτηση 5
Η Εικόνα παρουσιάζει μια πόρτα πλάτους 𝐿 = 90 cm, η οποία μπορεί να περιστρέφεται γύρω από κατακόρυφο, ακλόνητο άξονα. Στην πόρτα ασκούνται τρεις δυνάμεις με μέτρα |𝐹⃗1| = 10 Ν, |𝐹⃗2| = 5 Ν και |𝐹⃗3| = 6 N, και κοινό σημείο εφαρμογής το σημείο Ο.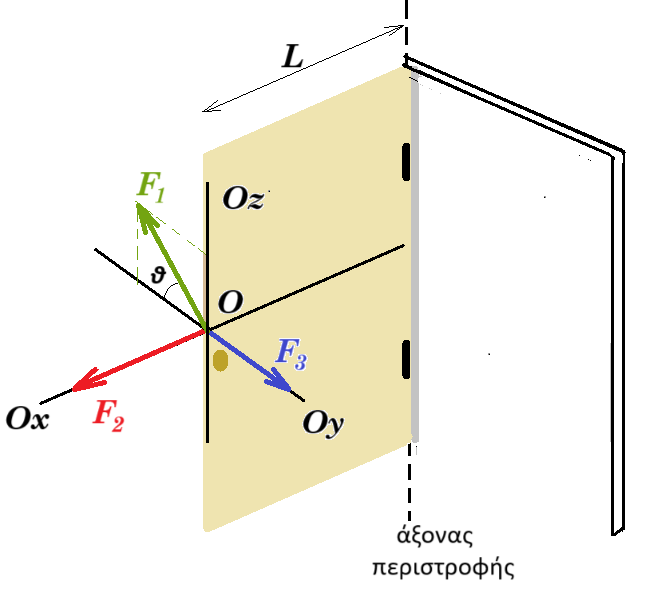 Οι δυνάμεις 𝐹⃗2 και 𝐹⃗3 έχουν την κατεύθυνση του άξονα Ο𝑥 και Ο𝑦, αντίστοιχα. Η 𝐹⃗1
βρίσκεται στο επίπεδο 𝑦𝑧 και σχηματίζει γωνία 𝜃 = 60° με τον άξονα των 𝑦. Ο άξονας περιστροφής της πόρτας είναι παράλληλος με τον άξονα των 𝑧.
(α) Να υπολογίσετε την αλγεβρική τιμή της ροπής της κάθε δύναμης κατά μήκος του άξονα περιστροφής της πόρτας. (3 μονάδες)
(β) Να εξηγήσετε προς ποια φορά οι δυνάμεις αυτές τείνουν να περιστρέψουν την πόρτα (αριστερόστροφα ή δεξιόστροφα). (2 μονάδες)

Ερώτηση 7
Η πιο κάτω εξίσωση περιγράφει ένα τρέχον αρμονικό κύμα που διαδίδεται σε γραμμικό ελαστικό μέσο 𝑦(𝑥, 𝑡) = (8,0 mm) ημ [2𝜋 ((5,0 s-1) 𝑡 - 2,0𝑥m)]
(α) Να υπολογίσετε την ταχύτητα διάδοσης του κύματος. (2 μονάδες)
(β) Τη χρονική στιγμή 𝑡 = 0 ξεκινά η ταλάντωση της πηγής του κύματος, η οποία βρίσκεται στη θέση 𝑥 = 0. Να σχεδιάσετε, σε βαθμονομημένους άξονες στο χιλιοστομετρικό χαρτί, το στιγμιότυπο του κύματος τη χρονική στιγμή 𝑡 = 0,25 s. (3 μονάδες)

Ερώτηση 10
Η Εικόνα παρουσιάζει μια τροχαλία, μάζας 𝑀 και ακτίνας 𝑅, η οποία μπορεί να περιστρέφεται γύρω από έναν σταθερό οριζόντιο άξονα χωρίς τριβές. Ένα αβαρές σχοινί είναι περιτυλιγμένο γύρω από την τροχαλία και ένα σώμα μάζας 𝑚 = 𝛭/4 είναι
προσαρτημένο στο άκρο του σχοινιού.
Το σύστημα συγκρατείται αρχικά σε ηρεμία και στη συνέχεια το σώμα αφήνεται να κατέλθει. Το τυλιγμένο σχοινί περιστρέφεται μαζί με την τροχαλία χωρίς να ολισθαίνει ως προς αυτή. Η ροπή αδράνειας της τροχαλίας ως προς τον άξονα περιστροφής της είναι 𝛪τρ = 1/2 𝛭𝑅².

(α) Να δείξετε ότι το μέτρο της γωνιακής επιτάχυνσης της τροχαλίας είναι: |𝑎⃗𝛾| = g/3𝑅
(3 μονάδες)
(β) Η μάζα του σώματος είναι 𝑚 = 12 kg και η ακτίνα της τροχαλίας είναι 𝑅 = 0,20 m.
Nα υπολογίσετε το μέτρο της γωνιακής ταχύτητας της τροχαλίας όταν το σώμα έχει κατέλθει κατά Δℎ = 0,50 m. (2 μονάδες)

Ερώτηση 14
(α) Να αναφέρετε τις προϋποθέσεις για τη δημιουργία ενός στάσιμου κύματος. (2 μονάδες)
(β) Σε μια δεξαμενή κυματισμών δύο σύμφωνες σημειακές πηγές, Α και Β, ταλαντώνονται στην κατακόρυφη διεύθυνση 𝑦 με το ίδιο πλάτος ταλάντωσης και δημιουργούν στην επιφάνεια του νερού κυκλικά κύματα. Στη Γραφική Παράσταση παρουσιάζεται ένα στιγμιότυπο τμήματος του στάσιμου κύματος που δημιουργείται πάνω στην ευθεία μεταξύ των δύο πηγών Α και Β, για -10 cm < 𝑥 < +10 cm. Η αρχή των αξόνων 𝛰 βρίσκεται στο μέσο των δύο πηγών.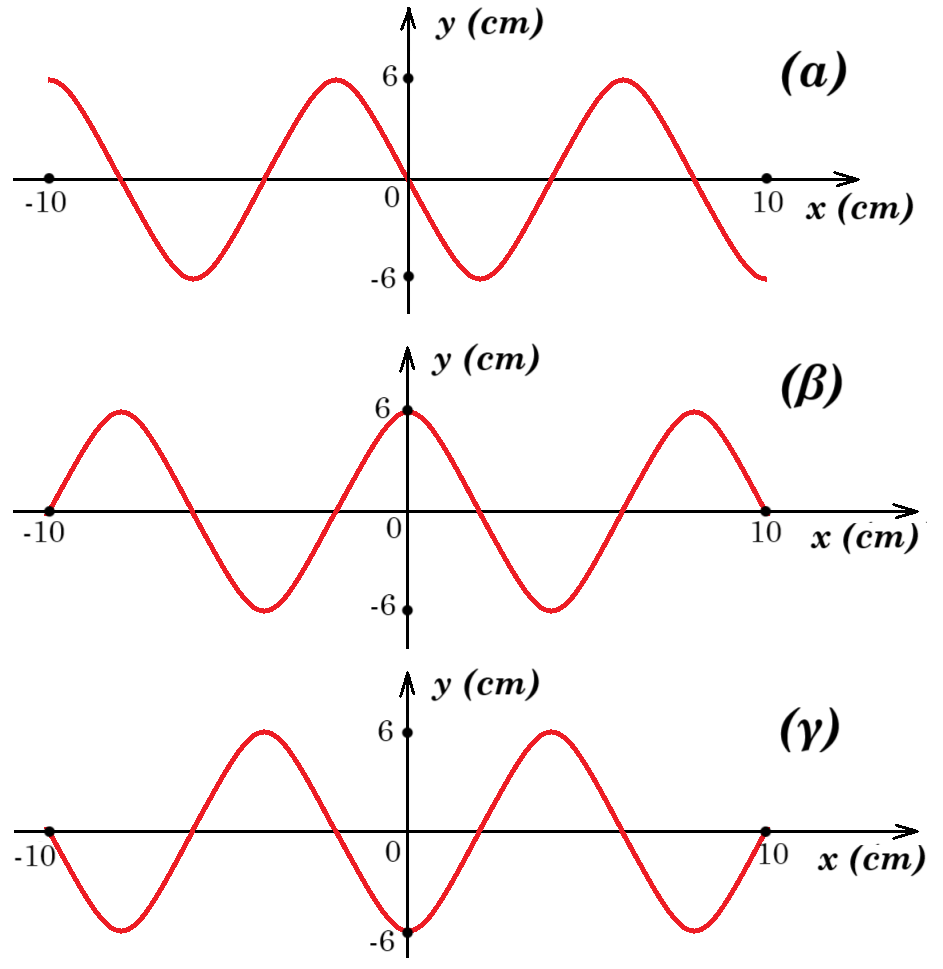 i. Να εξηγήσετε κατά πόσον οι δύο πηγές έχουν μηδενική διαφορά φάσης ή έχουν διαφορά φάσης 𝜋 rad. (2 μονάδες)
ii. Να υπολογίσετε τον αριθμό των υπερβολών καταστροφικής συμβολής και τον αριθμό των υπερβολών ενισχυτικής συμβολής που δημιουργούνται στην επιφάνεια της δεξαμενής και τέμνουν τον άξονα των 𝑥, για -10 cm < 𝑥 < +10 cm. (2 μονάδες)
iii. Εάν η ταχύτητα διάδοσης των κυμάτων που δημιουργούν οι δύο πηγές είναι 5 m/s να υπολογίσετε τη συχνότητα των πηγών. (2 μονάδες)
iv. Η ταχύτητα διάδοσης των κυμάτων εξαρτάται από το βάθος του νερού: όσο πιο βαθύ είναι το νερό, τόσο μεγαλύτερη είναι η ταχύτητα διάδοσης. Να εξηγήσετε πώς θα μεταβληθεί ο αριθμός των υπερβολών συμβολής, εάν για τις ίδιες πηγές 𝛢 και 𝛣 (χωρίς να μεταβάλουμε τη συχνότητα ή την απόσταση των πηγών), μειώσουμε αρκετά το βάθος του νερού στη δεξαμενή κυματισμών. (2 μονάδες)

Ερώτηση 15
Ένα πηνίο περιστρέφεται με σταθερή συχνότητα μέσα σε ομογενές μαγνητικό πεδίο, ως προς άξονα που είναι κάθετος στη σελίδα. Το πηνίο αποτελείται από 500 σπείρες, καθεμιά από τις οποίες έχει εμβαδόν 2,5 × 10^-3m².
Η Γραφική Παράσταση παρουσιάζει πώς μεταβάλλεται η μαγνητική ροή στο εσωτερικό του πηνίου με τον χρόνο.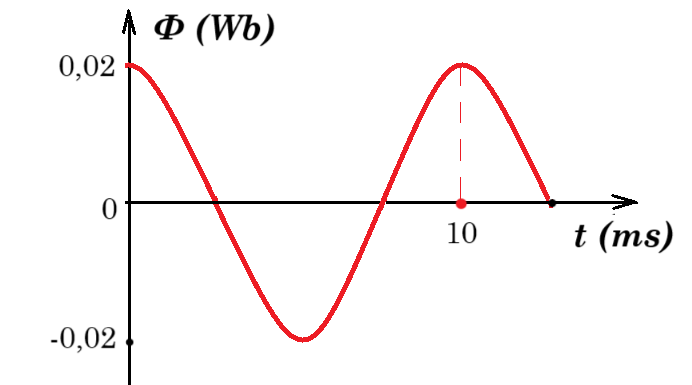
(α) Να υπολογίσετε τον αριθμό των περιστροφών ανά λεπτό που κάνει το πηνίο. (2 μονάδες)
(β) Να προσδιορίσετε τo μέτρο της έντασης του μαγνητικού πεδίου. (2 μονάδες)
(γ) i. Να υπολογίσετε τη μέγιστη τιμή της επαγόμενης ηλεκτρεγερτικής δύναμης (ΗΕΔ) που δημιουργείται από την περιστροφή του πηνίου. (3 μονάδες)
ii. Να σχεδιάσετε, για το χρονικό διάστημα 0 ≤ 𝑡 ≤ 10 ms, το γράφημα της επαγόμενης ΗΕΔ σε συνάρτηση με τον χρόνο. (2 μονάδες)

14 οι πηγές κυμάτων είναι σύμφωνες δηλαδή έχουν σταθερή διαφορά φάσης Δφ
(α) τα κύματα φθάνουν στο μέσον της απόστασης των πηγών Α και Β στη θέση x=0 το οποίο παρατηρούμε ότι έχει απομάκρυνση y=0 δηλαδή είναι δεσμός συνεπώς οι πηγές έχουν διαφορά φάσης Δφ = π rad (φθάνει μέγιστο (όρος) από τη μία πηγή και ελάχιστο από την άλλη (κοιλάδα) )

δημιουργούνται 4 υπερβολές ενισχυτικής συμβολής και 5 υπερβολές καταστροφικής συμβολής

λ = 8 cm 2A = 6 cm => A = 3 cm v = λ f => 5 m/s = 0,08 m f => f = 62,5 Hz

T = 0,016 s = 2/125 s

μειώνουμε το βάθος του νερού άρα μειώνεται η ταχύτητα του κύματος συνεπώς μειώνεται το μήκος κύματος άρα αυξάνεται το πλήθος των υπερβολών συμβολής

εξίσωση στασίμου κύματος : y = - 0,06 ημ(2πx/0,08) = - 0,06 ημ(25πx) - 0,1 m £ x £ +0,1 m

εξίσωση κύματος από τις πηγές

y₁ (x,t) = 0,03 ημ(2π 62,5 t - 2π(x+0,1)/0,08 + π) = 0,03 ημ(125π.t - 25π.(x+0,1) + π)

y₂ (x,t) = 0,03 ημ(2π 62,5 t + 2π(x-0,1)/0,08) = 0,03 ημ(125π.t + 25π.(x-0,1))

y = y₁ + y₂ = 0,03 2 ημ[ 125π.t - 25π.(x+0,1) + π + 125π.t + 25π.(x-0,1) ] / 2

συν [ 125π.t - 25π.(x+0,1) + π - 125π.t - 25π.(x-0,1) ] / 2 =

= 0,06 ημ[ 125π.t - 2π ] συν [ - 25π.x + π/2 ] = 0,06 ημ(25π.x) ημ(125π.t)

ημ(125π.t) = - 1 = ημ(3π/2) => 125π.t = 2κπ + 3π/2 => t = 2κ/125 + 3/250 κ = 0, 1, 2, 3, ...

κ = 0 t = 3/250 s = 0,012 s

κ = 1 t = 5/250 s = 0,02 s

κ = 2 t = 7/250 s = 0,028 s

κ = 3 t = 9/250 s = 0,036 s

κ = 4 t = 11/250 s = 0,044 s δεκτή λύση

κ = 5 t = 13/250 s = 0,052 s δεκτή λύση

(β) τα κύματα φθάνουν στο μέσον της απόστασης των πηγών Α και Β στη θέση x=0 το οποίο παρατηρούμε ότι έχει μέγιστη απομάκρυνση y=+6cm δηλαδή είναι κοιλία συνεπώς οι πηγές έχουν διαφορά φάσης Δφ = 0 rad (φθάνει μέγιστο (όρος) από τη μία πηγή και μέγιστο από την άλλη (όρος) )

δημιουργούνται 5 υπερβολές ενισχυτικής συμβολής και 4 υπερβολές καταστροφικής συμβολής

εξίσωση στασίμου κύματος : y = 0,06 συν(2πx/0,08) = 0,06 συν(25πx) - 0,1 m £ x £ +0,1 m

τη στιγμή t = 0 φεύγουν τα κύματα από τις δύο πηγές

το κύμα από την πηγή στη θέση x = - 0,1 m για να πάει στη θέση x = + 0,1 m θέλει χρόνο t = 0,2 m / 5 m/s = 0,04 s και το αντίστροφο από την πηγή στη θέση x = + 0,1 m για να πάει στη θέση x = - 0,1 m

εξίσωση κύματος από τις πηγές

y₁ (x,t) = 0,03 ημ(2π 62,5 t - 2π(x+0,1)/0,08) = 0,03 ημ(125π.t - 25π.(x+0,1))

y₂ (x,t) = 0,03 ημ(2π 62,5 t + 2π(x-0,1)/0,08) = 0,03 ημ(125π.t + 25π.(x-0,1))

y = y₁ + y₂ = 0,03 2 ημ[ 125π.t - 25π.(x+0,1) + 125π.t + 25π.(x-0,1) ] / 2

συν [ 125π.t - 25π.(x+0,1) - 125π.t - 25π.(x-0,1) ] / 2 =

= 0,06 ημ(125π.t - 2,5π) συν(- 25π.x) = 0,06 συν(25π.x) ημ(125π.t - 2,5π)

ημ(125π.t - 2,5π) = 1 => 125π.t - 2,5π = 2κπ + π/2 => 125π.t = 2κπ + π/2 + 2,5π = 2κπ + 3π =>

=> t = 2κ/125 + 3/125 κ = 0, 1, 2, 3, ...

κ = 0 t = 3/125 s = 0,008 s απορρίπτεται διότι < 0,04 s

κ = 1 t = 2/125 + 3/125 s = 5/125 s = 0,04 s =ο αναγκαίος χρόνος για να φθάσουν τα κύματα και να δημιουργηθεί το στάσιμο κύμα (β)

κ = 2 t = 4/125 + 3/125 s = 7/125 s = 0,056 s = 0,04 s + 0,016 s = 0,04 s + T

κ = 3 t = 6/125 + 3/125 s = 9/125 s = 0,072 s = 0,04 s + 0,032 s = 0,04 s + 2T

κ = 4 t = 8/125 + 3/125 s = 11/125 s = 0,088 s = 0,04 s + 0,048 s = 0,04 s + 3T

(γ) τα κύματα φθάνουν στο μέσον της απόστασης των πηγών Α και Β στη θέση x=0 το οποίο παρατηρούμε ότι έχει μέγιστη απομάκρυνση y=-6cm δηλαδή είναι κοιλία συνεπώς οι πηγές έχουν διαφορά φάσης Δφ = 0 rad (φθάνει ελάχιστο (κοιλάδα) από τη μία πηγή και ελάχιστο από την άλλη (κοιλάδα) )

δημιουργούνται 5 υπερβολές ενισχυτικής συμβολής και 4 υπερβολές καταστροφικής συμβολής

εξίσωση στασίμου κύματος : y = - 0,06 συν(2πx/0,08) = - 0,06 συν(25πx) - 0,1 m £ x £ +0,1 m

εξίσωση κύματος από τις πηγές

y₁ (x,t) = 0,03 ημ(2π 62,5 t - 2π(x+0,1)/0,08) = 0,03 ημ(125π.t - 25π.(x+0,1))

y₂ (x,t) = 0,03 ημ(2π 62,5 t + 2π(x-0,1)/0,08) = 0,03 ημ(125π.t + 25π.(x-0,1))

y = y₁ + y₂ = 0,03 2 ημ[ 125π.t - 25π.(x+0,1) + 125π.t + 25π.(x-0,1) ] / 2

συν [ 125π.t - 25π.(x+0,1) - 125π.t - 25π.(x-0,1) ] / 2 =

= 0,06 ημ(125π.t - 2,5π) συν(- 25π.x) = 0,06 συν(25π.x) ημ(125π.t - 2,5π)

ημ(125π.t - 2,5π) = - 1 => 125π.t - 2,5π = 2κπ + 3π/2 => 125π.t = 2κπ + 3π/2 + 2,5π = 2κπ + 4π => t = 2κ/125 + 4/125 κ = 0, 1, 2, 3, ...

κ = 0 t = 4/125 s = 0,032 s απορρίπτεται διότι < 0,04 s

κ = 1 t = 2/125 + 4/125 s = 6/125 s = 0,048 s = 0,04 s + 0,008 s = 0,04 s + T/2

κ = 2 t = 4/125 + 4/125 s = 8/125 s = 0,064 s = 0,04 s + 0,024 s = 0,04 s + 3T/2

κ = 3 t = 6/125 + 4/125 s = 10/125 s = 0,08 s = 0,04 s + 0,04 s = 0,04 s + 5T/2

2024

Ερώτηση 14
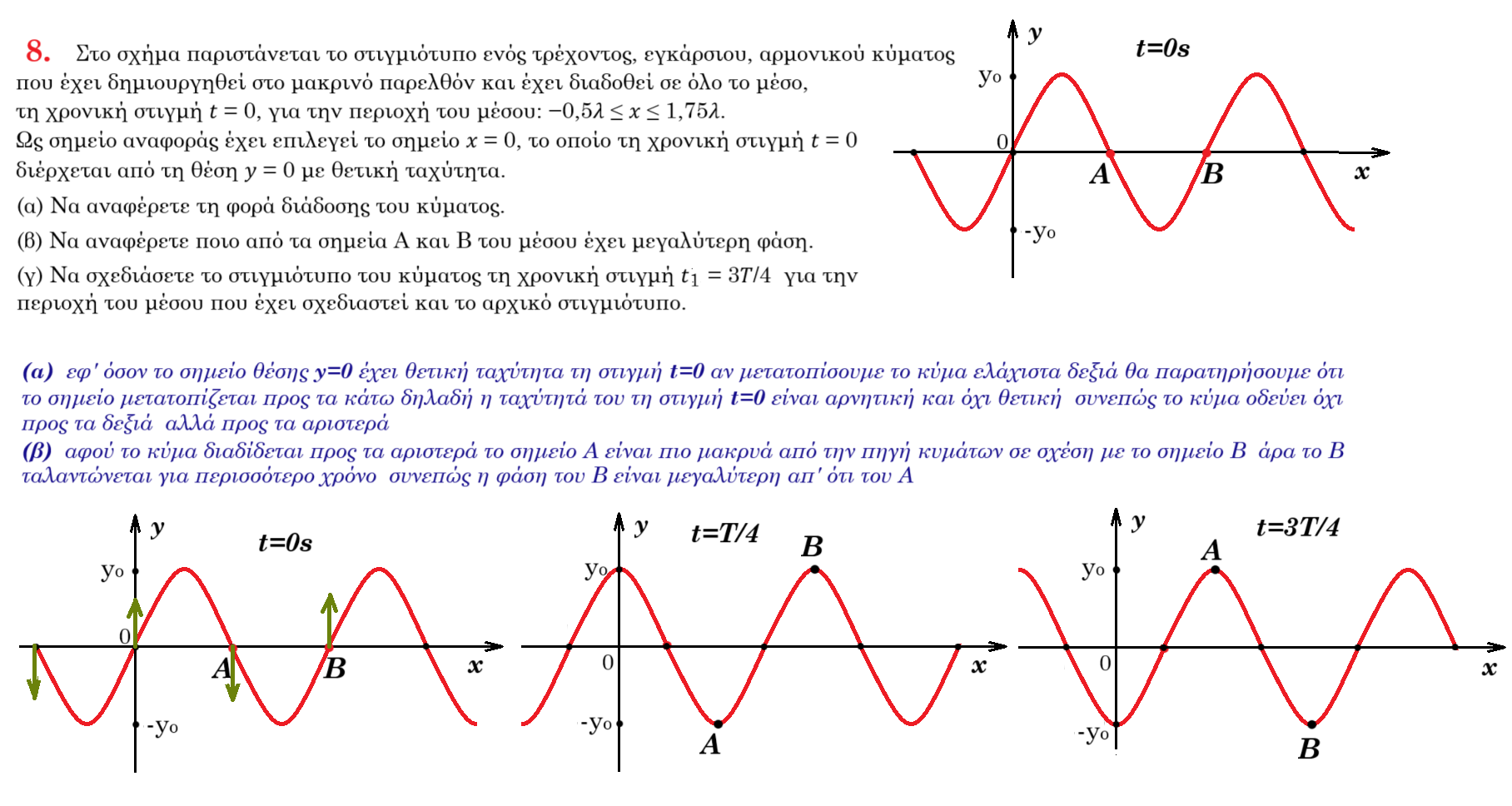
Κατά μήκος μιας ελαστικής χορδής διαδίδεται εγκάρσιο αρμονικό κύμα. Το κύμα διαδίδεται κατά τη θετική φορά και η διάδοσή του ξεκίνησε τη στιγμή 𝑡0 = 0. Στο πιο κάτω σχήμα φαίνεται η γραφική παράσταση της μετατόπισης από τη θέση ισορροπίας, σε σχέση με τον χρόνο, ενός σημείου Α της χορδής. Το σημείο Α απέχει απόσταση 0,4 m από την πηγή του κύματος, η οποία βρίσκεται στη θέση 𝑥 = 0.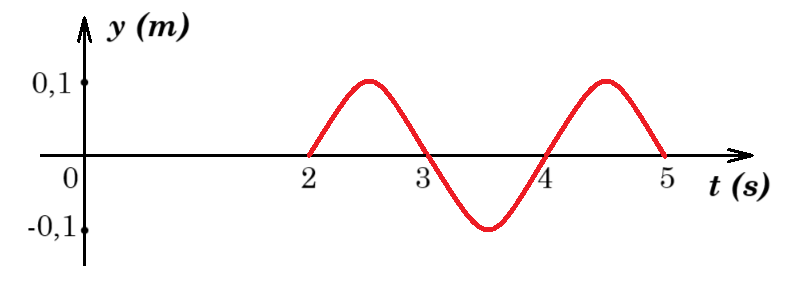

(α) Να υπολογίσετε την ταχύτητα διάδοσης του κύματος. (1 μονάδα)
(β) Να υπολογίσετε το μήκος του κύματος. (2 μονάδες)
(γ) Να υπολογίσετε τη διαφορά φάσης μεταξύ του σημείου Α και της πηγής του κύματος. (1 μονάδα)

(δ) Να γράψετε την εξίσωση που περιγράφει τη μετατόπιση του σημείου Α από τη θέση ισορροπίας του, σε συνάρτηση με το χρόνο. (1 μονάδα)

(ε) Να σχεδιάσετε στο τετραγωνισμένο χαρτί το στιγμιότυπο του κύματος τη χρονική στιγμή 𝑡 = 4,5 s. (2 μονάδες)

(στ) Να γράψετε την εξίσωση ενός άλλου κύματος που διαδίδεται στην ίδια χορδή, προς την ίδια κατεύθυνση, με το ίδιο πλάτος και διπλάσια συχνότητα από το αρχικό. (3 μονάδες)

10.

Στ_{στήριγμα} = 0 => Mg l/4 - mg l/4 + F_Lapl l/4 = 0 =>

=> 5m g - mg + F_Lapl = 0 => F_Lapl = - 4mg κατακόρυφη προς τα κάτω ομόρροπη του βαρους της ράβδου

F_Lapl = B i l => i = 4mg / Bl

13.

λ/2 = 2 cm => λ = 0,04 m v = 0,04 m 40 Hz = 1,6 m/s

ΡΠ₁ - ΡΠ₂ = 3λ - 2λ = 0,04 m

14.

x_A = 0,4 m t_A = 2 s v_δ = 0,4m / 2s = 0,2 m/s

Τ = 2s f = 0,5 Hz λ = v_δ Τ = 0,2 2 = 0,4 m

Δφ = 2π Δx / λ = 2π 0,4 / 0,4 = 2π rad

y_A = 0,1 ημ2π(t/2 - 0,4/0,4) = 0,1 ημ(πt - 2π) = 0,1 ημ(πt)

y = 0,1 ημ2π(t/2 - x/0,4) => y = 0,1 ημ(πt - 5πx)

t = 4,5 s = 2T + T/2 y = 0,1 ημ(4,5π - 5πx)

f ' = 1 Hz T ' = 1 s λ' = v_δ Τ ' = 0,2 1 = 0,2 m

y' = 0,1 ημ2π(t/1 - x/0,2) => y' = 0,1 ημ(2πt - 10πx)

15.

x_A = 0,4 m t_A = 2 s v_δ = 0,4m / 2s = 0,2 m/s

ΣF_x = 0 => F_Γx - T_x = 0 => F_Γx = T 0,6

Στ_(Γ) = 0 => mg l/2 = T 0,8 l => 20 / 2 = T 0,8 => T = 100/8 N = 12,5 N

dL/dt = Στ_(Γ) = mg l/2 = 20 3/2 = 30 N.m

mg l/2 = ½ I ω² => 20 3/2 = 0,5 1/3 2 3² ω² => ω² = 10 => ω = 10^½

υ_Γ = ω l = 3 10^½ m/s

2021

2020

2019

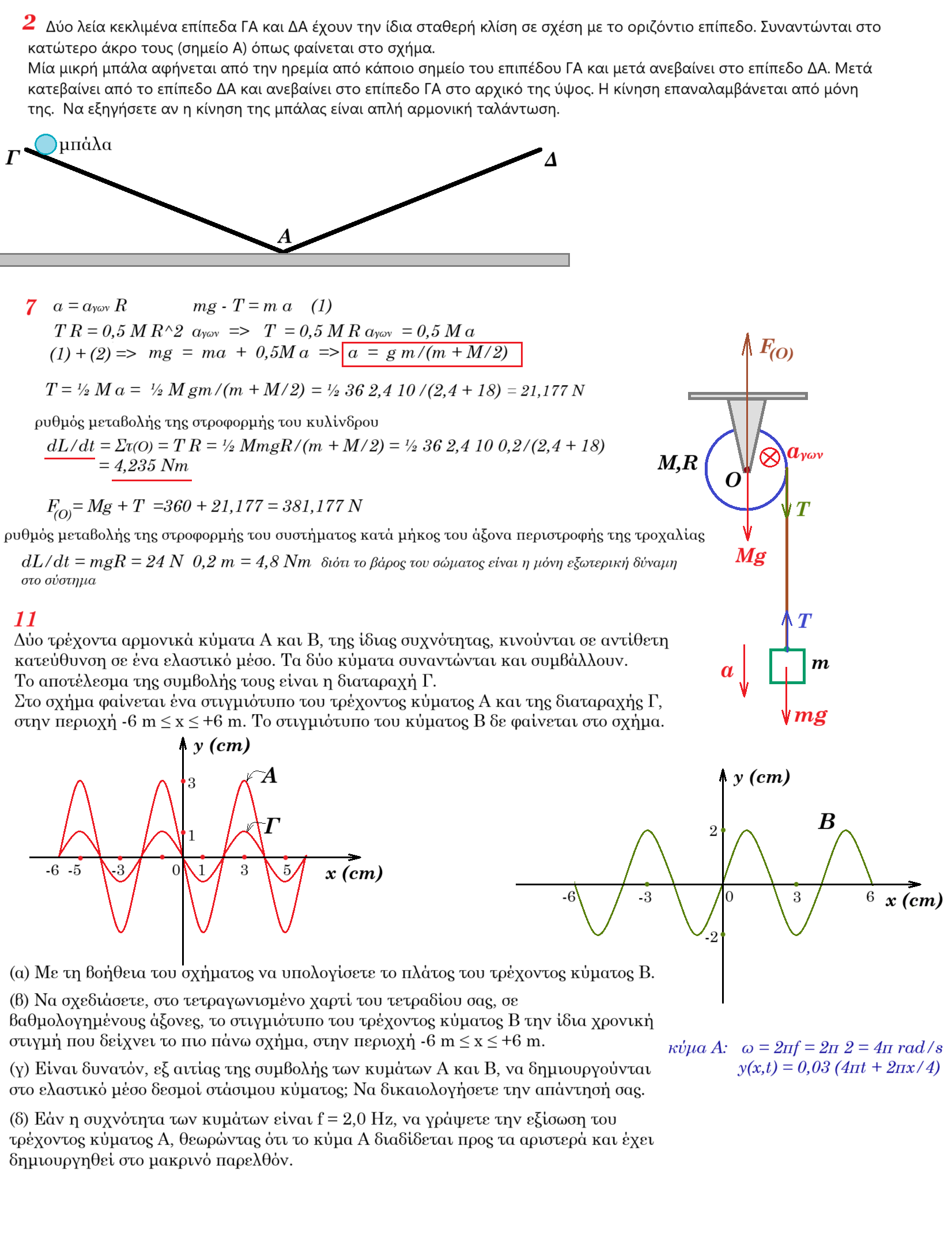
5. (α) Από κατακόρυφο ελατήριο σταθεράς k = 20 N/m κρέμεται σώμα μάζας 2 kg. Στο πάνω άκρο του ελατηρίου ασκείται εξωτερική περιοδική κατακόρυφη δύναμη που δίνεται από την εξίσωση F = 5 ημ (2π/3)t (S.I.).
Να υπολογίσετε την περίοδο ταλάντωσης του ταλαντωτή.
(β) Στις 19 Σεπτεμβρίου του 1985 έγινε σεισμός στη πόλη του Μεξικού. Πολλά κτήρια, ύψους 80 m περίπου, κατέρρευσαν, ενώ κτήρια ψηλότερα ή χαμηλότερα παρέμειναν άθικτα. Να χρησιμοποιήσετε τα παρακάτω στοιχεία για να εξηγήσετε τον λόγο για τον οποίο παρατηρήθηκε το φαινόμενο αυτό.

Η περίοδος ταλάντωσης ενός κτηρίου 80 m είναι 2,0 s. Η ταχύτητα διάδοσης των σεισμικών κυμάτων είναι 6,0×10³ m/s. Το μέσο μήκος κύματος των σεισμικών κυμάτων είναι 1,22×10⁴ m.

Α) ω_δ = 2π/3 rad/s f_δ = 2π / (2π/3) Hz = 3 Hz T_δ = 1/f_δ = 1/3 s

ο ταλαντωτής ταλαντώνεται με συχνότητα 3 Hz και περίοδο 1/3 s

k = m ω₀² => 20 = 2 ω₀² => ω₀ = √10 rad/s

η ιδιοσυχνότητα του ταλαντωτή είναι f₀ = 2π / √10 Hz = 2π/π Hz = 2 Hz

η ιδιοπερίοδος του ταλαντωτή είναι Τ₀ = 1/f₀ = 1/2 s

Β) λ = v T => T = 1,22×10⁴ m / 6,0×10³ m/s = 2,033... s περίοδος σεισμικών κυμάτων

η περίοδος ταλάντωσης των κτηρίων 80 m είναι 2 s άρα τα κτήρια συντονίστηκαν και κατέρευσαν

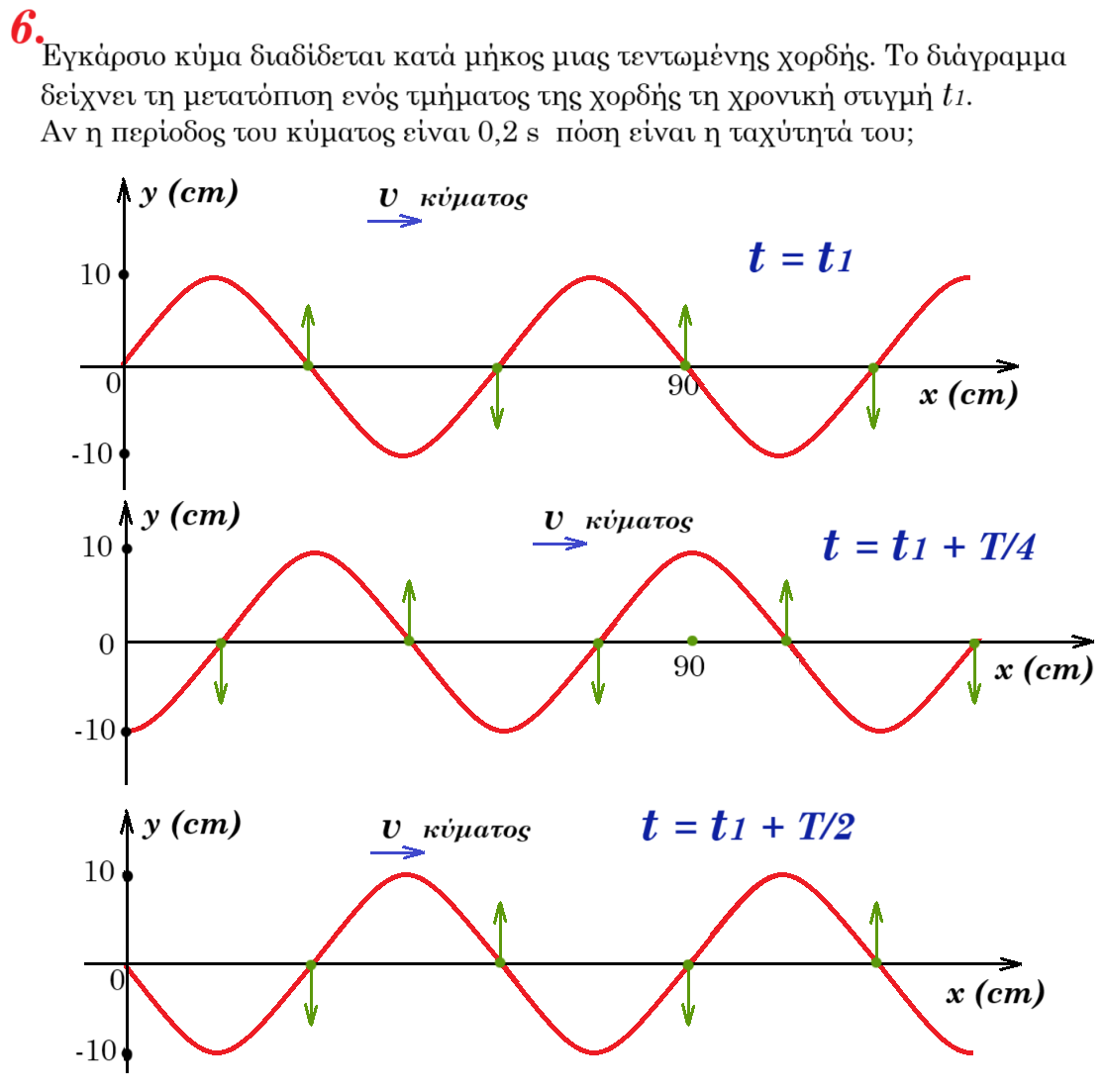
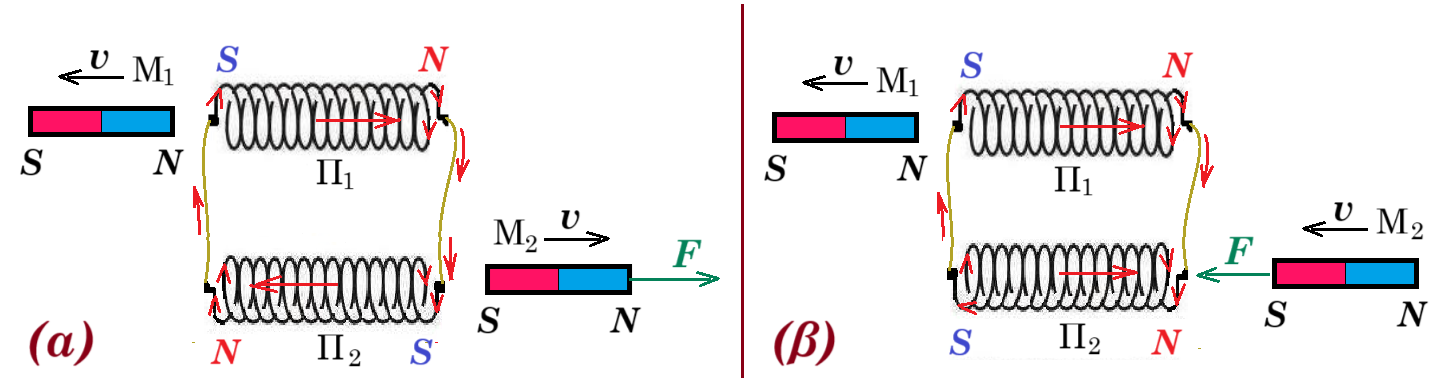
9. Στο πιο κάτω σχήμα φαίνονται δύο πηνία Π1 και Π2, τα οποία απέχουν αρκετά το ένα από το άλλο, και δύο ραβδόμορφοι μαγνήτες Μ1 και Μ2. Το μαγνητικό πεδίο του κάθε ραβδόμορφου μαγνήτη επηρεάζει μόνο το πηνίο που βρίσκεται δίπλα του.
Ο ραβδόμορφος μαγνήτης Μ1 απομακρύνεται από το πηνίο Π1, όπως φαίνεται στο πιο κάτω σχήμα. Το σχήμα δεν είναι σχεδιασμένο υπό κλίμακα.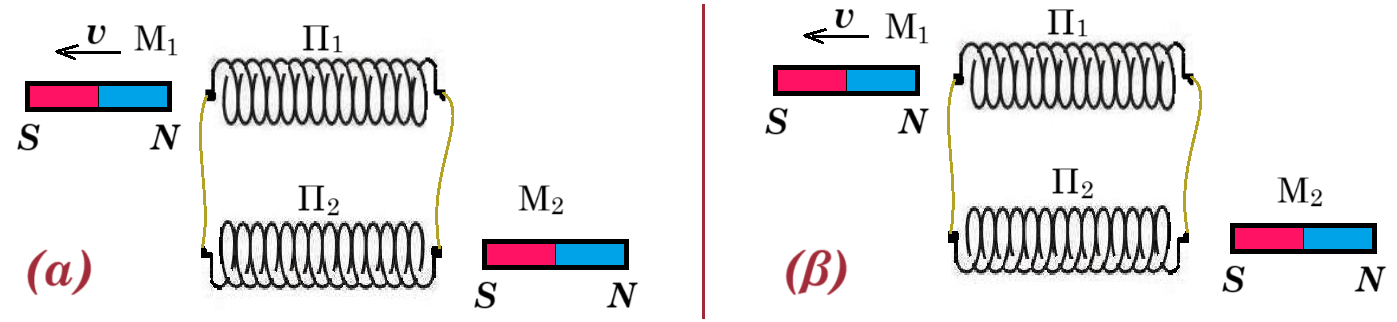

Να εξηγήσετε προς τα πού θα δεχθεί μαγνητική δύναμη ο μαγνήτης Μ2 που βρίσκεται ακίνητος δίπλα από το πηνίο Π2, καθώς ο μαγνήτης Μ1 απομακρύνεται από το πηνίο Π1 κατά μήκος του άξονα του πηνίου. (5 μονάδες)

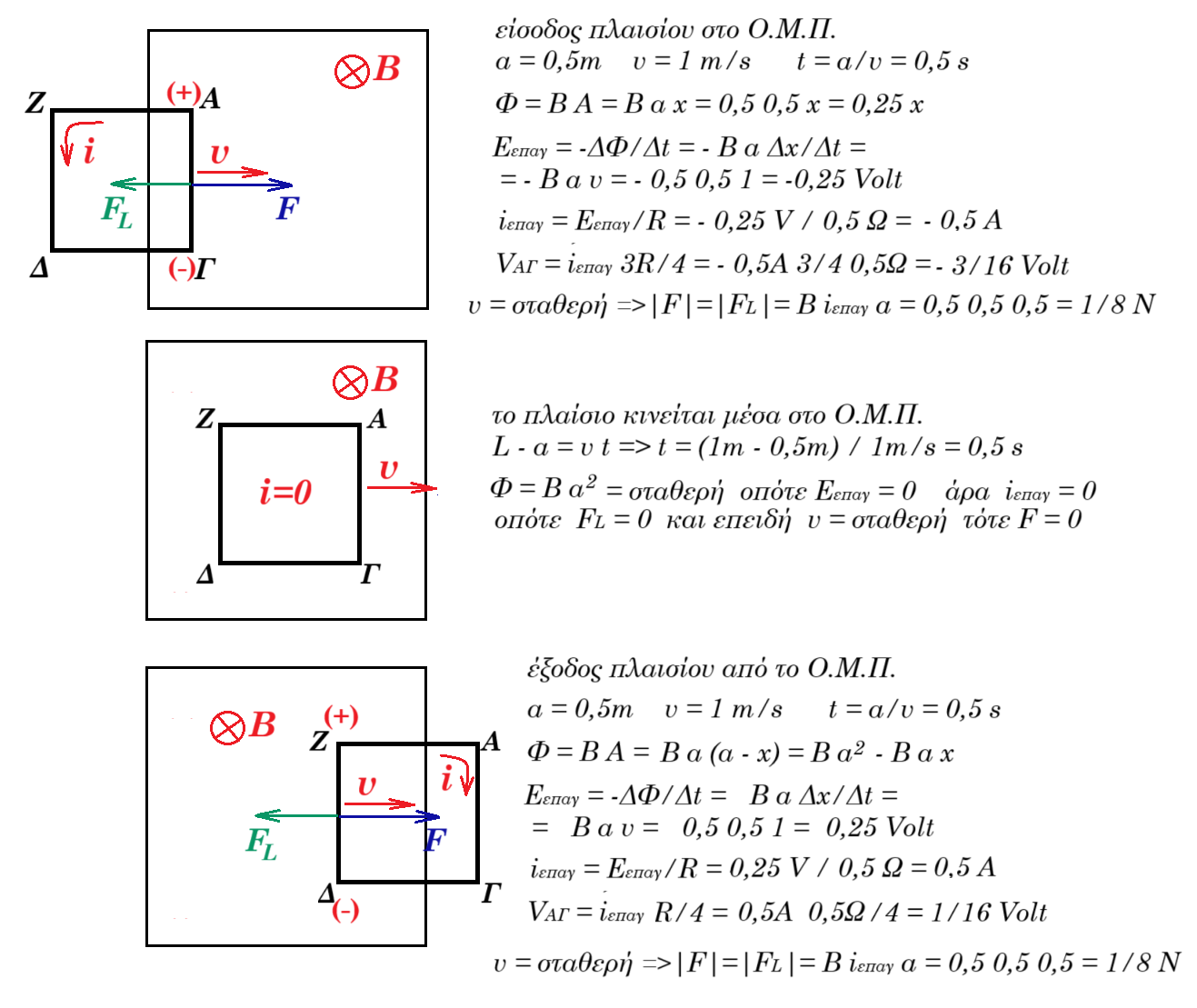
15. Τετράγωνο συρμάτινο πλαίσιο ΑΓΔΖ, πλευράς α = 0,5 m και συνολικής αντίστασης R = 0,5 Ω , είναι στερεωμένο κατακόρυφα σε πλαστικό αμαξάκι και εισέρχεται με σταθερή ταχύτητα, μέτρου υ = 1 m/s σε ομογενές μαγνητικό πεδίο έντασης μέτρου Β = 0,5 T, το οποίο είναι κάθετο στο επίπεδο του πλαισίου και στην ταχύτητα υ. Το πλαίσιο αρχίζει να εισέρχεται στο μαγνητικό πεδίο τη χρονική στιγμή t=0.

(α) Να εξηγήσετε γιατί θα πρέπει να ασκείται εξωτερική δύναμη στο πλαίσιο, παράλληλα προς την ταχύτητά του, έτσι ώστε το πλαίσιο να διατηρεί σταθερή ταχύτητα καθώς εισέρχεται στο μαγνητικό πεδίο.

(β) Να εξηγήσετε εάν θα πρέπει να ασκείται εξωτερική δύναμη στο πλαίσιο, παράλληλα προς την ταχύτητά του, έτσι ώστε αυτό να συνεχίσει να κινείται με σταθερή ταχύτητα, καθώς βρίσκεται ολόκληρο μέσα στο μαγνητικό πεδίο.

Ο χώρος που καταλαμβάνει το μαγνητικό πεδίο είναι κύβος ακμής L = 1 m.

(γ) Σχεδιάστε την δύναμη που πρέπει να ασκείται στο πλαίσιο ώστε να κινείται με σταθερή ταχύτητα, συναρτήσει του χρόνου, από τη στιγμή που εισέρχεται στο μαγνητικό πεδίο έως τη στιγμή που ολόκληρο εξέρχεται.

(δ) Σχεδιάστε την ηλεκτρεγερτική δύναμη από επαγωγή που δημιουργείται στο πλαίσιο, συναρτήσει του χρόνου, από τη στιγμή που εισέρχεται στο μαγνητικό πεδίο έως τη στιγμή που ολόκληρο εξέρχεται.

2016

5. Στο πιο κάτω διάγραμμα φαίνεται η γραφική παράσταση της ταχύτητας σε συνάρτηση με το χρόνο για ένα σώμα μάζας 2 kg, που εκτελεί γραμμική αρμονική ταλάντωση. Η δυναμική ενέργεια της ταλάντωσης τη χρονική στιγμή t = 0,1π s ισούται με 0,16 J.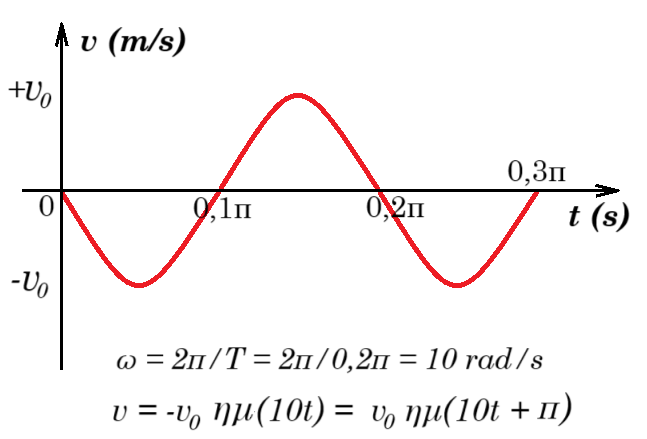

α) Βρείτε το πλάτος της ταλάντωσης και την επιτάχυνση του σώματος τη στιγμή t₁ = 0,25π s.

β) Εκφράστε τον ρυθμό μεταβολής της κινητικής ενέργειας του σώματος συναρτήσει του χρόνου.

v = - v₀ ημ(10t) = v₀ ημ(10t + π)

x = 0,1v₀ συν(10t) = - 0,1v₀ συν(10t + π)

α = - 10v₀ συν(10t) = 10v₀ συν(10t + π)

K = 0,5 m v₀² => 0,16 = 0,5 2 v₀² => v₀ = 0,4 m/s

U = 0,5 mω² Α² => 0,16 = 0,5 2 100 Α² => Α = 0,04 m

t = 0,05π s α = - 10v₀ συν(10 0,25π) = - 4 συν(2,5π) = 0

dK/dt = m v a = 2 ( - v₀ ημ(10t) ) ( - 10v₀ συν(10t) ) =

= 2 0,4 ημ(10t) 4 συν(10t) ) = 3,2 ημ(10t) συν(10t) = 1,6 ημ(20t)

6. Σώμα μάζας m = 400 g κρέμεται από το άκρο ενός ελατηρίου σταθεράς k = 40 N/m. Το σύστημα τίθεται σε εξαναγκασμένη ταλάντωση με την επίδραση εξωτερικής περιοδικής δύναμης συχνότητας 2/π Hz. Αν η συχνότητα της εξωτερικής δύναμης γίνει 4/π Hz, να εξηγήσετε πώς θα μεταβληθούν:
(i) Η συχνότητα της ταλάντωσης.
(ii) Το πλάτος της ταλάντωσης.

ιδιοσυχνότητα ταλάντωσης σώματος :

ω₀ = √(k/m) = √(40/0,4) => ω₀ = 10 rad/s f₀ = 10/2π = 5/π Hz

2/π Hz < 4/π Hz < 5/π Hz οπότε το σώμα ταλαντώνεται με συχνότητα 4/π Hz και το πλάτος της ταλάντωσής του αυξάνεται

14. Δύο σύγχρονες πηγές Π1 και Π2 αρχίζουν να δημιουργούν εγκάρσια κύματα στην επιφάνεια του νερού τη χρονική στιγμή t = 0 s.
Η εξίσωση της ταλάντωσης της κάθε πηγής δίνεται από τη σχέση y = 2ημ(5πt) όπου y σε cm και t σε s. Ένα σημείο Σ της επιφάνειας του νερού απέχει απόσταση r₁= 4 m από την πηγή Π1 και απόσταση r₂από την πηγή Π2, με r₂> r₁.
Το κύμα από την πηγή Π1 φτάνει στο σημείο Σ τη χρονική στιγμή t₁= 0,4 s και από την πηγή Π2 με καθυστέρηση Δt = 0,4 s.
(α) Να βρείτε την ταχύτητα διάδοσης και το μήκος κύματος των κυμάτων. (Μονάδες 3)
(β) Να υπολογίσετε την απόσταση r₂. (Μονάδες 2)
(γ) Να διερευνήσετε πώς συμβάλουν τα κύματα στο σημείο Σ. (Μονάδες 2)
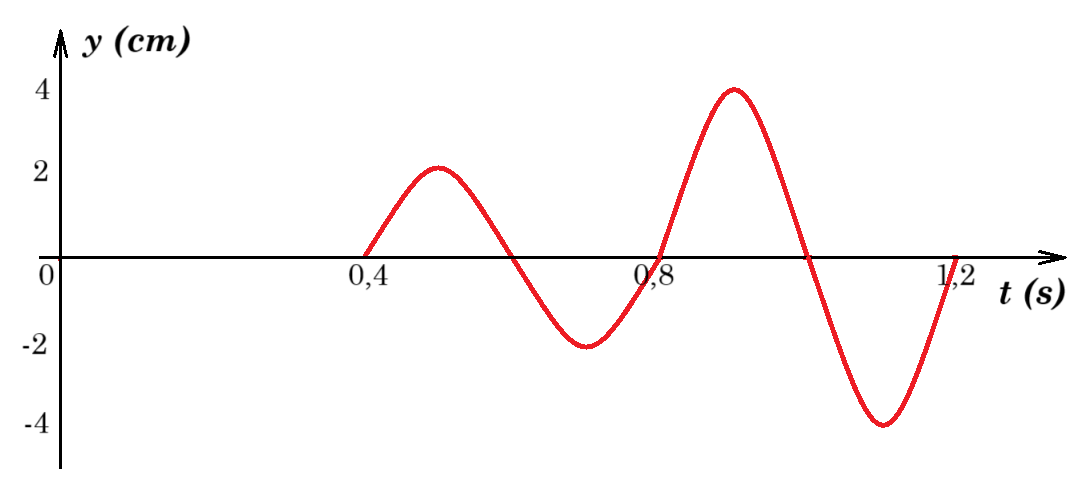
(δ) Nα σχεδιάσετε σε βαθμολογημένους άξονες τη γραφική παράσταση της μετατόπισης του σημείου Σ σε συνάρτηση με το χρόνο, y = f(t), για 0s  t  1,2s. (Μονάδες 2)
Να θεωρήσετε ότι το πλάτος των επιφανειακών κυμάτων παραμένει σταθερό κατά τη διάδοσή τους στο νερό.

r₁ = v t₁ => 4m = v 0,4s => v = 10 m/s ταχύτητα διάδοσης κύματος

ω = 5π rad/s => Τ = 2π/ω = 2/5 = 0,4 s λ = υ Τ = 10 0,4 = 4 m Δt = 0,4 s = T

στο σημείο Σ το δεύτερο κύμα φθάνει σε χρόνο 0,4 + 0,4 = 0,8 s r₂ = v t₂ = 10 m/s 0,8 s = 8 m

Δr = r₂ - r₁ = 8m - 4m = 4m = 10 λ τα δύο κύματα συμβάλουν ενισχυτικά

1,2 s = 3 0,4 s = 3 T

2012

12. Σε ένα τεντωμένο μακρύ ελατήριο διαδίδεται ένα τρέχον κύμα του οποίου το πλάτος είναι 6,0 cm. Η περίοδος ταλάντωσης της πηγής η οποία παράγει το κύμα είναι 0,40 s. Το κύμα διαδίδεται σε απόσταση 2 m σε χρόνο 0,80 s.
(α) Να υπολογίσετε:
(i) τη συχνότητα του κύματος (Μονάδα 1)
(ii) την ταχύτητα διάδοσης του κύματος. (Μονάδα 2)
(β) Να γράψετε την εξίσωση του κύματος. (Μονάδες 2)
(γ) Να υπολογίσετε:
(i) τη μετατόπιση του μορίου μιας σπείρας του ελατηρίου το οποίο βρίσκεται σε απόσταση 2,30 m από την πηγή 5,0 s μετά την έναρξη ταλάντωσης της πηγής (Μονάδες 2)
(ii) τη μέγιστη ταχύτητα ταλάντωσης των μορίων του ελατηρίου. (Μονάδες 2)
(δ) Η ταχύτητα διάδοσης του κύματος αυξάνει με την επιμήκυνση του ελατηρίου. Το ελατήριο επιμηκύνεται έτσι ώστε η ταχύτητα διάδοσης της διαταραχής να γίνει διπλάσια της αρχικής, ενώ η συχνότητα παραμένει σταθερή. Να αναφέρετε το νέο μήκος κύματος της διαταραχής. (Μονάδες 1)

f = 1/T = 1 / 0,4s = 2,5 Hz ω = 2π/Τ = 2π / 0,4 = 5π rad/s v = 2m / 0,8s = 2,5 m/s

λ = v T = 2,5 m/s 0,4 s = 1 m

y(x,t) = 0,06 ημ(5πt - 2πx/1) v(x,t) = 0,3π συν(5πt - 2πx)

y(2,3m , t=5s) = 0,06 ημ(5π 5 - 2π 2,3/1) = 0,06 ημ(25π - 4,6π) = 0,06 ημ(20,4π) = 0,06 0,951 m = 0,057 m

εφ'όσον διπλασιάζεται η ταχύτητα ενώ η συχνότητα μένει η ίδια το μήκος κύματος διπλασιάζεται

2011

14. Α. Μια οµάδα παιδιών συναρµολόγησαν τη διάταξη του σχήµατος για τη δηµιουργία στάσιµων κυµάτων. Η σταθερή συχνότητα του διεγέρτη είναι f = 25 Hz. Επέλεξαν το µήκος της χορδής ΚΛ : (ΚΛ) = L= 0,8 m, και τοποθετώντας σταθµά, κατάλληλης µάζας, πέτυχαν να δηµιουργήσουν στη χορδή στάσιµο κύµα µε δύο κοιλίες.

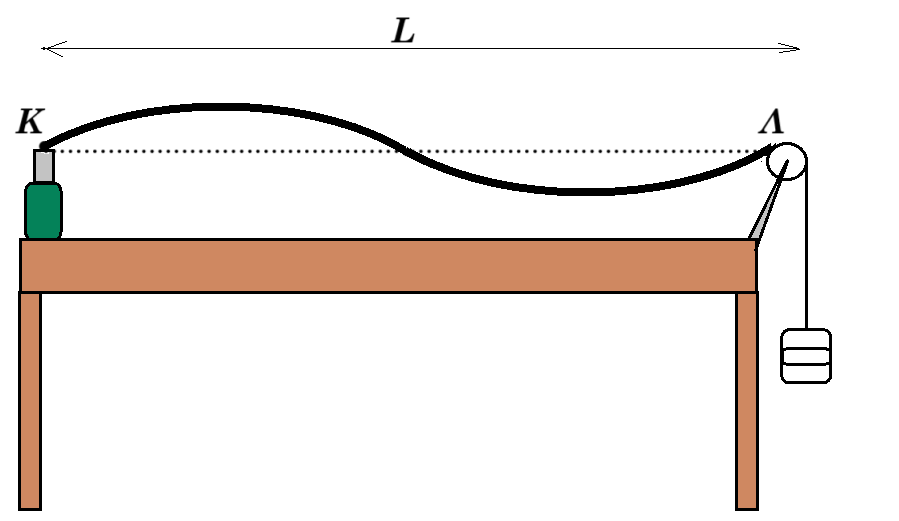
Για το τρέχον κύµα που δηµιουργεί ο διεγέρτης να υπολογίσετε:
(α) Το µήκος κύµατός του. (Μονάδα 1)
(β) Την ταχύτητα διάδοσής του στη χορδή. (Μονάδα 1)

Β. Θεωρούµε ότι το στιγµιότυπο του πιο κάτω στάσιµου κύµατος, συχνότητας f = 25 Ηz, αντιστοιχεί στη χρονική στιγµή t0 = 0, κατά την οποία όλα τα σηµεία της χορδής έχουν ταχύτητα µηδέν.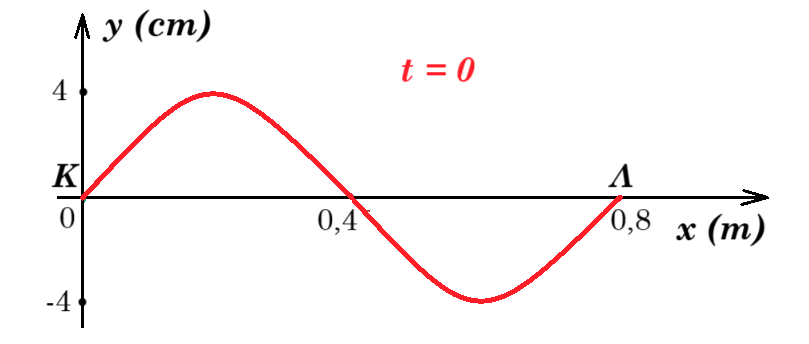

(α) Να σχεδιάσετε το στιγµιότυπο του στάσιµου κύµατος για τις χρονικές στιγµές t1 = T/4 και t2 = Τ/2 σε δύο διαφορετικά σχήµατα, όπου Τ η περίοδος του κύµατος. (Μονάδες 2)
(β) Να υπολογίσετε την ταχύτητα ταλάντωσης του σηµείου Α (x_A=0,1m) για τη χρονική στιγµή t1. (Μονάδες 2)
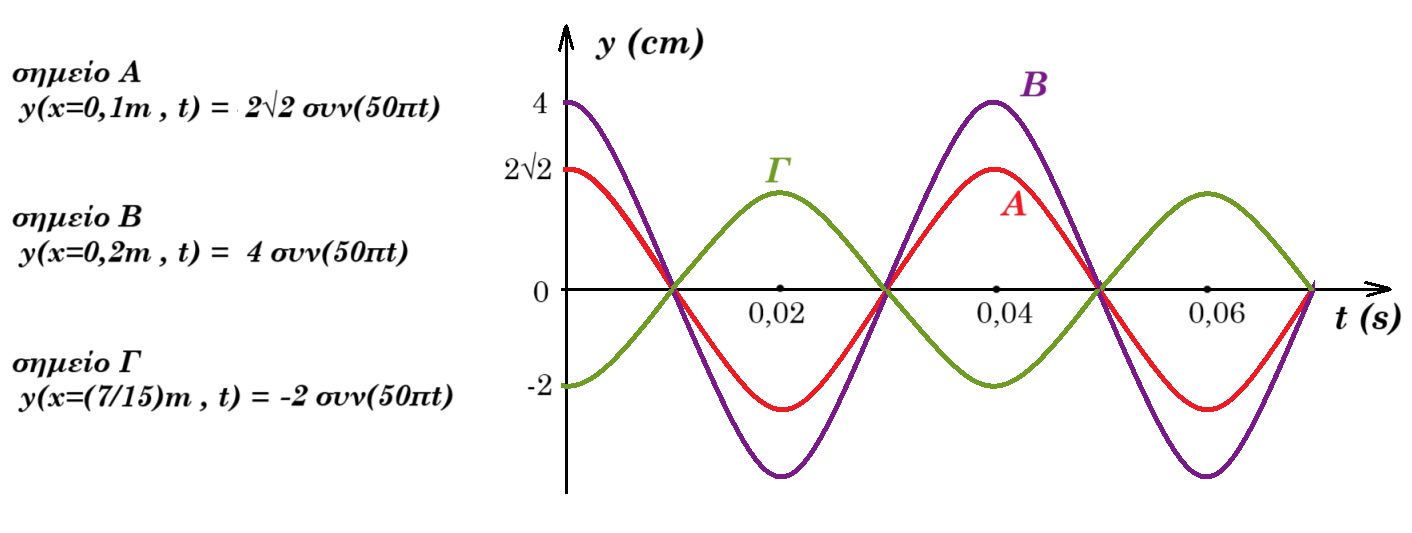
(γ) Να σχεδιάσετε τις γραφικές παραστάσεις της αποµάκρυνσης y από τη θέση ισορροπίας τους, σε συνάρτηση µε το χρόνο t, y = f(t), για τα σηµεία Α (x_A=0,1m) , Β (x_B=0,2m) και Γ (x_Γ=7/15m) της χορδής, στους ίδιους βαθµολογηµένους άξονες. (Μονάδες 4)

(Α) λ = L = 0,8 m T = 1/f = 1/25 = 0,04 s v = λ f = 0,8 m 25 Hz = 20 m/s

(B) (α) t₁ = T/4 = 0,01 s t₂ = T/2 = 0,02 s

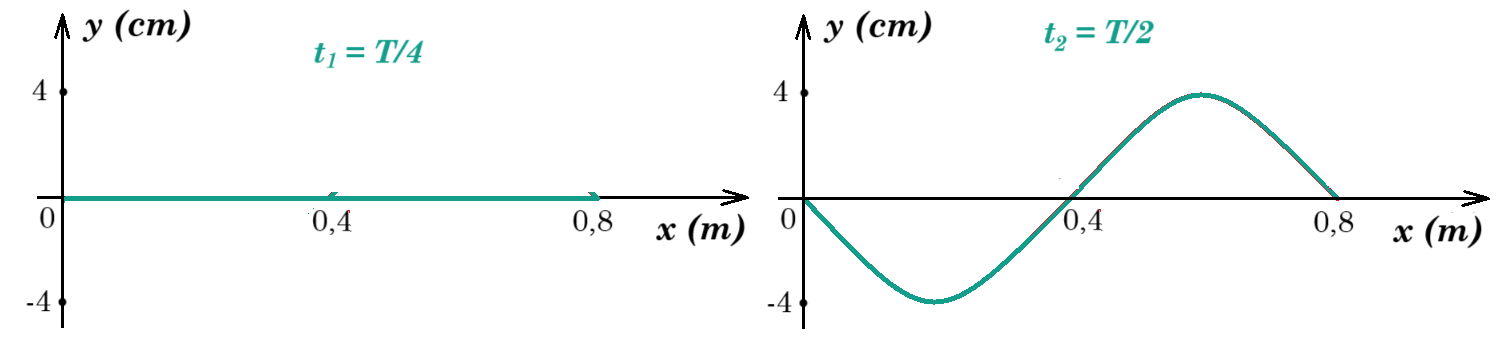
μελέτη της συνάρτησης y(x)

τα σημεία της χορδής έχουν ταχύτητα μηδέν άρα είναι στην μέγιστη απομάκρυνσή τους τη στιγμή μηδέν

επειδή η θέση x=0 είναι δεσμός και επειδή τη στιγμή t=0 τα σημεία της χορδής βρίσκονται στη μέγιστη απομάκρυνσή τους έχοντας ταχύτητα μηδέν η εξίσωση του στασίμου κύματος θα είναι :

y(x,t) = 4 ημ(2πx/0,8) συν(2πt/0,04) όπου y σε cm , t σε sec

y(x=0,1 , t=0) = 4 ημ(2π 0,1/0,8) συν(2π 0/0,04) = 4 ημ(π/4) συν(0) = 2√2 cm

y(x=0,2 , t=0) = 4 ημ(2π 0,2/0,8) συν(2π 0/0,04) = 4 ημ(π/2) συν(0) = 4 cm

y(x=0,3 , t=0) = 4 ημ(2π 0,3/0,8) συν(2π 0/0,04) = 4 ημ(3π/4) συν(0) = 2√2 cm

y(x=0,4 , t=0) = 4 ημ(2π 0,4/0,8) συν(2π 0/0,04) = 4 ημ(π) συν(0) = 0 cm

y(x=0,5 , t=0) = 4 ημ(2π 0,5/0,8) συν(2π 0/0,04) = 4 ημ(5π/4) συν(0) = - 2√2 cm

y(x=0,6 , t=0) = 4 ημ(2π 0,6/0,8) συν(2π 0/0,04) = 4 ημ(3π/2) συν(0) = - 4 cm

y(x=0,7 , t=0) = 4 ημ(2π 0,7/0,8) συν(2π 0/0,04) = 4 ημ(7/4) συν(0) = - 2√2 cm

y(x=0,8 , t=0) = 4 ημ(2π 0,8/0,8) συν(2π 0/0,04) = 4 ημ(2π) συν(0) = 0 cm

*******

(B) (β)

y(x=0,1 , t=0,01) = 4 ημ(2π 0,1/0,8) συν(2π 0,01/0,04) = 4 ημ(π/4) συν(π/2) = 0 cm

y(x=0,1 , t=0,02) = 4 ημ(2π 0,1/0,8) συν(2π 0,02/0,04) = 4 ημ(π/4) συν(π) = - 2√2 cm

y(x,t) = 4 ημ(2π x/0,8) συν(2π t/0,04) = 4 ημ(2,5π x) συν(50π t) εξίσωση στάσιμου

v(x,t) = 4 50π ημ(2π x/0,8) [- ημ(50π t) ] = - 200π ημ(2π x/0,8) ημ(50π t) εξίσωση ταχύτητας των σημείων της χορδής

v(x=0,1m , t=0,01s) = - 200π ημ(2π 0,1/0,8) ημ(50π 0,01) =

= - 200π ημ(π/4) ημ(π/2) = - 200π √2/2 1 = - 100π√2 cm/s = - π√2 m/s

η ταχύτητα του σημείου Α (x_A=0,1m) τη στιγμή t=T/4 = 0,01s

*******

εάν επιλέξουμε

τότε το άκρο Κ της χορδής ΚΛ βρίσκεται στη θέση x_Κ = -0,2m το άκρο Λ βρίσκεται στη θέση x_Λ = +0,6m το σημείο Ρ στη θέση x_Ρ = 0 είναι κοιλία οπότε η εξίσωση του στάσιμου κύματος είναι :

y(x,t) = 4 συν(2πx/0,8) συν(2πt/0,04) όπου y σε cm , t σε sec

y(x=-0,2 , t=0) = 4 συν(- 2π 0,2/0,8) συν(2π 0/0,04) = 4 συν(- π/2) συν(0) = 0 cm

y(x=-0,1 , t=0) = 4 συν(- 2π 0,1/0,8) συν(2π 0/0,04) = 4 συν(- π/4) συν(0) = 2√2 cm

y(x=0 , t=0) = 4 συν(2π 0/0,8) συν(2π 0/0,04) = 4 συν(0) συν(0) = 4 cm

y(x=0,1 , t=0) = 4 συν(2π 0,1/0,8) συν(2π 0/0,04) = 4 συν(π/4) συν(0) = 2√2 cm

y(x=0,2 , t=0) = 4 συν(2π 0,2/0,8) συν(2π 0/0,04) = 4 συν(π/2) συν(0) = 0 cm

y(x=0,3 , t=0) = 4 συν(2π 0,3/0,8) συν(2π 0/0,04) = 4 συν(3π/4) συν(0) = - 2√2 cm

y(x=0,4 , t=0) = 4 συν(2π 0,4/0,8) συν(2π 0/0,04) = 4 συν(π) συν(0) = - 4 cm

y(x=0,5 , t=0) = 4 συν(2π 0,5/0,8) συν(2π 0/0,04) = 4 συν(5π/4) συν(0) = - 2√2 cm

y(x=0,6 , t=0) = 4 συν(2π 0,6/0,8) συν(2π 0/0,04) = 4 συν(3π/2) συν(0) = 0 cm

(Β) (γ) y(x,t) = 4 ημ(2πx/0,8) συν(2πt/0,04) όπου y σε cm , t σε sec

σημείο Α y(x=0,1m , t) = 4 ημ(2π 0,1/0,8) συν(2πt/0,04) = 4 ημ(π/4) συν(50πt) = 2√2 συν(50πt)

σημείο Β y(x=0,2m , t) = 4 ημ(2π 0,2/0,8) συν(2πt/0,04) = 4 ημ(π/2) συν(50πt) = 4 συν(50πt)

y(x,t) = 4 ημ(2πx/0,8) = -2 => ημ(2πx/0,8) = -0,5 => ημ(2,5πx) = ημ(7π/6) =>

2,5πx = 7π/6 => x = 7/15 m

σημείο Γ y(x=(7/15)m , t) = 4 ημ(2π (7/15)/0,8) συν(2πt/0,04) = 4 ημ(7π/6) συν(50πt) = -2 συν(50πt)

2007

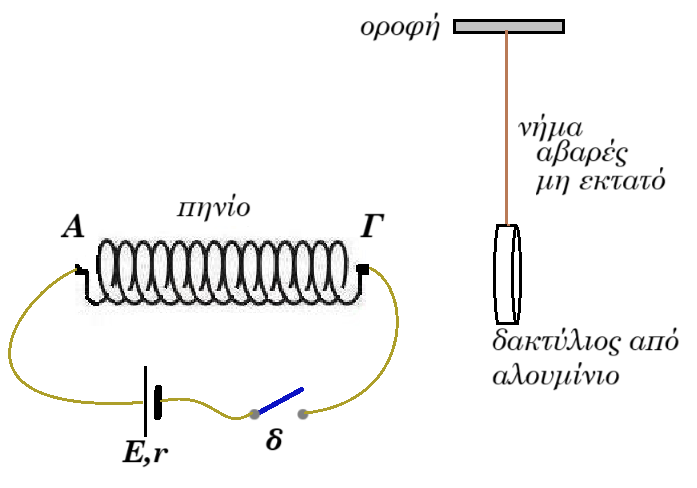4. (α) Να διατυπώσετε τον κανόνα του Lenz. (μονάδες 2 )
(β) Ποιος βασικός νόμος της Φυσικής θα παραβιαζόταν αν δεν ίσχυε ο κανόνας του Lenz; (μονάδα 1)
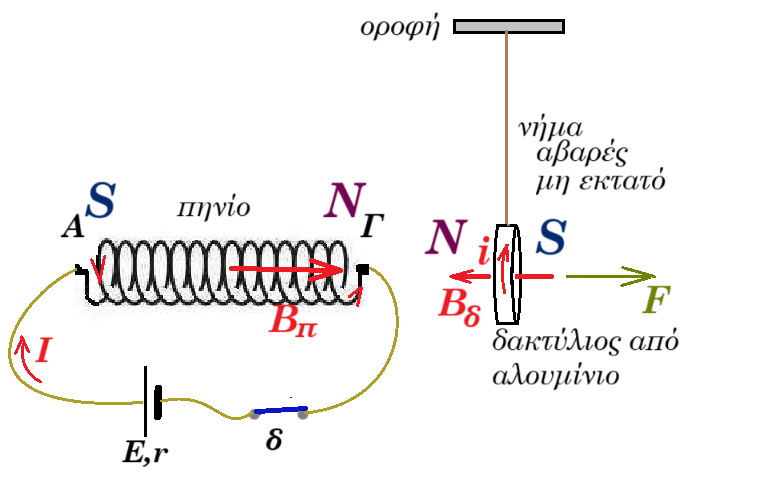
(γ) Στο πιο πάνω σχήμα, κατά το κλείσιμο του διακόπτη δ, ο δακτύλιος μετακινείται προς τα δεξιά. Να εξηγήσετε την παρατήρηση αυτή. (μονάδες 2 )

(β) παραβιάζεται η διατήρηση της ενέργειας

(γ) όταν κλείσουμε τον διακόπτη δ το πηνίο διαρρέεται από ρεύμα με συνέπεια την εμφάνιση μαγνητικού πεδίου στο πηνίο με τον βόρειο πόλο στο άκρο του Γ και τον νότιο πόλο στο άκρο του Α

τότε αυξάνεται η μαγνητική ροή που διέρχεται μέσα από τον δακτύλιο με συνέπεια να κυκλοφορήσει επαγωγικό ρεύμα στο εσωτερικό του δακτυλίου που με τη σειρά του δημειουργεί μαγνητικό πεδίο με τον βόρειο πόλο προς τη μεριά του πηνίου

έτσι ο δακτύλιος απωθείται από το πηνίο