1η  περίπτωση                             

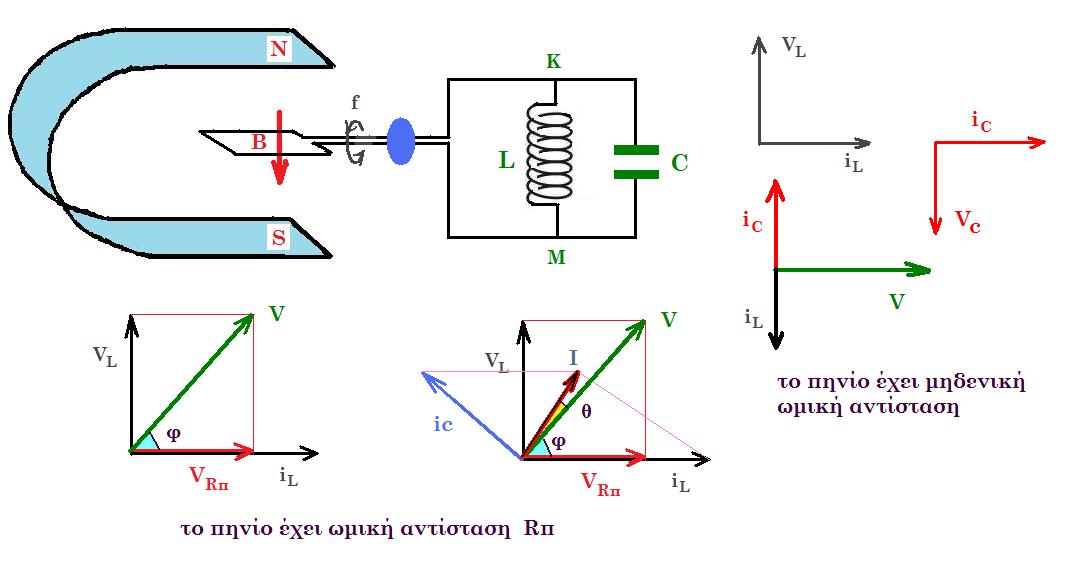
                             το πηνίο έχει μηδενική ωμική αντίσταση

V₀ . ημωt  - L . di_L / dt  = 0   =>   V₀ . ημωt  =  L . di_L / dt   => V₀ / L . ημωt  =  di_L / dt   =>    i_L(t)  = - V₀ / Lω . συνωt  = V₀ / Lω . ημ(ωt - π/2)    για το πηνίο

V₀ . ημωt = V_C = q / C   =>  1/C . dq / dt  =  ω.V₀ .  συνωt    =>  i_C = dq / dt  =  C.ω.V₀ . συνωt  = C.ω.V₀ . ημ(ωt + π/2)      για τον πυκνωτή

το συνολικό ρεύμα :  i  =  i_L  +  i_C   =   - V₀ / Lω . συνωt  +  C.ω.V₀ . συνωt  =    V₀ . [ C.ω - (1 / Lω) ] . συνωt   

         το πλάτος της έντασης ρεύματος :  Ι  =   V₀ . [ C.ω - (1 / Lω) ] 

 η εμπέδηση  Ζ  του κυκλώματος :  1 / Ζ  =   C.ω - (1 / Lω)  =   1 / Ζ_C  -  1 /  Ζ_L

------------------------------------------------------------------------------------------------------------------------------

                                                    2η  περίπτωση                    

                                  το πηνίο έχει ωμική αντίσταση R_π

            V₀ . ημωt  =   L . di_π / dt  +  i_π . R_π   (1)            i_π (t) =   Α . ημ(ωt + φ) = Α . ( ημωt . συνφ  +  συνωt . ημφ )      για το πηνίο  

   di_π / dt  =   Α . ω . ( συνωt . συνφ  -  ημωt . ημφ )         η  (1) =>     V₀ . ημωt  =    Α . ω . ( συνωt . συνφ  -  ημωt . ημφ )  +  Α . ( ημωt . συνφ  +  συνωt . ημφ )  . R_π  

εξισώνουμε τους συντελεστές ως προς   τα   συνωt  :    0     =    Α . ωL .  συνφ   +  Α .  ημφ . R_π    =>    ωL .  συνφ   =  - ημφ . R_π   =>  - ωL / Rπ   =    εφφ    

από τις σχέσεις     εφφ = ημφ / συνφ     και     ημ² φ + συν² φ = 1    έχουμε :       εφ² φ + 1 = 1 / συν² φ   (4)   και     1/εφ² φ + 1 = 1 / ημ² φ   (5)

η (4) => 1 / συν² φ = ( - ωL / R_π )² + 1 =>   συν² φ = R_π ² / [ (ωL)² + R_π² ]     =>      συνφ = R_π / [ (ωL)² + R_π² ]^½    =>   συνφ = R_π / Ζ_π      όπου   Ζ_π = [ (ωL)² + R_π² ]^½ 

η (5) => 1 / ημ² φ = ( - R_π / ωL )² + 1   =>    ημφ = - (ωL) / [ (ωL)² + R_π² ]^½     =>   ημφ = - ωL / Ζ_π      όπου   Ζ_π = [ (ωL)² + R_π )² ]^½   

εξισώνουμε τους συντελεστές ως προς   τα    ημωt  :   V₀  = - Α . ωL .  ημφ   +  Α . συνφ  . R_π   =>   V₀  =  - Α . ωL .( - ωL / Ζ_π  )  +  Α .( R_π / Ζ_π ) . R_π   =>

     =>  V₀  =  Α . (ωL)² / Ζ_π +  Α . Rπ² / Ζ_π       =>  V₀  =  Α . [ (ωL)²  +  Rπ² ] / Ζ_π   =>     V₀  =  Α . Ζ_π² / Ζ_π    =>    Α = V₀ / Ζ_π  = Ι_0,πην     πλάτος ρεύματος που διαρρέει το πηνίο

                               άρα   i_π (t) =   Α . ημ(ωt + φ)      =>          i_π (t) = V₀ / Ζ_π . ημ(ωt + φ)  ,  εφφ = - ωL / Rπ ,  Ζ_π = [ (ωL)² + R_π )² ]^½ 

V₀ . ημωt = V_C = q / C   =>  1/C . dq / dt  =  ω.V₀ .  συνωt    =>  i_C = dq / dt  =  C.ω.V₀ . συνωt  = C.ω.V₀ . ημ(ωt + π/2)      για τον πυκνωτή

το ολικό ρεύμα :   i   =  i_π  +   i_C   =    V₀ / Ζ_π . ημ(ωt + φ)   +   C.ω.V₀ . συνωt   =  

                                      =   V₀ / Ζ_π . ( ημωt . συνφ  +  συνωt . ημφ ) + C.ω.V₀ . συνωt  =   Ι . ημ(ωt + θ)  =  Ι . ( ημωt . συνθ  +  συνωt . ημθ )   

εξισώνουμε τους συντελεστές ως προς   τα    ημωt  : V₀ / Ζ_π . συνφ  = Ι . συνθ    (6)

εξισώνουμε τους συντελεστές ως προς   τα   συνωt  : V₀ / Ζ_π . ημφ  + C.ω.V₀  =   Ι . ημθ   (7)

(7) : (6)  =>  εφθ  =   ( V₀ / Ζ_π . ημφ  + C.ω.V₀  )  /  (  V₀ / Ζ_π . συνφ  )   =    ( V₀ / Ζ_π . - ωL / Ζ_π + C.ω.V₀  )  /  (  V₀ / Ζ_π . R_π / Ζ_π )   =

                              =   ( - ωL/ Ζ_π ²  +  C.ω )  /  (  Rπ  / Ζ_π ²)   =    ( - ωL +   Ζ_π ² . C.ω )  /   Rπ   

     εφθ  =  ( - ωL + [ (ωL)² + R_π )² ] . C.ω )  / Rπ     =>    εφθ  =  { - ωL + [ (ωL)² + R_π )² ] . C.ω }  /   R_π 

(6) ²  +  (7) ²  =>   Ι²  = ( V₀ / Ζ_π . ημφ  + C.ω.V₀  )²  +  (  V₀ / Ζ_π . συνφ  )²    =>     Ι₀²  =   V₀ ² . {   ( - ωL/ Ζ_π ²  +  C.ω )²  +  (  Rπ  / Ζ_π ²)²     }       =>   Ι₀²  =   V₀ ² .  1/Ζ²  

        η εμπέδηση  Ζ   του κυκλώματος  :     1 / Ζ²  =   {   ( - ωL/ Ζ_π²  +  C.ω )²  +  (  Rπ  / Ζ_π² )²   }