1η περίπτωση                     

                                        το πηνίο έχει μηδενική ωμική αντίσταση

i = dq/dt    --->    di/dt = d²q/d²t  

V_ΚΜ  =  V₀ . ημωt  =  L . di/dt  +  q/C  =>   V₀ . ημωt  =  L . d²q/d²t +  q/C    (1)

q = Q . ημ(ωt + φ)   =>   dq/dt =  ω.Q . συν(ωt + φ)   =>   d²q/d²t = - ω² .Q . ημ(ωt + φ)

(1) =>   V₀ . ημωt  =  - ω² .L .Q . ημ(ωt + φ)  +   Q/C . ημ(ωt + φ)   => 

      =>  V₀ . ημωt  =  ω.Q. ( 1/ωC  - ω.L ). ημ(ωt + φ)

      =>  V₀ . ημωt  =   ω.Q. ( 1/ωC  - ω.L ). ( ημωt . συνφ  +  συνωt . ημφ )   

   εξισώνουμε τα συνωt :    0  =  ω.Q. ( 1/ωC  - ω.L ).    ημφ  =>  ημφ  =  0   άρα   συνφ  =  1 

   εξισώνουμε τα ημωt :     V0  =  ω.Q. ( 1/ωC  - ω.L ).  συνφ  =>  V0 =  ω.Q. ( 1/ωC  - ω.L )  =>

      =>   Q  =  V0  / ω.( 1/ωC  - ω.L )   τότε  q = Q . ημ(ωt + φ)  =>   V0 / ω.( 1/ωC - ω.L ) . ημωt  =  q(t)      το φορτίο του πυκνωτή συναρτήσει του χρόνου 

          Ζ = 1/ωC  - ω.L  :   εμπέδηση κυκλώματος 

το ρεύμα που διαρρέει το κύκλωμα :   i  =  dq/dt  =   ω.Q . συν(ωt + φ)  =>

 =>  i(t)  =  V0  / ( 1/ωC  - ω.L ) . συνωt   =   V0  / (ω.L  -  1/ωC ) . ημ(π/2 - ωt)    

 υπάρχει περίπτωση    1/ωC  - ω.L ® 0  =>  ω² .L. C  ® 1  =>   ω  ®  1 / (L. C)^½  = ω₀  ιδιοσυχνότητα του κυκλώματος      τότε  το φορτίο  στον πυκνωτή   γίνεται  άπειρο  όπως και το ρεύμα που διαρρέει το πηνίο  

................................................................................................................................................................

                                                      2η περίπτωση                  

                                   το πηνίο έχει ωμική αντίσταση  R

i = dq/dt             i =  I . ημ(ωt + φ)   ®   q =  - I/ω . συν(ωt + φ)      ®    di/dt = I.ω . συν(ωt + φ)

       V_ΚΜ  =  V₀ . ημωt  =  L . di/dt  +  q/C  +  i . R      =>  

  =>   V₀ . ημωt  =   L . I.ω . συν(ωt + φ)   -   I/ωC . συν(ωt + φ)  +  I . ημ(ωt + φ) . R   =>

  =>   V₀ . ημωt  =   I. ( ωL  -  1/ωC ) . συν(ωt + φ)  +  I .R. ημ(ωt + φ)      

  =>   V0 . ημωt  =   I. ( ωL  -  1/ωC ) . ( συνωt . συνφ - ημωt . ημφ ) +  I .R.( ημωt . συνφ + συνωt . ημφ )

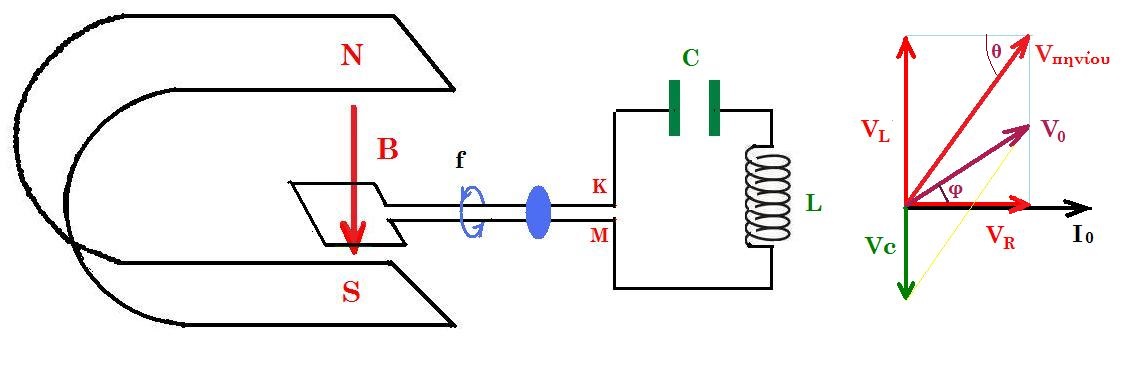
 εξισώνουμε τα συνωt :      I. ( ωL  -  1/ωC ) .  συνφ   +  I .R.  ημφ  =  0    =>        εφφ  =  - ( ωL - 1/ωC ) / R ,

     ημφ =  - ( ωL - 1/ωC ) / Ζ ,    συνφ  =  R / Ζ  ,       Ζ²  =  ( ωL - 1/ωC )²  + R ²

 εξισώνουμε τα ημωt :       V₀  = - I. ( ωL - 1/ωC ) . ημφ  +  I .R . συνφ   =>

    =>  V₀  =  I. ( ωL - 1/ωC ) . ( ωL - 1/ωC ) / Ζ +  I .R .R / Ζ   => 

    =>  V₀  =  I. ( ωL - 1/ωC )²   / Ζ +  I .R²  / Ζ   =>    V₀  =  I. Ζ² / Ζ   =>   V₀  =  I. Ζ   =>    I  =  V0  /  Ζ      μέγιστη ένταση ρεύματος        i(t) =  I . ημ(ωt + φ) = V₀ / Ζ . ημ(ωt + φ)

το φορτίο του πυκνωτή :      q  =  - I/ω . συν(ωt + φ)   =>      q  =  - (V₀ / Ζ.ω) . συν(ωt + φ)       

   V_C  =  q / C  = - ( V₀ / ω.Ζ ) / C . συν(ωt + φ)   =   - ( V₀ / ω.C. Ζ ) . συν(ωt + φ)    η τάση στα άκρα του πυκνωτή

   V_L  =   L . di/dt  =  L . I . ω . συν(ωt + φ)   =     V0 .(ωL / Ζ) . συν(ωt + φ)   η τάση αυτεπαγωγής του πηνίου

   V_R  =  i . R  =    V₀ . (R / Ζ) . ημ(ωt + φ)      η πτώση τάσης στην ωμική αντίσταση του πηνίου

   V_πηνίου   =   V_L  + V_R  =    V₀ .(ωL / Ζ) . συν(ωt + φ)  +  V₀ . (R / Ζ) . ημ(ωt + φ)  =>  

  =>   V_πηνίου   =  V_0,πην  . ημ(ωt + φ + θ)   =   V_0,πην  .[ ημ(ωt + φ) . συνθ  +   συν(ωt + φ) . ημθ) ]   =>

        V₀ .(ωL / Ζ)     =     V_0,πην  . ημθ     

        V₀ . (R / Ζ)    =       V_0,πην   . συνθ      =>     εφθ   =  ωL / R     

    ημθ = ωL  / [ (ωL)²  +  R²  ] ^1/2        συνθ  = R / [ (ωL)²  +  R²  ] ^1/2

 και       V² _0,πην  =   V²₀ .(ωL / Ζ)²  +    V²₀ . (R / Ζ)² =>   V² _0,πην =   V²₀ . [ (ωL)²  +  R²  ] / Ζ²      

υπάρχει περίπτωση    1/ωC  - ω.L ® 0  =>      ω² .L. C  ®  1  =>   ω  --->  1 / (L . C)^½  = ω₀  :   ιδιοσυχνότητα του κυκλώματος      τότε   Ζ²  =  ( ωL - 1/ωC )²  + R ²  ®   R ²                     

η μέγιστη τιμή του φορτίου  στον πυκνωτή  Q = V₀ / ω.C. Ζ   ®  V₀ / ω.C. R    όπως και το ρεύμα που διαρρέει το πηνίο  I  =   V0 .(ωL / Ζ)   =>   V0 .(ωL / R)  =  Ι₀     τότε   έχουμε συντονισμό   το πλάτος του ρεύματος γίνεται μέγιστο  

              για συχνότητες     ω  <  ω₀      έχουμε   Ι  <  Ι₀        και      για    ω  >  ω₀    έχουμε   Ι  <  Ι₀