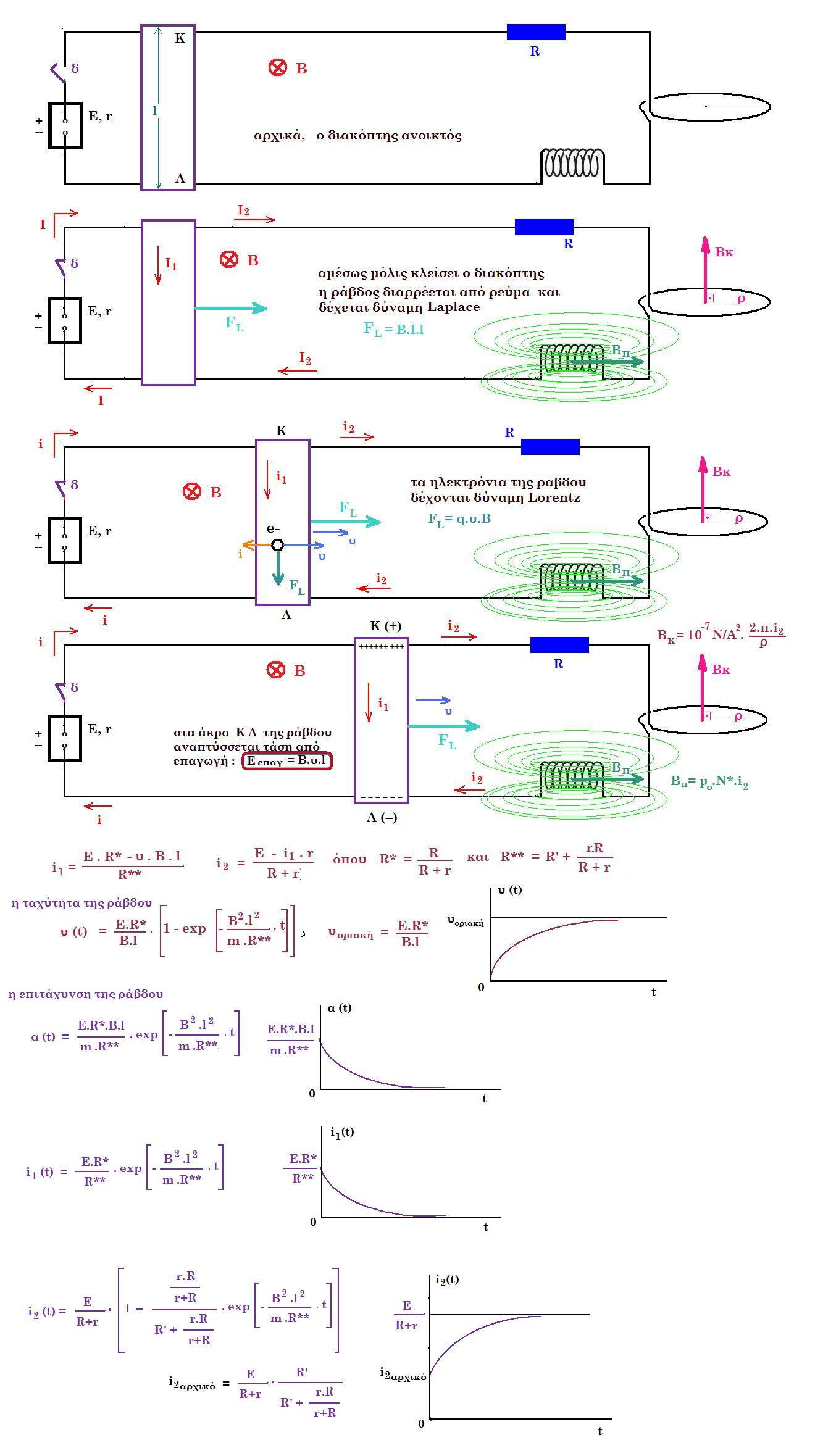
Η ράβδος έχει μάζα m , μήκος l ,     ωμική αντίσταση R',   το πηνίο έχει μηδενική ωμική αντίσταση

Ο διακόπτης ανοικτός  δεν κυκλοφορεί ρεύμα.

Μόλις κλείσουμε τον διακόπτη η ράβδος διαρρέεται από ρεύμα  και επειδή βρίσκεται μέσα σε μαγνητικό πεδίο  Β  δέχεται δύναμη  Laplace :  F_L  =  B . I₁ . l  Η ράβδος κινείται λόγω της δύναμης  με ταχύτητα  υ.   Τα ηλεκτρόνια της ράβδου λόγω της ταχύτητας μέσα στο μαγνητικό πεδίο  δέχονται δύναμη Lorentz  :  F_L  =  q_e . υ . Β   με συνέπεια να συσσωρεύονται στο ένα άκρο  ( Λ ) της ράβδου.  Έτσι το άκρο Λ  φορτίζεται αρνητικά  ενώ  το άκρο Κ  θετικά. Αναπτύσσεται τάση V_KΛ  στα άκρα της ράβδου λόγω επαγωγής,  δηλαδή ηλεκτρικό πεδίο με ένταση :  Ε = V_KΛ / l  τα ηλεκτρόνια δέχονται δύναμη από το ηλεκτρικό πεδίο :  FE  =  q_e . E  =  q_e .( V_KΛ / l )   η οποία έχει κατεύθυνση από το Λ  προς το Κ.   Η μαγνητική δύναμη Lorentz  και  η ηλεκτρική τοιαύτη είναι αντίθετες.   Με την πάροδο του χρόνου περισσότερα ηλεκτρόνια συσσωρεύονται στο άκρο Λ  οπότε  αυξάνεται η τάση V_KΛ    και το μέτρο της FE    κάποια στιγμή  :   F_L = F_Ε   =>  q_e . υ . Β  =  q_e .( V_KΛ / l )  =>    υ . Β  =   V_KΛ / l   =>   VKΛ  = υ . Β . l  =  Ε_{επαγωγική}   

η ράβδος διαρρέεται από ρεύμα  i₁  δέχεται δύναμη  Laplace : F_L  =  B . I₁ . l     (1)

κλειστό  κύκλωμα :   Ε  - Ε_επαγ  = i . r  +  i₁ . R'  =>   Ε  - υ . Β . l   = i . r  +  i₁ . R'   =>   Ε  - υ . Β . l   =  ( i₁ + i₂ ) . r  +  i₁ . R'   =>      Ε  - υ . Β . l   =   i₂ . r  +  i₁ . ( R' + r )    (2)          

  επίσης έχουμε :    E =  ( i₁ + i₂ ) . r  +  i₂ . R   =>    E =  i₁ . r  +  i₂ . (R + r)   =>    ( E  -  i₁ . r )  / (R + r)   =   i₂    (3)            

 (3) , (2)  =>   Ε  - υ . Β . l   =  ( E  -  i₁ . r ) . r  / (R + r)  +  i₁ . ( R' + r )    =>        Ε  - υ . Β . l   =    E. r  / (R + r)  -  i₁ . r² / (R + r)  +  i₁ . ( R' + r )    =>  

              =>    Ε  - υ . Β . l   =    E. r  / (R + r)   +  i₁ . [  R' + r  -  r² / (R + r)  ]    =>    Ε . R / (R + r)   - υ . Β . l   =   i₁ . [ R' + r  -  r² / (R + r) ]    (4)         i₁ =  {  Ε . R*  - υ . Β . l } / R**    όπου     R*  = R / (R + r)    και   R**  =   R' + r  -  r² / (R + r) =  R'  +  r.R /(R+r)            η  (1) γίνεται F_L  =  B .  l .  {  Ε . R*  - υ . Β . l } / R**  =   B.l.Ε.R* / R**    -  υ .Β² .l² / R**    

2ος  νόμος Νεύτωνα :   ΣF  =  m . α    =>     F_L  =  m . dυ/dt   =>      B.l.Ε.R* / R**    -  υ .Β² .l² / R**   =  m . dυ/dt    => - Β² .l² / m .R** . dt   =   d(-υ)  /  ( Ε.R* / Β.l   -  υ )  =>

 =>    ln { ( Ε.R* / Β.l  -  υ ) / ( Ε.R* / Β.l ) }   =   - Β² .l² / m .R** .  t  =>    Ε.R* / Β.l  -  υ   =   ( Ε.R* / Β.l ) . exp { - Β² .l²  / m .R** . t }   =>  

                                                                 =>          υ (t)   =   ( Ε.R* / Β.l ) . ( 1 - exp { - Β² .l² / m .R** . t } )       

η ράβδος αποκτά οριακή ταχύτητα :   υ_οριακή  =   Ε.R* / Β.l     δηλαδή   Ε_επαγ = Ε  τότε  διαρρέεται από ρεύμα : i₁ = 0     τότε  η (3) =>   i₂ =  E / (R+r)  τελική τιμή ρεύματος μετά από χρόνο

η επιτάχυνση της ράβδου :   α  =  dυ/dt   =>     α (t)  =  ( Ε.R* / Β.l ) .{ - Β² .l² / m .R** .  t } . (- exp { - Β² .l² / m .R** .  t } )        =>

                                                                 =>        α (t)  =   Ε.R*.Β.l  / m .R** . exp { - Β² .l² / m .R**. t }          μειώνεται εκθετικά με τον χρόνο        

το ρεύμα  που διαρρέει την ράβδο :     i₁ =  {  Ε . R*  - υ . Β . l } / R**  =>    i₁ (t)  =  ( Ε.R* / R**) . exp { - Β² .l² / m .R** . t }          

                           η σχέση  (3)  =>   i2 (t)  =  ( E  -  i₁ . r )  / (R + r)   =  Ε / (R + r) . [ 1  -  ( R*. r / R**) . exp { - Β² .l² / m .R** . t }  ]      

από τις σχέσεις :      Ε   =   i₂ . r  +  i₁ . ( R' + r )     και     E =  i₁ . r  +  i₂ . (R + r) 

    [ Ε   -  i₁ . ( R' + r ) ] /  r  =   i₂            E =  i₁ . r  +   [ Ε   -  i1 . ( R' + r ) ] . (R + r) /  r       =>     i₁ . [ R' + r  -  r² / (R + r) ]   =  Ε. R / (R + r)    =>    i₁ . R**   =  Ε. R*    =>    i₁  =  Ε. R* / R**    αρχική τιμή του ρεύματος που διαρρέει την ράβδο

από  :  Ε =  i₂ . r +  i₁ . (R' + r)   &   E =  i₁ . r  +  i₂ .(R + r)     αφαιρώντας κατά μέλη :   0   =   i₁ . R' -  i₂ .  R  =>    i₂  =  i₁ . R' / R  =  Ε. ( R* / R** ) . ( R' / R )  =>       i₂ =    E/(R+r) . R' / [ R' + r.R / (r+R) ]       αρχική τιμή του ρεύματος που διαρρέει το πηνίο  και την αντίσταση R