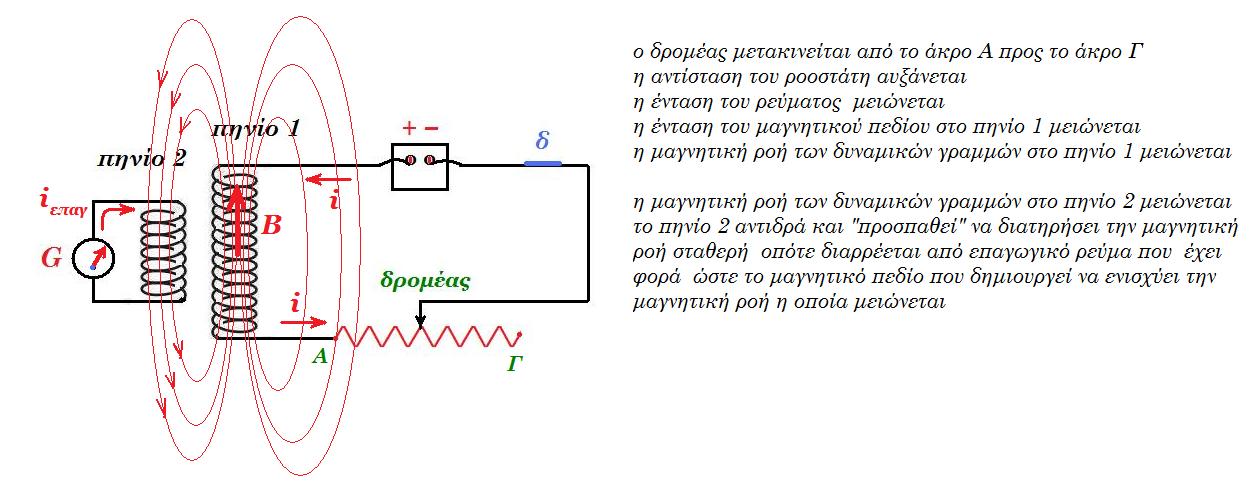
ο διακόπτης δ κλειστός το πηνίο Π1 διαρρέεται από ρεύμα i1 = Ε / (r + R1 + Rπ1)
το μαγνητικό πεδίο που δημιουργείται στο πηνίο Π1 έχει ένταση (στο κέντρο του) Β1 = μο . Ν1 . i1 / l1 ( l1 : μήκος πηνίου Π1 )
η μαγνητική ροή η οποία διέρχεται από τις σπείρες του πηνίου Π2 είναι : Φ = ½.Β1 .Α.Ν2 = ½.μο.Ν1 .Ν2 .Α/l1 .i1
Όταν ανοίγει ο διακόπτης δ μηδενίζεται το ρεύμα Ι1 μηδενίζεται το μαγνητικό πεδίο Β1 καθώς και η μαγνητική ροή Φ, σε χρόνο Δt.
Έχουμε μεταβολή ροής δυναμικών γραμμών μέσα από τις σπείρες του πηνίου Π2 : ΔΦ = Φτελική - Φαρχική = 0 - Φ = -Φ.
Στα άκρα του εμφανίζεται επαγωγική τάση Εεπαγ = - ΔΦ / Δt = - ½.μο. Ν1.Ν2.Α/l1 . Δi1 / Δt
μο.Ν1.Ν2.Α/l1 = Μ1,2 συντελεστής αμοιβαίας επαγωγής μεταξύ των πηνίων Π1 και Π2 , έχει μονάδα μετρήσεως το 1 Henry ( 1 H = 1 N.m/A2 )
π ρ ό β λ η μ α
Δεδομένα : R1 = 10 Ω, R2 = 20 Ω, πολική τάση πηγής V = 20 Volt,
τα πηνία έχουν μήκος l1 = l2 = 10 cm , αριθμό σπειρών : Ν1 = Ν2 = 100 σπείρες και μηδενική ωμική αντίσταση,
το εμβαδόν επιφάνειας κάθε σπείρας : A = 20 cm2 , ο χρόνος Δt = 10-4 sec, kμαγν = 10-7 N/A2.
Ζητούμενα : α) ένταση μαγνητικού πεδίου Β1 , β) επαγωγική τάση, γ) επαγωγικό ρεύμα, δ) φορτίο ΔQ,
ε) συντελεστής αμοιβαίας επαγωγής των πηνίων, στ) συντελεστής αυτεπαγωγής του πηνίου Π1
....................................................................................................................................................................................
i1 = V / R1 = 20 V / 10 Ω => i1 = 2 Α, Β1 = 10-7 Ν/Α2 . Ν1 . i1 / l1 = 10-7 N/A2 . 100 . 2 A / 10-1 m => B1 = 2.10-4 Tesla,
Φ = ½ . Β1 . Α . Ν2 = ½ . 2 . 10-4 Τesla . 20 . 10-4 m2 . 100 = 2 . 10-5 Weber, ΔΦ = - Φ = - 2.10-5 Weber,
Εεπαγ = - ΔΦ / Δt = - ( - 2.10-5 Weber ) / 10-4 sec => Εεπαγ = 0,2 Volt, Ιεπαγ = Εεπαγ / R2 = 0,2 Volt / 20 Ohm => Ιεπαγ = 0,01 A,
ΔQ = Ιεπαγ . Δt = 0,01 A . 10-4 sec => ΔQ = 10-6 Coulomb = 1 μC.
συντελεστής αμοιβαίας επαγωγής : Μ1,2 = μο .Ν1 .Ν2 .Α / l1 = 4.π.10-7 Ν/Α2 . 100 . 100 . 20.10-4 m2 / 0,1 m = 8.π.10-5 Ν.m/A2 => Μ1,2 = 8.π.10-5 Henry
συντελεστής αυτεπαγωγής του πηνίου Π1 : L1 = μο . Ν12 . Α / l1 = 4.π.10-7 Ν/Α2 . 1002 . 20.10-4 m2 / 0,1 m => L1 = 8.π.10-5 Henry
τ = L1 / R1 = 8.π.10-5 Η / 20 Ω 4.π.10-6 sec σε χρόνο περίπου : 5.τ = 20.π.10-6 sec = 6,28.10-5 sec μηδενίζεται το μαγνητικό πεδίο στο πηνίο Π1
...........................................................................................................................
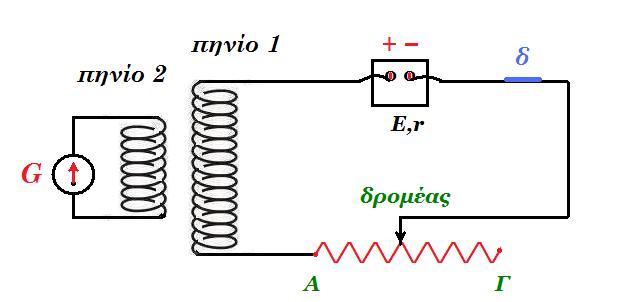Το πηνίο 1 έχει Ν1 = 100 σπείρες, μήκος l1 = 0,1 m, ωμική αντίσταση Rπ,1 = 8 Ω, κάθε σπείρα έχει εμβαδόν επιφάνειας Α = 10-3 m2 ενώ το πηνίο 2 έχει Ν2 = 10 σπείρες, μήκος l2 = 0,1 m, ωμική αντίσταση Rπ,2 = 5 Ω, και κάθε σπείρα έχει εμβαδόν επιφάνειας Α = 10-3 m2. Η πηγή συνεχούς ρεύματος έχει ηλεκτρεγερτική δύναμη Ε = 12V και εσωτερική αντίσταση r = 2 Ω. Ο ροοστάτης (μεταβλητή αντίσταση) έχει ελάχιστη αντίσταση Rελαχ. = 10 Ω όταν είναι στην θέση Α και μέγιστη Rμέγ. = 90 Ω όταν είναι στην θέση Γ. Μετακινούμε τον δρομέα από την θέση Α προς την θέση Γ σε χρονικό διάστημα Δt = 0,01 sec.
έχουμε μεταβολή στην ένταση του ρεύματος το οποίο διαρρέει το πηνίο 1, Δi = iτελ - iαρχ
iαρχ = Ε / ( r + Rπ,1 + Rελαχ. ) = 12 / ( 2 + 8 + 10 ) = 0,6 A
iτελ = Ε / ( r + Rπ,1 + Rμέγ. ) = 12 / ( 2 + 8 + 90 ) = 0,12 A
τότε Δi = iτελ - iαρχ = 0,12 - 0,6 = - 0,48 Α
έτσι έχουμε μεταβολή της έντασης του μαγνητικού πεδίου που δημιουργείται στο πηνίο 1
ΔΒ = Βτελ - Βαρχ = 4π 10-7 Ν1 iτελ / l1 - 4π 10-7 Ν1 iαρχ / l1 = 4π 10-7 Ν1 Δi / l1 =
= 4π 10-7 100 (-0,48) / 0,1 = - 192π 10-4 Τ
έχουμε μεταβολή μαγνητικής ροής ΔΦ = ΔΒ Α = - 192π 10-4 Τ 10-3 m2 = - 192π 10-7 Wb
επειδή τα πηνία είναι πολύ κοντά μεταξύ τους η μεταβολή μαγνητικής ροής στο πηνίο 1 επηρεάζει το πηνίο 2 οπότε αναπτύσσεται επαγωγική τάση στα άκρα του πηνίου 2
Εεπαγ = - ΔΦ/Δt = - (- 192π 10-7 Wb) / 0,01 s = 192π 10-5 Volt @ 0,006 Volt = 6 mV
θα κυκλοφορήσει επαγωγικό ρεύμα εντάσεως iεπαγ = Eεπαγ / Rπ,2 = 6 mVolt / 5 Ω = 1,2 mA για χρονικό διάστημα Δt = 0,01 sec
οπότε διέρχεται φορτίο από το γαλβανόμετρο q = iεπαγ Δt = 1,2 mA 0,01 s = 12 μC
ΔΦ / Rπ,2 = 192π 10-7 Wb / 5 Ω = 6 10-5 / 5 = 1,2 10-5 = 12 μC = q
