AΣΚΗΣΗ 1.
Μεταλλικό συρμάτινο πλαίσιο ωμικής αντίστασης Rσ = 20 Ω φέρει Ν = 10 περιελίξεις που κάθε μία έχει εμβαδόν επιφάνειας Α = 0,01 m2 , στρέφεται περί άξονα μέσα σε ομογενές μαγνητικό πεδίο εντάσεως Β = 0,2 Τ με σταθερή συχνότητα f = 10 Hz. Τα άκρα του πλαισίου συνδέονται με κυκλικό αγωγό ακτίνας ρ = 0,5 m μηδενικής ωμικής αντίστασης και λαμπτήρα σε σειρά ωμικής αντίστασης Rλ = 30 Ω.
η γωνιακή ταχύτητα του πλαισίου είναι : ω = 2 π f => ω = 2 π 10 Hz => ω = 20 π rad/sec
ο χρόνος Τ για μία περιστροφή του πλαισίου είναι : Τ = 1/f => Τ = 1/10 Hz => Τ = 0,1 sec
στα άκρα του πλαισίου εμφανίζεται επαγωγική τάση μεταβαλλόμενης τιμής ως προς τον χρόνο, με μέγιστη τιμή : V0 = ω . N . B . A =>
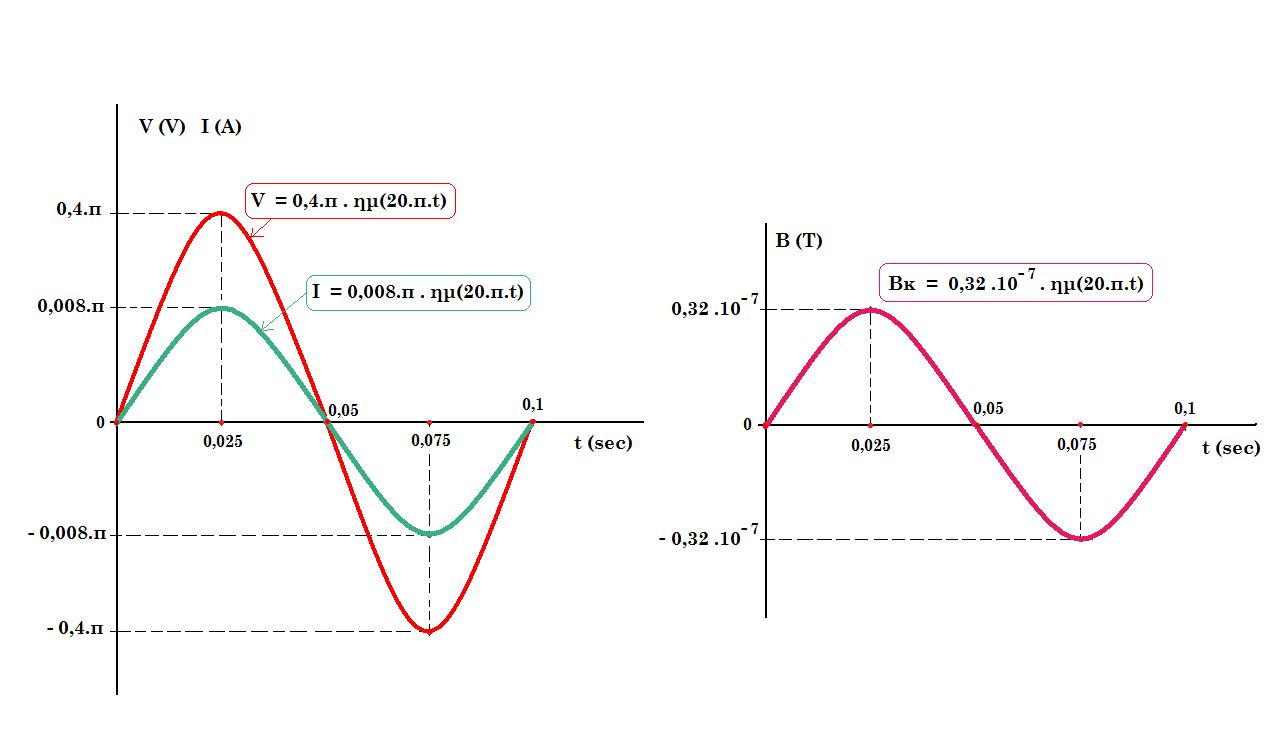
=> V0 = 20.π rad/sec . 10 . 0,2 Τ . 0,01 m2 => V0 = 0,4.π Volt
η συνολική αντίσταση του κυκλώματος είναι : Rολ = Rλ + Rσ = 20 Ω + 30 Ω => Rολ = 50 Ω
η μέγιστη τιμή της έντασης του ρεύματος που διαρρέει το κύκλωμα είναι : Ι0 = V0 /Rολ = 0,4.π V/50 Ω => Ι0 = 0,008.π Α
η εξίσωση της εναλλασσόμενης τάσης ως προς τον χρόνο είναι :
V(t) = V0 ημωt => V(t) = 0,4.π ημ(20.π.t)
η εξίσωση της έντασης του εναλλασσομένου ρεύματος ως προς τον χρόνο είναι :
Ι(t) = Ι0 ημ(ω.t) => Ι(t) = 0,008.π ημ(20.π.t)
το ρεύμα διαρρέει τον κυκλικό αγωγό, δημιουργείται μαγνητικό πεδίο του οποίου η ένταση στο κέντρο του κύκλου είναι : Βκ = 10-7 Ν/Α2 . 2.π.Ι / ρ =>
=> Βκ = 10-7 Ν/Α2 . 2.π.0,008.π . ημ(20.π.t) / 0,5 m =>
=> Βκ = 10-7 Ν/Α2 . 2.π.0,008.π / 0,5 m . ημ(20.π.t) =>
=> Βκ = 10-7 . 2.π2 .0,008 / 0,5 . ημ(20.π.t) =>
=> Βκ = 10-7 . 4.π2 .0,008 . ημ(20.π.t) =>
=> Βκ = 10-7 . π2 .0,032 . ημ(20.π.t) =>
=> Βκ = 0,32 .10-7 . ημ(20.π.t) παρατηρούμε ότι η ένταση του μαγνητικού πεδίου είναι αρμονικά μεταβαλλόμενη ως προς τον χρόνο με κυκλική συχνότητα : ω = 20.π rad/sec και παρουσιάζει μέγιστη τιμή : Βκ,0 = 0,32 . 10-7 Τesla

AΣΚΗΣΗ 2.
 bbbb
bbbb