ΘΕΜΑ Α

Α1.  Δύο συρμάτινα πλαίσια έχουν ίσα εμβαδά και περιστρέφονται με την ίδια γωνιακή ταχύτητα ω  μέσα σε ομογενές μαγνητικό πεδίο.  Αν 𝛮₁ και 𝛮₂ ο αριθμός σπειρών για κάθε πλαίσιο, ο λόγος  𝑉_εν1 / 𝑉_𝜀ν2  των ενεργών τιμών των εναλλασσόμενων τάσεων στα άκρα κάθε πλαισίου είναι:
α. 𝛮₁/𝛮₂
β. 𝛮₂/𝛮₁
γ. (𝛮₁/𝛮₂)²
δ. (𝛮₂/𝛮₁)²

Α2.  Αν το πλάτος της έντασης του εναλλασσόμενου ρεύματος που διαρρέει έναν αντιστάτη διπλασιαστεί, τότε η μέση ισχύς που καταναλώνεται στον αντιστάτη:
α. θα διπλασιαστεί.
β. θα υποδιπλασιαστεί.
γ. θα παραμείνει η ίδια.
δ. θα τετραπλασιαστεί.

Α3.  Στα άκρα αντιστάτη αντίστασης 𝑅 εφαρμόζουμε εναλλασσόμενη τάση της μορφής  𝑣 = 𝑉.ημωt. Η ένταση του ρεύματος που διαρρέει τον αντιστάτη:
α. έχει διπλάσια συχνότητα από τη συχνότητα της τάσης.
β. έχει την ίδια φάση με την τάση.
γ. δίνεται από την εξίσωση  𝑖 = 𝐼.ημ(𝜔𝑡 + 𝜋/2).
δ. έχει ενεργό τιμή 𝐼_𝜀ν = 𝛪/2.

Α4.  Μία συνεχής τάση 𝑉_𝛴  και μια ημιτονοειδής εναλλασσόμενη τάση με ενεργό τιμή 𝑉_𝜀ν  προκαλούν τα ίδια θερμικά αποτελέσματα, στον ίδιο χρόνο, σε αντιστάσεις 𝑅 και 4𝑅. Ο λόγος 𝑉_𝜀ν / 𝑉_𝛴   είναι ίσος με:         α. 1       β. 2            γ. 1/2             δ. 4

Α5.   Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές ή λανθασμένες.
Η εναλλασσόμενη τάση που δημιουργείται με περιστρεφόμενο πλαίσιο σε ομογενές μαγνητικό πεδίο είναι της μορφής :  V(t) = 220√2.ημ100𝜋𝑡   (SI)   και εφαρμόζεται στα άκρα αντιστάτη με αντίσταση 𝑅 = 22 Ω.
α.  Η ενεργός ένταση του ρεύματος που διαρρέει τον αντιστάτη είναι 10 A.
β.  Η στιγμιαία τιμή της έντασης γίνεται μέγιστη τη χρονική στιγμή 𝑡₁ = 5 ms.
γ.  Από τη χρονική στιγμή 𝑡₁ = 5 ms  έως τη χρονική στιγμή 𝑡₂ = 10 ms, η φάση της τάσης αυξάνεται κατά  Δφ = 𝜋/2.
δ.  Ο μέγιστος ρυθμός παραγωγής θερμότητας στον αντιστάτη είναι 1100 J/s.
ε.  Τη χρονική στιγμή 𝑡₂  η στιγμιαία ισχύς στον αντιστάτη είναι μηδέν.
ζ.  Αν διπλασιάσουμε την ένταση του μαγνητικού πεδίου, θα υποδιπλασιαστεί η ενεργός ένταση του ρεύματος που διαρρέει τον αντιστάτη.

α.  i = V / R  =>  i = 220√2 / 22 ημ100𝜋𝑡  =>  i(t) = 10√2 ημ100𝜋𝑡  (SI)        i_εν = Ι / √2  =>  i_εν = 10 Α    (Σ)

β. i(0,005) = 10√2 ημ(100𝜋 0,005)  =  10√2 ημ(𝜋/2)  = 10√2 A  μέγιστη τιμή της έντασης του ρεύματος    (Σ)

γ.  f =  100𝜋 / 2𝜋  =>  f = 50 Hz     T = 1 / f  = 0,02 sec = 20 ms ,    τη στιγμή  t₁ = T/4   η ένταση του ρεύματος γίνεται μέγιστη  όπως  και η τάση,   τη στιγμή  t₂ = T/2  η τάση μηδενίζεται  όπως  και  η ένταση του ρεύματος,   η φάση της τάσης  από  100π.0,005 rad = π/2 rad   γίνεται  10π.0,010 rad = π rad    δηλαδή  αυξάνεται κατά  π/2 rad      (Σ)

δ.  P_max = V I =  220√2  10 √2   =  4400 Watt      (Λ)

ε.  τη χρονική στιγμή 𝑡₂ = 10 ms   η στιγμιαία τιμή της τάσης  είναι  μηδέν  όπως  και της έντασης του ρεύματος    συνεπώς  η στιγμιαία ισχύς στον αντιστάτη είναι μηδέν         (Σ)

ζ.  αν διπλασιάσουμε την ένταση του μαγνητικού πεδίου  θα  διπλασιασθεί  το πλάτος της εναλλασσόμενης τάσης  καθώς και της έντασης του ρεύματος   άρα  η ενεργός ένταση θα διπλασιασθεί           (Λ)

ΘΕΜΑ Β 

Β1.   Γεννήτρια εναλλασσομένου ρεύματος, η οποία περιστρέφεται με συχνότητα f=50Ηz, τροφοδοτεί αντίσταση 𝑅   η οποία διαρρέεται από εναλλασσόμενο ρεύμα με ενεργό ένταση 𝐼_𝜀ν=4Α.   Αν διπλασιαστεί η συχνότητα περιστροφής, το πλάτος της έντασης του ρεύματος που θα διαρρέει την αντίσταση είναι:
         α.  𝐼 = 4√2 Α                 β.  𝐼 = 8√2 Α                γ.  𝐼 = 8 Α
Να επιλέξετε τη σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.

αν διπλασιασθεί η συχνότητα περιστροφής,  θα διπλασιασθεί  το πλάτος τηε εναλλασσόμενης τάσης οπότε  η μέγιστη τιμή της έντασης του ρεύματος  άρα  και η ενεργός ένταση : Ι_εν = 8 Α => Ι = 8√2 Α 

Β2.  Σε ένα σύρμα διαβιβάζουμε ταυτόχρονα δύο εναλλασσόμενα ρεύματα με εξισώσεις  𝑖₁ = 𝑖₂ = Ι.ημω𝑡. Η ενεργός ένταση του ρεύματος που διαρρέει το σύρμα είναι
α. 𝛪√2
β. 2𝛪√2
γ. 𝛪/√2
Να επιλέξετε τη σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.

το συνολικό ρεύμα είναι  2. Ι.ημω𝑡   οπότε   Ι_εν = 2.Ι / √2 = Ι√2

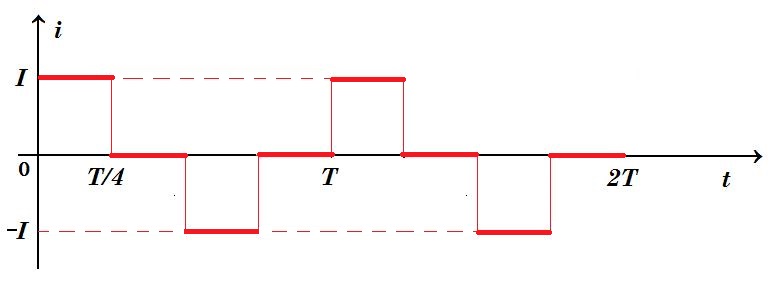
Β3.   Το εναλλασσόμενο ρεύμα που παριστάνεται στο διάγραμμα του σχήματος έχει την ίδια ενεργό τιμή με ένα ημιτονοειδές ρεύμα της μορφής:
α.  𝑖 = 2Ι ημ(2𝜋𝑡/𝑇)
β.  𝑖 = √2Ι ημ(2𝜋𝑡/𝑇)
γ.  𝑖 = Ι ημ(2𝜋𝑡/𝑇)

Να επιλέξετε τη σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.

(α)    Ι_εν = 2Ι/ √2 = I √2                 (b)    Ι_εν = √2Ι / √2 = I                   (γ)    Ι_εν = Ι / √2      

 Q_θερμ = Ι² R T/4  +  0  +  Ι² R T/4  +  0  =  2 Ι² R T/4  = Ι²/2 R T  οπότε  Ι_εν = Ι / √2

ΘΕΜΑ Γ

Μια αντίσταση 𝑅 = 20 Ω  διαρρέεται από εναλλασσόμενο ρεύμα με χρονική εξίσωση 𝑖(t)=Ι.ημ100𝜋𝑡 (SI).   Κάποια χρονική στιγμή  𝑡₁   που η φάση του ρεύματος είναι 𝜑₁ = 𝜋/4 rad,  η στιγμιαία τιμή της έντασης του ρεύματος είναι 𝑖 = √2 Α.
α.  Ποια είναι η στιγμιαία τιμή της τάσης τη χρονική στιγμή 𝑡₁;
β.  Μετά από πόσο χρόνο 𝛥𝑡, από τη χρονική στιγμή 𝑡₁, η φάση θα γίνει 3𝜑₁;
γ.  Βρείτε την ενεργό τιμή της τάσης στα άκρα του αντιστάτη.
δ.  Βρείτε τη μέγιστη ισχύ που μεταφέρεται από το ρεύμα στην αντίσταση.
Απ.[α. 𝑣 = 20√2 V,      β. 𝛥𝑡 = 1⁄200 s,       γ. 𝑉_𝜀ν = 20√2 V,        δ. p_max = 80 W]

    ω = 100π rad/s   =>    f  = 100π / 2π  =  50 Hz    =>    T  =  1 / f  =>    T  =  0,02 sec    

    i  = √2 A  =  I ημ(𝜋/4)  =>  √2  =  I √2 / 2  =>  I   =  2 A         V  =  I R  =>   V  =  40 Volt      

   v  =  V ημ(𝜋/4)  =   40 √2 / 2  =>    v  =  20√2 Volt      

   Δφ  =  3π/4  -  π/4  =  π/2    άρα    Δt  =  T / 4  =  0,02 / 4  =  0,005 sec

   V_εν  =  V / √2   =   40 / √2   =>   V_εν  =  20√2 Volt

    P_max  =  V I  =  40 V  2 A  =>   P_max  =  80 Watt     

ΘΕΜΑ Δ

Ένα ημιτονοειδές ρεύμα έχει εξίσωση  i = Ι.ημω𝑡   διαρρέει αντιστάτη με αντίσταση  R = 5 Ω. Τη χρονική στιγμή  t₁ = 5 ms έχει μέγιστη ένταση και τη χρονική στιγμή  t₂ = 15 ms παίρνει για πρώτη φορά την τιμή   i = −20√2 Α.
α.  Ποια η ενεργός ένταση του ρεύματος;
β.  Βρείτε τη συχνότητα και την περίοδο του ρεύματος.
γ.  Βρείτε τη μεταβολή της φάσης από τη στιγμή  t₁   έως τη χρονική στιγμή  t₂.
δ.  Κάντε τη γραφική παράσταση της έντασης του ρεύματος έως τη χρονική στιγμή που μηδενίζεται για τρίτη φορά.
ε.  Βρείτε το ρυθμό παραγωγής θερμότητας όταν η φάση της τάσης στα άκρα του αντιστάτη είναι 3π/2.

  t₁  =  T / 4  =  5 ms  =>   T = 20 ms           f  = 1 / T  =  50 Hz          ω = 2πf  =  100π rad/s      

  i = Ι.ημω𝑡  =>  −20√2  =  Ι.ημ(100π.0,015)  =  I .ημ(3π/2)  =>  I  = 20√2 A            I_εν  =  20 Α            

   Δφ  =  ω.( t₂ - t₁ ) = 100 π rad/s . 10 ms  = π rad  

 P =  i² R  =  I² ημ²ω𝑡  R  =  (20√2)² .ημ²(3π/2) .5  = 400 .2 .(-1)² .5  = 4000 Watt = 4000 J/s 

Ηλεκτρική συσκευή έχει ωμική αντίσταση  R,  διαρρέεται από συνεχές ρεύμα με ένταση  Ι₁   αλλά και εναλλασσόμενο με ένταση  Ι₂ = Ι₀₂ ημ(ωt + φ)    Να εκφράσετε το συνολικό ρεύμα συναρτήσει του χρόνου,  όπως επίσης την στιγμιαία ισχύ που καταναλώνεται στη συσκευή.

   I  =  I₁  +  I₀₂ ημ(ωt +φ)            η μέγιστη τιμή της έντασης είναι :  Ι₁ + Ι₀₂   και η ελάχιστη :    Ι₁ - Ι₀₂   

  P  =  ( I₁  +  I₀₂ ημ(ωt +φ) )²  R   

Ηλεκτρική θερμάστρα έχει ωμική αντίσταση  R = 100 Ω   και  διαρρέεται από συνεχές ρεύμα με ένταση  Ι₁ = 2 Α  αλλά και εναλλασσόμενο με ένταση  Ι₂ = 2.ημ100πt    Να γίνει το διάγραμμα του συνολικού ρεύματος συναρτήσει του χρόνου,    να υπολογισθεί η μέση ισχύς που καταναλώνει η θερμάστρα,     να βρεθεί η στιγμιαία ισχύς που καταναλώνει η θερμάστρα τις χρονικές στιγμές  t₁ = 15 msec,   t₂ = 25 msec     t₃ = 40 msec     t₄ = 42,5 msec

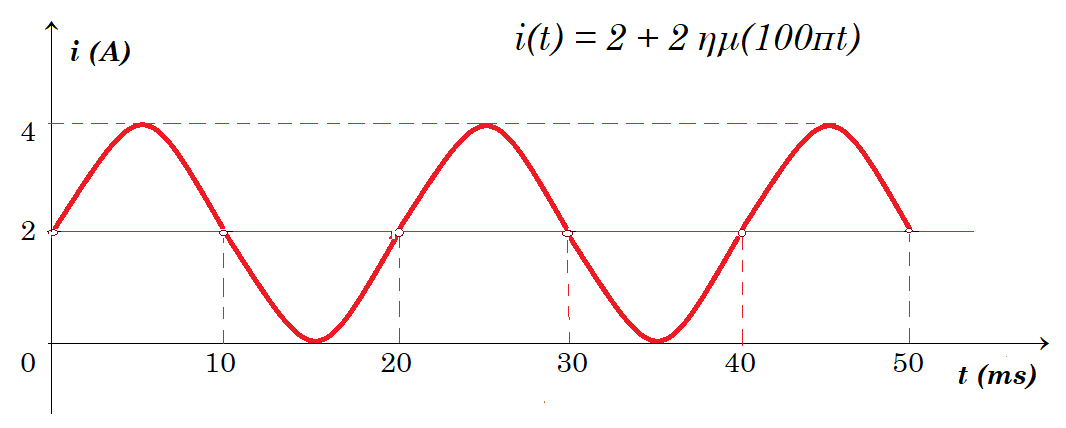
  I  =  I₁  +  I₂  =  2  +  2 ημ(100πt)     μέγιστη ένταση ρεύματος  Ι_μεγ. = 4 Α    ελάχιστη τιμή  Ι_ελαχ. = 0

t₁ = 15 ms     I = 2 + 2 ημ(100π 0,015)  = 2 + 2 ημ(3π/2) =  2 + (- 2) = 0         P = 0

t₂ = 25 ms     I = 2 + 2 ημ(100π 0,025)  = 2 + 2 ημ(5π/2) =  2 + 2 = 4 A          P = I² R = 4² 100 = 1600 Watt

t₃ = 40 ms     I = 2 + 2 ημ(100π 0,04)  = 2 + 2 ημ(4π) =  2 A                           P = I² R = 2² 100 = 400 Watt

t₄ = 42,5 ms  I = 2 + 2 ημ(100π 0,0425)  = 2 + 2 ημ(4π + π/4) =  2 + 2 ημ(π/4) =  2 +  2 √2/2 =  ( 2 + √2 ) Α

                                                      P = I² R =  ( 2 + √2 )² 100 = ( 4 + 4√2 + 2 ) 100  =   ( 600 + 400√2 ) Watt

 P = I² R =  [ 2  +  2 ημ(100πt) ]² 100  =  400  +  800 ημ(100πt)  +  400 ημ²(100πt)  =

    =  400  +  800 ημ(100πt)  +  400 ½ ( 1 - συν(200πt) )  =  400  +  800 ημ(100πt)  +  200 ( 1 - συν(200πt) ) =

    =  600  +  800 ημ(100πt)  -  200 συν(200πt)   

             dW = P dt  =>  W  =  S_0®Τ  { 600  +  800 ημ(100πt)  -  200 συν(200πt) } dt =  600 Τ  +  0  -  0      

                        η μέση ισχύς που καταναλώνει η θερμάστρα είναι  600 Watt

  συν2α = συν²α - ημ²α  =  1  -  2 ημ²α  =>  ημ²α = ½ ( 1 - συν2α )  

Ηλεκτρικός λαμπτήρας πυρακτώσεως έχει ωμική αντίσταση  R,  διαρρέεται από εναλλασσόμενα ρεύματα με εντάσεις :  Ι₁ = Ι₀₁ .ημωt   &  Ι₂ = Ι₀₂ .ημ(ωt + φ)   Να εκφράσετε το συνολικό ρεύμα συναρτήσει του χρόνου,  όπως επίσης την στιγμιαία ισχύ που καταναλώνεται στον λαμπτήρα.

  I  =  I₁  +  I₂  =  Ι₀₁ ημ(ωt)   +  Ι₀₂ ημ(ωt + φ)  =  Ι₀₁ ημ(ωt)   +  Ι₀₂ ημ(ωt) συνφ   +  Ι₀₂ συν(ωt) ημφ  

  Ι₀²  =  Ι₀₁²  +  Ι₀₂²  +  2 Ι₀₁ Ι₀₂ συνφ       πλάτος συνολικού εναλλασσομένου ρεύματος

  εφθ  = Ι₀₂ ημφ / [ Ι₀₁ +  Ι₀₂ συνφ ]                

    I  =  I₀ ημ(ωt + θ)         στιγμιαία ένταση συνολικού εναλλασσομένου ρεύματος

   P  =  I² R  =  R I₀² ημ²(ωt + θ)      στιγμιαία ισχύς